基于直觉模糊相似度的刑侦血迹图像分割算法
兰 蓉,程阳子
(1.西安邮电大学通信与信息工程学院,陕西西安710121;
2.电子信息现场勘验应用技术公安部重点实验室,陕西西安710121;3.陕西省无线通信与信息处理技术国际合作研究中心,陕西西安710121)
随着刑事案件的发生,刑侦过程中会产生大量以图像为载体的证据资料。借助计算机进行刑侦图像的有效分割[1],可提高查找罪证的准确率,从而为刑侦串并案及后期数据归档所用[2]。血迹作为犯罪现场的重要证据之一,其形态特征、分布方式是案发过程的一种客观反映,血迹研究对判断案件性质、完成现场重建、刻画嫌疑对象有重要意义[3]。
受现场条件、复杂噪声等的影响,一般的刑侦现勘血迹图像在获取与存储时带有较强的不确定性,这使得血迹图像分割成为极具挑战性的研究内容。作为处理模糊、不精确信息的有力工具,直觉模糊集理论[4]能实现对刑侦血迹图像的不精确、不确定性的刻画。目前,直觉模糊集理论的研究已逐渐应用到图像阈值算法,如使用含参数的模糊隶属度生成直觉模糊集,以鉴别信息构造的对称直觉模糊交叉熵阈值算法[5];或者利用Sugeno直觉模糊模型生成含参数的直觉模糊集,以欧氏距离定义的直觉模糊散度阈值算法和指数型直觉模糊散度的阈值算法[6-7]。
已有的直觉模糊集构造方法中,模糊隶属度均存在参数。考虑到刑侦血迹图像形态多样、受外界干扰的影响,本文尝试采用基于直觉模糊集相似度量的阈值化[8-9]算法进行刑侦血迹图像分割,采用双边滤波对图像去噪,结合“投票模型”提出一种直觉模糊集的构造方法,并将其应用于血迹图像,从分割效果、量化指标两方面验证算法性能。
1 相关概念
1.1 模糊集
定义1[10]设X为论域,则X上的模糊集A可表示为
A={(x,μA(x)):x∈X},
其中,映射 μA:X→[0,1]称为模糊集 A的隶属度函数。
1.2 直觉模糊集
定义2[4,11]设X为论域,则 X上的直觉模糊集珘A可表示为
珘A={(x,μ珘A(x),ν珘A(x)):x∈X},
其中,映射 μ珘A(x):X→[0,1],映射 ν珘A(x):X→[0,1]分别称为直觉模糊集珘A的隶属度函数和非隶属度函数,且满足 0≤μ珘A(x)+ν珘A(x)≤1(x∈X),则π珘A(x)=1-μ珘A(x)-ν珘A(x)为 珘A 中元素 x 的犹豫度。令 IFSs(X)表示X上的所有直觉模糊集之集。
2 血迹图像的直觉模糊相似度阈值分割
血迹是刑侦案发现场常见的一类痕迹,血迹图像也是一种最常见的刑侦图像。根据形成机理,血迹类型可分为溅落状、渗透状、流柱状、滴落状、抛甩状等[12]。这类痕迹常处于复杂的环境下,呈现出边缘形态上的任意性和颜色渐变性。因此,为了后续精确提取目标,有必要通过滤波[13]降低周围干扰的影响。双边滤波[14]对邻域内各像素的空间距离及灰度相似性进行非线性组合,可达到抑制噪声,同时较好地保持血迹边缘和细节的效果。此外,血迹图像自身具有较强的模糊性和不确定性,因此,结合双边滤波,以直觉模糊集为理论依据进行血迹图像阈值分割具有一定的合理性。
2.1 图像双边滤波
对任意图像f,双边滤波后像素点(i,j)处的灰度值为

其中,Sx,y表示像素点(i,j) 的(2r+1) × (2r+1) 邻域,r为滤波半径;w(i,j)表示 Sx,y邻域内各像素点的权重,即

其中
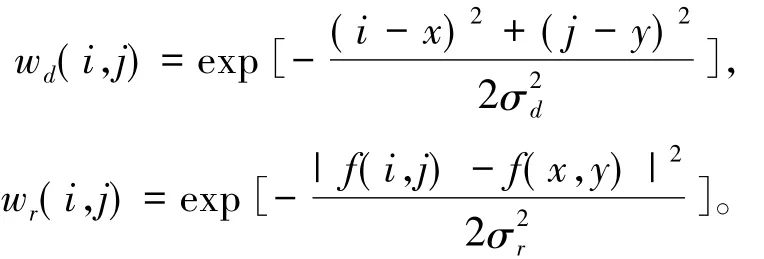
σd和σr分别表示空间域、值域的标准差;f(i,j)和f(x,y) 分别表示像素点(i,j)、(x,y) 处的灰度值。
2.2 基于投票模型生成直觉模糊集
目前,构造图像直觉模糊集模型的方法大多以图像的模糊隶属度为基础,利用含有参数的函数将一个模糊集转化为直觉模糊集。然而,参数的确定不但耗费大量时间,而且影响图像分割效果。为了有效避免参数选取问题,降低时间成本,借助“投票模型”[15]获得图像的直觉模糊集模型。
对论域X上的模糊集
A={(x,μA(x)):x∈ X},
μA(x)表示隶属度,可理解为支持的程度,则1-μA(x)表示非隶属度,即反对的程度。在实际表决中,尽管支持和反对者持有不同观点,但这些观点在传播的过程中总会互相影响。一方面,赞成者的观点会影响反对者,即 μA(x)[1-μA(x)];同时,反对者的观点也会影响赞成者,即[1-μA(x)]μA(x)。这种相互影响表现出一定的犹豫,即2μA(x)[1-μA(x)]。因此,基于“投票模型”可以生成直觉模糊集 珘A,其隶属度 μ珘A(x)、非隶属度ν珘A(x) 及犹豫度π珘A(x) 分别为
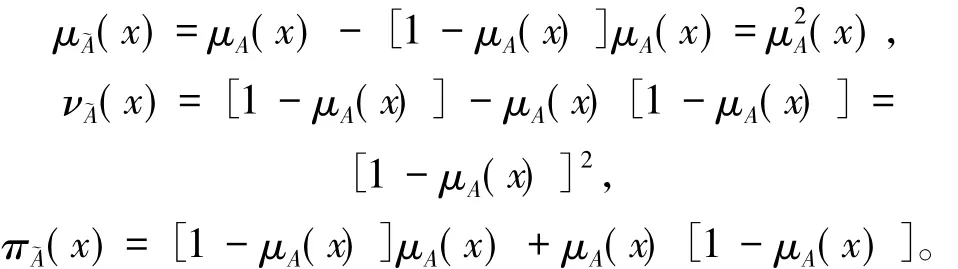
则论域X上的直觉模糊集珘A为
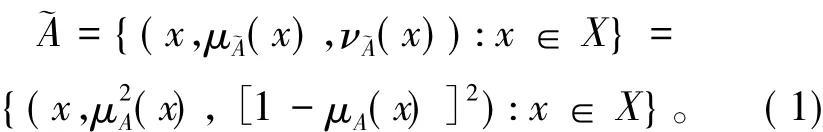
设一幅M×N的图像I可表示为一个模糊集,分割阈值为 T,灰度值 g的取值范围为 0,1,…,L - 1,即
I={(g,μI(g,T)):g ∈ {0,1,…,L - 1}}。
根据式(1)得到其直觉模糊集表示
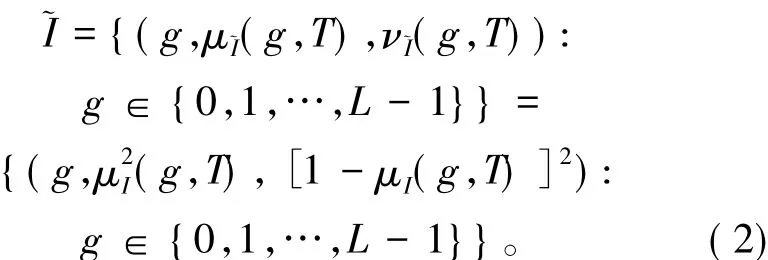
2.3 基于直觉模糊集相似度的阈值分割算法
本文提出的阈值化分割算法采用Vague集(与直觉模糊集在数学上等价[16])上的相似度为目标函数优化阈值,定义如下。
定义3[17]设X为有限论域,则直觉模糊集珘A,珘B∈IFSs(X)之间的相似度为
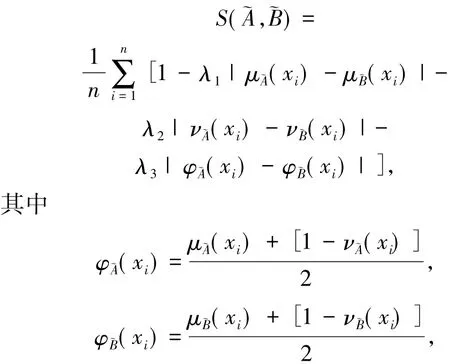
权重参数满足
λ1≥ 0,λ2≥0,λ3≥ 0,λ1+ λ2+ λ3=1
且λ1、λ2、λ3中至少有两个不同时为0的要求。
以定义3中最大相似度为优化准则,本文给出基于直觉模糊相似度的血迹图像阈值分割算法,具体步骤如下。
步骤1 采用限制等价函数[18](Restricted E-quivalence Function,REF)3型建立图像的模糊集μI(g,T),即 μI(g,T)= μREF3I(g,T)。
步骤2 根据式(2)得到图像的直觉模糊集表示。
步骤3 计算图像I与理想分割图像B的直觉模糊相似度S(珓I,珘B;T),取相似度最大时的T值为最佳分割阈值。
对理想分割图像B,有μ珘B(g)=1,ν珘B(g)=0,g∈{0,1,…,L - 1}。因此,相似度可简化为
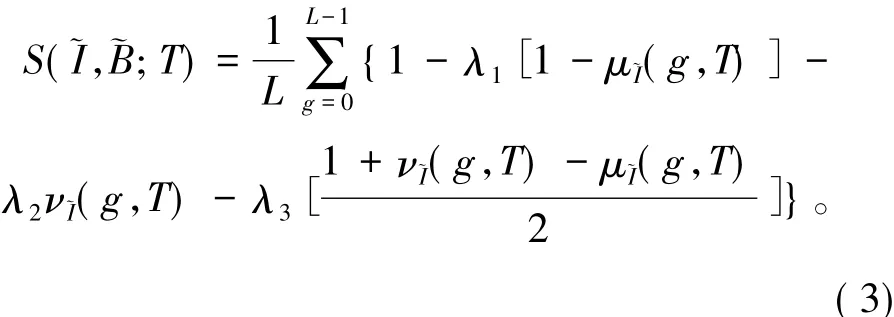
则选取最佳阈值的目标函数为
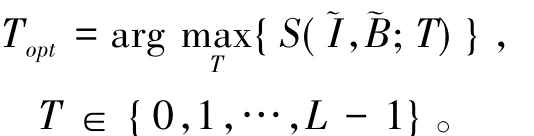
其中,式(3)中权重参数λ1、λ2的具体取值根据刑侦血迹图像分割效果普遍较好时的经验值进行选取。
3 实验结果及分析
为验证本文算法的有效性,实验选取不同环境下,具有代表性的3幅刑侦血迹图像进行单阈值分割。测试图像分别为表面较粗糙砂粒地上溅落状血迹、土地上渗透状暗红血迹、水泥地上流柱混合滴落状鲜亮血迹,分别如图1中(a)~(c)所示。

图1 刑侦图像
同时,将本文算法与 Ostu 法[19]、最大熵法[20]、指数型模糊散度(Exponential Fuzzy Divergence,EFD)算法[21]、指数型直觉模糊散度(Exponential Intuitionistic Fuzzy Divergence,EIFD) 算法[7]进行对比。其中,EFD、EIFD算法中隶属度函数分别选取Gamma 型[21]、指数型限制等价函数[7];EIFD 算法中 λ 取 0.8。
算法的参数设置如下,滤波半径r=10,空间域标准差 σd=5.2,值域标准差 σr=0.12。针对血迹图像,通过大量实验测试,确定相似度中权重参数λ1=0.1、λ2=0.82。
将3幅刑侦血迹图像转化为灰度图像,如图2~4中(a)所示。4种对比算法及本文算法针对血迹灰度图像的分割结果如图2~4中(b)~(f)所示。

图2 图像#252分割结果

图3 图像#259分割结果

图4 图像#282分割结果
对刑侦图像#252,由图2中(b)~(e)可知,Ostu法、EFD及EIFD算法均不能将血迹提取出来,最大熵法的分割效果明显有所改进,但血迹周围仍有大量噪声。对刑侦图像#259和#282,由图3~4中(b)~(e)可知,Ostu法、最大熵法及EFD算法均无法克服背景噪声的干扰,EIFD算法可减弱这种情况,但在血迹上却存在将目标错分为背景的现象。
实验表明,4种对比算法中,Ostu法主要考虑像素灰度级的均匀性,适用于目标和背景面积接近的图像,但忽略了空间信息,对噪声十分敏感;最大熵法更多考虑灰度级概率信息,可以较好分割图像中的小目标;EIFD算法更加全面描述灰度信息的不确定性,较EFD算法能有效提取目标,但其模糊隶属度中含有影响分割效果的参数。本文算法构造了不含参数的图像直觉模糊模型,并结合双边滤波,在提取血迹的同时,有效抑制噪声且保留目标边缘,分割效果较好。
为进一步对各算法的分割效果进行客观评价,以区域均匀性(Region Uniformity,RU)、区域对比度(Region Contrast,RC)作为评价指标[22]对各算法的分割性能进行定量分析。其中,区域均匀性、区域对比度分别反映区域内元素的一致性和区域间差异,取值范围均为[0,1],该值越接近1,表明分割效果越好。计算公式分别为
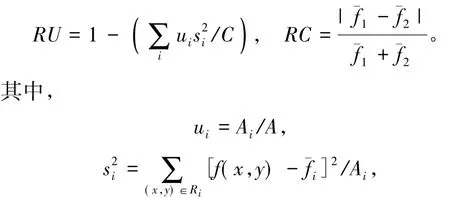

Ri表示分割后的第i个区域(i=1,2),Ai表示区域Ri中的像素总个数,A表示图像中像素总个数,f(x,y)表示像素点(x,y)处的灰度值,fmax、fmin分别表示图像灰度的最大、最小值。
针对图1所示3幅血迹图像的分割结果,各算法RU、RC值如表1所示。由表1可知,5种算法中,本文算法的量化指标最好,这与视觉评价结果基本一致,表明本文算法的有效性。
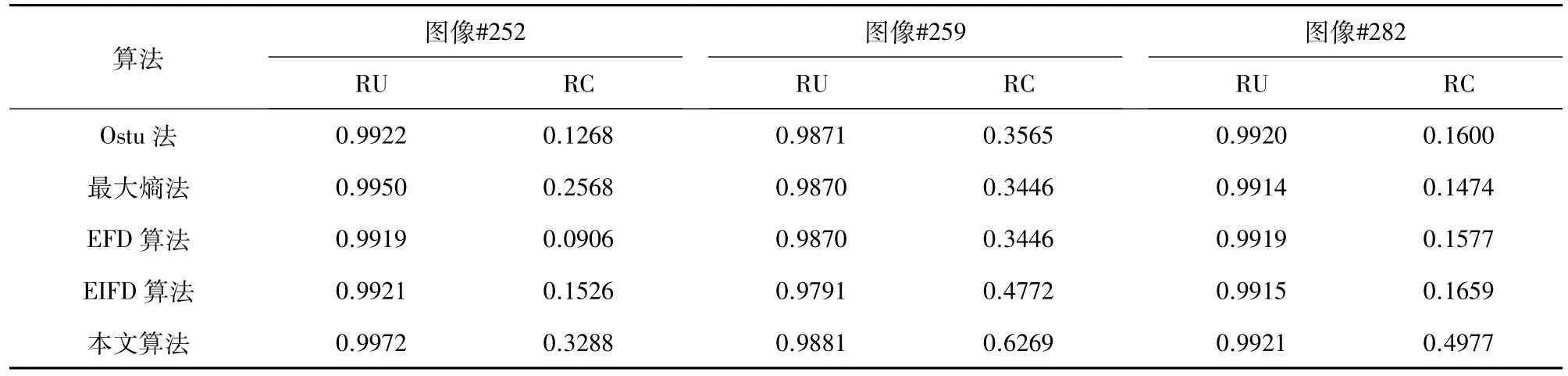
表1 5种算法RU、RC值对比
4 结语
依据直觉模糊集理论,针对刑侦图像中血迹图像,给出了一种基于直觉模糊相似度的刑侦血迹图像阈值分割算法,进行血迹提取。该算法首先采用双边滤波对血迹图像去噪,再通过“投票模型”获得图像的直觉模糊集模型,避免了传统算法模糊隶属度含参数的情况,最后采用含权重参数的直觉模糊集相似度建立目标函数,并以相似度最大为原则寻找最佳阈值。实验结果表明,该算法能在一定程度上降低噪声的影响,有效提取血迹目标的同时保留边缘等细节信息。另一方面,由于缺乏先验信息,本文算法直觉模糊相似度中的权重参数根据刑侦图像的类型取经验值,这在一定程度上限制了算法的适应性。因此,根据刑侦图像自身特性实现相似度中权重参数的自适应选取,使得该种方法适用于其他类别的刑侦图像是有待于进一步研究的工作。

