基于奇异值分解和双三次插值的图像缩放算法改进

岳 鑫，肖 晨

(1.西安工业大学光电工程学院，陕西西安710021;2.电子信息现场勘验应用技术公安部重点实验室，陕西西安710121;3.西安工业大学学报编辑部，陕西西安710021)

由于视频及图像中包含丰富的信息，公安机关经常将其作为案件的证据或者线索。现勘图像是刑侦人员为发现和收集证据而对案件有关的场所、物品等进行勘查和检验时拍摄的照片［1-2］。在现勘图像采集时，图像分辨率高、占用空间大，这些原始图片中存在过多的冗余信息，并不利于传输与处理，一般都需要采用性能良好的缩放算法进行预处理。

目前，传统的图像缩放算法主要是基于插值的算法，使用最近邻插值、双线性插值［3］或者三次样条插值［4］等技术来改变图像大小。Parker、Kenyon等人分析了各类经典空间域插值方法的性能，发现这类方法运算速度快，同时缩放后的图像视觉效果较好［5-6］。但这些算法常常无法对纹理信息或者图中相邻像素间的较大变化进行很好的处理，容易造成边缘的模糊或形成锯齿状，且传统算法多专注于对图像像素的改变，而对图像压缩改进不大。

提出一种改进的算法，对图像进行奇异值分解［7-10］，使用分解产生的矩阵进行重采样［11-12］，从而达到提高缩放图像质量且压缩图像大小的目的。

1 奇异值分解与重采样算法

1.1 奇异值分解算法

λ1≥ λ2≥ …≥ λr≥ λr+1=… =λn=0，

则存在矩阵 Um×m和 Vn×n，使得

其中

于是，σi(i=1，2，…，r)为A的奇异值。定义奇异值向量Sγ为对角矩阵S对角线元素的排列，即

那么

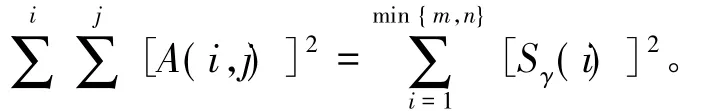
由上述定义知，矩阵经过奇异值分解后得到的非零奇异值的个数与矩阵的秩相等。因为经历了重采样后的图像块的秩小于等于原图像块，也就是说，图像块像素间的相关性增大。所以，对图像进行奇异值分解，图像块的能量将集中于对角线的左上角，序数低的奇异值将增大，而序数高的奇异值会变小。即重采样图像块的奇异值向量中，零奇异值和小奇异值的个数会增加。

1.2 重采样算法

重采样就是在矩阵元素之间引入某种相关性，一般通过对矩阵进行采样和插值实现。重采样算法的变换有线性和非线性之分，但其变换总会以线性相关性表现。重采样包括缩放变换［13］和旋转变换，通常分为下采样、插值和上采样3个步骤。不同的重采样方法，所采用的插值［14］方法也不同。

使用双三次插值［15］算法来实现重采样。双三次插值，是一种比双线性插值更加复杂的插值方式，其创造出的图像边缘也更加平滑。在二维空间中最常用的插值方法就是双三次插值。这种方法中，可以通过矩形网格中最近的十六个采样点的加权平均得到函数f在点(x，y)的值，双三次插值即使用两个多项式插值三次函数，每个方向使用一个。通过双三次插值得到的插值函数是连续的，其一阶偏导数连续，交叉导数也处处连续。

双三次插值计算公式为

插值数据的特性决定计算系数aij，如果插值函数的导数已知，使用四个顶点的高度以及每个顶点的三个导数。x与y方向的表面斜率用一阶导数h'x与h'y表示，同时在x与y方向的斜率由二阶相互导数h″xy表示。可以通过分别连续对x与y向量取微分得到这些值。将局部坐标(0，0)，(1，0)，(0，1) 和(1，1)带入这些方程，再解这16个方程，可得到网格单元的每个顶点。图1给出了双三次插值的原理，它展示了插值像素F用4×4邻域像素计算的过程。

图1 双三次插值原理

为了减少计算的复杂度，双三次插值过程通常分解为横向和纵向两个方向的插值。首先利用原像素和虚拟像素进行纵向插值，并且得到(Fh1，Fh2，Fh3，Fh4)4个像素;然后再由这4个像素通过横向插值得到像素F。

1.3 算法改进

经典缩放算法在图像缩放时只关注图像本身，未注意到在图像中存在较多无用的信息，这些无用的信息随着图像的缩放而缩放。为了解决在图像缩放同时兼顾图像本身所带信息的有效性和图像文件的大小问题，提出一种基于奇异值分解和双三次插值的图像缩放算法。

算法思想基本如下:每一个彩色图像可以看做为由RGB三通道组成的三个实数矩阵，若为灰度图像则可以看做由0到255组成的单个矩阵。由式(1)可知无论是彩色图像还是灰度图像均可分解为三个矩阵相乘的形式。三个矩阵中的中间矩阵式(2)为奇异值矩阵，且该矩阵的能量集中在左上角。在图像进行压缩时，可以利用该矩阵中能量集中在左上角的性质依次减少最少的能量，达到在压缩过程中图像损失最小的目的。图2为32×32的猴子图像及以奇异值10%为跨度取值的奇异值分解结果图像。

图2 奇异值分解

由式(1)可知，针对奇异值分解中的三个矩阵左右矩阵U和VH的重采样可以达到对图像尺寸大小的变化。其中重采样方法采用双三次插值法。以M×N的图像为例，分别对三个图像通道做如下变换。奇异值分解结果为USVH，其中S为奇异值矩阵，S对应的酉矩阵为U和V，即U为M×M矩阵，V为N×N矩阵，若想将原始M×N的矩阵缩放到M1×N1的矩阵，需要通过式(3)分别对矩阵U和矩阵V进行重采样，得到矩阵UM1×M和矩阵VHN×N1，分别记为U'和V'，最后利用公式U'SV'进行反变换。

通过上述方式，对原始图像进行缩放处理之后，得到的结果图像不仅可以达到图像缩放的目的，而且极大的减少了图像内无关的信息，使可以得到最优的结果。

2 实验与分析

针对刑侦图像数据库进行了实验测试分析。以图3所示原始图像(600×358像素)为例，使用最近邻插值法、线性插值法、区域插值法、双三次插值法、Lanczos插值法和所给改进算法进行5倍放大的结果图像如图4所示，其相应的局部图像如图5所示。从中可见，所给改进算法在视觉效果上要优于其他算法，特别是在保存图像纹理细节信息上，所给改进算法表现良好。

图3 刑侦图像

图4 放大结果

图5 (a)和图5(c)中的局部图像出现了明显的 马赛克现象，如书包带。而在文中使用算法进行放大的图像图5(f)中没有出现明显的马赛克现象。对比图5(b)和图5(g)可以发现改进算法在清晰度较线性插值法更好一些。因此改进算法的放大结果不仅保留了图像的细节信息，同时从直观来讲较最近邻插值、线性插值和区域插值有一定的优化。通过对图4(d)、图4(e)和图4(f)双三次插值法、Lanczos插值法和改进算法的对比可以看出这三种算法在视觉上无太大差异，而在客观指标中改进算法在各个指标中都略优于双三次插值法、Lanczos插值法。

图3 图像局部

评价图像缩放质量好坏的另一种方法是使用客观评价指标进行评价。使用应用较为广泛的四种评价方法对包括改进算法在内的6种算法缩放结果图像进行评价。评价方法分别为反应图像平均亮度的均值、反应图像灰度级分散程度的图像标准差、反应图像清晰程度的图像平均梯度和反应图像平均信息量的图像熵。

图像像素的均值，反映了图像的平均亮度，平均亮度越小，图像质量越差，设待评价图像为F，大小为M×N，其均值计算公式为

图像像素灰度值相对于均值的离散程度用标准差(Standard Deviation)表示。如果标准差越小，表明图像中灰度级分别越集中，图像质量也就越差。设待评价图像为F，大小为M ×N，均值为u，其标准差计算公式为

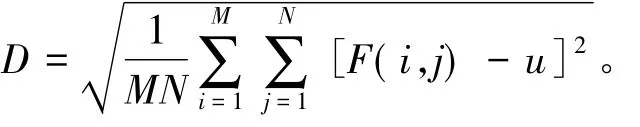
图像中细节反差和纹理变换用平均梯度来反映，图像的清晰程度其在一定程度上也能反映。设待评价图像为F，大小为M×N，其平均梯度计算公式为

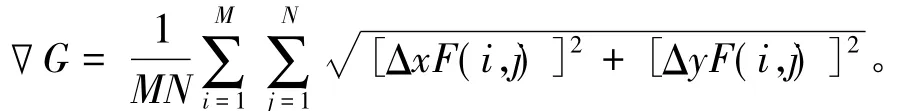
式中，ΔxF(i，j) 和 ΔyF(i，j) 分别表示像素点(i，j)在x或者y方向上的一阶差。

图像的平均信息量用熵来表示，他从信息论的角度衡量图像中信息的多少，图像中的信息熵越小，说明图像包含的信息越少。其计算公式为

其中，灰度值l在图像中出现的概率为P(l)，图像的灰度级为L，对256灰度等级的图像，L=255。

各种算法在5倍、2倍、0.5倍和0.2倍缩放比例下，结果图像均值指标对比情况如表1所示。在6种算法中放大5倍和放大2倍时改进算法均值指标均高于其他算法，在缩放0.5倍时改进算法排第四，但与第二只有0.09%的差距，与第一有0.21%的差距，可以认为是基本一致的。在缩放0.2倍时，改进算法均值指标排第二，较第一有1%的差距。总体上在均值方面改进算法表现良好。

表1 均值指标对比

各种算法在不同放大比例下，结果图像标准差指标对比见表2。从表中可知，改进算法在标准差指标上较为稳定，只有0.4%的浮动。在图像放大时，除线性插值法外的其他算法基本一致且要优于线性插值法。在图像缩小时，改进算法要优于或等同于除最近邻插值法外其他算法，且与最近邻插值法只有 1.26%的差距。在缩放 5 倍、2 倍、0.5 倍、0.2倍下，分别在第一、第三、第五和第四名，即使在最差的缩放0.5倍时也与第一只有0.47%的差距，且在最好时可以超过区域插值法约4.5%。可以认为在标准差指标上这6种算法效果基本一致，即6种算法的灰度分布较为统一。

平均梯度是反应细节反差和纹理变换的一种指标，在一定程度上反应出图像的清晰度。各种算法在不同缩放倍数下平均梯度指标对比见表3。在放大5倍时最邻近插值法和区域插值法在指标上均好过改进算法，但是这两种算法从主观评价上产生了较多的马赛克现象，放大倍数越大，其马赛克现象越严重。在本算法中，避免了该问题的产生。在缩放0.2倍时改进算法较区域插值法提高了32.6%。

表4为各种缩放算法在不同缩放倍数下熵对比，熵代表了图像的信息量，在图像放大的过程中图像的信息量基本不会损失，由该表可以看出在各种缩放倍数下包括改进算法的这6种算法计算的结果图像对原图像信息保留结果较为一致，且相差不到1%。在图像缩小时图像的信息会有一定的损失，在缩放0.5倍和0.2倍时，改进算法保留了较多的图像信息。

表5为各算法在各个缩放倍数下结果图像的文件大小概况。由图可知，改进算法无论在对图像进行放大操作还是缩小操作时，均可减少文件大小，且远小于其他五种算法的结果图像文件大小。在5倍缩放倍数下改进算法较其他算法减少了73%～58.5%的文件体积，在2倍缩放时减少了60%～50.7%的文件体积，在缩放0.5倍和0.2倍时分别减少了 55.8%～40.1%和 49.1%～42%的文件体积。改进算法在文件体积上有较大的优化。

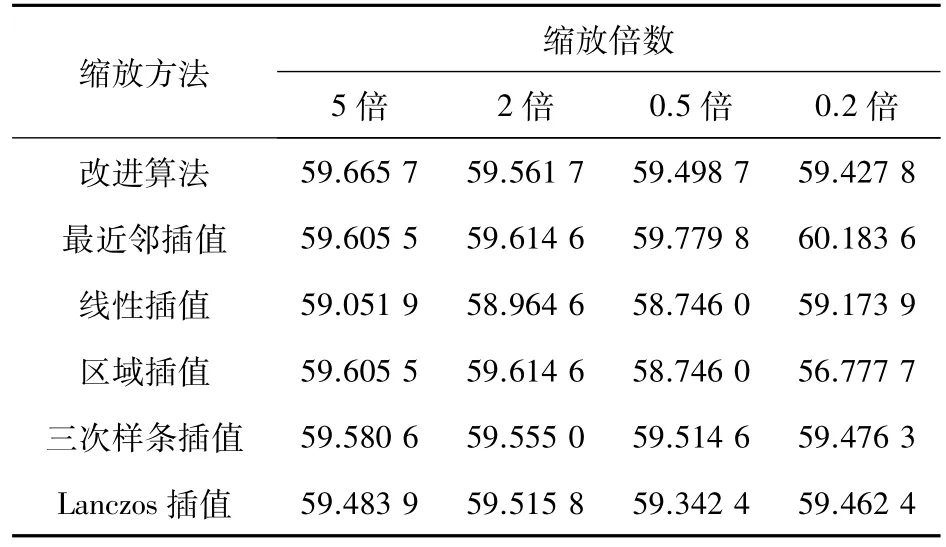
表2 标准差对比

表3 平均梯度对比

表4 熵对比

表5 文件大小对比/kb

3 结语

提出基于奇异值分解和双三次插值缩放算法的改进。利用奇异值分解方法将图像矩阵分解为三个小矩阵相乘的形式，采用双三次插值算法将乘式中左右矩阵进行重新采样，经过重构得到缩放结果图像。实验表明，改进算法可以完成对图像的缩放，能在有效缩放的同时减小图像文件大小。经过实验，并与传统缩放算法进行比较和对缩放结果图像的客观指标的计算，发现通过该算法结果图像的客观图像评价指标略优于其他算法指标，结果图像文件大小远小于其他算法结果图像。