两种群Lotka-Volterra互惠生态系统的β绝灭和β持续生存

阎 慧 臻, 刘 燕, 苗 苗

( 大连工业大学 信息科学与工程学院, 辽宁 大连 116034 )

0 引 言

种群生态学是生态学的一个重要分支，也是生态学中数学应用最多的一个分支。二维Lotka-Volterra模型是描述两种群相互作用的最为经典的数学模型，按其生态意义可分为三类：捕食与被捕食模型(例如食草动物与草、天敌与害虫)、竞争模型(例如虎群与豹群、庄稼和野草)及互惠模型(例如蜜蜂与花朵)。许多学者对Lotka-Volterra模型做了大量的研究[1-4]，这些研究大都是针对模型非平凡解的定性分析。由解的唯一性定理可知，任一初值为正的解在有限时间内都不可能变为零，换句话说，无论种群数量为多少，生物体内的毒素有多少，在有限时间内种群都不可能绝灭，这显然与实际不符。在现实中，如果种群数量过少或环境中毒素浓度过高，种群都将无法生存而迅速绝灭。为了使模型能更真实地反映实际，马知恩等[5]研究了种群在有限时间内的绝灭和持续生存问题，提出了β绝灭与β持续生存的概念。文献[6]研究了污染环境中一维Lotka-Volterra模型的β绝灭与β持续生存问题，给出了种群β绝灭与β持续生存的充分条件。文献[7]研究了一类个体模型在有限时间内的绝灭与持续生存问题，给出了个体β绝灭与β持续生存的充分条件。文献[8]和文献[9]分别研究了二维Lotka-Volterra 捕食与被捕食系统和竞争系统的β绝灭与β持续生存问题。本文在以上研究的基础上讨论了两种群Lotka-Volterra互惠生态系统在有限时间内的绝灭与持续生存问题，给出了两种群β绝灭与β持续生存的一些充分条件。

1 数学模型及定义

考虑二维Lotka-Volterra系统：

式中：a11>0，a22>0，即两种群x1(t)，x2(t)都满足密度制约。两种群在一个相同的自然环境中生存，按其生态意义，它们之间的相互作用可分以下3种情况：

(1)捕食与被捕食

当系统(N)中的参数a12>0，a21<0，此时x1(t) 为被捕食者(即食饵)，x2(t)为捕食者。并假设r11>0，r21<0，此时捕食者x2(t)仅以食饵x1(t)为食。

(2)相互竞争

当系统(N)中的参数r11>0，r21>0，a12>0，a21>0，此时两种群中每一个种群的存在都会抑制另一个种群的增长。

(3)互惠共存

当系统(N)中的参数a12<0，a21<0，此时两种群中每一个种群的存在都会促进另一个种群的增长。并假设r11>0，r21>0，即两种群除相互为食外，同时还有其他的食物来源。

对应于以上3种情况，系统(N)被分为3类：捕食与被捕食模型、竞争模型、互惠模型。

为便于书写，给出下面记号：

令

Δ=detA=a11a22-a12a21

Δ1=a22r11-a12r21

Δ2=a11r21-a21r11

并假设Δ>0，Δ1>0，Δ2>0，此时系统(N)中的两种群x1(t)，x2(t)是永久持续生存的[10]。

2 主要结果

定理1考虑互惠模型(N)

证(1) 用反证法，假设t∈[0，+∞) 时，x1(t)>β。

由式(1)及式(2)式可得

令

由上极限的性质知，对于任意给定的ε1>0，ε2>0，必存在T>0，当t≥T时，

r11-a12〈x2〉≤λ1+ε1r21-a21〈x1〉≤λ2+ε2

将其代入式(3)及式(4)得

即

由引理知：

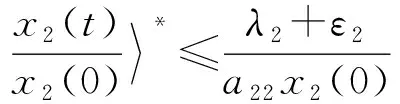
由ε1、ε2的任意性知：

所以

即

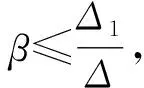
所以种群x1(t)必在有限时间内β绝灭。

(2)的证明类似于(1)(略)。

定理2考虑互惠模型(N)

(1)对于种群x1(t)，

(2)对于种群x2(t)，

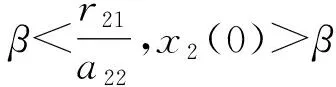
证明(1)(Ⅰ) 因为x1(0)>β，所以由x1(t)的连续性知存在δ>0，当t∈0，δ时，x1(t)>β。

下面说明x1(t)>β可无限延拓下去。否则，设x1(t)>β仅能延拓到某个半开半闭区间[0，η)上，则x1(η)=β。

在[0，η]上

因为x1(0)>β，所以由微分方程的比较定理可知，x1(t)>β，t∈[0，η]。

所以x1(η)>β，矛盾！

故x1(t)>β可无限延拓下去，即：x1(t)>β，t∈[0，+∞)。

所以x1(t)永远β持续生存。

证因为x1(T)>β，所以存在δ1>0，使得t∈[T，T+δ1]时，x1(t)>β。

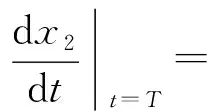
(ii)证明(i)中不等式可无限延拓下去。否则，设(i)中不等式只能延拓到某个半开半闭区间[0，η)上。由(i)的证明可知：

在[0，η]上

a11x1(β-x1)

因为x1(0)>β，所以由比较定理可得：x1(t)>β，t∈0，η，所以x1(η)>β，矛盾！

由(i)(ii)的证明可知：种群x1(t)永远β持续生存。

(2)的证明类似于(1)(略)。

3 结 论

对于种群x2(t)的分析完全类似于种群x1(t)(略)。

4 数值模拟

Matlab绘图程序如下：

a11=2;

a22=4;

a12=-3;

a21=-1;

r11=1;

r21=1;

beta=2;

ds=@(t，s)[s(1)*(r11-a11*s(1)-a12*s(2));s(2)*(r21-a21*s(1)-a22*s(2))];

s0=[4;1];

tf=100;

[t，s]=ode45(ds，[0 tf]，s0);

b=beta*ones(size(t));

%绘图

axis([0 tf 0 6.5]);

hold on

plot(t，s);

plot(t，b，′r′);

执行程序后得x1(t)、x2(t)的图形如图1所示。

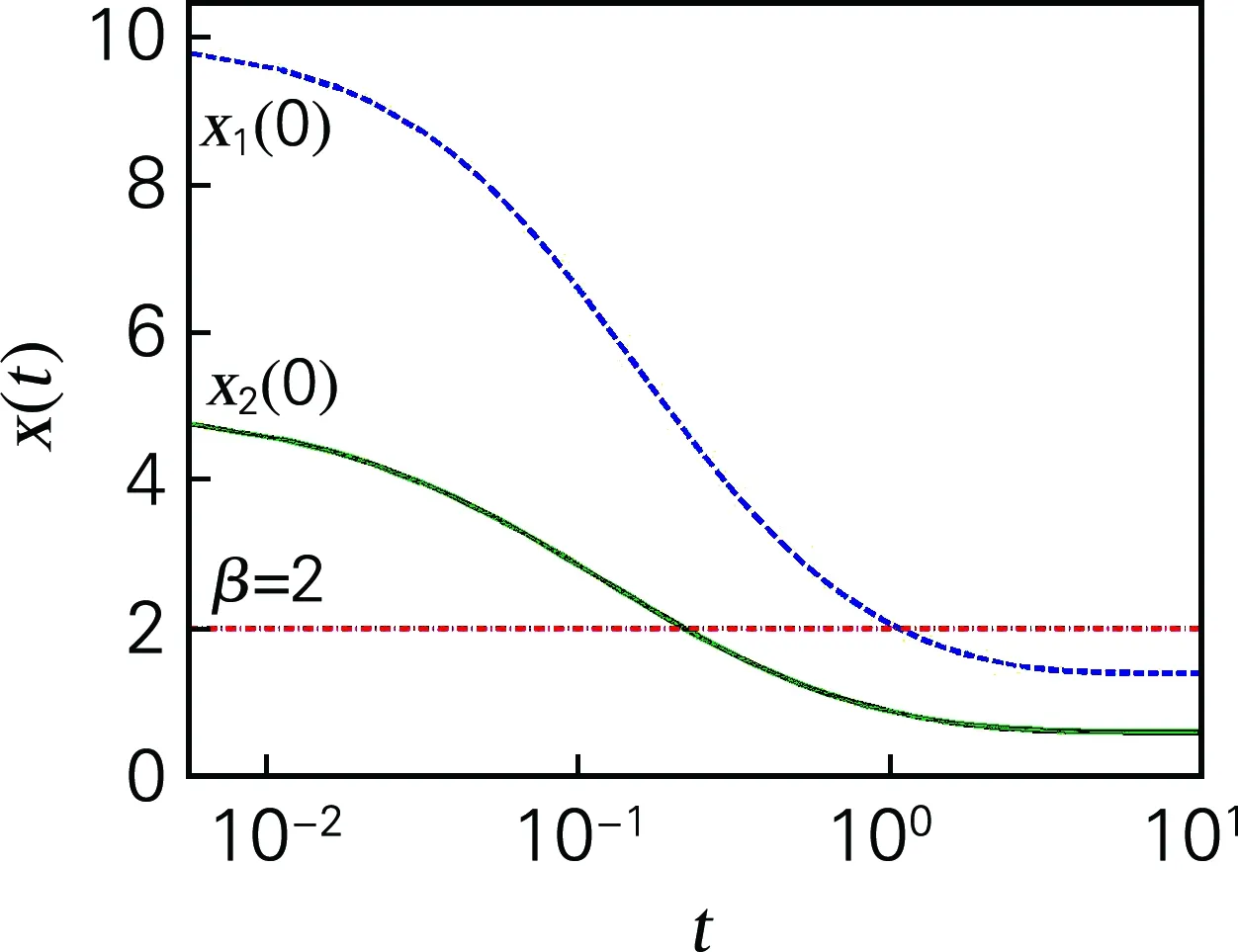
图1 种群β绝灭示意图

由图1可以看出，x1(t)、x2(t)在有限时间内均β绝灭，与定理1的结论一致。

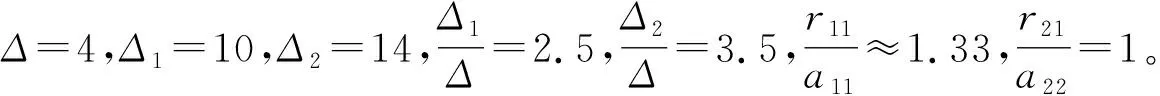
(1)取β=1，x1(0)=4，x2(0)=1，执行Matlab程序得x1(t)的图形如图2所示。

图2 种群x1(t) β持续生存示意

由图2可以看出，x1(t)永远β持续生存，与定理2中(1)(Ⅰ)的结论一致。

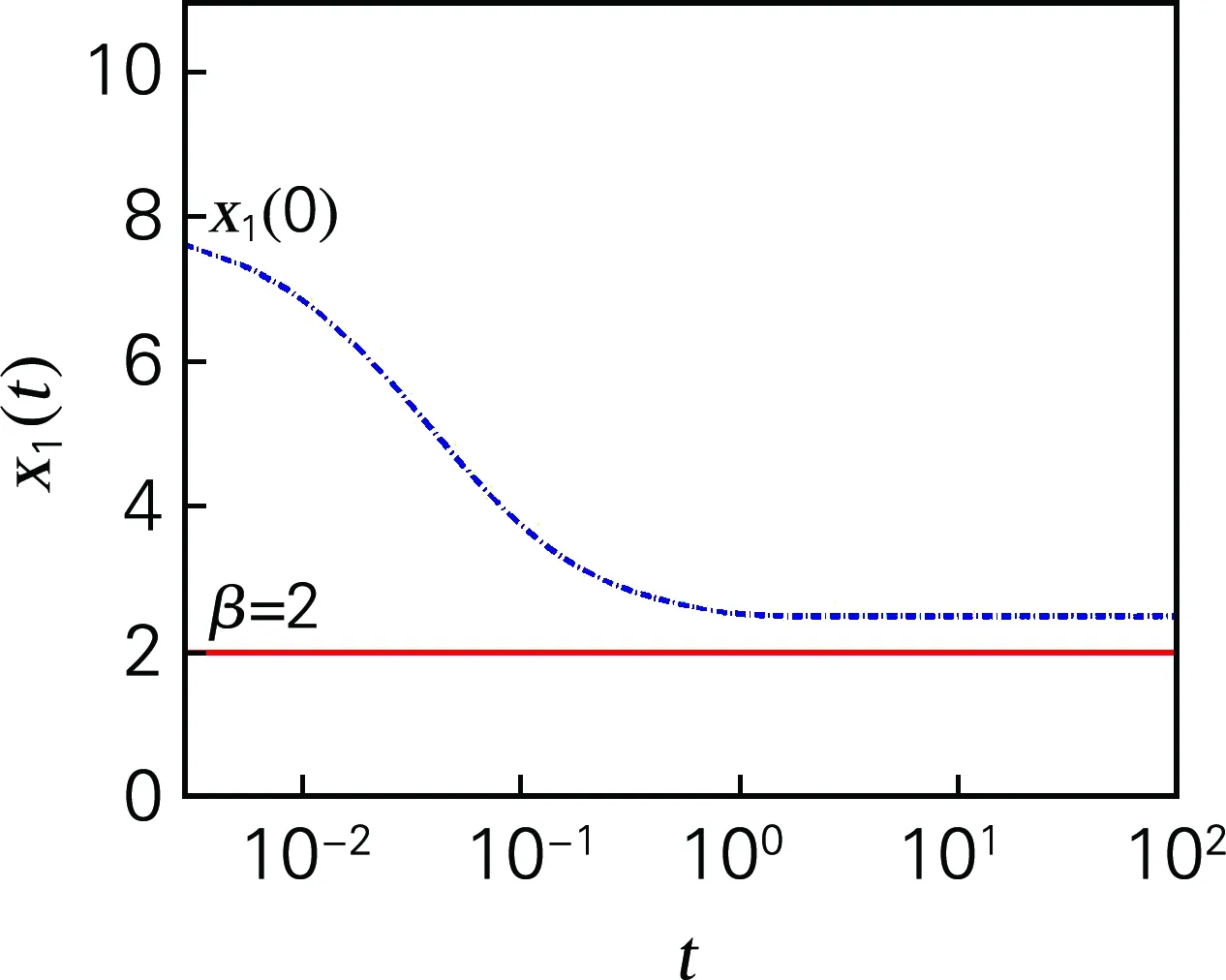
图3 种群x1(t)的β持续生存示意图

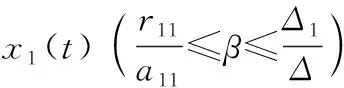
由图3可以看出，x1(t)永远β持续生存，与定理2中(1)(Ⅱ)的结论一致。

(3)取β=0.9，x1(0)=1，x2(0)=6，执行Matlab程序得x2(t)的图形如图4所示。

图4 种群x2(t)的β持续生存示意

由图4可以看出，x2(t)永远β持续生存，与定理2中(2)(Ⅰ)的结论一致。

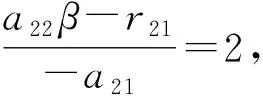
由图5可以看出，x2(t)永远β持续生存，与定理2中(2)(Ⅱ)的结论一致。

图5 种群x2(t)的β持续生存示意图