基于BP神经网络的铁路轨道几何不平顺预测方法

彭丽宇， 张进川， 苟娟琼， 李学伟

(北京交通大学 经济管理学院， 北京 100044)

合理养护维修计划的制定一直是铁路工程领域(铁路工务管理)的一个重要问题，而该计划的确定及实施要求对当前的轨道质量状况进行适当(科学)的评估与准确的预测，而轨道几何状态是轨道、载荷、路基和自然因素等共同作用的结果[1]，不易于评估。作为反映轨道质量的主要数据源，轨道几何状态数据主要通过人工静态检测与轨道检测车(以下简称轨检车)动态检测获得。多年的线路运营积累了大量的轨道几何状态数据，但限于数据分析水平与挖掘深度的不足，数据并未得到充分利用。

基于轨检车的检测资料，对轨道状态变化进行发展规律分析和预测是一个重要研究方向。国内外相关机构和学者对高速铁路和部分既有线的轨道不平顺进行了大量研究。早期日本学者[2-5]基于大量实验数据，通过回归分析得到的高低不平顺线性与非线性预测公式；James[6]将分形理论用于评价轨道平顺状态，并利用双分析方法对高低不平顺进行预测，Daniel[7]使用了卡尔曼滤波方法对轨检车数据进行预测分析；国内学者也相继提出了轨道不平顺线性预测公式[8-9]、非线性预测模型[10]、综合因子法[11]、基于时间序列的非等时距灰色时变参数模型[12]以及基于非等时距加权灰色理论和神经网络法的组合预测方法等[13]。

这些研究成果对轨道质量发展预测进行了有益探索，但是重载铁路由于存在运量大、轴重大、密度大的特点，其轨道平顺状态预测研究还相对欠缺。

本文基于轨道不平顺变化的特点，结合神经网络的非线性映射能力，使用BP神经网络对线路轨道不平顺的状态进行了预测。为了进一步验证文中提出的网络模型有效性，利用某重载铁路线路的轨道不平顺检测数据进行了验证，并与多元多重回归模型所得预测结果进行了对比。计算结果显示，双隐层神经网络具有较高的预测精度，能够用于重载铁路轨道质量预测。

1 理论模型

1.1 多元多重回归模型

多元回归模型是用来对多变量进行回归分析的数学模型，通常含有多个自变量与一个因变量。当该模型用于分析多个因变量与多个自变量的依赖关系时，则称为多元多重回归模型，其模型结构为

( 1 )

式中：x1,x2,…,xm为自变量；y1,y2,…,yp为因变量；β为模型参数；ε～N(0,σ2)为随机误差。该模型的矩阵表示形式为

( 2 )

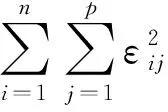
利用拉直法及矩阵四块求逆公式求解此二次规划问题，可以得到模型参数的估计值，具体步骤这里不再赘述。

1.2 BP神经网络模型

BP(Back Propagation)神经网络是一种按误差反向传递算法训练的多层前馈型神经网络，一般由3层组成，即输入层、隐层(由一层或多层组成)和输出层，见图1。

BP神经网络在输入层与输出层之间增加若干层(一层或多层)神经元，这些神经元称为隐单元。在其结构中，神经元在层与层之间是全连接，而在层内部则是无连接的。各隐层节点采用Sigmoid激励函数，输出层激励函数根据应用的不同需要而有所不同[14]。

误差反向传递算法(BP算法)主要有两个学习阶段：信号正向传播阶段，隐层通过处理经过输入层的信息来计算每个单元的实际输出值；误差反向传播阶段，如果不能获得期望的输出值，则通过以逐层递归的形式计算实际输出与期望输出之差值(即误差)，从而以此差值来调节权值。BP算法的基本步骤如下：

Step1设置初始权值为较小的随机非零值。

Step2给定输入/输出样本集合{up,yp}p，重复下列过程至满足收敛条件(Eall≤ε)：

(1) 对于每个样本，计算正向过程

( 3 )

式中：I、J分别为输入层与隐层节点数；wkj、wji分别为输入层到隐层、隐层到输出层的权值；f1、f2分别为隐层与输出层的激励函数；ojp为隐层第j个节点的输出；dip为输出层第i个节点的输出。

(3) 计算各层节点误差

( 4 )

(4) 修正权值

( 5 )

式中：η为权重更新步长。

Step3步长选择。

在BP算法中，步长η的选择很重要，η大则收敛快，但是过大则可能引起不稳定(η最大不能超过2/λmax，λmax为输入向量的自相关矩阵的最大特征值)；η小可避免振荡，但收敛速度变慢，为解决此问题可采用广义delta规则。

2 基于神经网络的轨道不平顺状态预测模型

轨检车检测数据是评价线路轨道质量状态的主要依据。本文选取某重载铁路K420+000～K426+000共6 km的轨道不平顺检测数据，对每个200 m区段分别计算左右高低、左右轨向、轨距、水平、三角坑的单项标准差，用于BP神经网络模型训练与预测。数据的检测时间为2016年1月到2017年6月，期间每月中旬检测一次，共18组数据。图2为K422+000～K422+200区段的七项标准差随时间变化曲线。

由于2016年6月至7月之间的线路维修，高低不平顺标准差明显减小；维修前后，各项不平顺标准差均呈逐渐增大趋势。其他区段的数据也有相同特征。以下详细介绍BP神经网络模型的构建过程与应用分析。

2.1 BP神经网络模型的构建

BP神经网络构建过程主要是对合理的模型参数进行选取[15]，具体包括：

(1) 网络层数的确定。合理的网络结构模型的精度至关重要，本文分别设计了包含单隐层和双隐层的BP神经网络，用来对线路不平顺状态进行预测。

(2) 输入输出层神经节点数目的确定。输入输出层神经节点的数目依赖于网络目的和数据类型。由于该网络主要用于轨道质量预测，数据为7项轨道不平顺的标准差，属于多维时间序列预测问题。模型输入为历史数据，输出为当前数据；历史数据量过小，难以提供足够信息量；历史数据量过大，将减少输入输出样本数目，降低模型预测能力。经过综合考虑，本文确定将3期历史数据作为输入，则输入层节点数为21；将当前数据作为输出，则输出层节点数为7。

(3) 隐层节点数目的确定。隐层节点数目与输入输出数据有关，可以通过经验法确定。对于单隐层和双隐层的BP神经网络，本文允许节点数目在合理范围内变化，分别计算不同隐层节点数目的BP神经网络对6 km数据的平均预测精度(均方误差MSE)，选取精度最高的节点数目，计算结果见图3。由该图可知，单隐层神经网络的隐层节点数应取10，双隐层神经网络的第一、第二层节点数应分别取12和9。

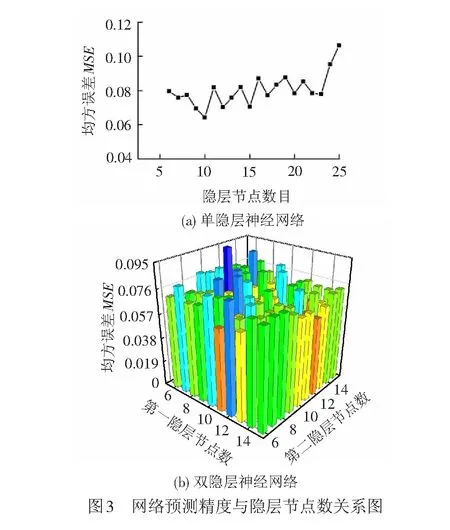
(4) 激励(传递)函数的确定。在BP神经网络中，隐层和输出层节点的输入输出之间具有函数关系，这个函数称为激励函数。Sigmoid函数连续、可导、有界，是关于原点对称的增函数，也是常用的激励函数。在使用Sigmoid函数之前需要将网络的输入和输出值归一化处理于区间[-1,1]内。

(5) 训练方法的确定。基于Levenberg-Marquardt(LM)规则的训练方法不但收敛速度快，而且运算次数和花费时间是所有的改进算法中最少的，虽然存在内存占用大的问题，但是本文输入输出节点数目较少，所以基于LM规则的训练函数仍然是最好的选择。

(6) 性能函数的确定。性能函数用于评估网络的预测精度。一般选择计算误差来充当性能函数的功能。常见的有均方误差(MSE)和平均相对误差(MPE)等，其计算公式为

( 6 )

( 7 )

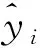
2.2 神经网络的预测精度分析

本节分别采用单隐层和双隐层的BP神经网络，对图2中的数据进行建模分析。为了去除线路维修的影响，本文忽略2016年7月的检测数据，将3期历史数据作为输入，1期当前数据作为输出；同时将2017年2月前的数据用于模型训练，之后的数据用于模型测试。模型的训练与预测结果见图4。

受2016年7月线路维修的影响，该次数据不能用于构造输入输出数据，导致2016年7月～10月无预测数据。通过模型预测的结果可以看到，预测值与实际的数据吻合度较高，误差在允许的范围之内，因此可应用该模型对未来的数据进行预测。

2.3 不同模型计算结果精度对比

为了进一步检验模型的精度，本文对多元多重回归模型、单隐层神经网络、双隐层神经网络的预测误差进行了对比，见表1。表中结果为K420+000～K426+000范围内30个区段的统计平均值。

表1 不同方法预测结果误差对比表

从预测误差结果对比可以看出：

(1) 从整体上看，模型精度高低顺序依次是：双隐层BP网络模型、单隐层BP网络模型、多元多重回归模型；从平均相对误差上看，由大到小分别是：多元多重回归模型、单隐层BP网络模型、双隐层BP网络模型。

(2) 同单隐层BP网络模型相比，双隐层BP网络模型整体精度要更好，这从一定程度上说明随着隐层数的增加，有助于提高网络预测精度。

3 结束语

本文根据轨道不平顺的变化特点，针对轨道不平顺状态，利用BP神经网络对左右高低、左右轨向、轨距、水平、三角坑七项检测数据的区段标准差进行预测，结果显示本文提出的BP神经网络可以对轨道的不平顺状态进行准确地预测。

从预测结果来看，双隐层BP网络模型比单隐层BP网络模型和多元回归分析模型具有更高的预测精度，这从一定程度上说明随着隐层数的增加，有助于提高网络预测精度；但相对比单隐层BP网络模型，预测精度并无显著提高。

总之，通过分析获得的轨检车数据，可以从中掌握线路不平顺的动态质量，以便能够科学的指导线路养护维修工作，有效评估工务部门的工作质量，从而实现轨道的科学管理工作。