基于Mesri蠕变模型的路基工后沉降计算方法研究

肖 东， 蒋关鲁， 马小斐， 赵乾维， 高方东， 戚志慧

(1. 西南交通大学 土木工程学院， 四川 成都 610031； 2. 四川省交通运输厅公路规划勘察设计研究院， 四川 成都 610041；3. 招商局重庆交通科研设计院有限公司， 重庆 400067)

当今，高速铁路俨然成为我国走向世界的重要名片，其以快速、舒适、平稳、安全等特点正改变着人们的出行方式，而这些特点的实现离不开线下工程严格的工后沉降控制标准。相比桥梁、隧道，路基工后沉降的控制更加困难且预测难度也更大。因此，如何有效地计算路基工后沉降一直是工程界的重要课题。对路基工后沉降研究，国内外学者提出了诸多沉降预测模型[1]，如泊松模型、指数模型、双曲线模型及对数模型等。这些方法的问题在于都要求荷载在瞬时一次施加，而路堤荷载是逐级施加的[2]；同时，还存在一个不足之处，即预测模型是建立在前期沉降观测资料的基础之上进行曲线拟合得到的，这很难应用于新建路基工程。另外，还有一类是经典固结理论结合土体本构模型的算法，此类方法参数较多，物理意义不明确，且参数的确定需要进行大量的三轴试验及固结试验，不仅耗时还很难得到可靠的参数取值，因而在实际工程中难以被采用[3]。

对工后沉降的计算，如何考虑土体的应力应变时间效应(流变特性)至关重要。在众多描述土体流变特性的模型当中，Mesri蠕变模型[4]因其对土类适用性强、表达形式简单及参数少而得到广泛应用。因此，本文在Mesri蠕变模型的基本框架内引入路基荷载下受路基宽高比影响的地基附加竖向应力解析式，并结合路基多级堆载的特点，提出了一种工程上简单、实用的路基工后沉降计算方法，最后将路基工后沉降的计算结果与离心模型试验数据进行对比分析。

1 工后沉降计算方法

1.1 计算假定

一般地，路基工后沉降由地基压缩沉降和路基本体压密变形两部分组成。由于路基本体在填筑时具有较高压实度和刚度，自身的压缩变形很小。大量现场实测资料表明[5]，路基本体的最终沉降一般不超过路基填高的千分之一，虽然也表现出蠕变特性，但其蠕变速率及蠕变总量都很小[6]，相反地基土沉降则占据主导地位；另一方面，由于路基工程的地质条件往往复杂多变，不同地区土体的物理力学指标千差万别，以致其压缩变形特性显著不同，且具有很强的区域性，相较于路基本体，地基土沉降预测难度要大得多。可见，地基土压缩变形的准确计算是成功预测路基工后沉降的关键。因此，为简化计算模型，本文实际上研究的是路基堆载下地基沉降计算方法，而未考虑路基本体的压缩，这在工程初步设计阶段是可行的。没有特殊说明下文所述的路基工后沉降专指地基土工后压缩变形。

另外，假定在工后起始阶段地基土主固结沉降已基本完成，并将其作为计算蠕变变形的时间起点。然而对于深厚软黏土地基，由于渗透固结时间长，难于界定主、次固结的分界点[2]，也就无法通过蠕变变形来计算工后沉降。因而，对于软黏土这类渗透性相当低的地基土不属于本文研究范围。

1.2 Mesri蠕变模型推导

(1) Singh-Mitchell蠕变方程

在分析总结大量土体蠕变试验成果的基础上，Singh-Mitchell[7]认识到土体应力-应变曲线采用指数关系、应力-应变-时间曲线采用幂次关系能较好地反映土体的蠕变特性，并提出了关系方程

( 1 )

( 2 )

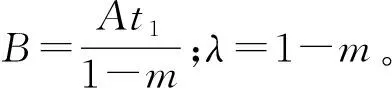
(2) 双曲线型应力-应变模型

Kondner[8]提出了双曲线型应力-应变方程，它可以很好地描述土体从零应变至破坏应变的应变硬化行为，该方程为等轴双曲线，其表达式为

( 3 )

由式( 3 )可得初始切线模量

( 4 )

再由式( 3 )求极限值ε→∞，得最终主应力差

( 5 )

容易看出，在双曲线型应力-应变模中，只有当应变为无穷大时才能达到最大主应力差(σ1-σ3)ult。而实际上，土体破坏剪应力(σ1-σ3)f往往在有限应变εf状态下即可达到。为了使双曲线经过试验所观测到的土体破坏点(εf,σ1-σ3)，特引入破坏比的概念

( 6 )

将式( 4 ) ～式( 6 )代入式( 3 )，得

( 7 )

(3) Mesri蠕变模型

将式( 2 )与式( 7 )相结合可得到Mesri蠕变方程[4,9]

( 8 )

( 9 )

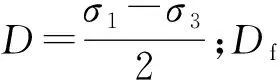
(10)

式中：c、φ和k0分别为地基土的黏聚力、内摩擦角及静止土压力系数；σz为附加竖向应力。

当t=t1时，式( 5 )等价于

经代数变换得

(11)

1.3 附加竖向应力

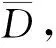
(12)

式中：α1、α2、α3为系数，可由地基土性质及路基坡率来确定；B、b分别为路基底、顶面宽度；h为填高；γ为路基填土重度；G为沿走向单位长度的路基填土荷载；h′为等效荷载高度；b′为等效荷载宽度，各参数意义在图1中均有明确标识。路基反力的分布形式，就可以通过弹性理论积分求出路基荷载引起的地基中各点的附加应力。

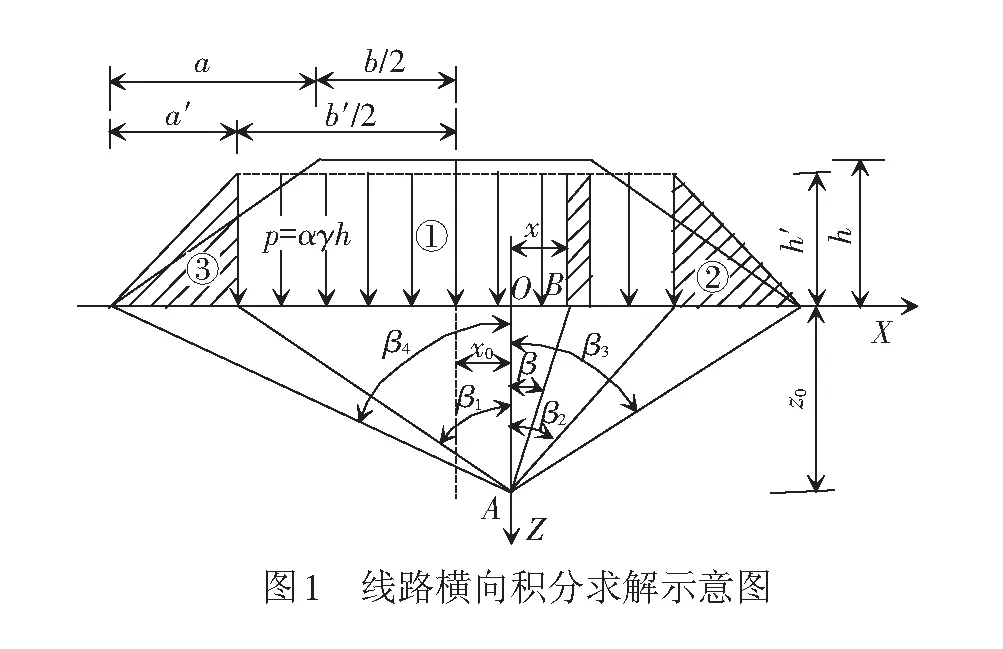
Boussinesq利用弹性理论导出弹性半无限体表面作用一集中力时内部任一点的应力表达式(图2)

(13)

式中：P为集中力；z为计算点至表面垂直距离；R为计算点与荷载作用点距离。

(14)

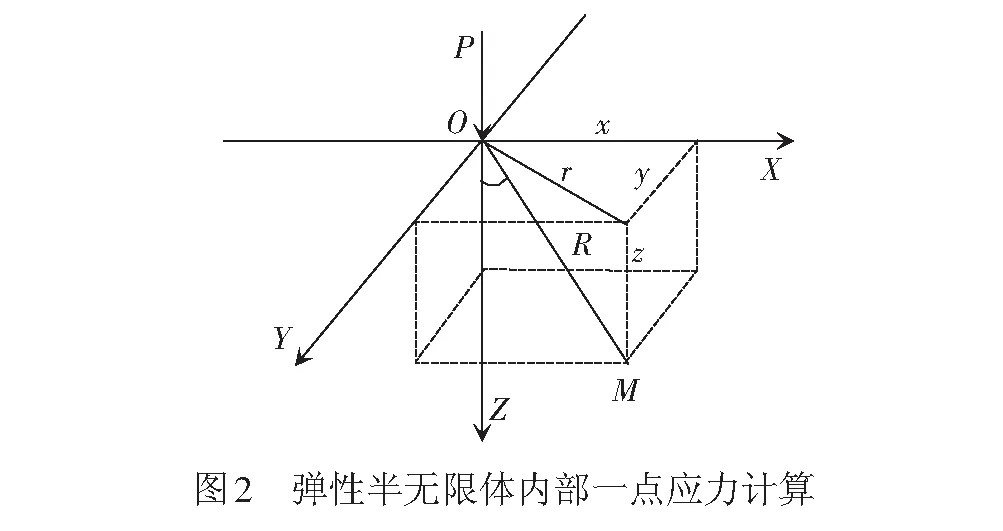
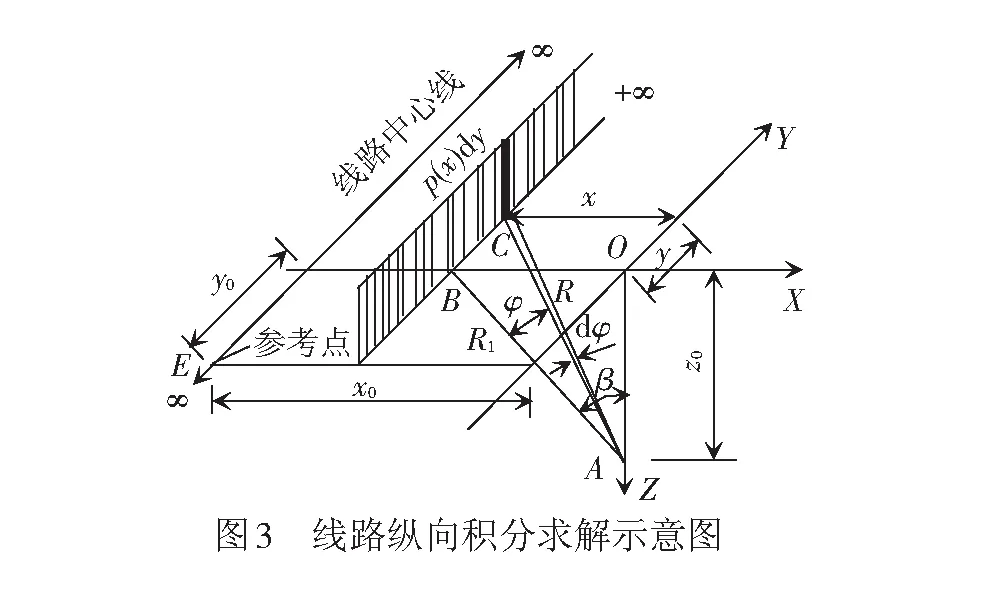
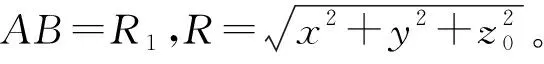
式(14)可转化为

(15)

根据三角函数关系得到y=R1tanφ，则dy=R1/cos2φdφ，且R1=Rcosφ，R1=z0/cosβ

(16)

在横断面上，荷载由三部分组成，地基中任一点的附加应力由每一部分荷载叠加而成，即

σz=σz1+σz2+σz3

(17)

式中：σz1为均布荷载在地基中产生的附加应力，对应图1中的①号区域；σz2为右边三角形荷载产生的附加应力，对应图1中的②号区域；σz3为左边三角形荷载产生的附加应力，对应图1中的③号区域。

(1)σz1表达式

根据图1中①区域，由σz=σz1+σz2+σz3，x=x1得β=β1，x=x2推得β=β2，p(x)dx=pR1/cosβdβ代入式(16)，得

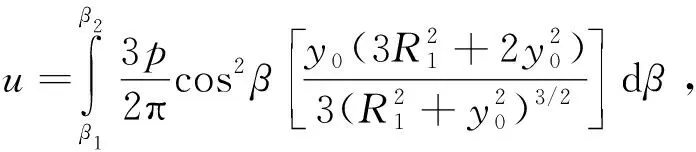
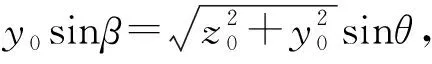
将式(12)代入可得

(18)

(2)σz2表达式

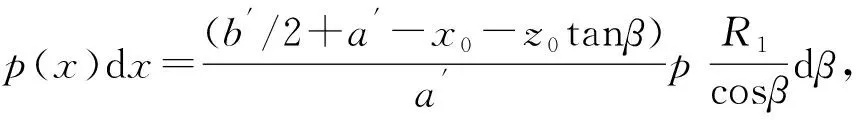
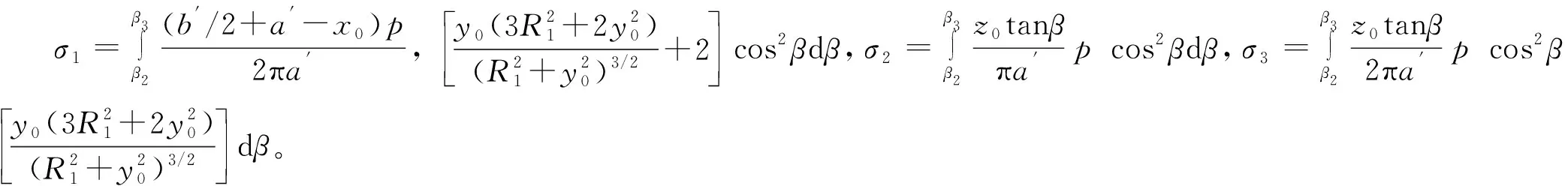
因σ1、σ2与式(18)推导类似，这里直接给出

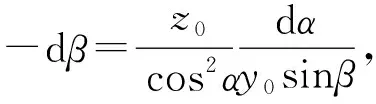
(19)

(3)σz3表达式

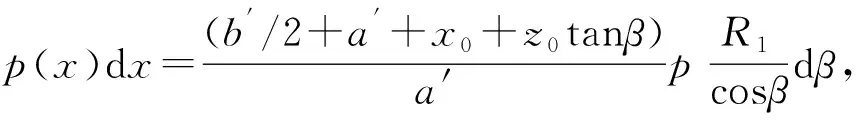
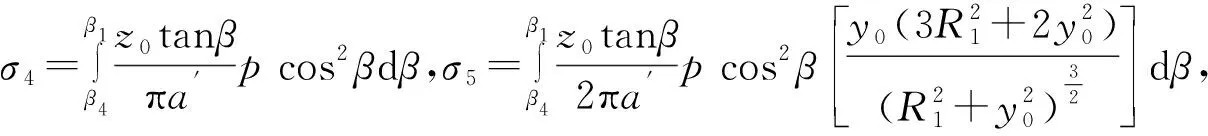
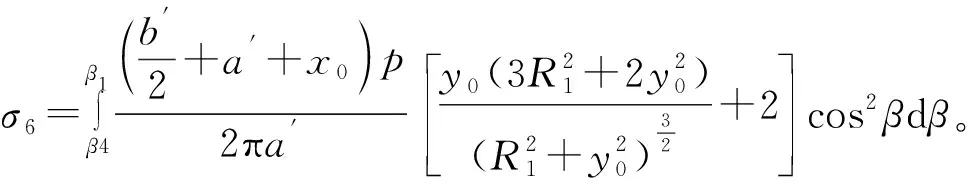
将式(12)代入得到σz3表达式

(20)

式(18)～式(20)中的几何参数表达式汇总如下

i=1,2,3,4

对于以上应力公式的推导，笔者已借助数值模拟对其可靠性进行了验证[11]。值得一提的是，文中附加应力推导是基于更具普适意义的过渡段路基模型进行的，其特点是沿线路走向的范围为[-y0,+∞)，y0为计算点至固定边界(如桥台)的距离。随着计算点距边界距离y0的增加，其附加应力受边界影响越小。通过计算，当y0/h≥3(h为路基填高)时，y0的变化对附加应力不再产生影响，应力计算退化为平面问题，即普通路基的情况。由于篇幅所限，本文研究范围仅限普通路基，计算时取y0=4h。

1.4 工后沉降计算

目前，确定压缩层厚度主要有三种方法：应力比法、应变比法及基底宽度比法。文献[13]中推荐采用应力比法(0.1法)来确定路基荷载下地基压缩层厚度，即当某一深度土层的附加应力小于或等于0.1倍的自重应力时，地基压缩层即取至该土层底面位置。

在施工现场路基的填筑往往分级进行。假定路基多级堆载下地基土的变形满足Boltzmann叠加原理[14-15]，则地基土在任意时刻t的蠕变应变ε(t)即为前期每一级荷载增量Δσi产生的在这一时刻t的蠕变应变εi(t)之和，即ε(t)可表示为

ε(t)=∑εi(t)=∑ΔσiJ(t-ti)t>ti

(21)

式中：J为材料函数。

综上所述，计算思路为：首先采用Mesri蠕变模型计算路基填筑某一阶段的土体蠕变应变，再由Boltzmann叠加原理实现路基多级堆载下地基土蠕变应变的累积，最后再给定地基压缩层厚度Δz和压缩层划分总层数n，则可得到路基多级堆载下地基面在第i阶段的长期沉降

(22)

式中：εik(t)为t时刻第k层地基土在第i阶段的蠕变应变，由式( 8 )计算求得；n为由应力比法确定的地基压缩层分层总数。本文将路基施工填筑过程简化为四级加载，当m=1时，表示路基第一次堆载阶段，t∈[0,T1] ，T1为第二级荷载填筑开始时刻；当m=2时，表示路基第二次堆载阶段，t∈[T1,T2]，T2为第三级荷载填筑开始时刻；当m=3时，表示路基第三次堆载阶段，t∈[T2,T3]，T3为轨道板开始铺设时刻；当m=4时，表示路基轨道铺设阶段，t∈[T3,T4]，T4为轨道板铺设完成时刻；当m=5时，表示路基工后阶段，t∈[T4,+∞)。整个路基填筑过程可以由图4来简化描述。

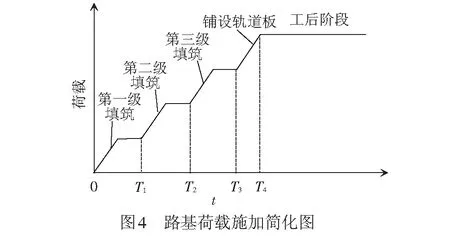
路基工后沉降等于路基施工完成后(运营阶段)某一时刻的总沉降与铺轨工作结束时刻的路基沉降的差值，即Sp可表示为

Sp=S5(t)-S4(T4)

(23)

2 试验验证分析

依托中等压缩性土地基沉降特性及加固技术研究项目[16]，对本文方法的可行性进行验证。试验土样取自胶济线客运专线现场原状土样，其物理力学指标见表1。通过GDS三轴室内试验得模型地基土强度指标：c= 20.8 kPa，φ= 30.7°，k0= 0.61。

表1 土体基本物理力学性质指标

为了得到地基土Mesri蠕变模型参数，对粉质黏土试样进行流变试验，试验过程采用分级加载方式下三轴应力应变状态的排水蠕变。试验尺寸为：直径61.8 mm、高度150 mm，蠕变加载持续时间为15 d。由试验结果得到Mesri蠕变模型参数

2/(Eu/Su)=0.036 8Rf=0.847

(24)

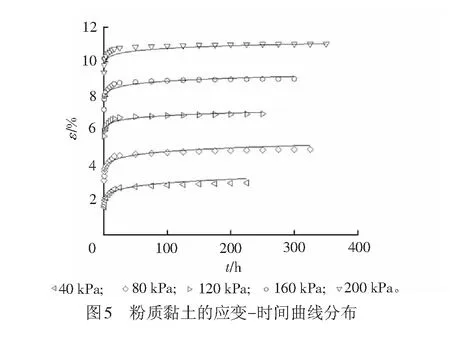
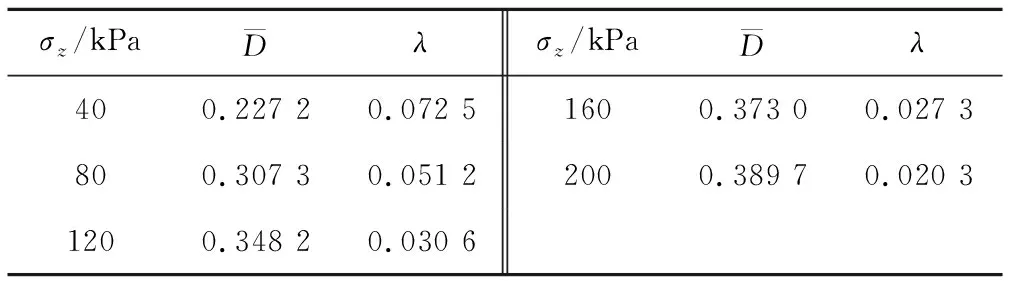
表2 不同剪应力水平下的λ值

由于离心模型试验能够还原原型地基自重应力水平且能很好地控制边界条件及地基土物理力学参数，本文用以验证沉降计算方法。试验模型率n=80，地基土为取至现场的粉质黏土，以强度指标(c、φ值)为主要控制条件对土体进行重塑，然后在模型箱中分层填筑，总厚度为35 cm(对应原型为25 m)。模型路基采用黄土质粉质黏土制作，在预制的模具中以设计压实度分层压实。路基成型后再将其安放在模型地基面的设计位置。模型路基高度为9.4 cm(7.5 m)，底部宽度为37.8 cm(30.2 m)，坡率m=1∶1.5，填土重度为20 kN/m3。路基的填筑过程采用变加速度法来模拟，加速度分别为20g、40g、60g、80g，对应路基的填高为1.9、3.8、5.6、7.5 m。然后维持80g加速度4.5 h，模拟工后40个月的时间。试验过程中借助沉降板来监测路基中心下地基面的沉降，图6为离心模型试验照片。

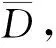
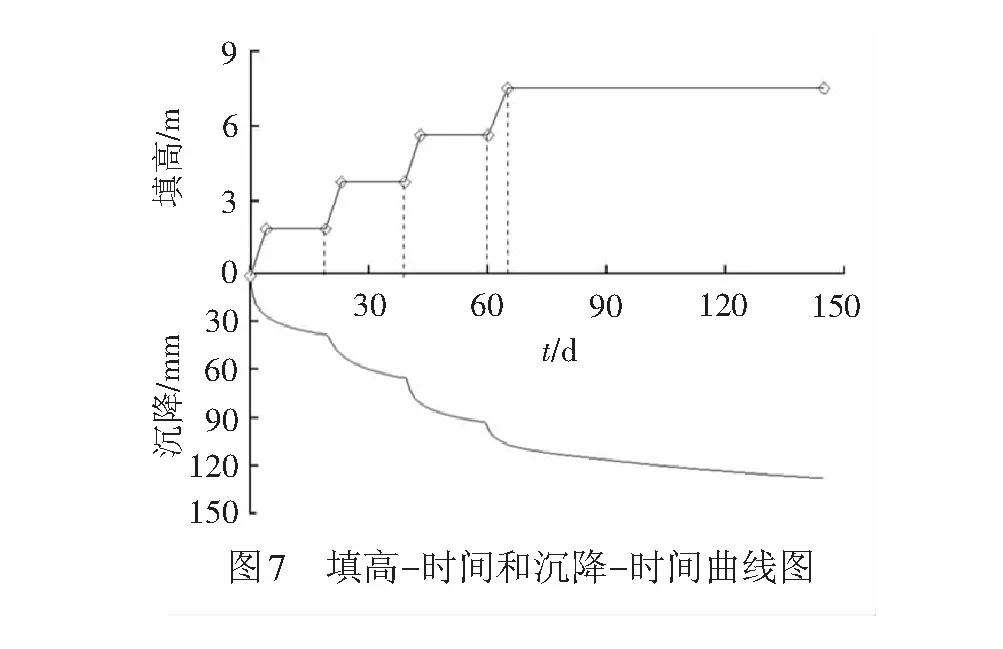
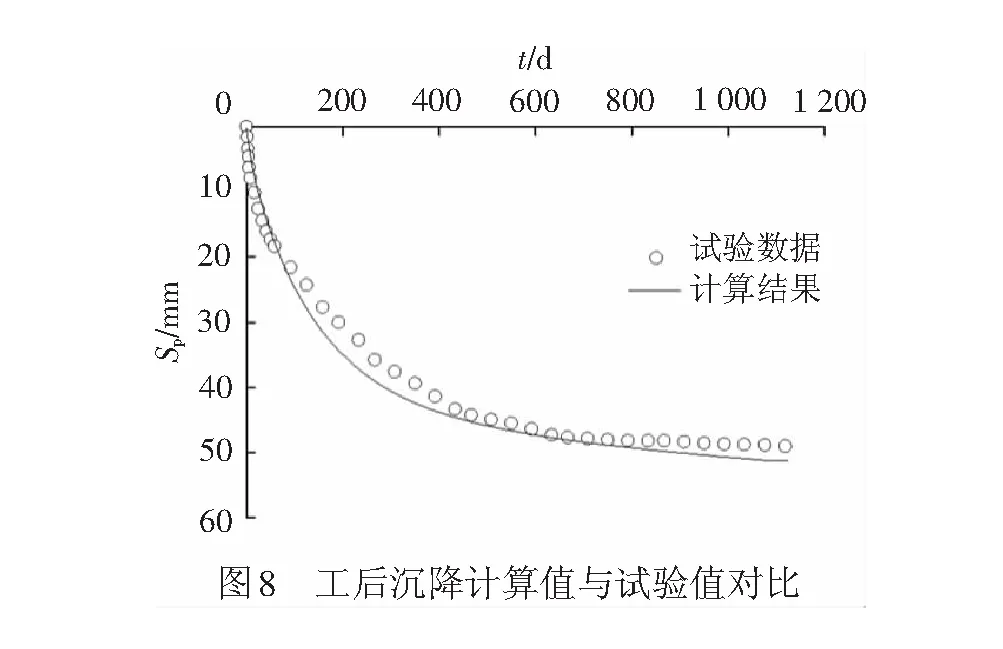
基于以上计算结果，由式(23)便可得到路基工后沉降，将其与离心模型试验进行对比，见图8。从图8可以看出，计算的路基工后沉降大小及变化趋势均与离心模型试验结果基本吻合，计算结果精度较高，在100～400 d范围内，计算值大于实测值，最大的相对误差不超过13%，到800 d以后计算值也略大于试验值，从而验证了式(23)的可行性及可靠性。从沉降趋势可以看出，在铺轨完成后约2 a的时间，沉降速率逐渐变缓，路基沉降开始趋于收敛，此时的沉降值占工后总沉降的80%以上。

3 结束语

从土体流变特性出发，本文将Mesri蠕变模型理论与路基荷载下受路基宽高比影响的附加竖向应力解析式相结合，提出了一种多级堆载下针对天然地基的路基工后沉降计算方法。该方法适用范围广，且具有便于计算机编程、模型参数少、物理意义明确等优点，参数取值可通过常规土体流变试验得到，在实际工程中易于推广。与离心模型试验对比发现，采用本文方法计算得到的路基工后沉降与试验结果吻合较好，且计算精度较高，验证了计算方法的可行性及可靠性。

虽然本文研究成果适用范围为天然地基，然而仍具有一定工程意义。一方面，可就路基堆载下天然地基是否满足工后沉降要求作出定量判断；另一方面，通过预测天然地基条件下路基工后沉降量及发展趋势，从而更好地指导后续地基处理的设计工作，使得地基处理方案既满足工后沉降要求又经济合理。