基于分形理论的高速铁路高架桥接触网系统雷击空间电场研究

李瑞芳， 陈力生， 陈 奎， 曹晓斌， 孙晓东， 徐 超

(1. 西南交通大学 电气工程学院， 四川 成都 610031; 2. 成都地铁运营有限公司， 四川 成都 610031)

高速铁路运输能力强、运营速度快等优势恰恰满足了我国当下的经济建设需求。保障高速铁路安全、正点运行成为现今的主要任务之一。国内高速铁路的运行情况表明，多条高速铁路线路自开通以来均发生过雷击故障，如合武线、福夏线等[1]，其中“7.23甬温线特别重大交通事故”造成了大量的经济损失和人员伤亡[2]。雷击严重影响了高速铁路的安全、正点运行，因此高速铁路防雷成为目前的一个研究重点。

世界上高速铁路发达的国家如法国、德国和日本的地形、地貌和气候条件与我国不同，我国在高速铁路设计中又大量采用了高架桥，大多数线路的桥梁比例超过50%，远超其他发达国家[3]，国外高速铁路的防雷研究成果将不适用于我国。为了研究出符合我国实际情况的高速铁路防雷措施，国内学者经过长期努力取得了一定的成果。国家电网陈维江教授等基于高架桥的实际参数建立了高速铁路接触网雷电过电压的计算模型，评估了接触网雷电防护性能[4]；国网电力科学研究院的谷山强教授等建立了高速铁路供电系统雷电过电压分析模型，评估了接触网的雷电屏蔽防护性能[5]；西南交通大学吴广宁教授等建立了高速铁路接触网的先导通道传播模型，计算了直击雷和感应雷的引雷范围，研究了雷电流幅值和高架桥高度对引雷范围的影响，分析了高速铁路接触网的引雷特性[1]；西南交通大学的周利军教授等分析了现有高速铁路防雷体系的缺陷，研究了高速铁路牵引供电系统的雷击特性[6]。上述研究应用的雷击模型有2种：电气几何模型(EGM)[7-9]和先导传播模型(LPM)[10-11]。电气几何模型用与雷电流幅值相关的击距参数从几何的角度分析线路的屏蔽性能，极大简化了雷击过程，但无法考虑雷电发展的随机性，在精确性和适用性上存在不足之处。先导传播模型克服了电气几何模型不能考虑运行电压影响的不足，更加符合雷电先导发展的物理过程，但该模型只考虑了先导发展的确定性，将下行先导的发展方向设置为先导前方场强最大的方向，未考虑雷电先导发展的随机性。

分形理论从20世纪90年代起开始被一些学者应用于模拟雷电的发展过程，结合绝缘击穿模型(DBM)[12]，形成了兼顾雷电先导发展过程中的确定性和随机性的分形发展模型[13-14]，较EGM模型和LPM模型更加精确地描述了雷电发展过程。目前国内外尚无学者应用分型发展模型进行高速铁路的防雷研究，分形发展模型为高速铁路的防雷研究工作提供了一个新的思路。本文尝试建立高速铁路高架桥接触网系统的雷击分形发展模型，模拟雷击高速铁路高架桥接触网系统的全过程，详细分析了雷电跃变前一瞬间的空间电场，得出了接触线和AF线的工作电压、高架桥高度和雷电流幅值对该空间电场的影响，为进一步研究高速铁路的防雷提供了一定的理论基础。

1 建模理论及模型参数

1.1 分形发展模型下的雷击过程

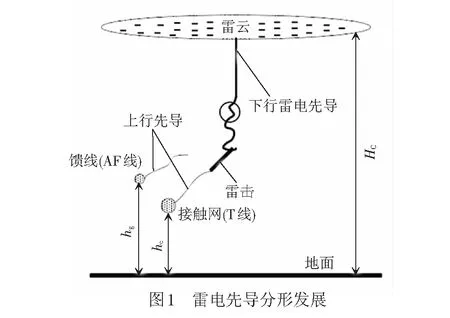
随着雷云电荷积累，雷云下表面某个位置的场强超过下行先导起始的临界场强时，下行先导起始。当下行先导附近的场强满足下行先导发展条件时，下行先导逐级向下发展，不断影响空间电场，使得空间电场动态变化。在下行先导的发展过程中，导线表面的场强可能超过上行先导的起始场强，上行先导在此时产生并逐渐向上发展。上、下行先导之间或下行先导和地物之间的平均场强超过跃变所需平均场强时，上下行先导或下行先导和地物连接，此时雷击发生。

分形发展模型将此连续发展的过程离散为多步发展的过程，给定研究空间，在空间上表面设置起始下行先导，通过计算空间电场来判断有无上行先导起始和确定上下行先导的下一步发展点，若有上行先导起始，上下行先导按照一定的速率比并兼顾确定性和随机性进行发展，直至上下行先导或下行先导和地物连接，此时发生雷击，见图1。在超、特高压输电线路防雷中，输电线路的电压等级高，线路半径大，架设输电线路的塔高度在40～60 m之间，容易产生上行先导，上行先导的影响不可忽略[13]。而在铁路防雷中，线路电压等级为27.5 kV，线路半径在10 mm以下，高架桥高度小于20 m，远达不到输电线路的水平，上行先导的影响不大，因此本文不考虑上行先导的影响。

1.2 空间电场计算

雷电发展过程中任意时刻的空间电场由该时刻的雷云电荷分布、先导通道电荷分布和地物感应电荷分布三部分共同决定。本文中的地物感应电荷分布为大地、高架桥及其他地物所产生的感应电荷分布。由于整个空间电场是一个极其复杂的动态过程，为了将复杂过程模型化，必须适当简化该过程。分形发展模型将雷击过程离散为多步发展的过程，每步之间的时间非常短，在这一极短时间内，空间中的电荷分布视为不变，则整个空间电场为准静态场[15-16]，因此本文采用有限差分法计算每步电场[17]。

雷云一般在2 500 m高空，如果将2 500 m长宽高的三维空间作为研究对象，会使计算量非常大，消耗过多的计算时间，而本文的研究是以高速铁路高架桥接触网系统为前提进行的，因此只需选择高架桥附近足够大的空间作为研究空间。目前三维雷电分形模型尚存在一些不足，因为自然界中所观测到的闪电都是闪电的三维路径在某个二维观测面上的投影，其分形统计特性也是基于该观测结果得出，三维路径的统计特性由于三维图像数据难以获取尚缺乏理论依据，因此根据高架桥自身的对称结构本文选择某个垂直于高架桥桥面的二维空间作为研究空间。综上所述，本文选择300 m长宽的二维空间作为研究空间，高架桥位于x轴的中间位置，见图2。

将所选研究空间划分为300个1 m长宽的小网格。准静态场的空间电势满足泊松方程

( 1 )

式中:φ为电势;x、y分别为图2中的横坐标和纵坐标。

空间的左和右边界满足Neumann边界条件，上边界满足Dirichlet边界条件并根据雷电流幅值按照文献[15]1820中雷电流幅值与等效雷云电位的关系给出等效雷云电位。放电通道、空间的下边界、高架桥桥身及牵引网也作为Dirichlet边界条件，其电位值是固定的。在网格划分的基础上将式( 1 )用差分形式表示为

4φi,j-φi+1,j-φi-1,j-φi,j+1-φi,j-1=0

( 2 )

式中：φi,j为横坐标为i、纵坐标为j的点电势值，V。

整个空间的电势构成一个大型稀疏方程组

Aφ=0

( 3 )

式中：A为系数矩阵；φ=(φ1,1,φ2,1,…,φN,1,φ1,2,φ2,2,…,φN,2,…,φ1,N,φ2,N,…,φN,N)T。

采用SOR迭代法求解，将式( 2 )改写为迭代格式，即

( 4 )

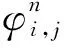
( 5 )

式中：J为Aφ=0的Jacobi迭代格式的迭代矩阵；ρ(J)为J的谱半径。

计算得出ωopt=1.979 273 5。

1.3 先导分形发展规则

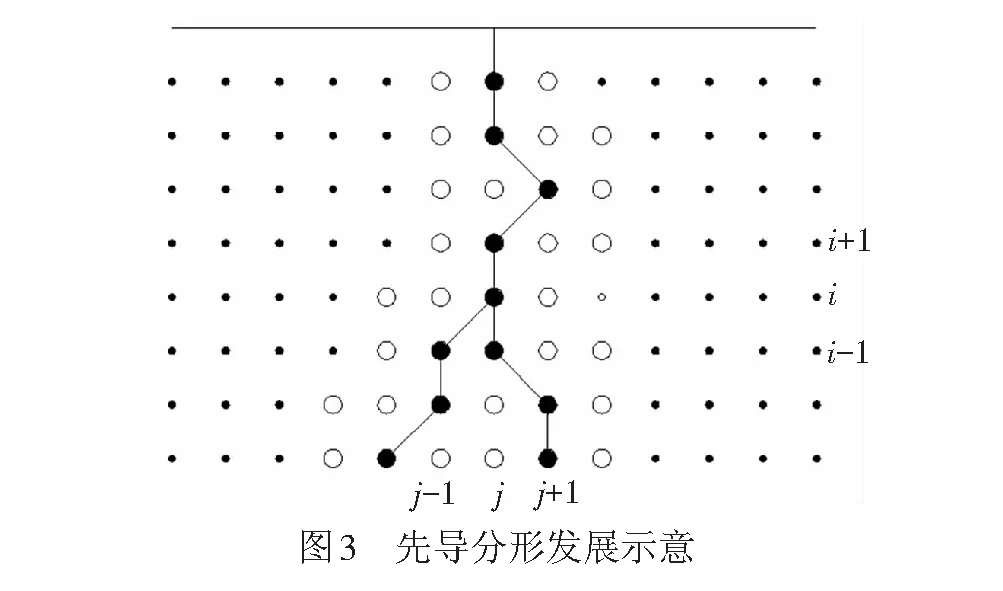
自然界中的雷电在发展过程中呈现多分支现象，分叉明显，分形发展模型正是应用分形几何学来尽可能准确地描述这一发展过程，分形过程见图3。下行先导从上边界起始，大的黑点为先导通道的已发展点，由黑色实线连接。先导每步发展一个大的黑点，每个大的黑点周围距该黑点给定发展步长的点(对应图中的空心圆圈)若满足式( 6 )所述的条件就可能成为先导的下个发展点，而这些可能的发展点的发展概率满足式(7)的约束，由其附近的局部场强决定[18-19]。

( 6 )

式中：E为已发展点与距其给定发展步长的点之间的平均场强大小，V/m；φi,j-φi′,j′为这两点的电势差，其中φi,j为已发展点的电势，φi′,j′为未发展点的电势，V；L为这2点间的距离，m；Ec为放电临界场强大小，kV/m，Ec=216 kV/m。

( 7 )

式中：P((i,j)→(i′,j′))为先导从点(i,j)往点(i′,j′)发展的概率值；η为发展概率指数。

式( 6 )、式( 7 )表明，当先导已发展点与距其给定发展步长的点之间的平均场强大小大于放电临界场强大小时，给定发展步长的这些点将可能成为先导的下一个发展点，每个可能发展点的发展概率由其附近的局部场强决定并与发展概率指数η有关。局部场强体现了先导发展的确定性，发展概率指数体现了先导发展的随机性并且起到了协调确定性和随机性的作用，η越小先导发展与电场分布越不相关，η越大先导越倾向于往电场最大的方向发展，考虑先导分形发展的确定性和随机性，η必须取合适的值。

不同的η值会使模型的分形维数不同。为了使分形模型更接近实际中的雷电发展情况，需选择η值使得模型的分形维数符合实际中雷电的分形维数。至今已有不少学者对实际雷电进行了观测并计算出了其分形维数[20-21]。何金良、司马文霞等通过将这些测量结果与模型的分形维数对比给出了η的取值范围[13,15]。综合考虑，本文采用文献[22]中η的取值，取值为1。

1.4 跃变判据

雷电上行先导和下行先导末端的流注很近或下行先导末端流注靠近地面物体时，若对于未击穿的空气间隙满足一定条件，雷电先导发展速度就会快速增加，并且按照近似直线的路径向雷击物发展，此时将会出现雷电最后一跳击穿的现象，该现象称之为跃变。本文选用的雷电最终跃变判据为：雷电的下行先导通道头部与产生的迎面上行先导通道顶端或未形成上行先导的线路、地面建筑物和大地之间的平均场强大于空间临界跃变击穿场强时发生跃变。本文中的空间临界跃变击穿场强取500 kV/m[23]。

2 模型建立及验证

2.1 高架桥模型

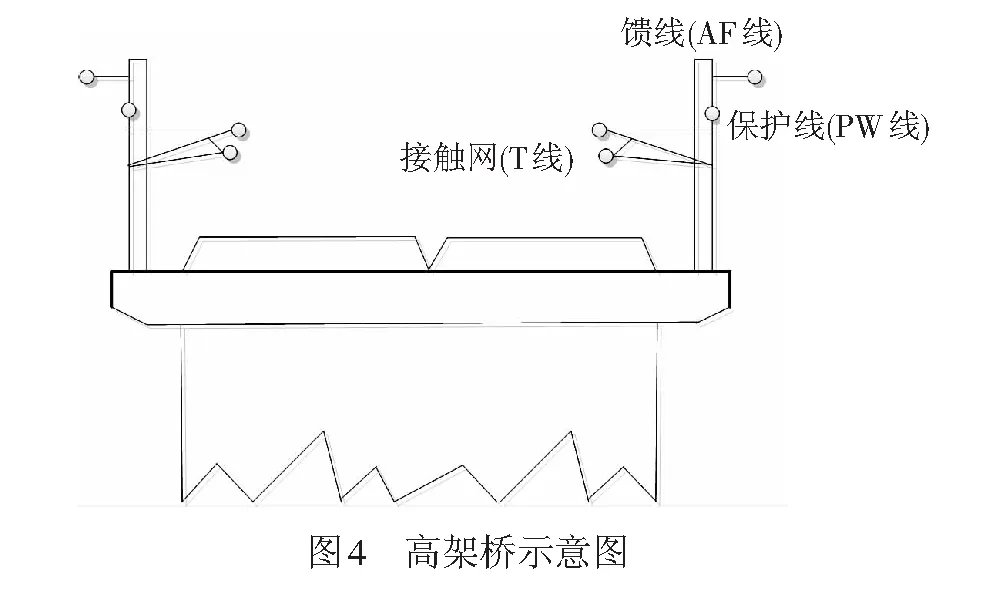
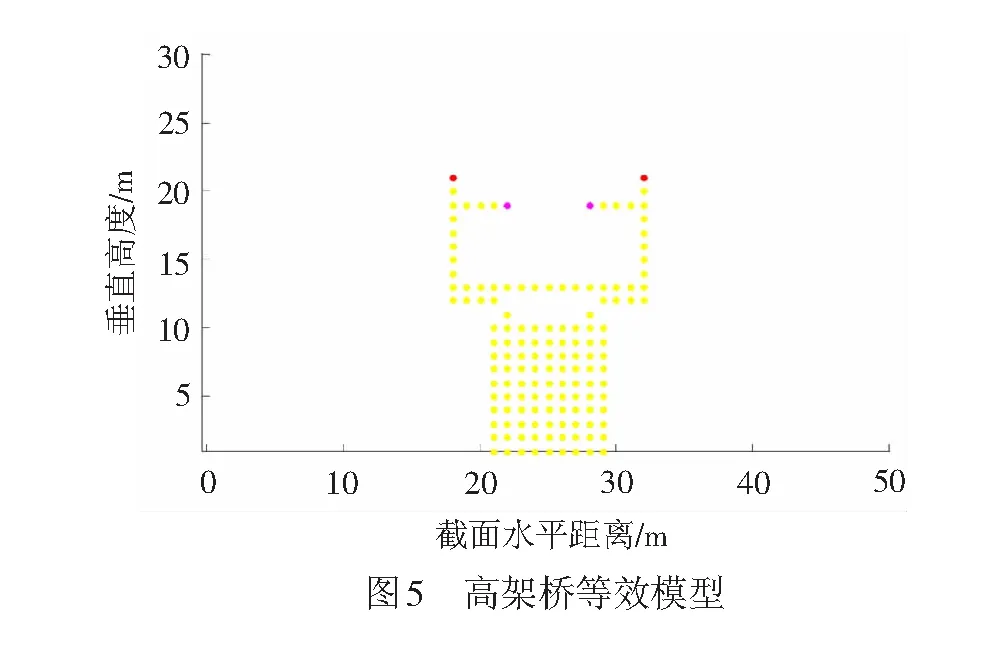
高架桥结构见图4。高架桥参数为：接触线、AF线和保护线距桥面的高度分别为5.3、7.4、6.9 m。高架桥的箱梁下表面宽为6.7 m，上表面宽为14.3 m，高为3 m。高架桥的桥墩高为9 m，宽为7. 6m。接触线和AF线的工作电压分别为27.5 kV和-27.5 kV，保护线上的运行电压近似为零。桥墩和箱梁通过其内部的接地钢筋与大地相连，等效为零电位。支柱与箱梁相连，也等效为零电位。将上述模型等效为图5所示的模型。支柱、桥墩和箱梁等效为图中黄色的点；AF线等效为图中红色的点；接触线等效为图中粉色的点。

2.2 分形发展及空间电场计算模型

本文的雷电分形发展及空间电场计算流程见图6，计算跃变前一瞬间的空间电场。先导的电位随先导的发展不断变化，通常越接近地面其电位越低[24]，因此先导发展到距离地面很近时可以视作常数，Mazur等也正是由于这个原因将其研究中的雷电通道电位设置为常数[25]。本文中的空间仅为300 m长宽，与2 500 m雷云高度相比可以视作非常接近地面的情况，因此本文将先导通道电位设置为常数，作为Dirichlet边界条件。将先导发展步长设为小于一个雷电梯级长度即可达到仿真雷电先导路径准确度的要求，减小仿真步长虽然可以提高精度，但计算量会增加，所需的时间也会随之增加，本文综合考虑时间和精度的要求，将先导发展步长设置为3 m。

2.3 模型验证及结果分析

本文通过多次相同条件下的仿真得到先导的分形发展规律。

图7为其中的2次仿真结果。仿真结果显示，相同条件下的多次仿真得到的分形发展路径并不相同，并且出现多级分叉现象，越接近地面分叉现象越明显[26]，符合雷电先导分形发展的随机性。从图7中所画的等差值电势线可以看出空间场强分布的基本规律，线越密集的地方电场强度越大，可见雷电先导、高架桥及高架桥上的AF线和接触线使空间电场畸变，在接近地面的空间及先导多个分支的头部产生了极强的空间电场，先导整体的发展趋势为向场强最大的方向发展，符合雷电先导分形发展的确定性。

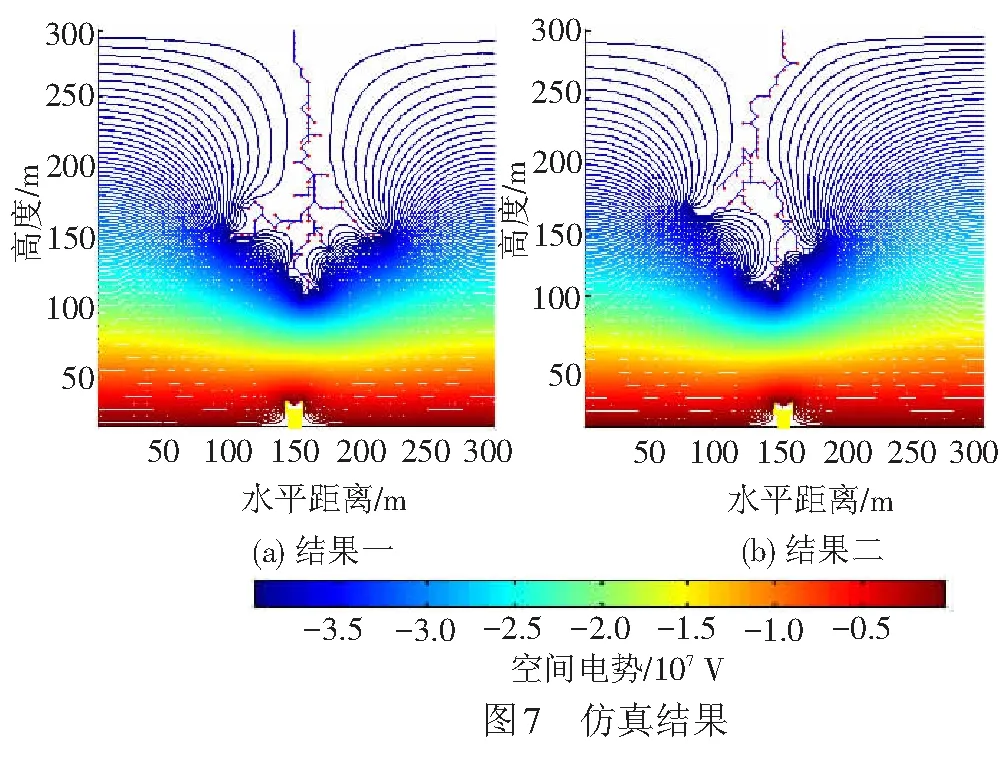
图7中先导的发展最开始没有明显的指向性，随着先导的逐渐发展，空间电场出现上述的畸变现象，某个先导分支的头部与高架桥之间的场强逐渐增加，当该场强增加到一定程度时，先导的发展开始出现指向性，整体上向着高架桥发展，说明高架桥具有一定的引雷作用，并且在仿真结果中大部分的雷电都击中了高速铁路高架桥接触网系统的AF线，原因在于高架桥增加了AF线的高度使得AF线的引雷范围变大，与文献[1]的研究结果一致。

3 空间电场的影响因素研究

3.1 接触线和AF线工作电压的影响

我国高速铁路的牵引供电系统采用AT供电方式，接触线和AF线上分别存在27.5 kV和-27.5 kV的工作电压，其产生的电场是影响整个空间电场的因素之一，影响雷电先导分形发展的路径和最后的跃变。因此，本文分析了高速铁路牵引供电系统中接触线和AF线的工作电压对空间电场的影响，分别按照有无工作电压的2种情况对比分析该工作电压对空间电场的影响。接触线和AF线上有无工作电压的空间电场分布见图8。

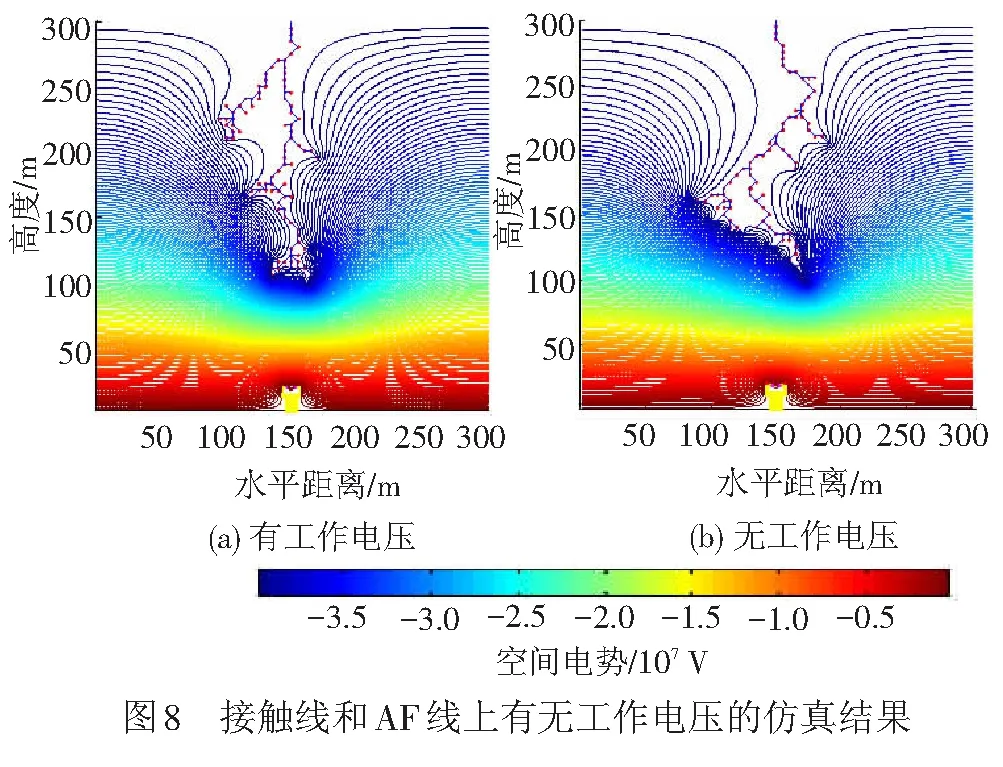
对比图8发现：2种情况下雷电最终跃变高度没有明显差别，均约为100 m，这是由于接触线及AF线产生的电场强度并不大，对空间电场强度的数量级几乎没有影响，因此场强最终达到跃变判据时的跃变高度几乎不变。2种情况下地面附近的空间电场分布几乎一致，但先导附近的强场区以及低于跃变高度空间的空间电场分布有不同特点，接触线和AF线上有工作电压时，先导附近的强场区分布更加集中，和低于跃变高度空间的空间电场一起关于x=150 m的纵轴呈现更加对称的分布，这是由于接触线和AF线上的工作电压产生的电场影响了雷电先导分形发展过程中的电场分布，先导发展到约为200 m高度时就开始出现明显的指向性，先导分形发展的确定性较随机性开始占主导地位，整体趋向高架桥方向发展，较接触线和AF线上无工作电压时约175 m才开始出现该指向性而言，出现指向性的高度高了约25 m。

3.2 高速铁路高架桥高度的影响

本文中高架桥高度指高架桥桥面距离地面的高度。高速铁路高架桥的高度不同对雷电分形发展过程的空间电场影响可能不同。因此，本文分析了高架桥高度对雷电先导分形发展过程的空间电场的影响。分别取高架桥高度为0、5、12、20和30 m进行仿真。高架桥高度对该空间电场的影响见图9。

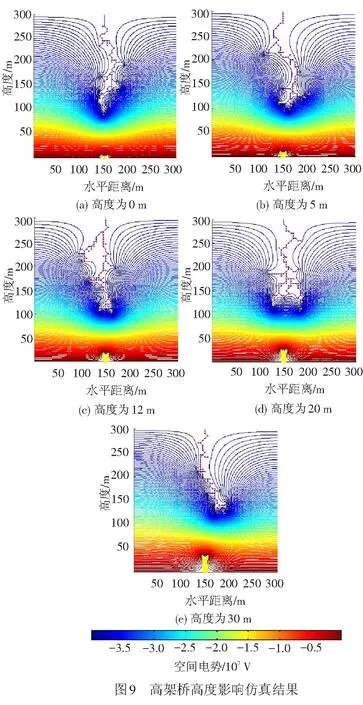
对比图9得到不同高架桥高度下的跃变高度和明显指向性发展高度，见表1。

表1 不同高架桥高度下的2个主要参数

由表1可见，雷电跃变高度和明显指向性发展高度随高架桥高度的增加而增加。这是由于不同高度的高架桥附近的空间电场也不同，高架桥高度的变化导致高架桥几何形态的变化从而改变了边界条件，影响其附近的空间电场分布。高架桥高度越高影响空间电场的范围越大，高架桥与雷电先导头部间的空间电场畸变程度越大，雷电先导发展至更高的高度就已满足跃变判据而发生最后的跃变，先导与高架桥之间的场强也在更高的高度达到一定数值使先导分形发展的确定性较随机性占主导地位，先导整体向高架桥方向发展。可见高架桥高度越高越易遭受雷击。从图9(d)、图9(e)可知，由于分形发展的随机性，先导发展路径也可能在出现明显指向性发展后，出现多条分支同时按照该指向性方向发展或再次偏离该指向性发展方向的现象。

3.3 雷电流幅值的影响

雷电流幅值直接影响了雷电先导分形发展过程的空间电场。本文分析了雷电流幅值对雷电先导分形过程空间电场分布的影响。为了便于将雷电流幅值转化为等效雷云电位，研究不同等级的雷电流幅值对空间电场的影响，分别取雷电流幅值为45、135和225 kA进行仿真，其对应的300 m高度的等效雷云电位分别为-40、-120和-200 MV。仿真结果见图10。

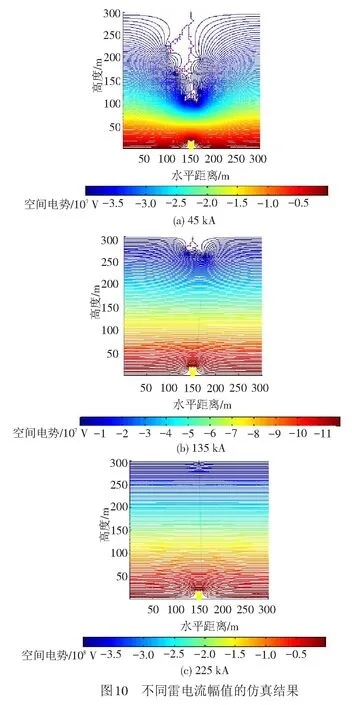
对比图10发现：雷电先导分形发展最终的跃变高度随雷电流幅值的增大而增大，图10的跃变高度依次为100、250和300 m，其中图10(c)的跃变高度因受到研究空间的限制，先导在上边界起始时就满足跃变条件从而直接跃变，即雷电流幅值为225 kA时的跃变高度是大于300 m的，这是由于雷电流幅值对空间电场强度的数量级影响很大，从而直接影响了雷电最终的跃变高度，更大的雷电流幅值使得雷电先导分形发展到更高的高度时就已满足跃变条件；图10的空间电场分布随雷电流幅值的增大而变得越均匀，这是由于雷电流幅值增大导致跃变高度增大，从而使得雷电先导的分形次数减少，先导通道对空间电场的畸变作用减小，背景电场的影响相对增大，即雷电流幅值越大，击穿前一瞬间跃变高度以下的空间电场会更加均匀。

4 结论

本文基于雷电分形发展的统计特性搭建并验证了高速铁路高架桥接触网系统引雷的分形发展模型，通过该模型研究了接触线和AF线工作电压、高架桥高度以及雷电流幅值对高速铁路高架桥接触网系统雷击空间电场的影响，得到如下结论：

(1) 接触线和AF线的工作电压对空间电场强度的数量级几乎没有影响，场强最终达到跃变判据时的跃变高度几乎不变。但该工作电压对空间电场的分布有一定影响，先导分形发展出现明显指向性的高度略微增加，先导附近的强场区分布更加集中，和低于跃变高度的空间电场一起关于x=150 m的纵轴呈现更加对称的分布。

(2) 高架桥高度对空间电场分布有一定影响，高架桥高度越高，畸变其附近电场的作用范围越大，高架桥与雷电先导头部间的空间电场畸变程度越大，从而使得雷电的跃变高度越高，雷电先导分形发展出现明显指向性的高度也越高。但由于分形发展的随机性，先导发展路径也可能在出现指向性发展后出现多条分支同时按照该指向性方向发展或再次偏离该指向性发展方向的现象。

(3) 雷电流幅值对空间电场的场强数量级和分布都有一定影响。雷电流幅值增大使得空间场强的数量级增大，从而导致跃变高度增加。而跃变高度增加使得先导分形发展的分形次数减少，即先导通道对空间电场的畸变影响将会减小，背景电场的影响相对增大，使得击穿前一瞬间跃变高度以下的空间电场分布更加均匀。