受电弓降弓过程弓网电弧等离子体动态特性研究

郝 静， 高国强

(西南交通大学 电气工程学院， 四川 成都 610031)

弓网系统作为列车重要的取流设备，其良好的服役性是保障列车安全运行的重要条件。动车组运行过程中，升降弓操作、车体震动、接触网导线和轨道不平顺等因素致使弓网电弧现象频发。一方面其产生的高温和过电压对列车运行安全[1-2]和受电弓滑板寿命造成严重的威胁[3]；另一方面由于弓网电弧具有续流作用，对其不能简单采取灭弧措施。因此，有必要对弓网电弧的物理电气特性进行研究。

早期对弓网电弧的研究主要集中于对电弧的电气特性和图像特性的研究，但现场实验不仅危险性高、难度大、耗资大，且难以获得电弧内部参数信息[4-5]。计算机技术和磁流体动力学的发展，使得采用数值仿真研究电弧成为可能。数值计算方法在开关电弧的研究中得到了广泛应用，许多学者仿真研究了开关触头打开过程中电弧的发展过程[6]、电弧过栅片的分裂过程[7],以及电弧在跑弧轨道的运动过程[8]。对于弓网电弧，文献[9-10]研究了不同电流和不同弓网间隙下电弧的静态特性。而在受电弓降弓过程中，随着弓网间隙连续性地增大，受电弓与接触网附近气流场发生明显变化，其对电弧特性的影响是不可忽略的[11-12]。将受电弓运动过程与电弧变化过程联合仿真，能更真实地仿真降弓过程电弧的动态特性。

本文基于磁流体动力学理论，建立弓网电弧仿真模型。对Fluent流体软件进行二次开发并将其作为求解平台，利用Fluent动网格技术，不断更新受电弓运动过程中求解区域内网格，仿真计算出受电弓降弓过程中温度场和气流场分布，分析气流场在降弓过程中对电弧特性的影响。分别对降弓速度0.2、0.5、1.0 m/s时的电弧特性进行仿真，分析降弓速度对电弧弧柱电压的影响规律。利用弓网系统模拟试验平台测试降弓过程中电弧电压的变化规律，对比分析试验电弧电压与仿真电弧电压。

1 计算模型

1.1 弓网电弧仿真几何模型及仿真假设

针对受电弓降弓过程，沿垂直于列车运行方向建立弓网电弧仿真几何模型，接触网导线几何尺寸与实际尺寸一致,半径为6.5 mm。由于远离电弧的受电弓滑板两侧对电弧特性影响很小，为减小计算量，模型中受电弓尺寸小于实际尺寸。图1为弓网系统，受电弓以速度V沿y轴负方向运动。为求解磁场和减小回流对计算结果的影响，模型中将空气求解区域扩展至弓网系统的2～3倍，由于篇幅限制，空气扩展部分未在图中给出。

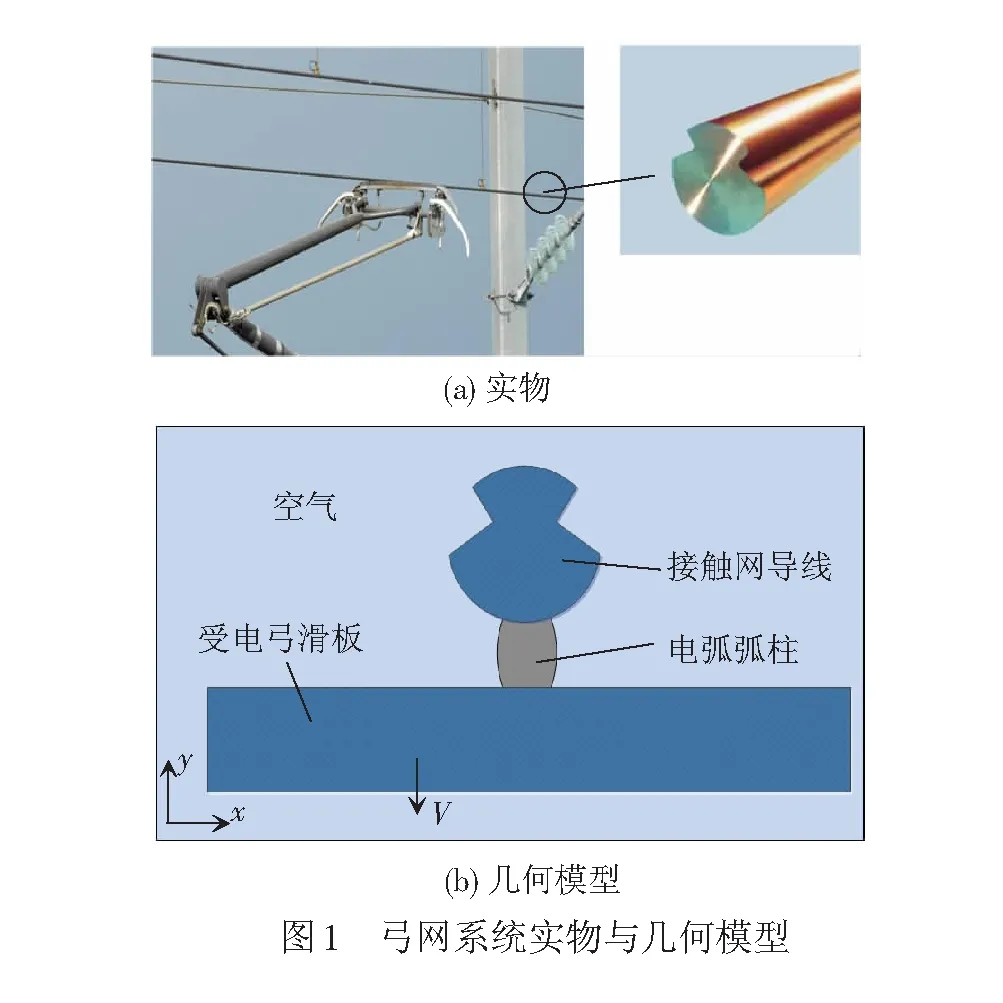
受电弓降弓过程中电弧的变化是复杂的电磁过程，为简化运算，本文在仿真中作如下假设：

(1) 不考虑电弧的产生过程，即在仿真计算开始时，弓网间隙间已存在稳定的电弧。

(2) 不考虑电弧高温导致的电极材料发生的相变过程以及金属蒸汽对电弧特性的影响。

(3) 求解区域的电弧等离子体为层流，处于局部热平衡状态，仿真过程中不考虑电极附近非局部平衡状态的鞘层[13]。

(4) 在电弧与电极之间存在能量交换过程，一方面，电弧将热量传递到电极，另一方面，电流流过受电弓滑板和接触网导线产生的焦耳热将部分传递到电弧。为减小仿真复杂程度，不考虑电极和电弧之间的能量传递过程。

(5) 受电弓在降弓过程中做变速运动，由于燃弧间隙很短，在对电弧特性仿真时，将其视为匀速运动。

1.2 控制方程

在研究电弧等离子体时，常将其视为带电流体，该物性参数包括密度、黏性系数、电导率和热导率等，它们是温度和压力的函数。电弧等离子体内部存在热场、电磁场和气流场相互作用的复杂过程。计算初始，根据初始压力和温度分布，得到物性参数值，由电导率和边界条件根据麦克斯韦方程组得到电位和电流密度分布。一方面，电流产生的焦耳热使电弧温度升高，另一方面，电弧高温区向外辐射和对流热量。与此同时，电弧在磁场的作用下运动，使压力和温度值发生变化，影响电导率、热导率和密度等物性参数。

电弧的求解依托于磁流体动力学，包括流体动力学的Navier-Stokes方程组、求解电磁场的Maxwell方程组和Biot-Savart方程。其中，Navier-Stokes方程组包括质量、动量和能量守恒方程。为描述焦耳热对电弧的加热作用、辐射的冷却作用以及电磁力作用，分别给能量方程和动量方程加入能量源项和动量源项。各方程之间具有强耦合性。

(1) 质量守恒方程

( 1 )

(2) 动量守恒方程

( 2 )

Svi=(J×B)i

( 3 )

(3) 能量守恒方程

( 4 )

( 5 )

式中：ρ为等离子体密度；v为速度矢量；vi为不同坐标方向上的速度分量；η为黏性系数；p为压强；Svi为动量守恒方程源项；J为电流密度；B为磁感应强度；T为温度；λ为热导率；cp为比热；σ为电导率；能量源项ST由黏性耗散项V、焦耳加热项J2/σ和辐射项QR组成。黏性耗散项在能量平衡方程中仅用于能量的重分配并不产生附加热量，因此，在计算中常将此项忽略。由于电弧温度非常高，其热辐射现象明显。难以精确地表达热辐射，因此，本文采用简化公式确定热辐射[14]，即

( 6 )

式中

( 7 )

式中：k为吸收系数；α为玻尔兹曼常数；T、T0分别为电弧温度和环境温度；p0为一个标准大气压。

(4) 电磁场方程

电弧作为导电流体，其内部发生着复杂的电磁场变化。为求解焦耳热和洛伦兹力，须求解场域电场和磁场分布。

根据Maxwell方程组,可得电位φ为

div(σgrad(φ))=0

( 8 )

电流密度为

J=-σgrad(φ)

( 9 )

场域中任何一点rA的磁感应强度可通过Biot-Savart方程求得

(10)

式中:μ0为真空磁导率；dV′为体积微分；rB为电流元矢量；rA-rB为电流元rB到点rA矢量。

1.3 边界条件

由于弓网电弧完全暴露于大气环境中，本文在计算中将空气求解域的边界设为压力出口，压力值为一个大气压，温度设为300 K。对于电场边界条件设置，阴极即接触网导线底面(图2中1)按照Neumann条件即电流密度来定义。然而目前弓网电弧电极表面的电流密度分布难以确定，本文在计算中将阴极表面电流密度假设为一个平均值。阳极即受电弓滑板上表面(图2中2)设置为0电位。对于速度边界条件，将接触网导线和受电弓滑板壁面设为无滑移边界[15]。

1.4 网格更新

在受电弓降弓操作过程中，由于受电弓滑板位置随时间变化，使空气求解区域不断变化。因此，随着计算时间的增加须不断更新求解区域内的网格。计算中将弹性光顺法和局部重构法联合使用对网格进行动态处理，见图2。当受电弓滑板向下移动时，受电弓滑板上部分网格和下部分网格分别被弹性拉伸和弹性压缩，当局部网格的扭曲率或尺寸超过要求规定范围时，此处网格被重构。

2 仿真结果与分析

2.1 电弧温度分布

通过仿真计算得到降弓速度为0.5 m/s时，不同时刻(对应不同间隙l)下电弧温度分布见图3。仿真计算过程中，电流为100 A，计算步长为2 μs。不考虑电弧的产生过程，即初始时刻接触网导线与受电弓滑板之间存在稳定电弧，初始状态弓网间隙为3 mm。

结合本文对气流场的分析可知，受电弓降弓过程中，电弧特性在外部气流场作用下发生显著的变化。当外部气流作用于电弧时，其热损耗增大，为将热损失限制在最小程度以维持燃烧，电弧横截面积收缩。这种在外部气流冷却作用下发生的弧柱横截面收缩现象，称之为热收缩效应[16]。由图3可知，热收缩效应发生于电弧靠近接触网导线区域，且强度随弓网间隙的增大而增大。当弓网间隙从3 mm增大到7 mm时，弧柱低温区收缩，弧心高温区收缩现象不明显，由于弧柱拉长，电弧散热区域增大，电弧最高温度降低。当弓网间隙为8 mm时，电弧形态在外部气流的扰动下发生明显变化,弧柱包括弧心高温区均发生明显的收缩现象，电弧通道变窄，电弧局部区域向两侧扩散,弧柱电流密度增大，热电离程度增大。因此弓网间隙为8 mm时的电弧最高温度相对于弓网间隙为7 mm时有所上升。降弓过程中弧心最高温度随弓网间隙变化如图4所示。由图3还可看到，随着弓网间隙增大，弧柱伸长，弧柱高温区(7 000 K以上)向接触网导线聚集。

2.2 气流场分布

降弓速度为0.5 m/s时，受电弓与接触网导线附近气流场分布见图5。

当受电弓降弓时，由于受电弓位置快速变化，受电弓上部气体压强变小，外部大气与受电弓上部区域存在压强差，气流从外部流向受电弓上部低压区。由于接触网导线的阻碍，气流将绕过接触网导线流向弓网间隙间的低压区，见图5(a)。由于气流与接触网导线壁面间的无滑移条件，气流与接触网导线壁面的相对速度为零，当气流离开接触网导线壁面时，垂直于壁面方向的气流速度迅速增大直至与来流速度相同，表明在接触线表面附近的流场存在速度梯度，速度梯度意味着有黏性应力的存在。在临近接触网导线壁面的摩擦力和黏性力共同作用的薄层区域，称之为边界层[17]。在这个薄层区域以外的气流可不考虑摩擦应力，视为理想流体的势流流动。当雷诺数在一定范围之内时，边界层出现分离，在圆柱后形成两个旋转方向相反的漩涡，如图5(b)和图5(c)。这种现象在流体力学中称之为圆柱绕流[17]，其原理见图6。当漩涡形成后，由于受电弓的阻挡作用，并未向气流下游发展，而是向受电弓滑板两侧发展，气流强度增强，见图5(d)。因此图3中出现电弧温度分布向两侧扩散的现象。

2.3 不同降弓速度下弧柱电压变化规律

根据电导率关于压力和温度的插值数组可得求解域内电导率分布，再通过Maxwell方程组可得电位分布。间隙为3 mm时电位分布见图7。

为研究降弓速度对电弧特性的影响，分别对降弓速度为0.2、0.5、1.0 m/s时的电弧特性进行仿真，其弧柱电压随间隙的变化规律见图8。弧柱电压随间隙的增大而增大，且降弓速度越大，电压变化速率越大。这是由于受电弓降弓速度越大，电弧附近气流场运动越剧烈，电弧热损失越大。由此产生的热损失需以电源输入功率来补偿而保持热平衡，因此输入功率也应增大，在电流恒定不变的情况下，电位梯度增大。

3 电弧电压实验与仿真结果对比

图9为弓网电弧模拟试验装置，接触网导线CW嵌于轮盘W中，在上位机的控制下，伺服电机带动受电弓滑板P垂直方向运动，并可通过调整伺服电机的速度模拟不同的升降弓速度。受电弓滑板与接触网导线在初始时刻接触，在触发信号作用下，受电弓向下运动，示波器采集电压电流波形。

图9中：S为电源; R、L分别为模拟机车负载电阻、电感; W为转盘; CW为接触网导线;V为电压传感器; A为电流传感器;P为受电弓滑板; C为高速摄像机; IPC为工控机。电源电流100 A，降弓速度为0.5 m/s时，实验所得电弧实验电压、电流特性及电弧电压仿真值随弓网间隙变化规律见图10。

由于仿真初始间隙为3 mm，因此电弧电压仿真值始于3 mm处。电弧电压仿真值和实验值均随弓网间隙的增大而增大且变化斜率近似相等。通常将电弧电压近似表达为

Uarc=El+(UA+UK)

(11)

式中：Uarc为电弧电压E为电位梯度；l为电弧长度(由于电弧鞘层厚度非常小，因此弧柱长度近似等于弓网间隙长度)；UA为阳极压降；UK为阴极压降；UA与UK之和称为近极压降。

由于未考虑电极附近非局部平衡状态的鞘层，即未计算近极压降，仿真计算所得电弧电压为弧柱压降。近极压降通常可取10～20 V[18]，对比电弧电压仿真值和实验值，可知仿真结果符合实验结果。

4 结论

(1) 受电弓降弓过程中，弧柱伸长，电弧散热面积增大，弧心最高温度先降低，后在气流作用下发生热收缩效应而升高。同时电弧在外部气流作用下，形态发生显著变化。

(2) 在连续降弓过程中，弓网间由于压强差而产生气流运动，在接触网下方形成2个旋转方向相反的漩涡，该过程称为圆柱绕流。气流的运动对电弧特性有显著的影响。

(3) 受电弓降弓过程中的弧柱电压随弓网间隙的增大而增大，且降弓速度越快，弧柱电压变化率越大。

(4) 将电弧电压实验与仿真值的差值与经验近极电压值对比，验证了仿真模型的可行性。由于在仿真中未考虑电极附近非局部平衡状态的鞘层，使得实验电弧电压与仿真电弧电压间存在差值。因此，模型需进一步完善。