基于改进LSSVM 的一元受电弓弓网接触力建模仿真

黄玉萍，赵 晨，贺文锦

（广东交通职业技术学院 广东 广州 510000）

0 引言

随着电气化铁路的大发展，电力机车已经广泛应用于铁路系统。负责给电力机车输送牵引电能的受电弓与接触网（以下简称弓网）系统，在铁路供电系统中承担着重大任务。弓网受流原理是通过弓头上的滑板与接触线之间连续的电气接触和滑动接触[1]，从而获得电能。因此，弓网之间的接触直接影响列车受流质量。弓网系统通过接触网与受电弓之间的相互接触耦合在一起，弓网动力学行为受到空气阻力、列车速度、接触网波动的传播与反射等影响，因此弓网之间良好的接触是铁路安全可靠运行的重要保障。随着高速铁路信息化、自动化水平的不断提高，铁路运营部门保存了弓网系统大量的离线、在线的实际检测数据，这些数据蕴含了弓网系统丰富的特征和规律信息。因此，探索从既有线弓网实际检测数据建立弓网系统的动力学模型，揭示基于数据的弓网运行规律[2]，对于制定有效的弓网检修计划、选择弓网材料、预测弓网服役寿命等具有直接的现实意义。因此，基于课题组前期开展的地铁弓网系统广义建模仿真，弓网二元受电弓等效模型的建立，本文提出通过一元受电弓等效模型来验证基于改进LSSVM的弓网接触力仿真的有效性和可靠性。

2 弓网系统建模

列车弓网系统是一个连续的时变非线性系统，本节运用子结构方法分析一元等效受电弓的弓网系统耦合动力学方程，并对该方程进行离散化分析，据此进一步构建弓网系统的广义模型。弓网系统是一个相对联系紧密的整体，是通过弓网接触力耦合在一起的复杂动力学系统。弓网包括接触网和受电弓两个子系统，见图1。

接触网是具有一定抗弯刚度的线索结构，由支柱、吊弦、承力索、接触线等组成。受电弓安装在动车顶部，由上框架、下框架、弓头、滑板等组成。

在接触网与受电弓组成的系统中，接触网的刚度在每跨内及跨间不同，可以看作一个时变函数，与列车的运行速度、接触网的类型及参数有关，不同悬挂方式的接触网对应的刚度表达式的参数取值也不一样。把接触网对受电弓的作用简化为一个等效变刚度弹簧，刚度表达式为：

受电弓的数学模型比较复杂，在进行计算机仿真时，通常都要对受电弓单元进行质量归算，归算质量模型是利用动能等效原理将原结构简化成几个具有集总质量的模型。根据等效质量模块数目可以分为一元、二元及多元模型。一元受电弓等效模型见图2。

根据牛顿力学原理，可得图2 所示的接触网单自由度弓网系统动力学方程为：

其中，M为受电弓的等效质量，kg；c为框架阻尼，；s为归算质量模块的垂向位移，m；为静抬升力，N；F表示弓网间接触力，等于等效刚度与垂向位移的乘积，N。

弓网接触力是衡量弓网系统工作性能的重要指标之一，保持弓网接触力在合理的区间内波动是机车获得良好受流的重要条件。因此，研究人员从机械设计、动力学建模、优化控制等多角度对弓网接触力进行了深入研究。其中，建立有效的弓网接触力模型是对弓网系统进行分析、设计、控制、优化的前提和基础。在这一背景下，本文接下来将提出适合于弓网接触力广义模型的非线性建模方法。

式（2）是图2 的弓网系统的连续模型，但现代检测、监控、通信等信息技术在高速列车的广泛应用，使得列车运行过程客观是离散系统[3]，因此需要对弓网连续动力学方程（2）进行离散化。本文采用有限差分法中的二阶差商和一阶前差商的方法来获得弓网连续模型（2）的近似离散化表达式，再进行扩展，构建弓网系统的广义模型。

其中，ai,i=1,2, … ,n是表示弓网位移线性关系的系数，式（3）中的求和项ais(k−i)表示过去时刻的弓网位移对于当前时刻弓网位移的影响。式（3）中θ(k−j),j=0,2, … ,m是(k−j)时刻作用于弓网的因素集合（比如机车速度、接触网间跨距、接触网相邻吊弦间的距离非线性阻尼特性等），g(θ(k−j))表示(k−j)的因素集合对于弓网的非线性作用关系，式（3）中的求和项b jg(θ(k−j))表示当前和过去时刻的因素集合对于弓网位移的非线性影响。式（4）中的ke表示弓网系统受到的随机噪声（由雨雪、大风、列车结构件机械/电气特性变化等引起）。

3 改进LSSVM模型参数辨识

在机器学习领域，核宽度σ、正则化因子γ一般被称为超参数[6]，计算γσ, 通常是一个非线性、非凸的优化问题（即难以得到γσ, 解析表达式），因而采用交叉验证、统计再抽样、单纯形法、智能优化算法(如耦合模拟退火算法CSA、遗传算法)等方法来计算γσ, 。在LSSVM 工具箱中，采用耦合模拟退火法(CSA)和单纯形法（simplex）优化训练得到超参数解γσ, 的初始值，再通过十折交叉验证得到超参数最优解[7]。

求解出弓网广义模型的优化问题（5）—（7）之后，则可利用求解出的模型对弓网未建模的新样本序列θ∗(0),θ∗(1),...,θ∗(m)(由机车速度、接触网间跨距、接触网相邻吊弦间的距离、非线性阻尼特性等组成的因素集合)进行预测，其预测表达式为：

4 试验分析

基于以上分析，本节应用基于改进的弓网模型对simulink 环境下产生的弓网系统数据进行建模仿真预测。根据地铁弓网系统的特点，为了分析弓网结构参数对弓网接触力的影响，利用Matlab 的Simulink 模块搭建弓网系统动力学模型[9]，见图3。仿真中的弓网模型参数为：ho=3 600N/m，M=40kg，L=63m，c=30N·s/m，μ=0.35，静抬升力F=90N。

运行上述Matlab 搭建的弓网仿真模型来近似模拟弓网的动力学行为。实验中分别改变列车运行速度和受电弓等效质量，以分析弓网实验参数对弓网接触力的影响。数值实验产生100 组数据，前80 组数据用来建立上文的弓网广义模型，后20 组数据用来对获得的弓网模型进行预报验证。如4 图所示，为列车速度为100 km/h 时，后20组数据的回归预报结果分析图。

由图4 可知，回归预测数据的相对误差量基本处于±0.025 的范围之内，误差相对较小，说明该方法是有效的，为进一步论证利用弓网实际数据来建模仿真打下坚实的基础。

表1 为不同受电弓等效质量下的接触力变化情况，从左到右共6 列，第1 列是受电弓的等效质量，第2、3、4 列分别是不同等效质量下利用获得的模型预测弓网接触力的最小值、最大值及其变化幅值，第5、6 列分别是每种质量的建模数据对应的LSSVM 框架下弓网广义模型的超参数γσ、 的优化解(γσ、 首先由耦合模拟退火算法和单纯形法优化得到其初始值，再通过十折交叉验证获得其最终结果，与上述第一试验的方法类似)。各组实验弓网接触力的变化情况、超参数等具体信息见表1。

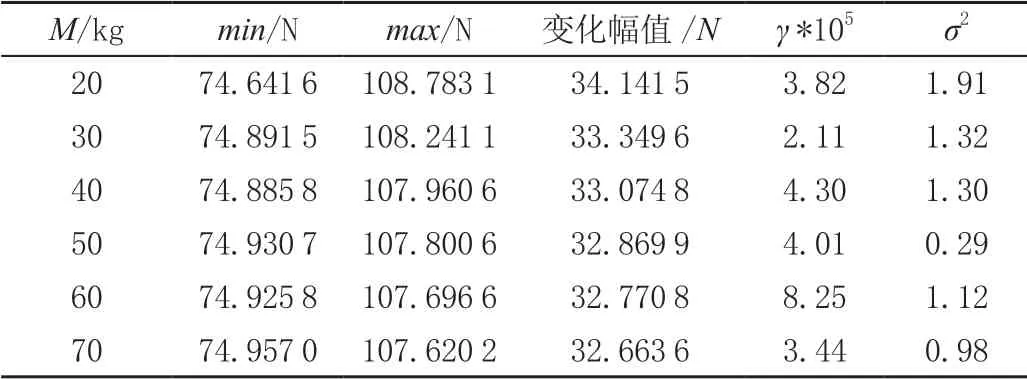
表1 不同受电弓等效质量下接触力变化情况

由表1 可知，弓头质量从20 kg 递增到70 kg，对应的接触力变化幅值从34.141 5 N 递减到32.663 6 N，接触力的变化幅值波动较小，表明一元受电弓等效质量模型的质量M 对接触力的变化影响较小。为了评估建立的LSSVM 框架下的弓网广义模型对于不同受电弓等效质量下的弓网接触力总体预测性能，我们计算了以上6 种质量下的弓网接触力的平均预测误差为0.037，说明建立的弓网广义模型对不同受电弓等效质量下接触力的总体预测精度也较高。所以，改变受电弓等效质量的大小对受电弓的受流质量影响不大。从表1 中5、6 列可知，不同等效质量的建模数据对应的弓网广义模型的超参数γσ、 的优化解也不相同。说明超参数γσ、 也会受到不同等效质量/不同批次的数据的影响，这与表1 的结果类似。此外，利用交叉验证法得到的6 种受电弓等效质量下的弓网广义模型的线性部分阶次n和非线性部分阶次m也相同，分别为n=2，m=1。

从以上数值仿真试验结果可以得出：接触力的大小与列车速度和弓网结构参数等息息相关，列车速度越大，受流越不稳定；一元受电弓等效质量对接触力的变化影响较小。该结果与文献[1]所述的规律基本一致，由于弓网模型参数设置各不相同，试验的具体结果会有差别，但不影响最终宏观的趋势性的结论，说明本文方法用于弓网接触力的建模和预报是有效的。本文方法对二元或多元模型的弓网系统建模研究提供了思路借鉴。

5 结语

从以上实验结果可以得出：弓网系统接触受流的好坏具体反映在接触力上，好的受流要求接触力的变化幅度较小，但须有一定的接触力使弓头与接触线靠近，从而保证稳定的接触受流。本文主要对一元受电弓进行等效试验分析，通过利用MATLAB 构建Simulink 模块搭建弓网系统动力学模型，通过对模型产生的理论数据进行预报试验，通过误差分析，验证基于改进的LSSVM 的方法的有效性。本文方法对二元或多元模型的弓网系统建模研究提供了一个理论基础。综上所述，随着现在列车速度的不断提高，必须对弓网系统进行动态特性的详细研究以及对弓网结构进行合理的设计，从而保证弓网稳定受流，列车安全运行。