基于虚拟力的WSN节点优化部署算法

李翠然， 谢健骊， 张昌西， 张华卫

(1. 兰州交通大学 电子信息工程学院， 甘肃 兰州 730070;2. 兰州交通大学 光电技术与智能控制教育部重点实验室， 甘肃 兰州 730070； 3. 徐州地铁运营有限公司， 江苏 徐州 221000)

无线传感器网络WSN (Wireless Sensor Network)以其监测精度高和覆盖区域广等特点，被广泛应用于战场数据收集、工业和环境监测等领域。由于WSN节点感知范围有限，为保证整个区域都在监测范围之内，需要确定适当的WSN覆盖策略。

在WSN覆盖策略研究中，采用虚拟力算法可使节点以较短的移动距离快速完成在覆盖区域的分散部署，有效降低了网络能耗。文献[1]给出了虚拟力的基本概念，即人造引力场中的“引力”和“斥力”，其合力导致引力场中的机器人产生相应的运动。在文献[2]提出的节点部署策略中，虚拟粒子用来表征节点，通过对虚拟场域中大量粒子的受力分析使粒子达到受力平衡的稳定状态。文献[3-4]提出了一种虚拟力算法VFA (Virtual Force Algorithm)，该算法中的节点以随机部署方式进行初始分布，根据对节点的受力分析可获知节点的下一步运动轨迹，从而完成节点在覆盖区域内的部署。然而，该算法可能存在的缺陷是：节点受力平衡是局部性事件而非全局性，这会使节点在监测区域内呈现出非均匀分布；相关权重因子在节点位置更新预测中的取值往往是预设的经验值，导致节点在受力平衡时依然存在较大的覆盖漏洞；节点的能耗主要由节点自身的移动及其在移动过程中与其他节点的碰撞导致，由此引起节点间能耗的不均衡。

为克服以上缺陷，本文提出一种优化的虚拟力节点部署算法WVFA，基于布尔感知模型和三角形网格划分，以最小化区域边缘处节点的冗余覆盖面积、实现覆盖区域内部的无缝覆盖为优化目标，通过对节点的受力分析推算出节点距离区域边缘处的欧氏距离，并将前一时刻节点所受虚拟力作为位置更新权重代入节点位置更新预测方程，从而缩小节点间的能耗差距、实现WSN的优化部署。

1 节点感知模型及其分布

1.1 节点感知模型

在VFA算法和本文算法中，WSN节点被看作是具有相互作用力的带电微粒。节点间产生相应的引力或斥力，是由节点间距离与某一给定阈值的大小比较决定的。算法的基本假设条件为：WSN节点的位置信息可通过GPS设备获知；节点配备全向传感器，感知数据可来自任意方向；节点具有一定的移动性；节点感知模型为布尔模型。

在2D监测区域内，令节点S和目标点t的位置坐标分别为(Sx,Sy)和(tx,ty)，节点感知半径为rs，则目标点t被节点S感知到的概率为[5-6]

( 1 )

式中：d(S,t)为节点S和目标点t之间的欧氏距离，可表示为

( 2 )

图1(a)和图1(b)分别给出了节点S的布尔感知模型和目标点t的感知概率分布。

1.2 节点的理想分布

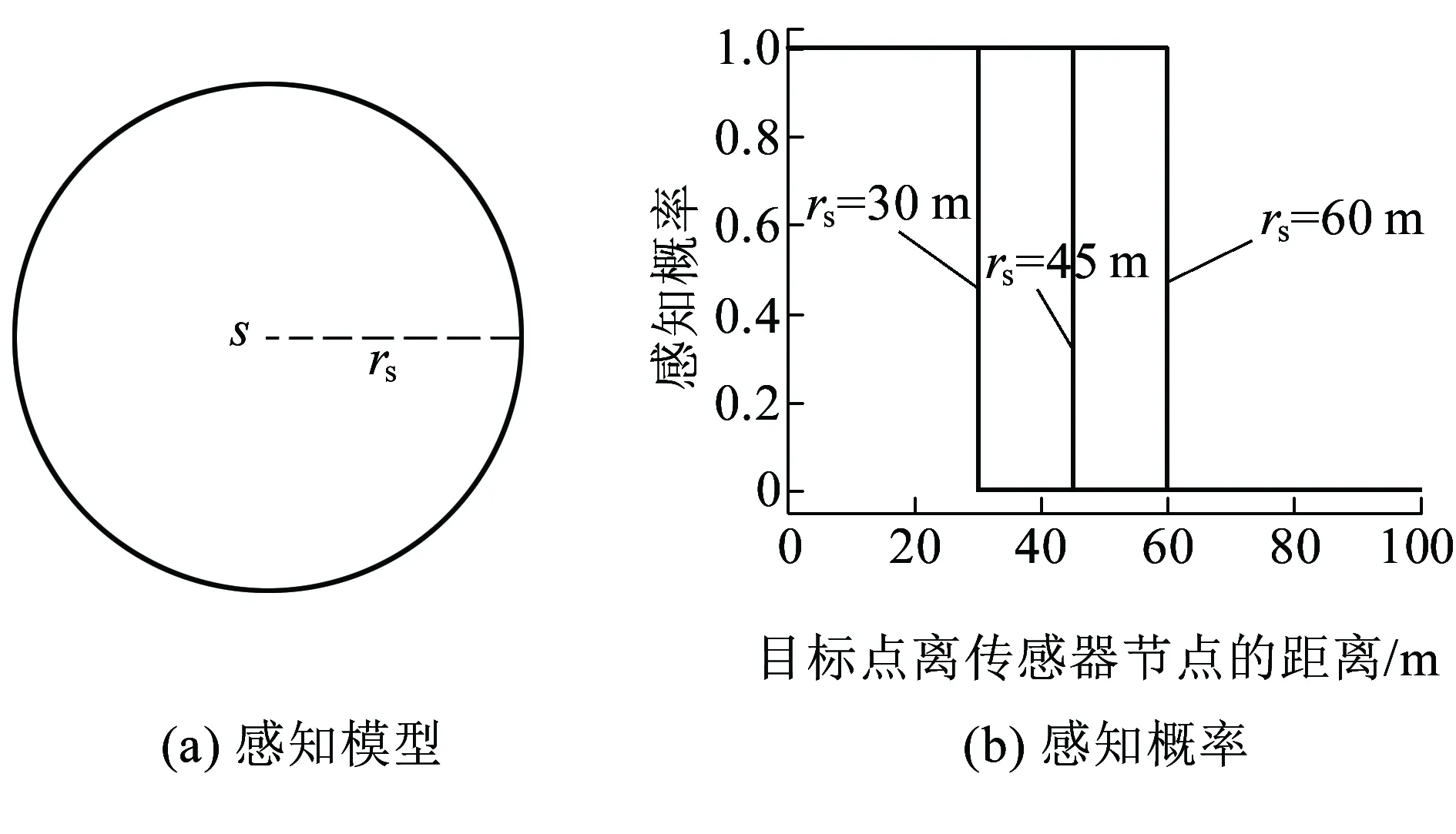
图1 布尔感知模型和不同rs下的感知概率

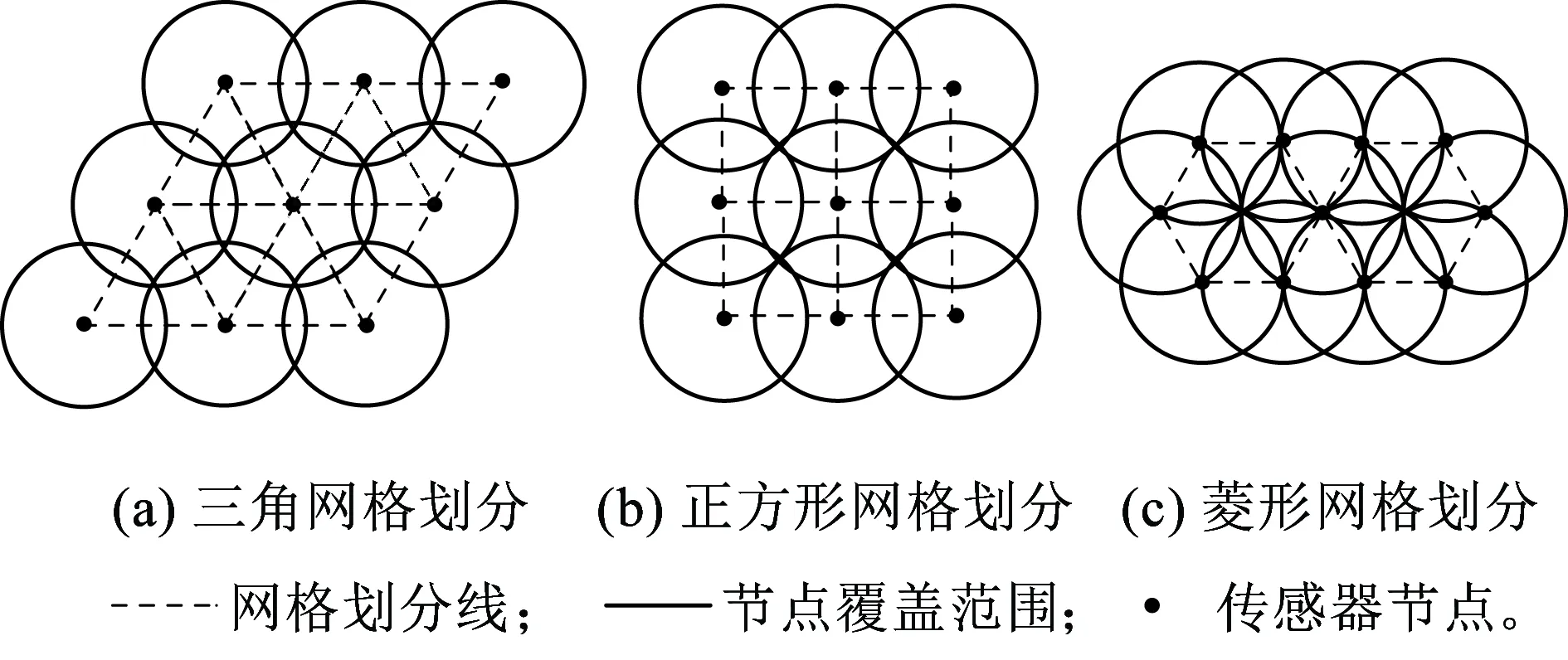
图2 3种网格划分方式

在监测区域边缘处，以无缝覆盖为目标的节点部署方式见图3。

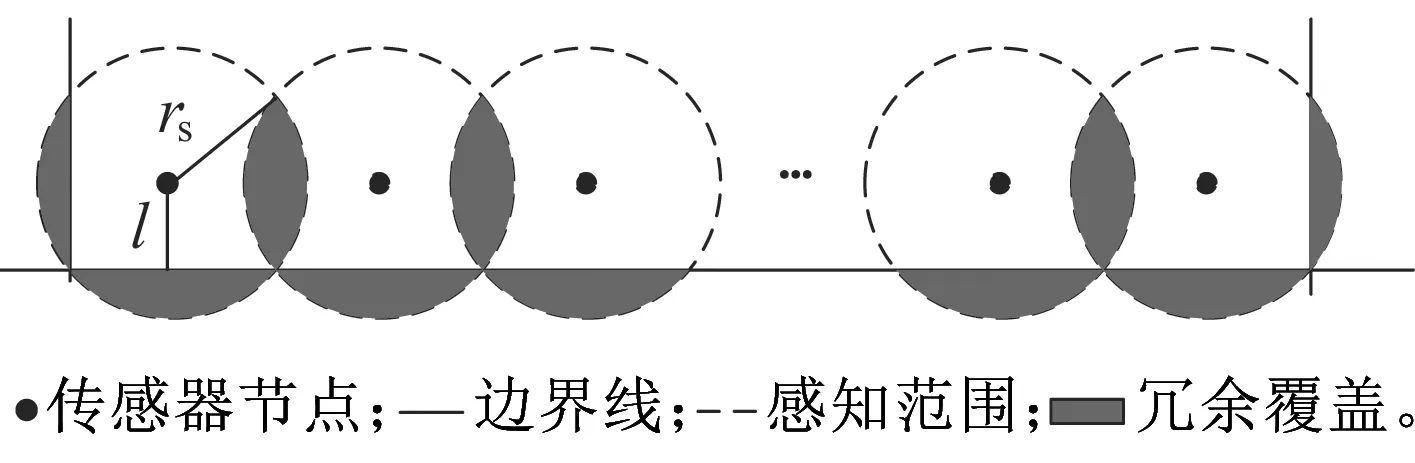
图3 边缘处的节点冗余覆盖示例

令N为监测区域边缘处的节点数目，则其冗余覆盖面积为

( 3 )

对S/N求导可使区域边缘处的冗余覆盖达到最小，于是可得

( 4 )

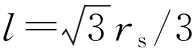
2 节点受力分析

2.1 节点间作用力

根据已有文献和前文分析，相邻节点间的距离为rs是保证监测区域无缝覆盖的充要条件。节点Si和Sj之间的作用力Ftij可表示为

( 5 )

( 6 )

以监测区域内的5个节点为例，节点间的相互作用力见图4(a)。图4中，节点S1，S2，S3，S4和S5所受的合力分别为Ft1=Ft1，2+Ft1，3+Ft1，4，Ft2=Ft2，1+Ft2，3，Ft3=Ft3，1+Ft3，2+Ft3，4，Ft4=Ft4，1+Ft4，3和Ft5=0。各节点在其合力作用下产生运动-受力分析，经多次运动后各节点达到稳定状态，其所处位置见图4(b)。图中，除节点S5的位置未发生变化外，节点S1、S2和S3以及节点S1，S3和S4分别构成正三角形。在实际监测区域内，节点分布一般较为密集，节点S5这种情况出现的概率极低，可不用考虑。

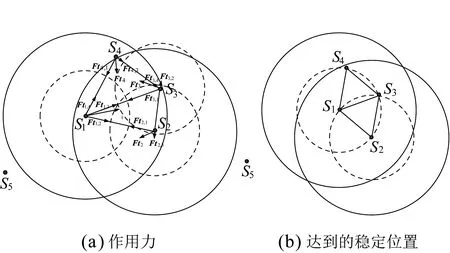
图4 节点间作用力和达到的稳定位置

2.2 区域边缘对节点的作用力

( 7 )

节点i所受合力为

( 8 )

图5(a)为节点S1受到的边缘离散点作用力。图5中，S1所受合力为Fn1=Fn1，3+Fn1，4+Fn1，5。节点S1在其合力作用下产生运动-受力分析，多次运动

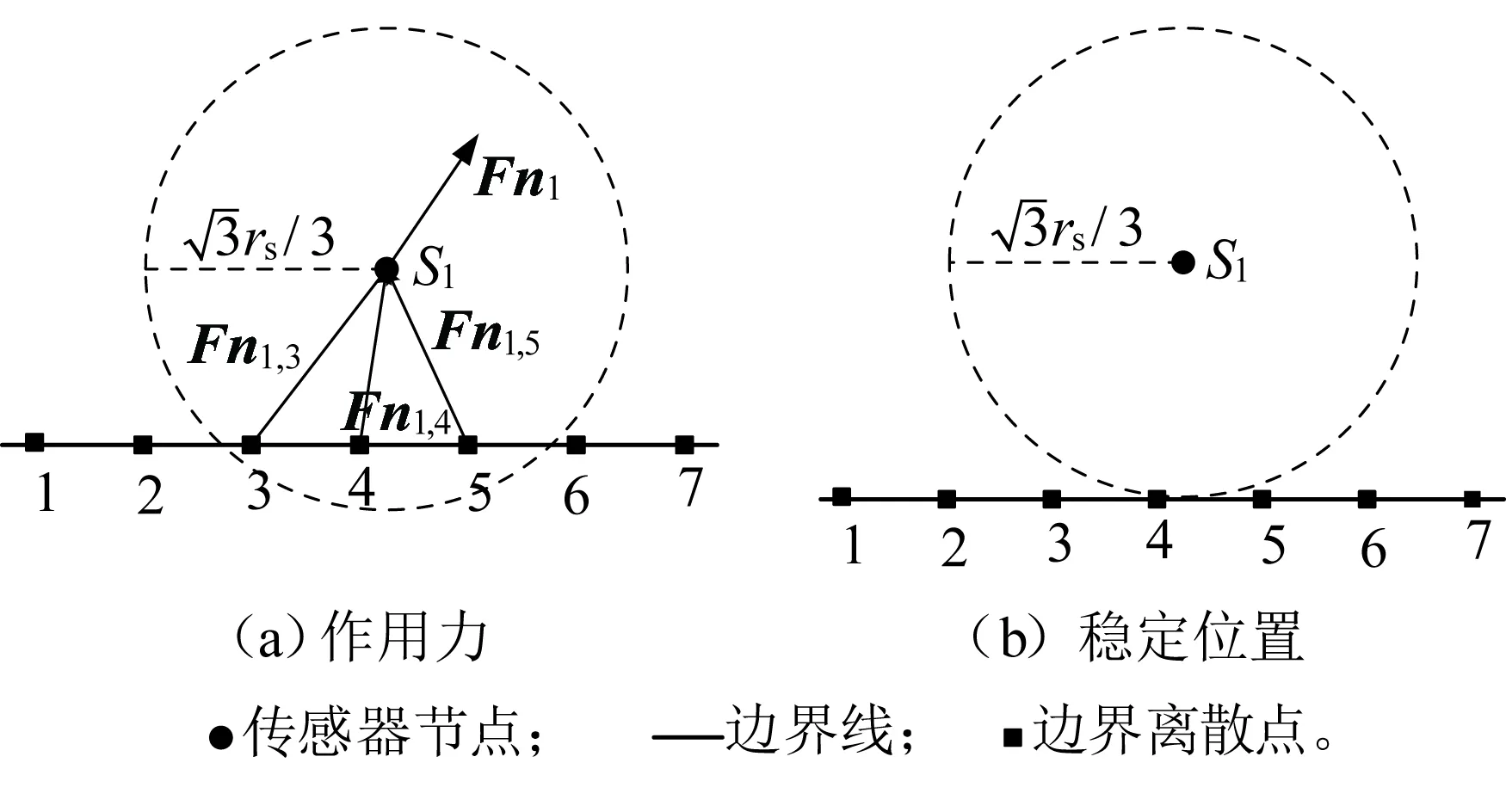
图5 离散点的作用力和节点移动后的稳定位置

后达到稳定状态的位置见图5(b)。可见，在WSN网络中，节点Si所受作用力由2部分构成：Fti和Fni，表示为

( 9 )

3 节点移动与位置更新

考虑到节点移动与其能耗之间的关联，为降低节点间的能耗差异，本文将节点前一时刻受到的虚拟力作为更新权重代入节点位置更新计算中，则节点Si在t步的移动距离di(t)和位置更新Si-new(t)分别为

(10)

(11)

式中：u为平衡权重(0≤u≤1)，它与达到覆盖要求的迭代次数相关；Fi(t)为节点Si在t步时所受合力；Si-ini(t)为节点Si初始位置；stepMax为节点Si最大移动步长。

由此，给出基于虚拟力的WSN节点优化算法WVFA的流程图见图6。

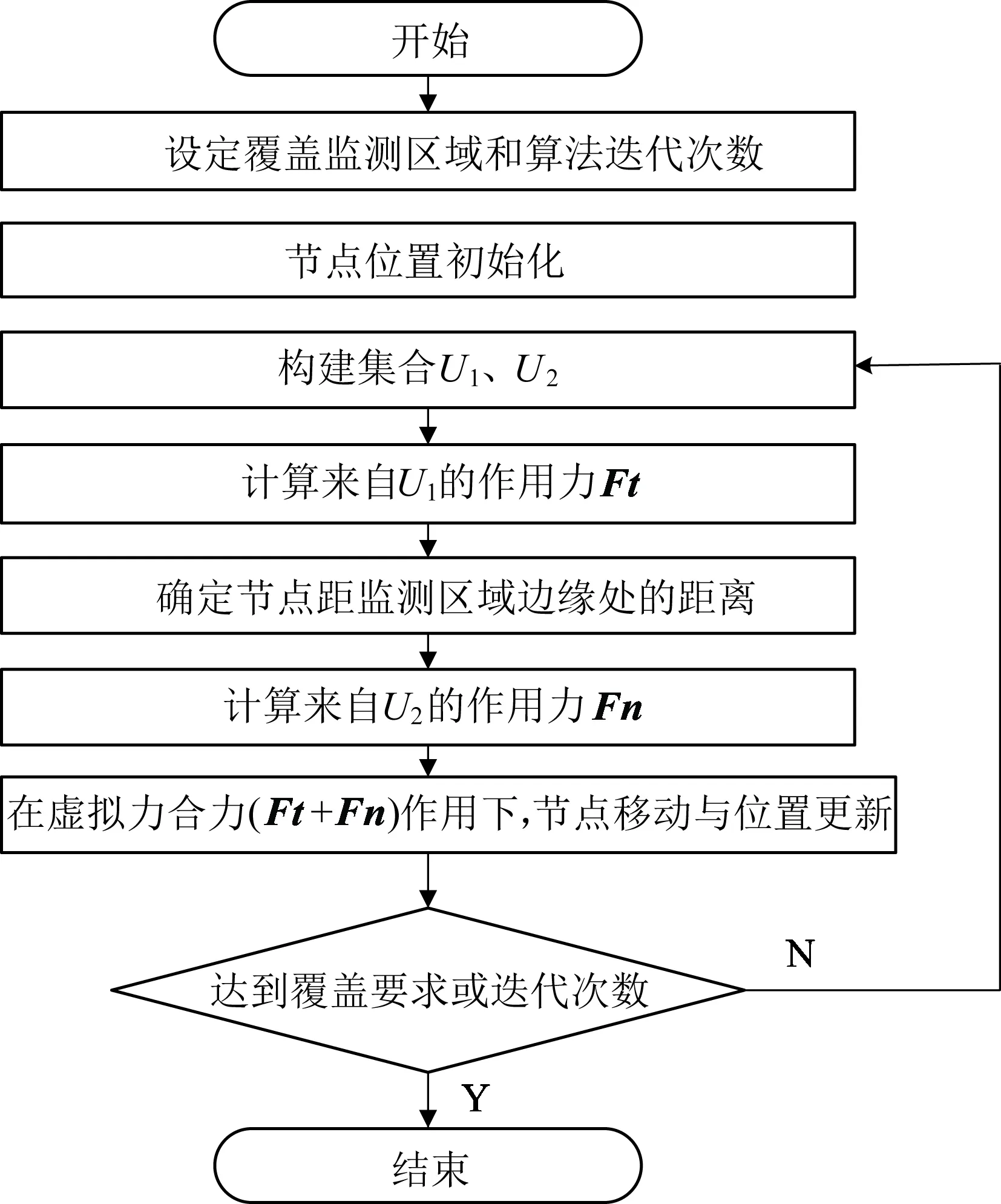
图6 WSN节点优化算法WVFA流程图

图7所示为WSN节点在监测区域内的初始分布。图8为不同迭代次数时的节点分布，由图8可看出，当迭代次数达到50时，节点位置基本维持不变，说明网络已处于稳定状态。图9(a)表示节点在监测区域内的运动轨迹，图9(b)表示网络覆盖率随迭代次数的变化趋势。

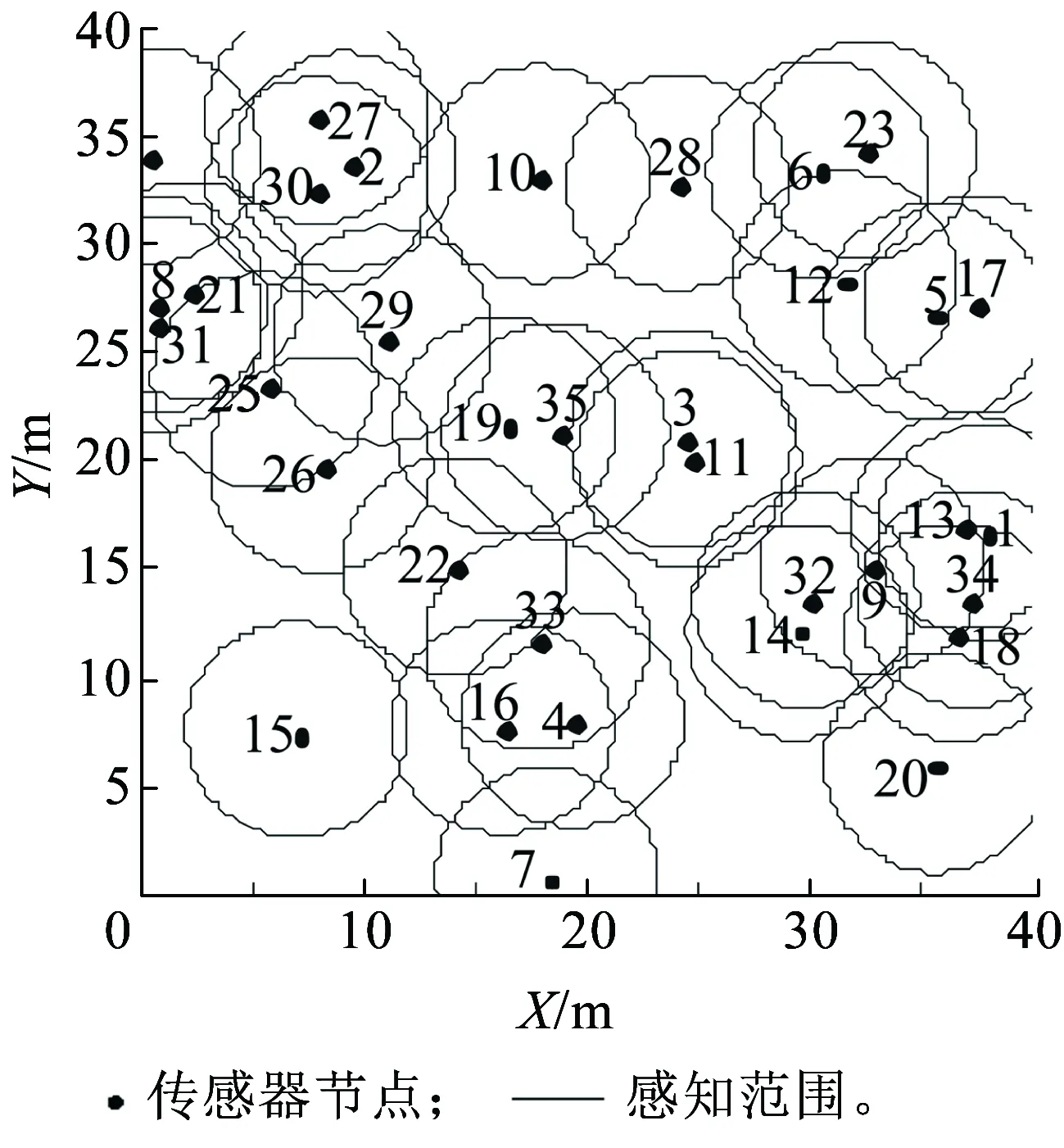
图7 监测区域内节点的初始分布

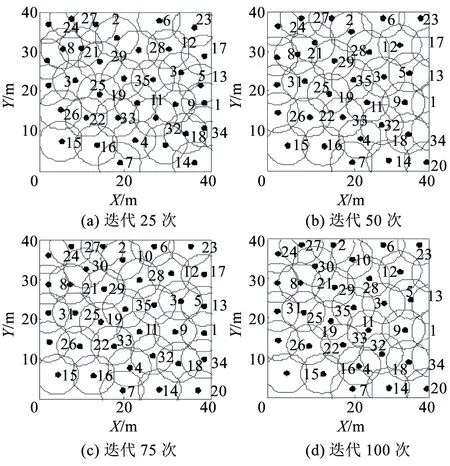
图8 不同迭代次数下的节点位置

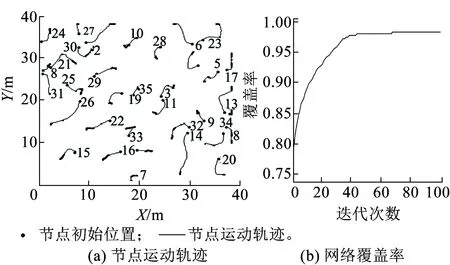
图9 节点运动轨迹和网络覆盖率性能

4 仿真结果

为仿真比较本文提出的WVFA算法与VFA算法[3]、CBS算法[11]、HLVFA算法[12]的网络覆盖率和节点能耗等性能，相关仿真参数见表1。

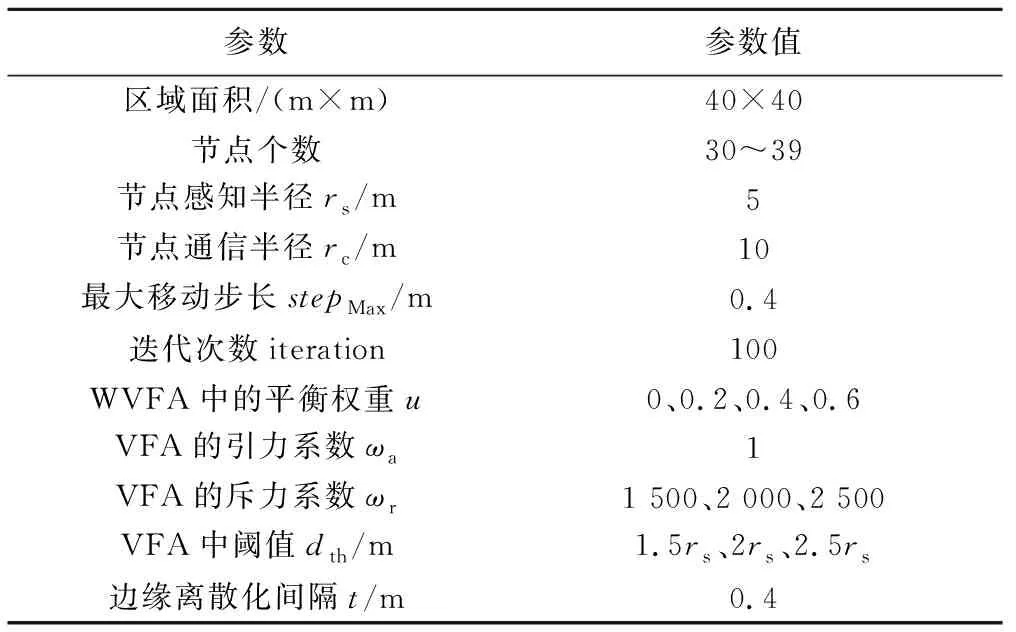
表1 主要仿真参数

图10为不同的权重u对网络覆盖率的影响。表2为不同u值时的节点平均移动距离davg、节点移动距离的标准差σ以及网络达到稳定状态时的覆盖率。可以看出，WVFA算法的收敛速度随着u值的增大逐渐变得缓慢，而不同的u值对稳定状态下的网络覆盖率影响甚微。此外，随着u值的增加，davg与σ的值减小。这说明，从降低节点能耗和缩小节点间能耗差异的优化目标出发，WVFA算法应选取较大的u值。

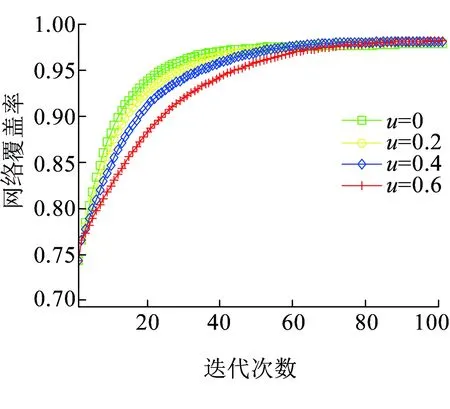
图10 WVFA算法中不同的权重u和网络覆盖率之间的关系

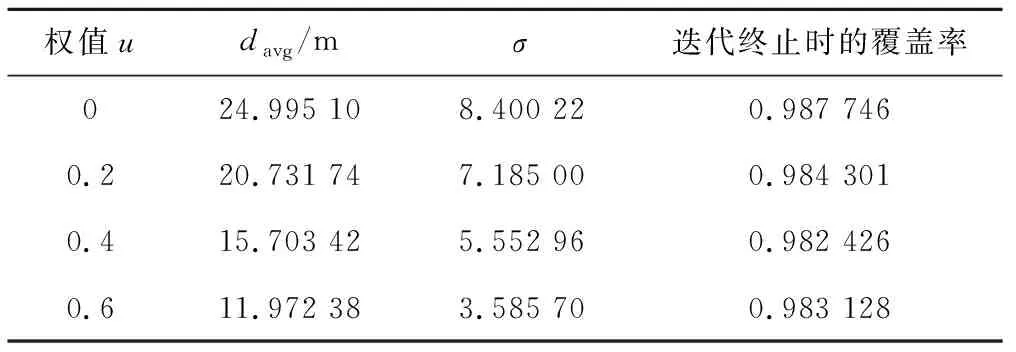
表2 不同权值u对应的WVFA算法中的参数值

为了对比算法性能，需要对VFA算法中的相关参数进行优化设置。图11(a)和图11(b)分别给出了参数dth、ωr与网络覆盖率之间的关系。由图11(a)可以看出，当dth=2rs时，网络覆盖率最大；由图11(b)可知，当ωr=2 500时，网络覆盖率最大。因此，VFA算法中的参数dth和ωr将分别取为2rs和2 500。

图12(a)、图12(b)分别为迭代次数和节点数目的变化对4种算法的网络覆盖率性能影响。由图12(a)可知，WVFA算法收敛速度较慢，这是由于该算法缩小了节点的受力范围，从而使节点的单次移动步长较小。此外，还可看出，WVFA算法在稳定状态时的网络覆盖率性能最优。由图12(b)可看出，4种算法的覆盖率均随着节点数目的增加呈增高趋势，WVFA算法的网络覆盖率最高。

图13(a)、图13(b)分别为节点数目与参数davg和σ之间的关系。可以看出，WVFA算法的davg值最小，同时该算法具有较小的σ值。综合来看， WVFA算法在降低节点能耗和缩小节点间能耗差异方面具有较优的性能。

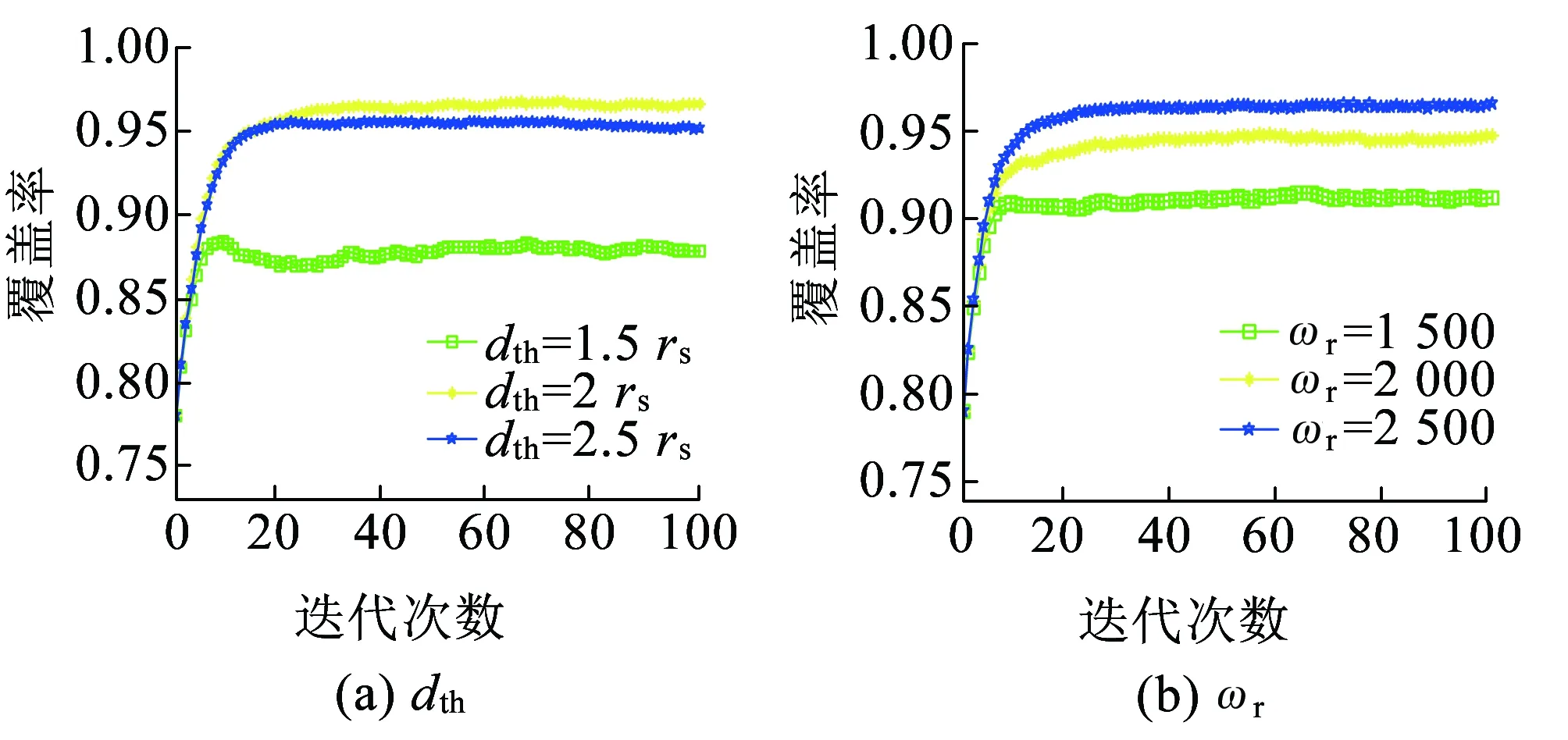
图11 VFA的阈值dth和斥力系数ωr对网络覆盖率的影响

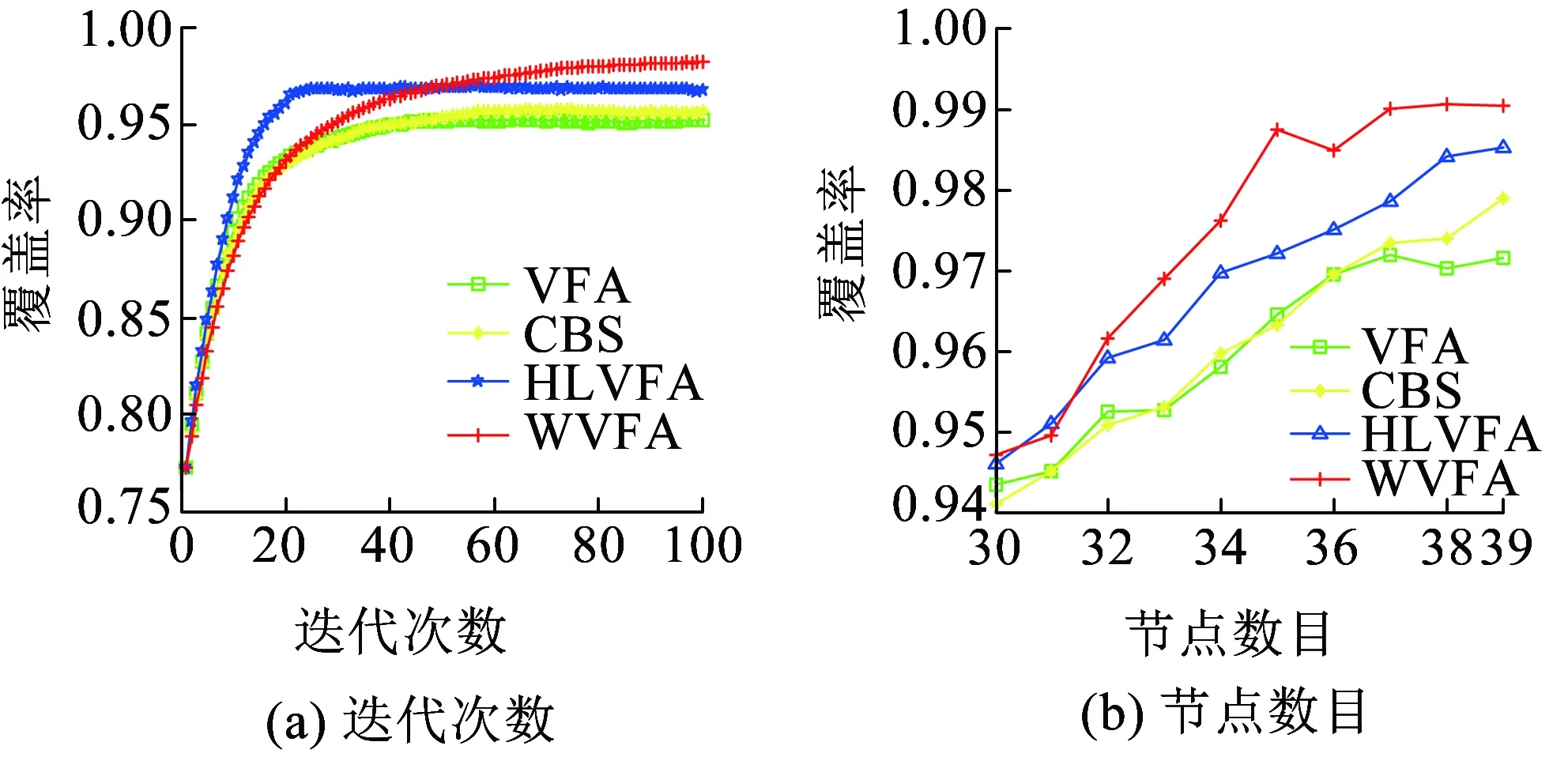
图12 迭代次数和节点数目对网络覆盖率的影响

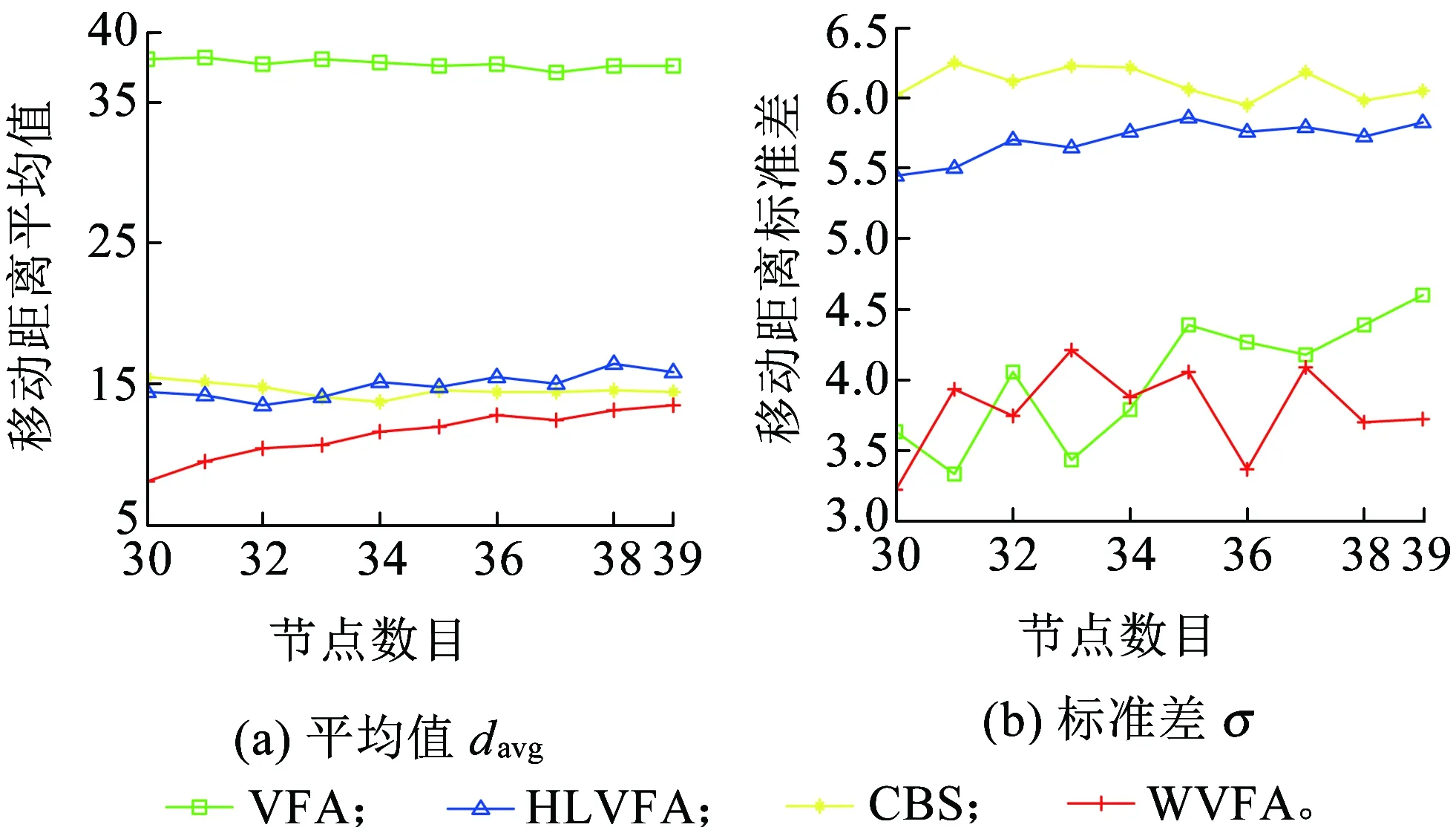
图13 不同节点数目下的节点移动距离的平均值和标准差

5 结束语

本文提出了一种基于虚拟力的WSN节点优化部署算法WVFA。仿真结果表明：WVFA算法在稳定状态时的网络覆盖率最高；WVFA算法的davg值为最小，同时该算法具有较小的σ值。因此，提出的优化部署算法能够在较低节点能耗条件下使网络覆盖率性能获得较大提高，实现了WSN的节能优化部署。