考虑声腔效应铁路箱梁低频噪声预测与降噪措施研究

宋 瑞， 刘林芽， 雷晓燕， 徐 斌， 罗文俊， 刘全民

(1. 华东交通大学 铁路环境振动与噪声教育部工程研究中心， 江西 南昌 330013；2. 南昌工程学院 土木与建筑工程学院， 江西 南昌 330099)

近十年我国轨道交通得到迅速发展，混凝土高架桥占线路总比例越来越高。箱梁具有抗弯、抗扭刚度大等受力优点，且采用预制吊装等施工工艺比较成熟，被广泛应用于高速铁路及城市轨道交通中。列车行驶于高架桥上导致结桥梁振动并辐射噪声，属于二次结构噪声，具有频率低，传播距离远的特点，长期在此环境下的人们容易引起各种心理生理疾病，桥梁结构低频振动噪声受到越来越多的重视。Bewes等[1]以一座钢-混凝土组合桥梁为研究对象，计算输入至桥梁的功率并采用统计能量法SEA(Statistical Energy Analysis)计算结构噪声。Ngai等[2]测试研究了香港西铁线路中一座混凝土高架桥的振动和噪声。高飞等[3]采用移动荷载模型计算了北京地铁5号线某高架的振动响应，并采用二维有限元声学模型分析了桥梁噪声的声场分布。Zhang[4], Li[5-6]基于车辆-轨道-桥梁耦合振动响应采用有限-边界元法FE-BEM(Finite Element-Boundary Element Method)对高速铁路混凝土箱梁噪声进行了较多的研究。李增光等[7]以及Wu等[8]结合频域的功率流方法和频域边界元技术对上海轨道交通高架线路上的U形梁和箱梁的噪声特性进行了对比。Li等[9]采用基于声模态传递向量和频域边界元来计算轨道交通桥梁噪声,他又联合功率流和无限元法IFEM(Infinite Element Method)计算了钢轨和桥梁的中低频噪[10]。宋晓东等[11]采用基于波数变换的2.5维边界元方法计算模态声传递向量，计算效率得到很大提高。Zhang等[12]针对一座噪声较大的公路钢桥，采用FE-BEM方法研究了桥梁周边声压分布，分析了车辆速度和路面不平顺对噪声的影响。

混凝土桥梁结构噪声属于低频噪声，采用有限元或边界元计算具有较高精度，但对于单元数量较大的模型，计算效率较低。统计能量法计算效率较高，但主要适用于研究中高频振动噪声。近年来，为了扩展统计能量方法的应用频率范围，很多学者致力于研究有限元-统计能量混合法(FE-SEA Hybrid Method)[13-14]。陈书明等[15]建立轿车FE-SEA混合模型，对FE模型施加激励荷载仿真计算车内噪声，采用实测方法验证了计算的准确性。罗文俊等[16]对振动频率范围较大的钢轨采用混合法模拟，2 000 Hz以上采用SEA模拟，平衡了计算精度与计算规模的关系。温华兵等[17]研究了双层加肋圆柱壳体在不同介质条件下对FE-SEA混合模型的声振影响。毛杰等[18]提取了轮轨噪声、二系悬挂力和空气动力噪声，将这三者耦合后作用于FE-SEA混合模型上，计算车内中频噪声。Zhang等[19]对钢轨、轨道板用SEA模型，箱梁采用FE模型预测了混凝土箱梁腔外噪声。

注意到，现有针对混凝土箱梁噪声大都采用FE-SEA计算，仿真模型为单跨两端开口结构，计算花费时间较长，桥梁噪声由各板件振动计算得到，忽略了声腔对腔外噪声的影响。实际上，箱梁开口位置上缘有伸缩缝遮蔽，下缘有混凝土墩顶提供遮蔽，且桥梁往往由多跨箱梁组成，箱梁构成了一个接近封闭声腔的结构，因此采用两端封闭结构计算更为准确；另外，现场实测试验表明声腔共鸣导致声腔内部噪声很大，实测最大声压能达到40 Pa(126 dB)[20]。声腔对结构空间噪声可能存在一定的影响。为了提高预测精度，考虑声腔的影响，在计算结构空间噪声时将声腔作为一个发声构件。基于以上原因，本文建立基于FE(结构板)和SEA(声腔)混合模型，分析桥梁结构各部件和声腔的模态密度、内损耗因子、声辐射效率等重要参数。采用FE-SEA方法计算桥梁结构腔外噪声并与不考虑声腔的模型进行比较，采用现场测试方法进行验证。分析讨论各结构板和声腔对各测点噪声贡献量，并探讨采用加设横隔板的方式降低桥梁结构噪声。

1 铁路箱梁结构噪声预测模型

1.1 车辆轨道耦合频域模型

(1) 车轮动柔度模型

本文主要研究的是20 Hz以上频段的结构振动噪声，二系悬挂通常在1 Hz左右。因此车辆模型中不考虑二系悬挂系统。1/8集总参数车辆模型从下至上依次为车轮、一系悬挂系统、 1/4转向架。车轮动柔度为

( 1 )

式中：mb、mw分别为转向架和车轮(及其上非悬挂部件)的质量；c1、k1分别为一系悬挂的阻尼和刚度系数。轮轨接触弹簧的柔度为αC=1/kH，kH为弹簧线性化接触刚度。

(2) 钢轨-轨道板-桥梁动柔度模型

钢轨采用无限长的Timoshenko梁模拟，其动柔度函数可表示为[21]

α(z1,z2)=B1exp(k1|z1-z2|)+

B2exp(k2|z1-z2|)

( 2 )

式中：B1、B2、k1、k2为与钢轨参数有关的系数。α(z1,z2)为在z2位置施加单位荷载引起z1位置处的位移。钢轨主要承受上部车轮荷载以及下部扣件荷载，其运动方程为

( 3 )

式中：N为扣件弹簧数；Pi为轮轨力；Kr为扣件弹簧刚度；Yri-Ysi为钢轨绝对变形量。

轨道板可采用两端自由Euler梁模拟，可采用模态叠加法计算，其动柔度可为

( 4 )

式中：NMS为振型数量；Wsn为Euler梁的第n阶振型函数，则轨道板的运动方程为

( 5 )

式中：Ks为CA砂浆弹簧刚度；Ysj-Ybj为轨道板绝对变形量。桥梁采用Euler梁模拟，其运动方程为

( 6 )

式中：Kz为桥梁橡胶支座的刚度；αb为桥梁的动柔度，可以采用模态叠加法求得。

联合式( 2 )、式( 5 )、式( 6 )并组合成矩阵形式为

K×Z=P

( 7 )

式中：K为由钢轨、轨道板、桥梁组合的刚度矩阵；Z为待求的结构位移矩阵，P为结构的荷载矩阵。通过式( 7 )即可得出钢轨、轨道板、桥梁各位置处的位移响应。其中钢轨的位移响应即为考虑了轨道板和桥梁刚度的钢轨动柔度。

(3) 频域轮轨力

考虑一系悬挂的1/8集总参数车辆模型，通过线性化的Hertz接触弹簧与轨道相互垂直作用。频域模型只能采用线性化轮轨接触刚度。不考虑车轮之间的相互影响，只计算单轮作用下的响应。轮轨力由车轮踏面和钢轨表面的不平顺的相对位移所激励产生，由于列车速度远小于行波传播速度，忽略车轮沿钢轨运动，代之以一个“移动的激励”拖动粗糙“带”通过轮轨间隙。轮轨动态力表示为[7]

( 8 )

式中：αW、αC、αT分别为车轮、接触弹簧、轨道(包含桥梁)的动柔度，即单位简谐载荷作用在各结构上引起的稳态位移响应；R为车轮和轨道的联合不平顺。

(4) 功率流模型

利用前面计算得到的车轮动柔度，钢轨动柔度以及轮轨接触动柔度得到总动柔度，代入式( 8 )即可以求出不平顺R激励下频域轮轨力Fc(ω)。将频域轮轨力代入式( 7 )中可以求出结构不平顺激励下的位移响应Z(ω)，则结构的速度响应表示为V(ω)=iωZ(ω)，钢轨-轨道板和轨道板-桥梁之间的内力为

( 9 )

根据功率流的定义公式，传递到钢轨和桥梁中的功率流分别为

(10)

式中：Re为进行实部运算；*为进行共轭运算。

1.2 混合FE-SEA法声辐射分析模型

混合FE-SEA法是基于波动耦合理论，将系统划分为FE、SEA两种子系统。将FE子系统中所包含的全部自由度表示为列向量q，而f表示作用在FE子系统各自由度处的外部激振力所组成的列向量时，FE子系统的运动方程可表示为[13]

(11)

FE子系统的总动刚度矩阵为

(12)

耦合边界上的混响力可表示为

(13)

系统输入到SEA子系统j的直接场的平均功率流可表示为

(14)

输出功率流Pout,j可表示为

(15)

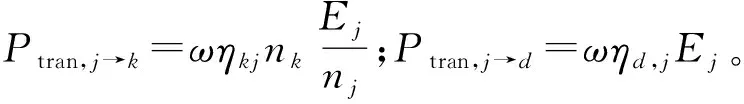
子系统自身消耗的平均功率流为

Pdiss,j=ωηjEj

(16)

子系统的能量平衡方程可以表达为

(17)

由于njηjk=nkηkj，式(17)可改写成

(18)

2 轮轨力计算及功率流分析

2.1 车辆轨道耦合模型参数

计算车辆模型参数参考文献[21]，桥梁为32 m双线混凝土简支箱梁，CRTS-Ⅱ型轨道板结构，钢轨采用CHN60钢轨。本文不考虑接触弹簧的非线性，接触弹簧的刚度取为1.31×109N/m2。模型计算参数见表1。

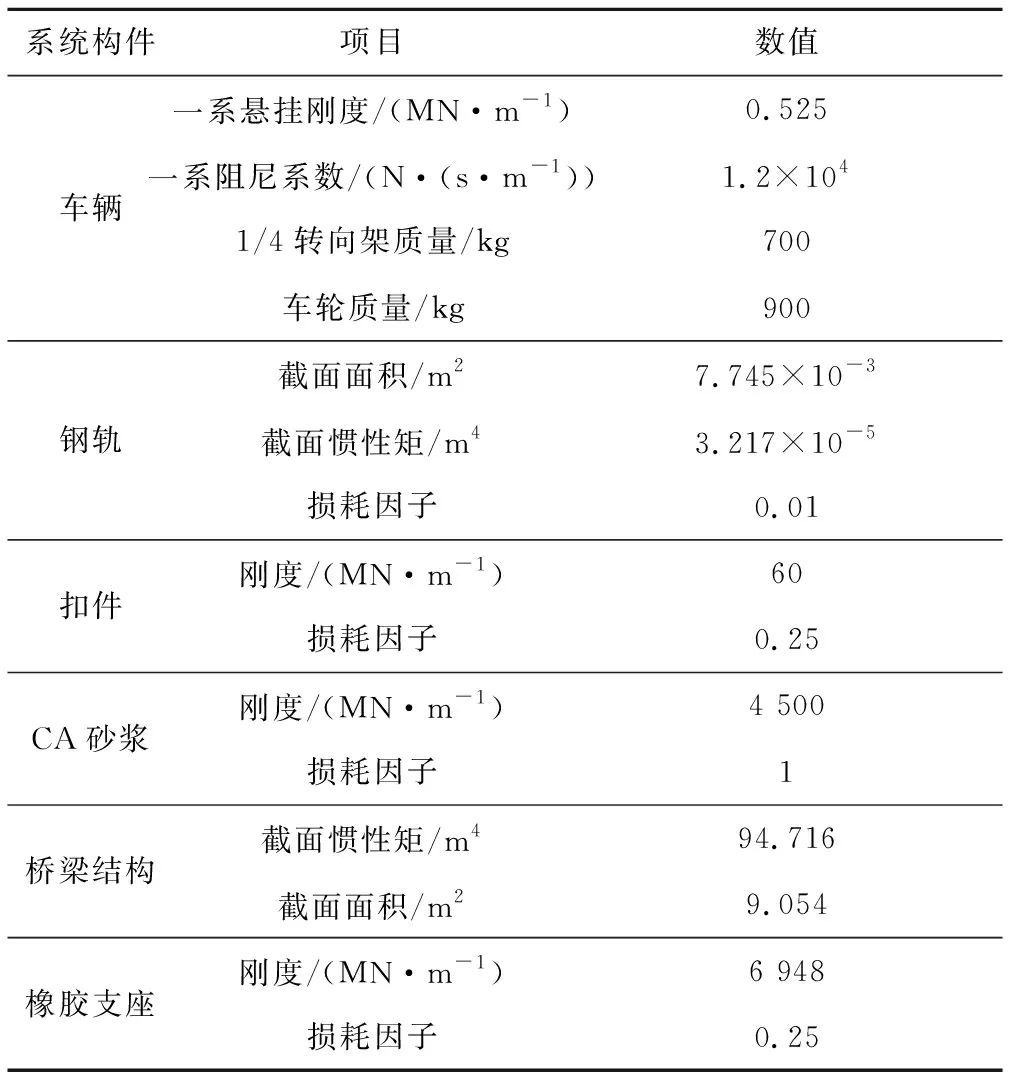
表1 模型计算参数

ISO 3095—2005提供了具有较好平顺性的轮轨不平顺谱，其不平顺幅值主要与波长有关，用式表示为

(19)

式中：r0为参考粗糙度，r0=10-6m；λ为粗糙度波长，与车辆速度和激励频率ω有关,λ=2πV/ω；r为不平顺幅值。

2.2 轮轨力计算

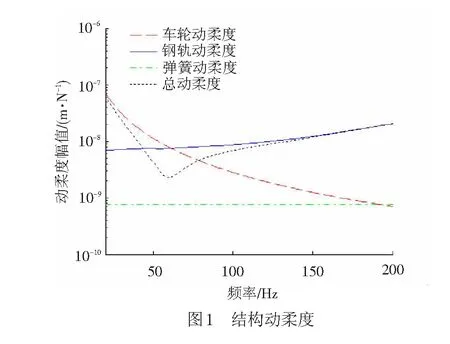
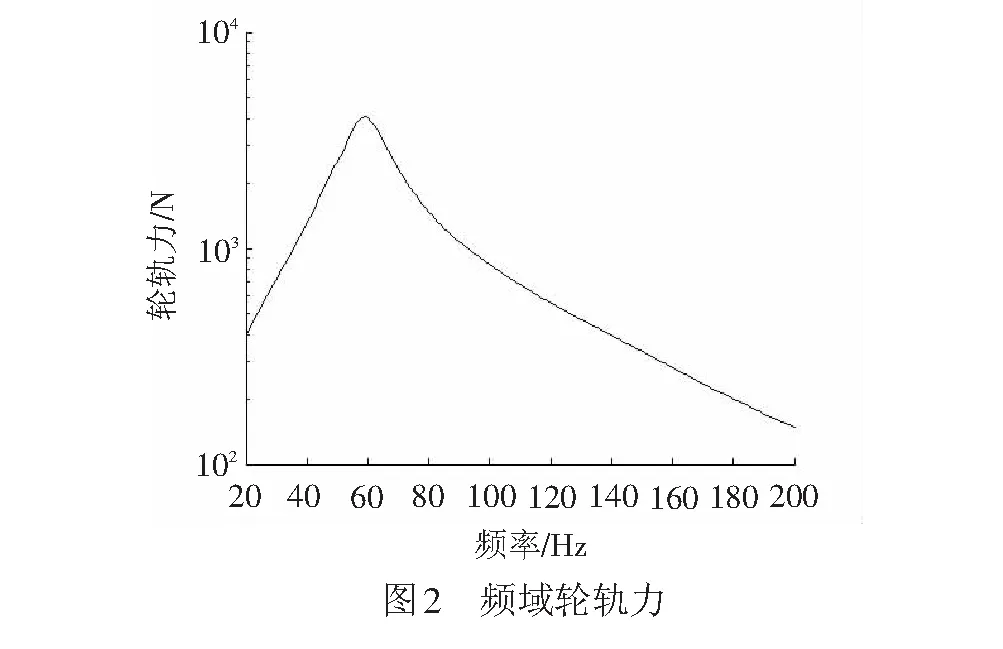
利用表1中计算参数，采用Matlab分别求出车轮、轨道和桥梁动柔度，见图1，接触弹簧的动柔度远小于钢轨的动柔度，车轮动柔度随着频率增大而减小，在20～40 Hz范围内车轮的动柔度起控制作用；钢轨动柔度随着频率增加而缓慢增大，在100～200 Hz范围内钢轨动柔度起主要作用。在60 Hz附近，车轮和钢轨动柔度幅值相等，相位相反，导致总动柔度出现极小值，该频率对应车轮-钢轨系统的固有频率。将总刚度和轨道不平顺代入式( 8 )中即可以得到频域轮轨力(见图2)，列车计算行驶速度按180 km/h计算。由图1可知，钢轨扣件刚度为60 MN/m时，系统总动柔度在60 Hz附近最小，轮轨力在60 Hz存在最大值，且其峰值与峰值对应的频率随着钢轨扣件的增大而减小。

2.3 输入至桥梁功率流

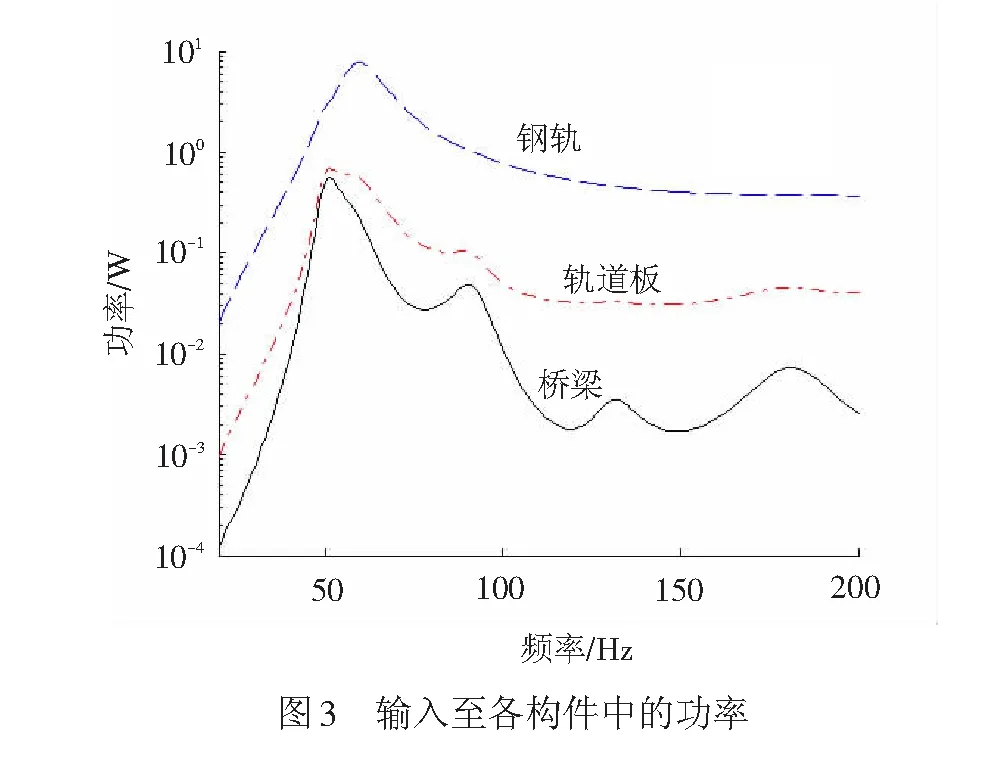
输入功率反映了输入至结构中的能量大小，通过计算输入到各子结构中的功率，可以计算求得子系统的平均速度。图3为输入至钢轨、轨道板、桥梁中的频率-功率曲线，从图中可以看出，三条曲线整体上呈现先增大后减小的趋势，钢轨在60 Hz附近输入功率最大，其原因主要是在这一频率段轮轨力最大。而轨道板和桥梁的最大输入功率对应的频率为50 Hz。随着频率增大，在100 Hz以后，输入至钢轨中的功率变化比较平稳，而输入至轨道板和桥梁中的功率随着频率的增大而迅速的减小， 且输入至桥梁的功率较输入至轨道板中的功率衰减更快，这是由于CA砂浆阻尼远大于钢轨阻尼，随着频率的增大，更多的能量被CA砂浆的阻尼所消耗，导致传递到桥梁中的功率迅速降低。

3 噪声数值计算与现场测试

3.1 FE-SEA模型参数

(1) 模态密度

模态密度是指各子系统或结构部件在某一频段范围内的模态数，反映了结构或子系统对于外部激励引起共振响应的能力。模态密度越大，结构从宽带激励吸收能量的能力越强。针对混凝土箱梁结构，由顶板、翼缘、腹板和底板等若干板结构基于强耦合组成，除翼缘板厚有一定厚度变化外，其他板件厚度均可视为定值，板的模态密度可通过解析方法得到

(20)

式中：t为板的厚度；A为板的面积。而对于一个长方体壁面的三维空间声场，其模态密度为

(21)

式中：V0为声腔的体积；Ca为声波波速。图4为各结构板和声腔的模态数，从图中可以看出，各板的模态数随着频率的增大而缓慢增大，而声腔的模态数急剧增大。在200 Hz中心频段，顶板、腹板、声腔分别含有17、5、430个模态数，200 Hz范围内结构板的模态主要落在中低频段，而声腔在40 Hz频段内后，进入了高频区。因此，从模态密度角度分析，结构板采用有限元法建模，声腔采用统计能量法建模是比较合适的。

(2) 内损耗因子

内损耗因子是指子系统在单位频率内单位时间损耗能量与平均存储能量之比，一个结构子系统i的内损耗因子ηi由三种彼此独立的阻尼组成。箱梁结构的损耗因子采用如下公式计算

ηi=ηis+ηir+ηib

(22)

式中：ηis为子系统本身材料内摩擦构成的结构损耗因子；ηir为振动声辐射阻尼形成的损耗因子；ηib为边界连接阻尼构成的损耗因子。板件之间可认为是刚性连接，可以忽略ηib，因此箱梁结构的耦合损耗因子由材料物理属性决定的结构损耗因子和声辐射阻尼耦合损耗因子。本文中混凝土的结构损耗因子ηis=0.015，对于声辐射阻尼耦合损耗因子可简化为结构对声场的耦合损耗因子。

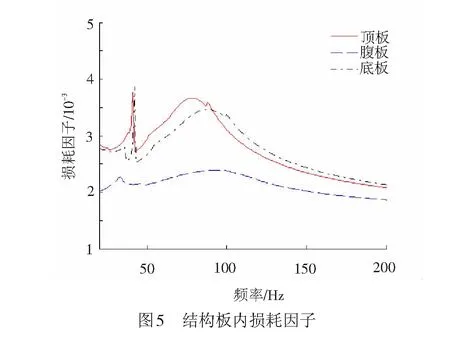
图5为部分板件的内损耗因子示意图，从图中可以看出，顶板和底板分别为0.3 m和0.28 m，厚度接近，其损耗因子曲线比较接近，而腹板厚度为0.45 m，较底板和顶板厚，板宽较顶板和底板小，且其声辐射耦合因子较其他板更小，导致内损耗因子较其他板更低。注意到在40 Hz附近，底板和顶板的内损耗因子存在一个峰值，表明在这个频率范围内声固耦合效应比较明显，而腹板的耦合效应不明显。对于混凝土声腔，其内损耗因子可采用理论公式计算[22]，即

(23)

式中：T60为混响时间，指声场达到稳定状态，声源停止发声后，声压级衰减60 dB所用的时间；平均吸声系数αT和混响时间T60存在下面的经验关系式

(24)

式中：V为声腔的体积；C0为空气传播速度；S为声腔的表面积。从式(24)可知，声腔的内损耗因子随着频率增大，其内损耗因子急剧减小，腔内能量不容易消散。

(3) 声辐射效率

由振动板辐射的声功率由下式确定

Wrad=ρ0c0σS

(25)

式中：ρ0为空气密度；c0为声速；S为板表面积；为结构表面振动的均方速度；σ为辐射率。

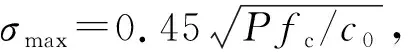
3.2 振动噪声测点布置

试验选取对象为某高速铁路32 m双线混凝土简支箱梁。CRTS-Ⅱ型轨道板，CHN60钢轨。测试位置位于桥梁正下方的一条公路上。一侧为既有线路，另一侧较为开阔，选择较开阔一侧开展测试研究。为了保证测试的准确性，在测试过程中采取短暂封闭交通形式，同时避开既有线路列车运行，测试现场图如图7所示。图8为桥梁跨中截面噪声测点布置图，测试采用德国HEAD公司生产的HEAD Recorder测试系统，声传感器采用GRAS393B04，用支架架设于指定位置。振动加速度传感器采用PCB40PH，在测试位置将混凝土打磨平整并粘贴小钢板，将加速度传感器紧密粘贴于小钢板上。采样频率为10.24 kHz，采用手动触发方式，当列车接近测试桥跨时开始采集。当列车通过测试桥跨时，采用测速仪测量列车通过速度。振动加速度数值采用列车速度为183.3 km/h。通过现场测试10次上行列车，其通过该桥梁的速度主要在165～192 km/h之间，取速度的平均值为180 km/h，相应的实测噪声也取其平均值分析。

3.3 振动测试分析

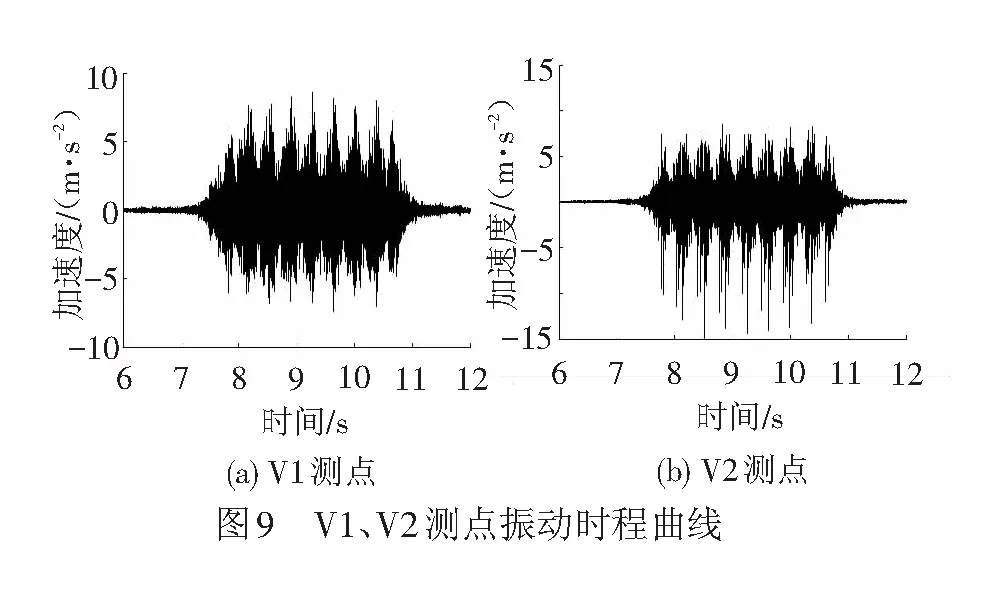
图9为跨中部位顶板、底板中部两个振动加速度V1、V2测点的实测法向振动时程曲线。由于箱梁顶板直接承受车轮的竖向向下荷载，顶板的最大竖向负加速度为15.07 m/s2,最大正加速度为8.45 m/s2。从时程曲线可以看出，每个峰值对应车轮作用于测点位置，从列车第一个车轮驶入跨中截面到最后一个车轮驶出跨中截面，一共持续3.24 s，列车从第一车轮至最后车轮全长164 m，计算列车速度为182.2 km/h，这与采用测试仪测试的速度基本吻合。时程曲线中每个峰值对应车轮，第一转向架和后转向架位置附近2个峰值，其他7个位置有4个峰值，对应前车后转向架和后车前转向架，峰值比较密集，而车辆前转向架和后转向架间间距较大，为15.5 m，从时程曲线中可以看出峰值间具有较长时间间隔。图9(b)为底板中部测点V2振动加速度时程曲线，由于底板承受垂直向上支座荷载，其正加速度幅值大于负加速度幅值，其最大值分别为8.06、7.37 m/s2。

3.4 FE-SEA模型建立

建立单跨混凝土箱梁模型，其中混凝土板由FE模拟，声腔采用SEA模拟。对于铁路混凝土箱梁，两端为开口结构，文献[20]认为箱梁开口位置上缘有伸缩缝遮蔽，下缘有混凝土墩顶提供遮蔽，对开口与封闭两种模型进行分析并和实测结果比较，分析结果表明，腔内噪声采用封闭结构仿真结果与实测结果更为接近，故本文采用封闭结构形式进行分析。为了形成一个封闭声腔，在箱梁两端加设横隔板，同时尽量减小设置横隔板对结构振动的影响，横隔板厚度取为0.1 m。混凝土结构内损耗因子取0.015，声腔内损耗因子采用式(23)的计算值。同时建立开口结构不考虑声腔的箱梁模型进行比较。

3.5 测点声压对比

图10为N1、N2、N3三个测点的声压实测值和理论值对比图。从图10中可知：

(1) 考虑声腔较不考虑声腔的理论值更接近实测值，考虑声腔的理论值精确度更高，采用FE-SEA方法计算的封闭箱梁结构噪声具有较高的准确性。

(2) 桥梁的声压级峰值频率主要集中在50～80 Hz范围内，其主要原因是在这一频率范围内轮轨力最大导致。对于N2和N3测点，20～31.5 Hz和125～200 Hz范围内实测值偏离理论计算值较大，其原因可能是其他噪声比如气动噪声、车辆噪声、轮轨噪声等非桥梁结构噪声对实测数据有较大的影响，而对于N1点，由于紧贴箱梁梁底，箱梁的遮蔽效应隔离了大部分的非桥梁结构噪声，实测值与理论值吻合度较N2和N3点高。

(3) N1、N2、N3测点最大实测声压级分别为93.4、89.3、80.3 dB，距离箱梁距离越远，其最大声压级越逐渐降低。

3.6 声贡献度分析

为了分析各结构部件及声腔的辐射能力，分别计算翼板、顶板、腹板、底板和声腔对测点总声压的影响，表2为各构件对三个测点的声压级，图11为各板件及声腔的贡献率示意图，通过比较各板件的声压和总声压级可知：

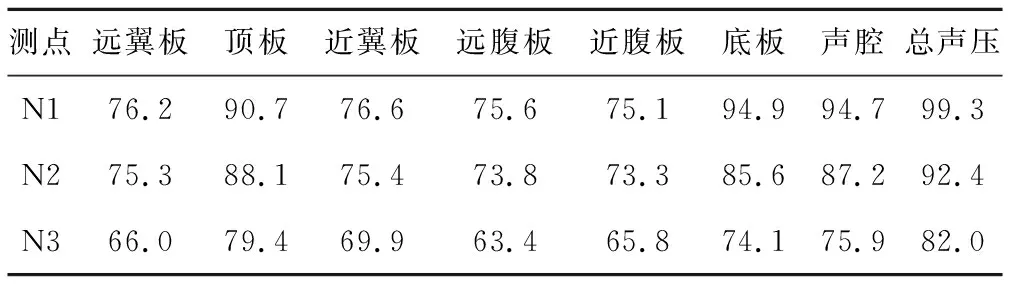
表2 各构件声压级 dB

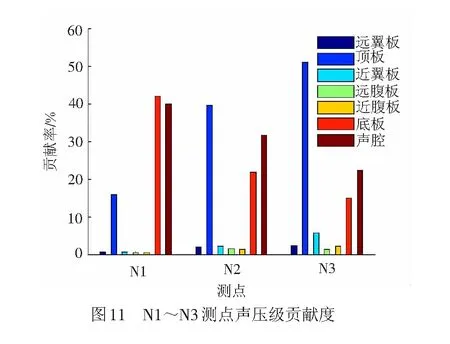
(1) 对于跨中截面梁底正下方0.3 m位置处的测点N1，底板、声腔、顶板的贡献率分别占42.1%、40%、15.8%，其他板贡献量均小于1%，可忽略不计。由于测点靠近底板位置，底板贡献量最大，而由于列车高速运行，导致腔内产生声腔共鸣，透过底板往外辐射噪声，导致由声腔产生的声压的贡献率达到42.1%。

(2) 对于N2测点，其声压贡献量从大到小依次为顶板、声腔、底板、翼板、腹板，其声压贡献率分别为39.5%、31.6%、21.9%、4.2%、2.8%。由于N2测点远离底板，底板声压贡献率降低，顶板和声腔的贡献率最大，而由于遮蔽效应降低，翼板的振动对N2测点的噪声有一定的贡献。

(3) N3点为距离桥梁中心20 m远,距离地面1.5 m高测点，从图11中可以看出，顶板的振动引起的噪声占总声压的51.0%，顶板振动是远场噪声的主要来源。底板和声腔的贡献率分别为15.1%、22.4%，声腔依然在总声压贡献中占有重要的作用，因此对于20 m远的噪声测点，声腔的作用依然不能忽略。

(4) 从图11可以看出，对于N1、N2、N3测点，分别计算了各结构板和声腔对测点的声压，其中声腔的声压级贡献率分别为42.1%、31.6%、22.4%，采用声压级贡献度的形式很好的体现了声腔对腔外噪声测点的影响。

4 降低噪声措施

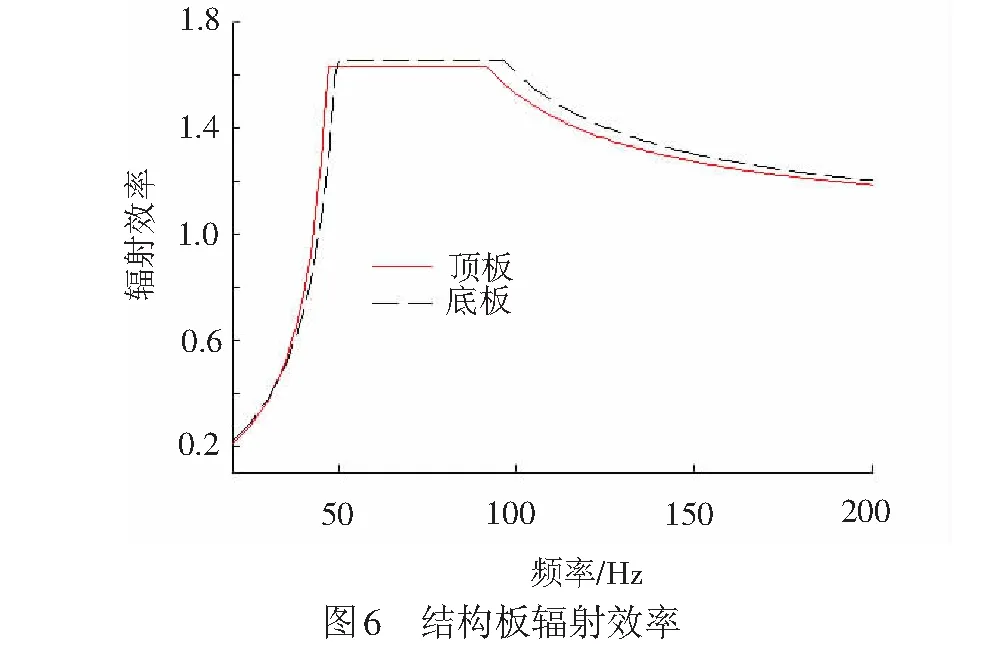
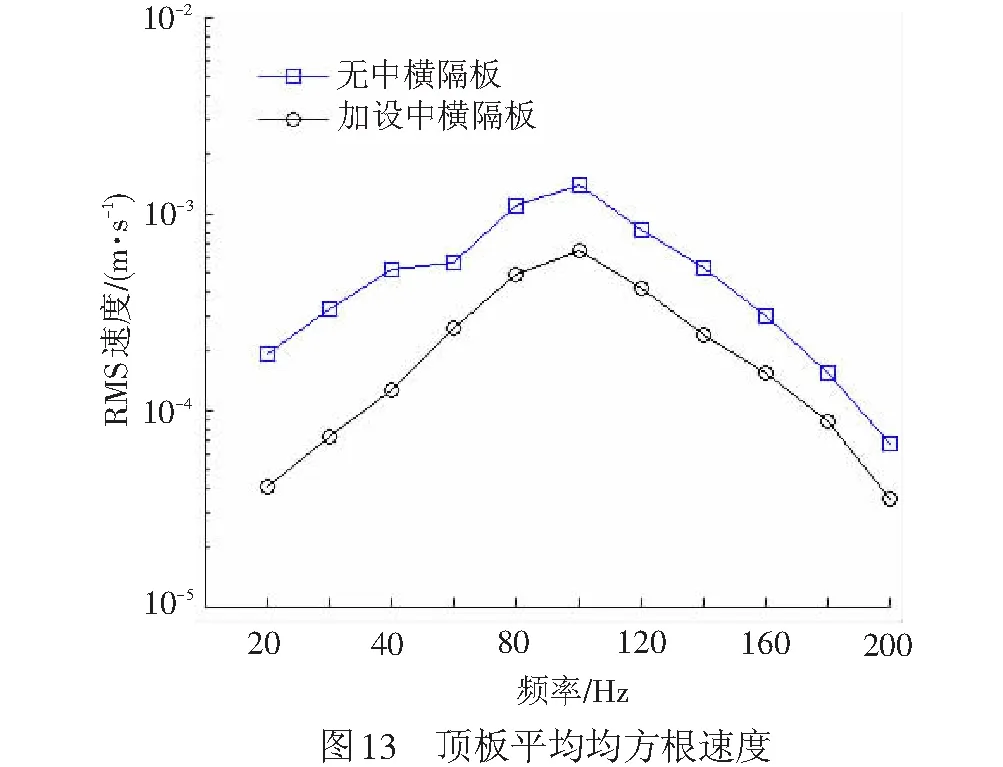
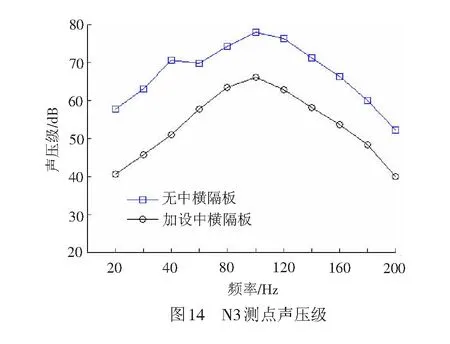
从声压贡献度分析可知，随着离桥梁距离的增大，顶板的贡献量所占的比例越大(见图11中蓝色部分)，如N3测点其顶板的贡献度超过50%。顶板直接承受上部列车荷载，且其辐射面积较大，图6可知其辐射效率较高，顶板是引起桥梁远场噪声的主要构件，因此对于一定距离远的噪声测点，降低顶板引起的振动噪声是控制桥梁噪声的关键。有文献表明，在U梁上加肋，能够有效的降低空间结构噪声[24]，因此在箱梁内部均匀的设置三个横隔板，两端各设置一个端横隔板，横隔板与顶板、底板、腹板刚性连接，横隔板厚度0.3 m。图12～图14分别为有无中横隔板情况下腔内声压、顶板振动速度和N3测点声压的理论值对比图，从图中可以看出：

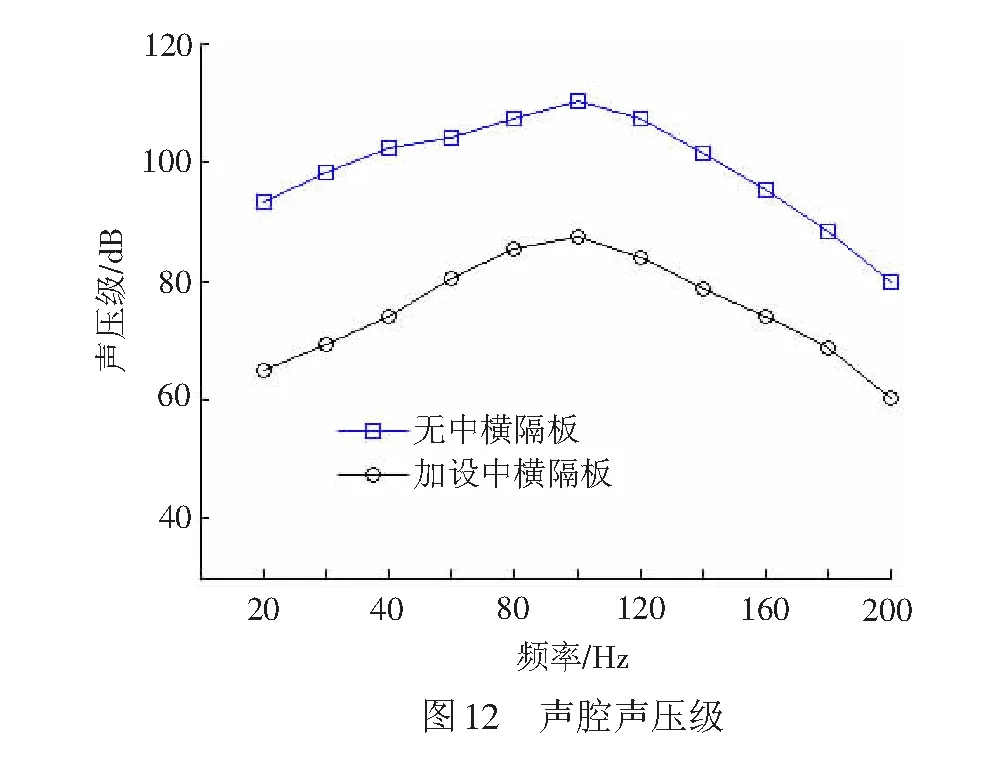
(1) 同等情况下加设中横隔板后，腔内声压最大峰值声压级由110.2 dB降至87.3 dB，声压级降低达22.9 dB，其原因主要是由于加设中横隔板后，箱梁声腔由一个声腔分割成四个声腔，声腔模态密度大大降低，以100 Hz中心频率为例，未加横隔板时，声腔模态密度为94.2，而加上横隔板后，其模态密度降为17.2，模态密度越小，声腔越难从宽带激励中吸收能量，故其声压级越低。

(2) 在中心频率63 Hz位置，顶板空间平均均方根速度由1.41×10-3m/s降为0.68×10-3m/s，降幅达53.9%，表明加设横隔板后能有效的抑制顶板振动，由式(25)可知，结构的声功率与板的结构表面振动的平均均方根速度线性相关，平均均方根速度越低，声功率越小，相应的声压级也越小，因此降低桥梁顶板的振动速度能有效降低桥梁结构噪声。

(3) 由于声腔声压级降低，且顶板振动速度降低，通过图11可知，N3测点中声腔和顶板的贡献量达到总声压级的75%，声腔声压级和顶板振动速度的降低导致远侧测点的声压级降低，在63 Hz峰值频率位置，其声压级由78.0 dB降为66.2 dB，降低了11.8 dB，表明采用横隔板能有效的降低桥梁结构噪声，采用横隔板降低桥梁结构噪声有效可行的。

从上文可知，加设横隔板能有效的降低桥梁顶板的振动，但会增加原材料的用量，且对桥梁预制模板等施工工艺提出了更高的要求，一定程度上会增大施工成本，因此有必要对加设横隔板的数量和间距作进一步的研究。建立五种不同的横隔板布置工况形式，其中横隔板的厚度均为0.3 m，横隔板与顶部、腹板和底板刚性连接，分别计算N3测点的噪声，计算结果见表3。从表中可以看出，随着桥梁横隔板数量的增加， N3测点位置处的声压级逐渐降低。当箱梁无中横隔板时，其总声压级为82.0 dB，当设置2个中横隔板时，其声压级缓慢降低至76.4 dB，声压级降低了5.6 dB；当设置3个中横隔板后，其声压级较设置2个中横隔板声压级降低了6.3 dB；当设置4个中横隔板较设置3个中横隔板仅降低了1.7 dB，降噪效果有限。综上所述，从节约成本和有效的降低桥梁结构噪声的角度出发，32 m箱梁采用两个端横隔板和三个中横隔板的构造布置是比较合适的，相关的研究可以为桥梁减振降噪设计提供一定参考。

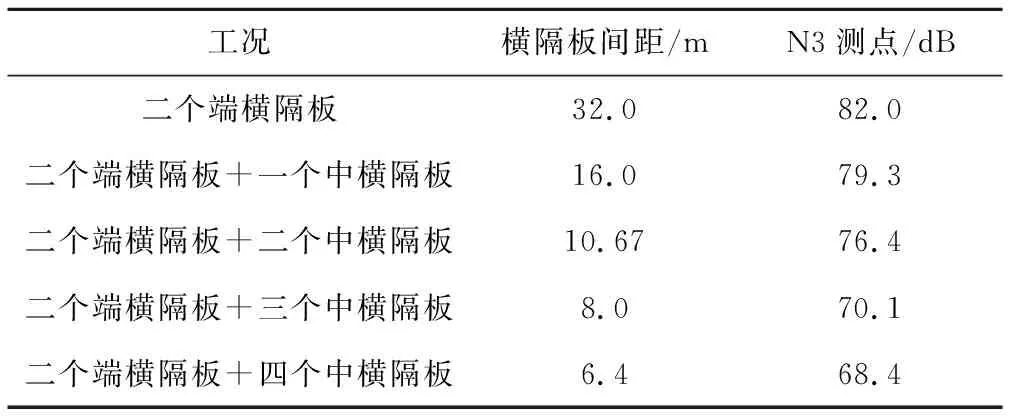
表3 不同工况N3测点总声压级

5 结论

采用动柔度法计算轨道、车轮和接触弹簧刚度，进而计算出频域轮轨力和输入至桥梁的功率。采用混合FE-SEA方法计算了箱梁结构不同空间位置的噪声并采用实测数据验证了方法的准确性，分析了箱梁不同构件及声腔的声压贡献率，探讨了采用加设横隔板的减振降噪效果，分析得到以下结论：

(1) 在40～125 Hz范围内，考虑声腔效应的噪声计算值较不考虑声腔的值更接近实测值，采用封闭箱梁模型具有较好的准确性，在计算箱梁噪声时应考虑声腔的影响。

(2) 腔内声腔共鸣对腔外噪声的影响不能忽略，声腔对近场噪声贡献量达42%，对远场噪声贡献量达22.4%。顶板振动对总噪声的贡献率随着测点距离的增大而增大。

(3) 采用加设横隔板的方式能有效的减小声腔内声压和顶板振动噪声，进而降低了箱梁空间结构噪声，加设横隔板是一种切实可行的减振降噪措施，采用两个端横隔板加三个中横隔板的形式比较经济、有效。

(4) 采用FE-SEA混合法能大幅的提高计算效率，与其他方法例如有限元法动辄几个小时的计算时间相比，混合FE-SEA法计算同等模型只需几十分钟，计算效率比较高。