整合教材资源 优化习题设计

彭晓丹

【摘 要】数学习题是课堂教学的重要组成部分，它不但能帮助学生巩固、熟练、活化基础知识，加深他们对数学知识的理解，而且是培养学生数学思维的重要载体。“三角形内角和”练习课的习题如何选择才能更好地按认知规律组织学生进行训练，发展学生的数学思维？教师可以对“三角形内角和”不同教材的习题从习题类型、习题数量和习题异同点三方面进行比较分析，从而为练习课的习题优选提供启示。

【关键词】教材比较；练习课；习题设计；三角形内角和

数学习题是课堂教学的重要组成部分，它不但能帮助学生巩固、熟练、活化基础知识，加深他们对数学知识的理解，而且是培养学生数学思维的重要载体。习题设计要能体现出练习的价值，为学生的学习提供帮助。本文以现行小学数学各版本中“三角形内角和”一课为例，对其中的习题部分进行比较分析，以了解不同教材的编写特点，为练习课的习题设计提供参考，并在此基础上来谈练习课的习题优选。

一、现行不同教材的习题比较

（一）进行比较的教材

本文试图对人教版、浙教版、苏教版、青岛版、北师大版、西南师大版这六套小学数学现行教材中“三角形内角和”这一内容所在单元涉及的与“三角形内角和”有关的习题进行整理，并从习题类型、习题数量和各版本习题的异同点三个方面进行比较研究。

（二）习题的类型

根据习题的功能，我们将各个版本设计的习题类型分为如下3类。

1.基础型

①根据“三角形内角和等于180°”这一性质进行简单计算。已知三角形其中两个角，求第三个角。②明确三角形内角和与三角形的形状无关。

2.综合型

综合利用“三角形内角和”“三角形分类中特殊三角形的性质”来解决问题。

3.探究型

①用“三角形内角和”说明一个三角形中最多只有一个直角、一个钝角。②探索多边形的内角和。

（三）习题数量对比分析

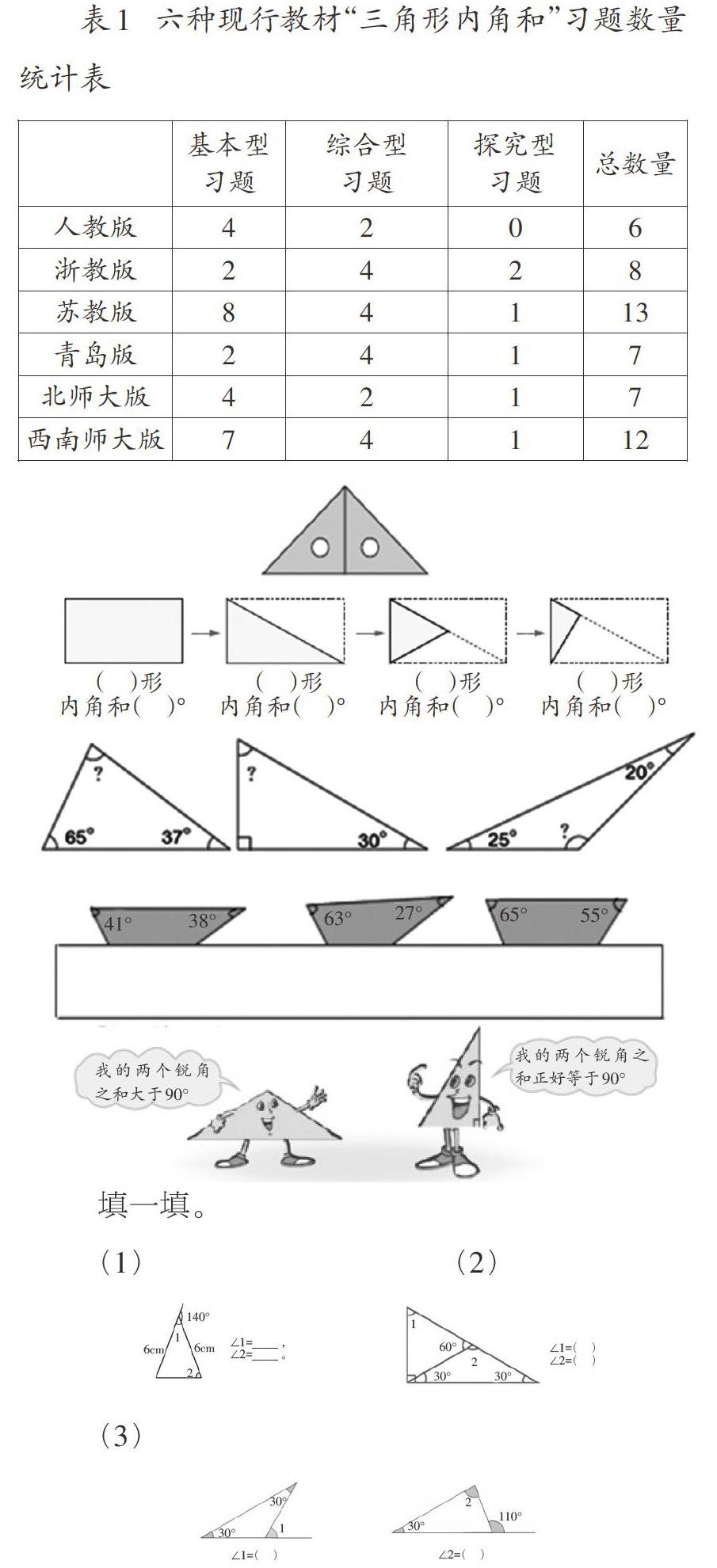
从表1中可以看出：

第一，苏教版在这一单元涉及“三角形内角和”的习题数量最多，西南师大版次之，这两个版本的基础型习题数量也是明显多于其他版本教材的。因为这两个版本教材安排上是先上“三角形的内角和”，再上“三角形的分类”，故在“三角形内角和”课后安排了一定数量的基础性习题。

第二，浙教版、青岛版基本型习题最少，重视综合型习题和探究型习题，注重让学生建立知识间的联系，培养学生灵活运用所学知识解决问题以及进行说理、推理的能力。浙教版的探究型习题是最多的。

第三，人教版、北师大版的习题数量安排相仿。特别说明，因为人教版中“四边形内角和”一课单独作为例题，在该节课后探索五边形、六边形、七边形……内角和，故在习题统计时未将多边形的内角和作为“三角形内角和”的习题，因而人教版“三角形内角和”的探究型习题数量为0。

（四）各版本习题的异同

从表2中可以看到各版本“三角形内角和”习题考查目标有以下异同点。

1.相同点

（1）都有直接应用“三角形内角和是180°”这一性质来计算求解的基础性习题。已知三角形中两个内角的度数，利用“三角形内角和是180°”，求出第三个角的度数。这类习题强化学生对“三角形内角和等于180°”的认识，掌握求三角形中未知角度数的思考方法。并且其中均有涉及“已知一个直角三角形的一个锐角，求另一个锐角的度数”，尽可能让学生掌握直接用90°减去已知锐角的度数，求出另一个锐角的度数这一简便算法，培养学生灵活运用所学知识解决问题的能力。

（2）都有综合利用“三角形内角和的性质”和“三角形分类”的知识来解决问题的习题。

主要类型有：根据等腰三角形中已知角（底角或顶角）的度数，求未知角（顶角或底角）的度数；求等边三角形的内角；已知三角形其中2个内角，判断是什么类型的三角形。这样的习题巩固特殊三角形的特征，又增强了“三角形内角和性质”的运用。

2.不同点

（1）在对“三角形内角和是180°”的含义的考查上有所不同。

人教版安排了“把1个大三角形分割成2个小三角形，求每个小三角形的内角和”的习题。苏教版安排的习题有“用两块完全一样的三角尺拼一个三角形，求拼成的三角形内角和度数”“将正方形不断对折成等腰直角三角形，求三角形的内角和”“用两块完全一样的三角尺拼内角和是180°的图形”。北师大版安排的习题有“把两个相同的三角尺分别拼成一个四边形和一个三角形，先想、再量、后算它们的内角和”“将长方形纸对折剪三角形，再将大三角形不断剪小，使其形状与大小不断变化，填写三角形内角和”。西南师大版安排了“把两块完全一样的三角板，拼成一个三角形，求三角形的内角和”的习题。

这四个版本均有涉及帮助学生进一步理解“三角形内角和是180°”的含义的习题，体会三角形的内角和与三角形的形状、大小无关，帮助学生积累一些图形变换的经验。其他两个版本没有涉及。

（2）在梳理“三角形内角和是180°”探索过程的考查上有所不同。

北师大版结合对课上探索活动的回顾，交流体会，明晰三角形内角和是180°，总结解决问题的方法。其他版本没有涉及。

（3）在对学生综合运用所学知识进行推理这一能力的考查上有所不同。

浙教版安排了“思考一个三角形中是否可能有两个直角或钝角”的习题。北师大版安排了判断“钝角三角形两个锐角之和大于90°”和“直角三角形两个锐角之和等于90°”这两句话是否正确的习题。

这两个版本习题中都有综合运用“三角形内角和”“三角形分类特征”等所学知識进行推理，提高学生解决问题的能力的题目。其他版本没有涉及。

（4）在对四边形或者多边形内角和推导的考查上有所不同。

浙教版安排了“把一个三角形截去一个内角后，变成一个四边形，求四边形内角和” 的习题。苏教版安排了“用两块完全相同的三角尺拼内角和分别是180°、360°的图形”的习题。青岛版安排了“根据三角形内角和是180°，推算长方形和正方形内角和”的习题。西南师大版安排了“根据三角形、四边形的内角和，推导五边形、六边形内角和”的习题。

浙教版、苏教版、青岛版在习题中均有根据三角形内角和是180°，观察、推算出四边形的内角和。西南师大版在习题中分析多边形的边数与三角形个数之间的关系，体会计算多边形内角和的一般方法，不归纳多边形内角和的公式。人教版中“四边形内角和”作为例题教学已在前面说明。苏教版 “多边形内角和”作为“综合实践课”进行教学，所以习题中只有一道四边形的内角和。北师大版没有涉及四边形或者多边形的内角和的习题。

二、对练习课的习题优选的启示

通过对以上六个版本不同教材习题的分析与比较，可以为练习课的习题优选提供如下启示。

（一）基础型练习的安排，应该强化学生对“三角形内角和等于180°”的认识，掌握求三角形中未知角度数的思考方法

比如，已知三角形中两个角的度数，利用“三角形内角和是180°”，求出第三个角的度数或者判断三角形的类型；已知一个直角三角形的一个锐角，求另一个锐角的度数；在三角形的分与合的过程中，求三角形的内角和等。但是此类习题安排时要注意适量，注意习题形式的改变，培养学生思维的灵活性。另外，无论是三角形内角和性质的探索还是理解，以及探索多边形的内角和，学生对于“内角”概念的理解都非常重要，因此练习课习题设计时要注重学生对于“内角”这一概念的理解。

（二） 综合型习题的安排，应该培养学生综合运用“三角形内角和的性质”“特殊三角形的性质”等所学知识进行推理，提高学生解决问题的能力

有两个版本的习题涉及学生用所学的知识进行推理、说理能力的培养，这也是我们在练习课上应该加以重视的。比如“根据等腰三角形中已知角（底角或顶角）的度数，求未知角（顶角或底角）的度数”； 思考一个三角形中是否可能有两个直角或钝角。培养学生的语言表达能力，关注学生说理的条理性、逻辑性是数学教学的一个重要方面。在练习课上教师应当适当培养学生说理的能力。“我是怎样做的？”“我为什么这样做？”“这样做的结论是什么？”学生在表达自己的想法和做法的过程中，培养了思维的条理性，明确教材编者的意图。

（三）探究型习题的安排，应该培养学生关注知识的联系，注重学生数学思想的系统性的建构

比如，从学习三角形的内角和到探索四边形的内角和乃至多边形的内角和，由内角拓展到外角，有利于学生感受图形内部角之间的联系，帮助学生将所学知识系统化。将三角形内角和的性质和三角形的分类进行综合练习，将三角形内角和与图形特征建立起联系，也体现了知识的内在联系。教师在教学时，应当有意识地培养学生关注知识的联系，注重学生数学思想的系统性的建构。

三、“三角形内角和”练习课的习题优选

心理学研究者指出，知识只有组织成系统，才会被学生迅速、准确而牢固地记忆并迁移，而这个系统应该是有序的、有层次的。所以在设计练习题时先模仿，再变式，然后综合应用，最后再进行开放题的探究，注重知识的灵活运用，发散学生的思维。另外，练习题设计应尽可能注重与生活的联系，在学生生活经验的基础上设置相关练习题，提高练习题的生活味，让学生体会到数学与生活的密切联系。这样，学生才能更加深刻地理解所学知识，保持学习的动力。

（一）基础型习题的优选

1.回顾思维历程，加深性质理解

（1）三角形内角和等于多少？我们是用什么方法进行探索的？

（设计意图：通过对三角形内角和探索活动的回顾，交流体会，明晰三角形内角和是180°，总结解决问题的方法。）

（2）①如图，用两把完全相同的三角尺拼成一个三角形，拼成的三角形内角和是多少度？

②用一张长方形纸剪一剪，再填一填。

（设计意图：三角形分与合的过程中，三角形的形状和大小不断变化，加深对三角形内角和性质的理解，激活学生的思维。）

2.应用性质计算，提高计算能力

（1）下面每组角是同一个三角形的内角吗？如果是，请指出它是什么三角形。

①∠1=120°，∠2=30°，∠3=30°

②∠1=90°，∠2=40°，∠3=50°

③∠1=85°，∠2=55°，∠3=50°

④∠1=55°，∠2=60°，∠3=60°

（設计意图：应用三角形内角和性质进行判断，让学生明确要构成一个三角形，三个角加起来的度数必须是180°。此题灵活应用“三角形内角和是180°”来解决问题，提高三角形内角和性质的应用能力。）

（2）算出下面未知角的度数。

（设计意图：利用“三角形内角和是180°”，求出第三个角的度数，强化学生对“三角形内角和等于180°”的认识，掌握求三角形中未知角度数的思考方法。安排“已知一个直角三角形的一个锐角，求另一个锐角的度数”，尽可能让学生掌握直接用90°减去已知锐角的度数，求出另一个锐角的度数这一简便算法，培养学生灵活运用所学知识解决问题的能力。）

（3）你能根据每个三角形中已知的两个锐角的度数，判断各是什么三角形吗？

（设计意图：灵活运用三角形内角和的性质，把三角形两个锐角的和与90°进行比较，快速进行判断，培养解题思维的灵活性。）

（二）综合型习题的优选

1.应用性质解题，培养发散思维

（1）有一个等腰三角形的风筝，它的底角是30°，它的顶角是多少度？

（2）埃及金字塔的四个侧面的形状都是等腰三角形，每个等腰三角形的顶角约是52°。金字塔每个侧面的底角是多少度？

（3）已知等腰三角形的一个内角是40°，它的另外两个内角是多少度？

变式：已知等腰三角形的一个内角是60°，它的另外两个内角是多少度？

（设计意图：根据等腰三角形中已知角（底角或顶角）的度数，求未知角（顶角或底角）的度数，特别是有一个角是60°的等腰三角形的内角的度数。这样的题目综合利用“三角形内角和的性质”和“三角形分类”的知识来解决问题，帮助学生进一步巩固等腰三角形和等边三角形的特征，培养灵活运用所学知识解决问题的能力，培养逻辑思维，提高解题思维的灵活性。）

2.应用性质说理，提高推理能力

（1）它们说得对吗？

（2）想一想：一个三角形中可能有两个直角或钝角吗？为什么？

（设计意图：运用三角形内角和是180°进行分析推理，加深对“一个三角形中至少有两个锐角”的理解，培养学生的逻辑性思维和数学语言表达能力。在解决数学问题和同伴交流的过程中，发展数学交流的能力，感受成功的喜悦，增强学好数学的信心。）

（三）拓展型习题的优选

1.综合应用性质，培养逻辑思维

填一填。

（设计意图：这些题目具有较强的综合性，学生要灵活运用所学知识解题，既巩固三角形内角和的性质、等腰三角形的特征、平角等相關知识，还适度拓展外角的知识，提高思维的有序性和灵活性。在拓展应用的过程中，体会三角形内角和及相关数学方法的价值，注重数学思想系统性的建构，进一步产生对数学的好奇心，感受数学活动的挑战性和趣味性，增强数学学习的兴趣。）

2.经验迁移，系统建构数学思想

请用你喜欢的方法来探索五边形的内角和。

想一想，如果是六边形、七边形呢？

（设计意图：根据三角形内角和是180°，利用转化思想求解，推算多边形的内角和，培养学生的探究推理能力。在类比迁移的过程中，积累探索和发现数学规律的经验，感悟数学思想方法，培养学生的发散性思维和探究推理能力。）

这些习题的设计，注重学生知识的理解与灵活运用，培养学生的逻辑思维和数学语言表达能力，注重数学思想习题性的建构。习题设计时关注学生的思维与思考，让学生自己在操作中感悟，在比较中选择，从而成为一个“会想”的人。数学不单单是“会做”，还要让学生在学习中感受到喜悦。

总之，对不同教材的习题进行比较，博采众长，可以便于教师更好地整合教材资源，服务于教学设计。

参考文献：

[1]陈永明名师工作室.数学习题教学研究[M].上海：上海教育出版社，2010.

[2]人民教育出版社.义务教育教科书数学教师教学用书（四年级下册）[M].北京：人民教育出版社，2014.

[3]张天孝.义务教育小学实验教科书数学教学参考书（四年级下册）[M].杭州：浙江教育出版社，2012.

[4]南京东方数学教育科学研究所.义务教育教科书数学教师教学用书（四年级下册）[M]. 南京：江苏凤凰教育出版社，2014.

（浙江省台州市白云小学 318001）