机械臂末端轨迹跟踪的自适应鲁棒控制

张 卓 张 程

（1广东科学技术职业学院，广东珠海，519041；2吉林大学珠海学院，广东珠海，519041）

0 引言

在机械臂轨迹跟踪控制过程中，常规控制方法具有收敛缓慢、控制精度低的问题，而且还要求系统参数必须明确已知，如果参数不确定，比如，机械臂抓取一个未知负载，那么常规控制器则不能保证实现理想性能[1-2]，但自适应鲁棒控制律可以解决上述问题。在模型和参数不确定的情况下，自适应鲁棒控制律仍能保持机械臂在稳定性、跟踪误差或其他指标方面的性能表现[3-5]。

本文利用SolidWorks软件进行机械臂结构的自主设计，采用Lagrange-Euler法建立机械臂的动力学模型，设计自适应鲁棒控制律及相关控制参数，并在Ⅰ、Ⅱ、Ⅲ及Ⅳ四个象限工作空间内进行跟踪控制实验，实验证明，本方法具有明显优于常规控制器的跟踪控制性能。

1 机械臂结构设计及动力学分析

1.1 机械臂结构设计

本文利用SolidWorks自主设计一套仿人机械臂结构，并建立机械臂的三维模型[6]，适用于物体追踪、检测、切割以及扫描等作业。图1为仿人机械臂结构设计，其具有肩关节（设计将肩关节固定在外轴机构上以扩展该机械臂的作业范围）、肘关节、腕关节（末端执行器），由电机驱动，可以实现3个自由度运动。其中，肩关节运动范围为-180°～180°，肘关节运动范围为-170°～170°，腕关节运动范围为-90°～90°。标称物理结构参数如表1所示。

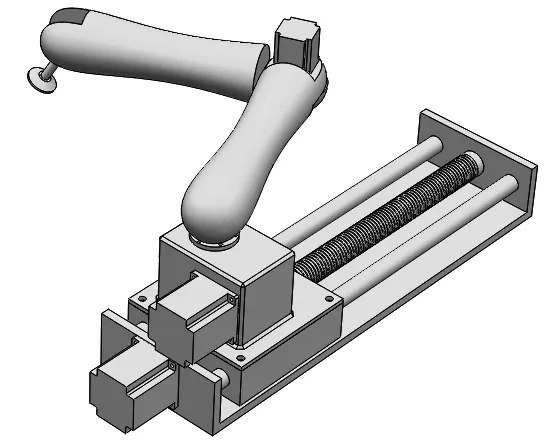
图1 仿人机械臂结构设计

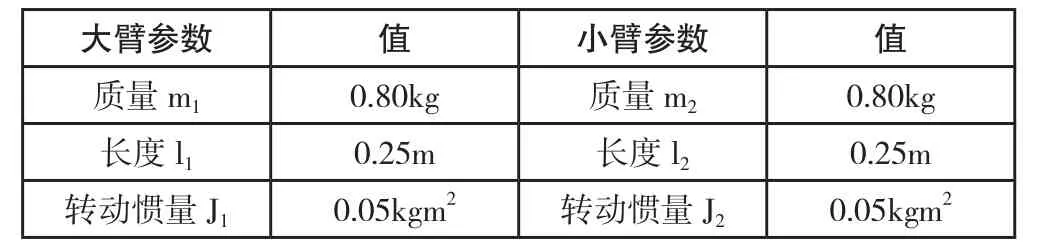
表1 仿人机械臂标称结构参数

1.2 机械臂动力学分析

本文采用Lagrange-Euler法建立机械臂动力学方程。仿人机械臂的运动坐标如图2所示，目标工作空间为x轴和y轴所构成的平面，考虑腕关节要保持相对该平面的近似固定位姿，故在Ⅰ、Ⅱ、Ⅲ及Ⅳ四个象限工作空间内分析其轨迹规划控制，并建立工作空间关节末端节点直角坐标( qx,qy)的动力学模型。

图2 机械臂运动坐标示意图

机械臂末端在工作空间中的期望坐标位置为[7]：

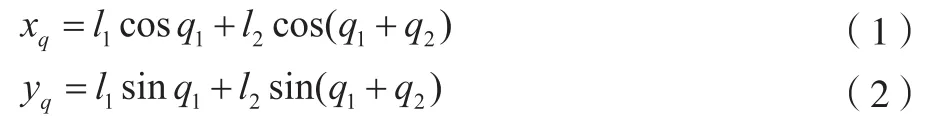
其中，根据D-H法则，q1表示肩关节x0绕z0轴转向x1的角度；q2表示肘关节x1绕z1轴转向x2的角度，z0轴和z1轴均垂直于作业平面[7]。求二者的平方和得：

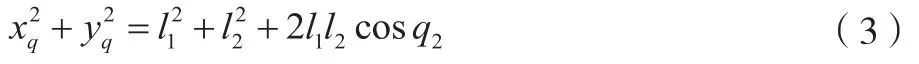
从而可解得：

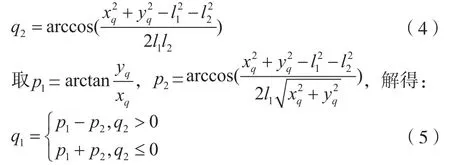
假设机械臂的期望关节位置为 ，期望速度为 ，期望加速度为 ，则机械臂的运动可由式（6）描述：

2 自适应鲁棒控制器设计

本文采用鲁棒模型参考自适应控制方法（基于Lyapunov直接法），控制目标为在存在参数不确定和位置非线性摩擦特性的情况下，使跟踪误差趋于0[8-10]，以确保机械臂的控制系统具有良好的运动特性。

根据式（6）设计逆向动力学补偿为[7]：

将式（7）代入方程（6），得：

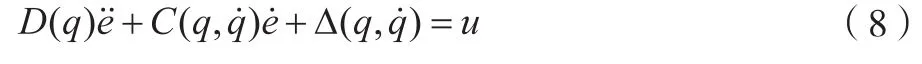
定义辅助信号 ：

其中，a ＞0。

则式（8）可表示为：

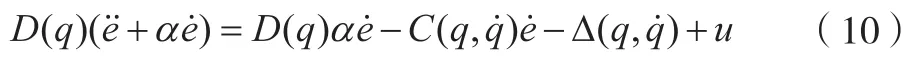
即：

取：

则式（12）可表示为：

鲁棒控制律设计为：

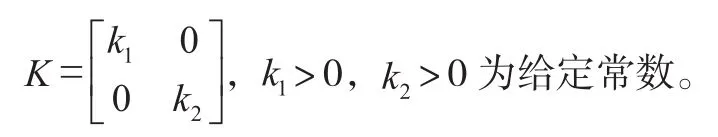
3 机械臂末端轨迹跟踪仿真

在初始位姿固定的条件下，本文分别在Ⅰ、Ⅱ、Ⅲ及Ⅳ四个象限工作空间内设计目标轨迹，利用Simulink建立仿人机械臂控制系统模型进行轨迹规划控制，验证自适应鲁棒跟踪控制效果，并与常规控制下的轨迹跟踪效果进行比对，得到实验数据及结论。

3.1 四象限轨迹跟踪仿真分析

本文采用S函数输入目标轨迹函数，选取Ⅰ、Ⅱ、Ⅲ及Ⅳ象限工作空间内目标运动函数进行轨迹跟踪实验，目标轨迹生成指令如下：

function sys=mdlOutputs(t,x,u)

xd=0.2*cos(pi/2*t)+0.2; %第Ⅰ象限

yd=0.2;

xd=0.2*cos(pi/2*t)-0.2; %第Ⅱ象限

yd=0.2;

xd=-0.2; %第Ⅲ象限

yd=0.2*cos(pi/2*t)-0.2;

xd=0.2; %第Ⅳ象限

yd=0.2*cos(pi/2*t)-0.2;

控制律增益取 = =65， =0.001，得到在Ⅰ、Ⅱ、Ⅲ及Ⅳ四个象限工作空间内的轨迹跟踪示意图及关节位置跟踪结果如图3-图10所示。

由图3可见，当目标轨迹在第Ⅰ象限工作空间内时，机械臂能迅速跟踪至目标轨迹，路径合理且冗余轨迹少。由图4可见，机械臂各关节的位置跟踪准确，运动位置与目标位置一致且跟踪速度快。

以同样定性方法分析其他象限情况，如图5-图10所示，与第Ⅰ象限轨迹跟踪的情况类似，均可得到结论：鲁棒控制方法控制速度快、路径跟踪合理且位置跟踪准确。

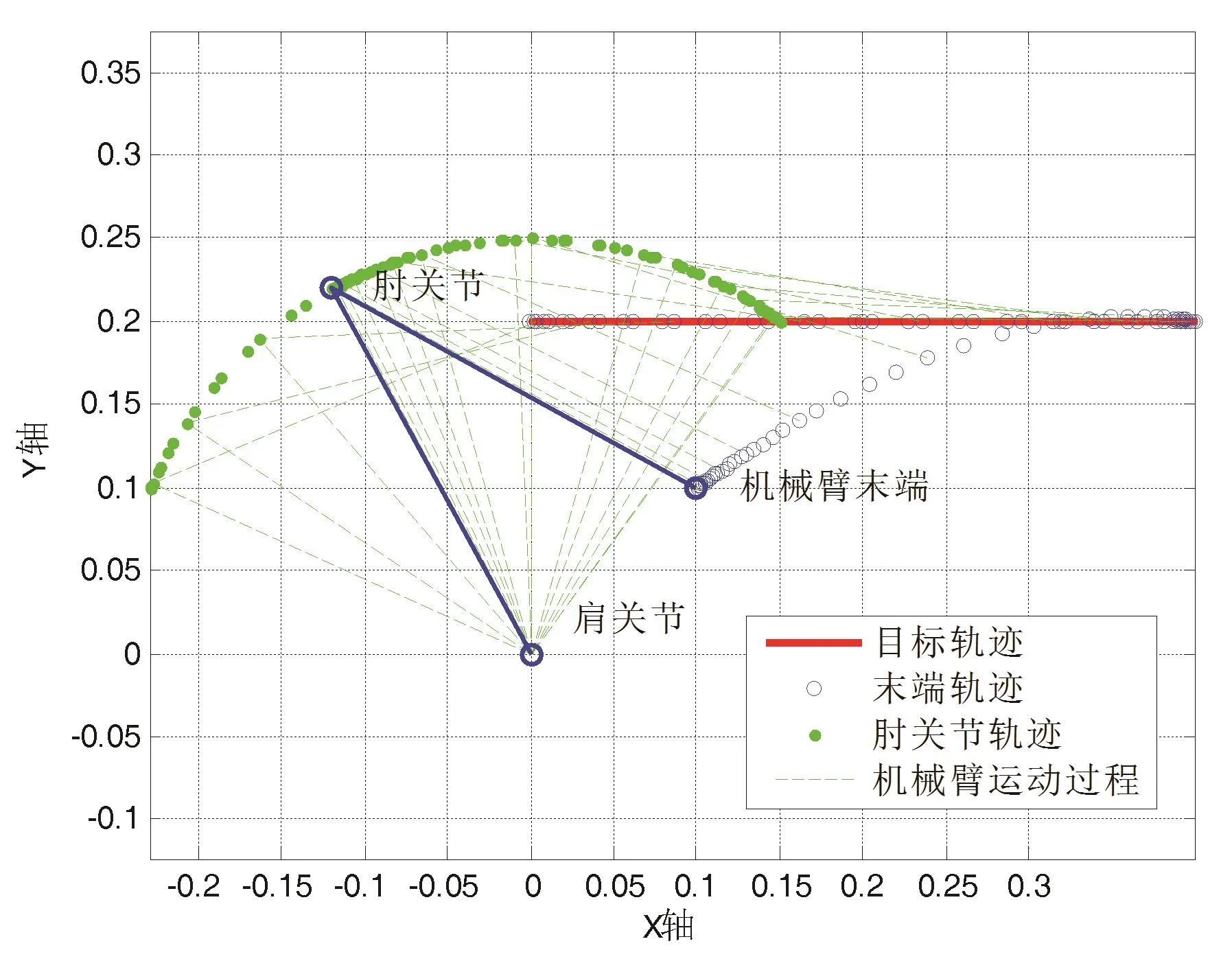
图3 轨迹跟踪示意图（第Ⅰ象限）

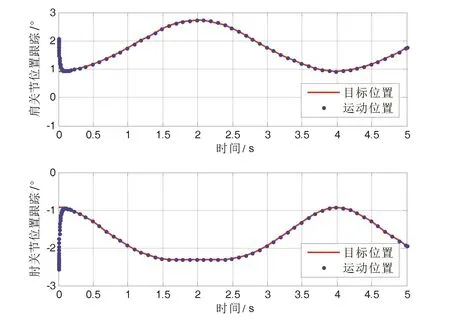
图4 机械臂关节位置跟踪（第Ⅰ象限）

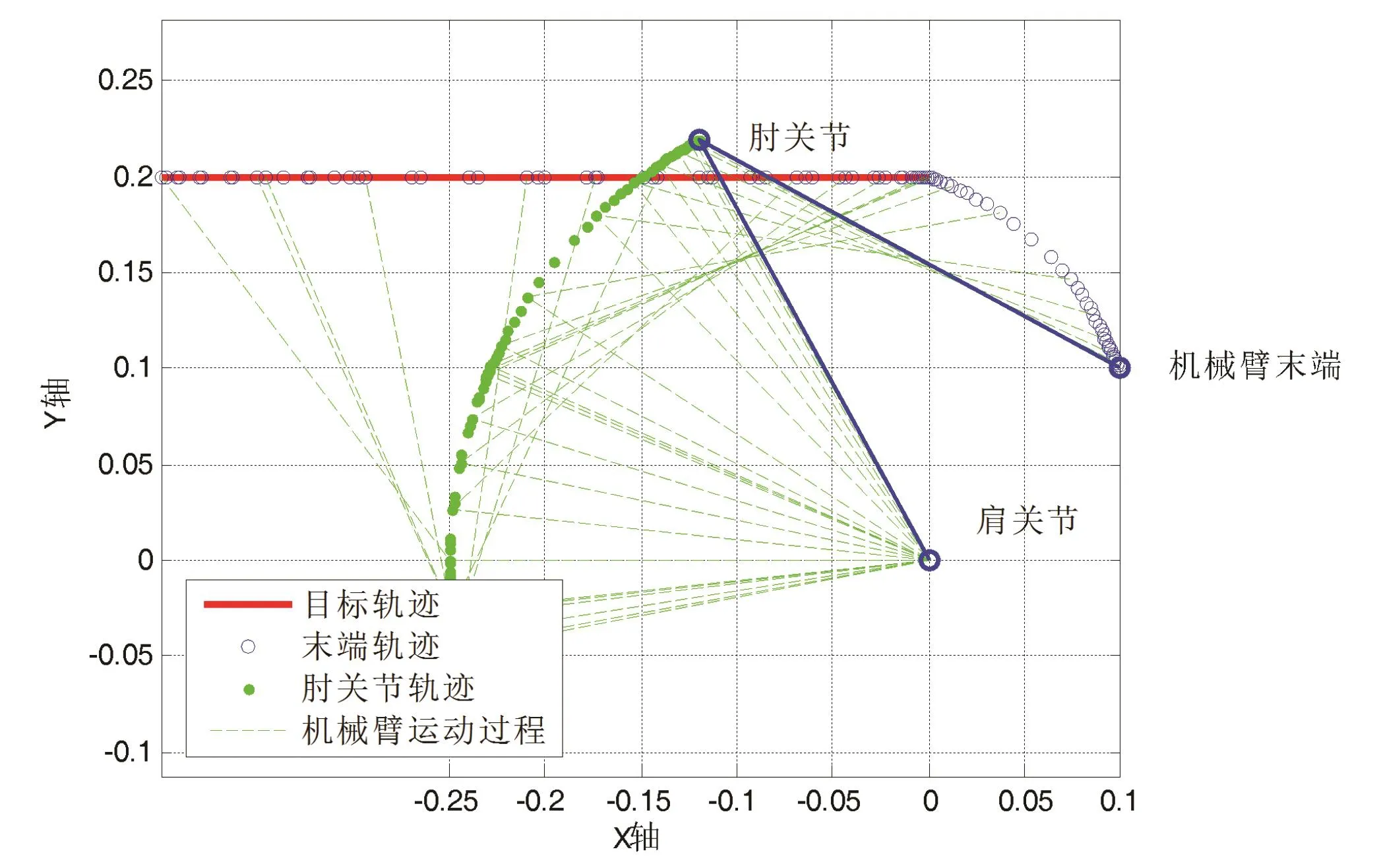
图5 轨迹跟踪示意图（第Ⅱ象限）

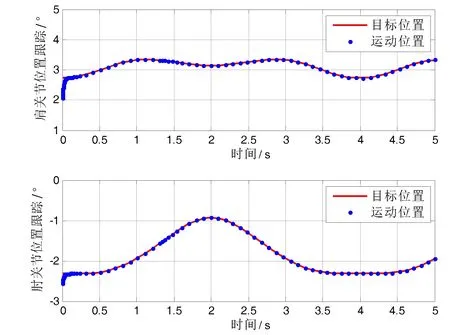
图6 机械臂关节位置跟踪（第Ⅱ象限）

图7 轨迹跟踪示意图（第Ⅲ象限）

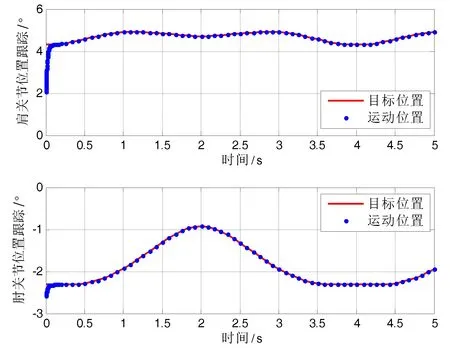
图8 机械臂关节位置跟踪（第Ⅲ象限）

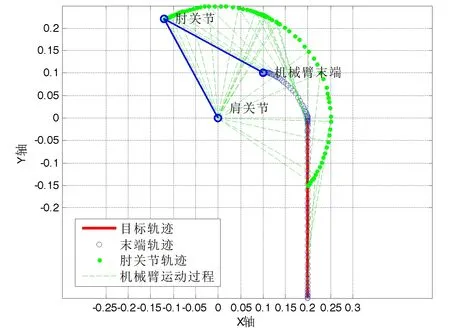
图9 轨迹跟踪示意图（第Ⅳ象限）

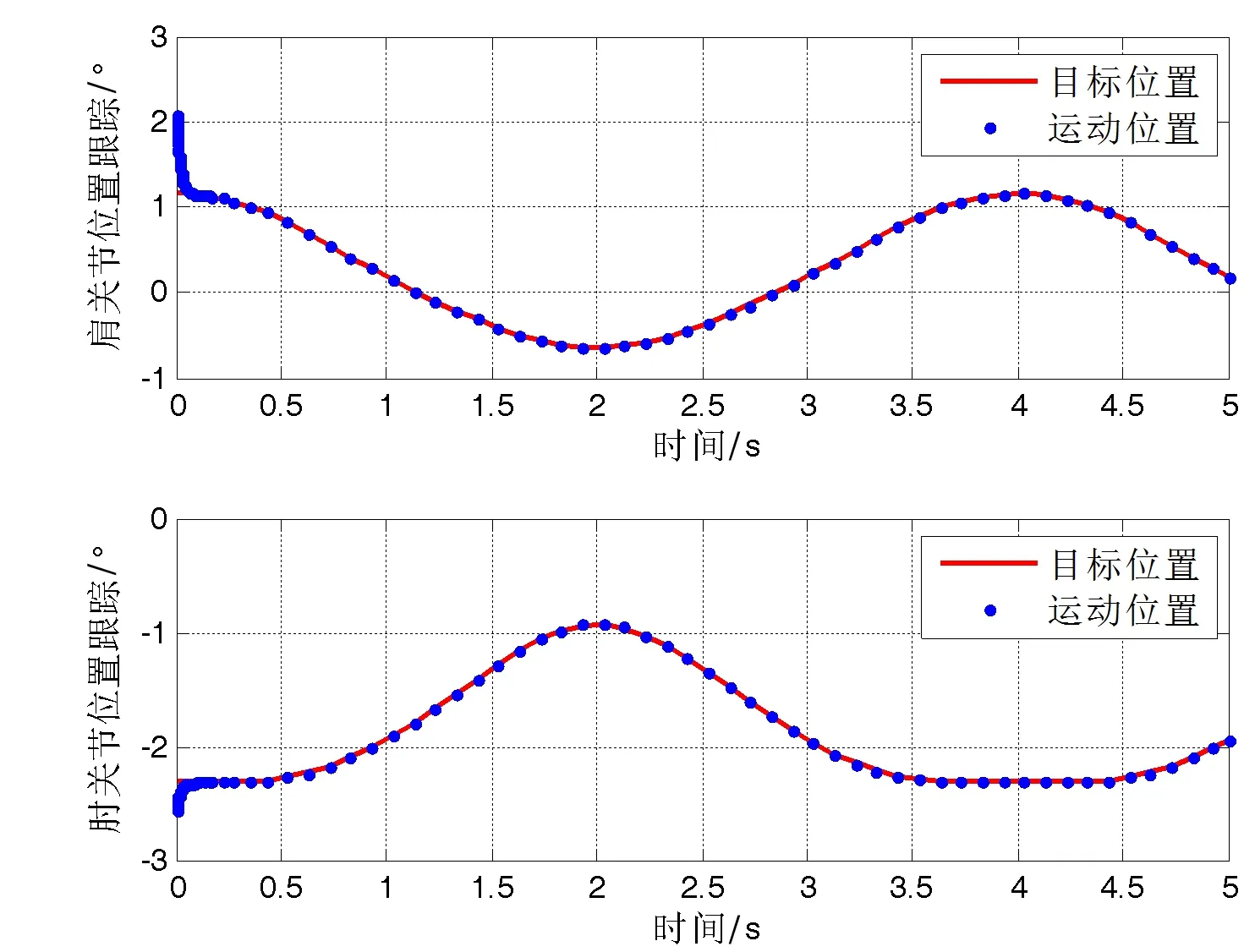
图10 机械臂关节位置跟踪（第Ⅳ象限）

3.2 四象限轨迹跟踪误差分析

针对上述仿真结果，本文进一步分析轨迹跟踪误差，分别分析Ⅰ、Ⅱ、Ⅲ及Ⅳ四个象限工作空间内的关节位置跟踪误差，将本鲁棒控制方法同常规控制方法误差进行对比，得到图11-图14的轨迹跟踪误差分析。

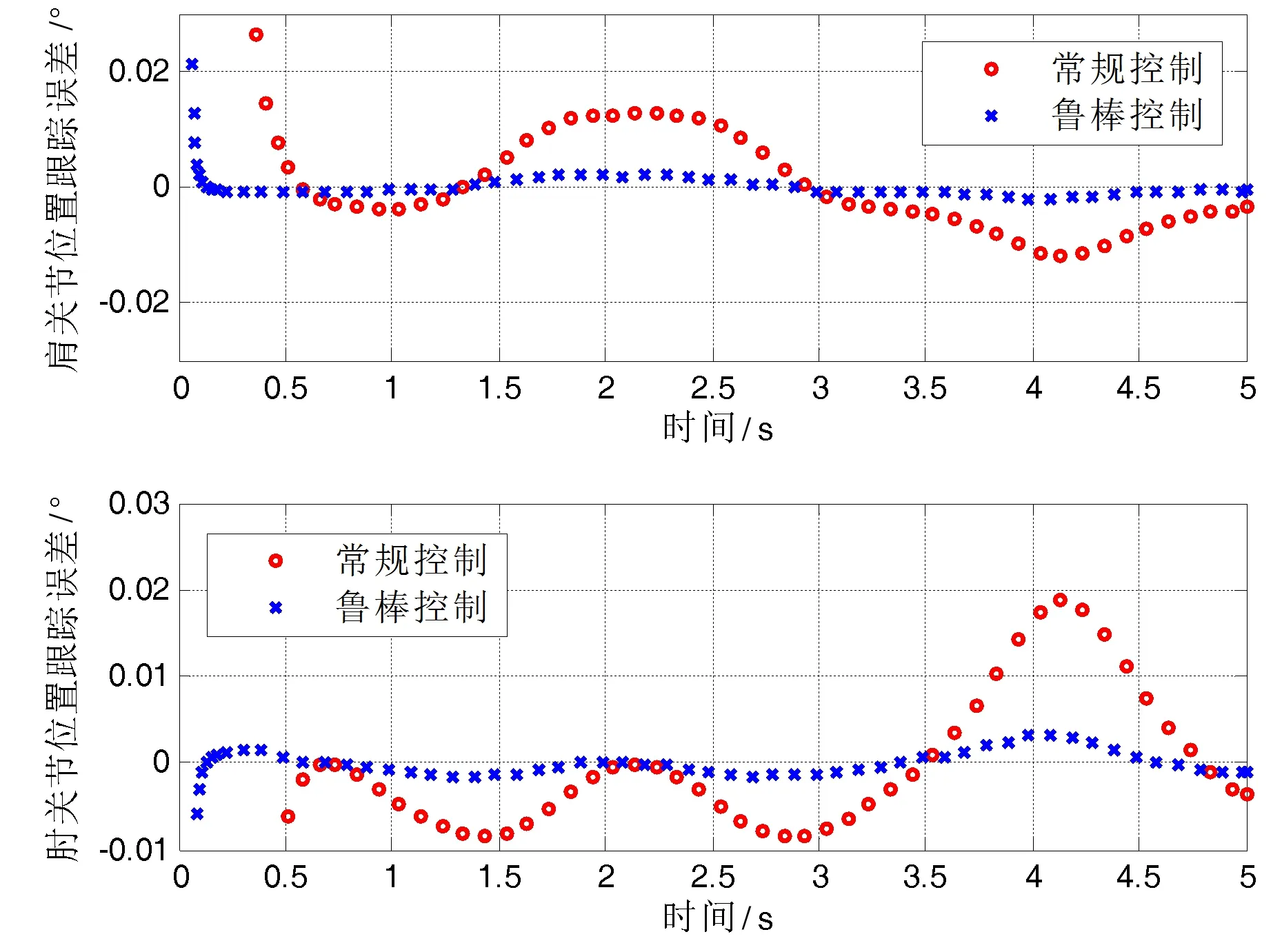
图11 轨迹跟踪误差分析（第Ⅰ象限）

图12 轨迹跟踪误差分析（第Ⅱ象限）

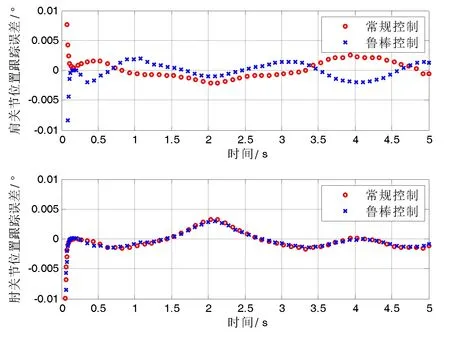
图13 轨迹跟踪误差分析（第Ⅲ象限）

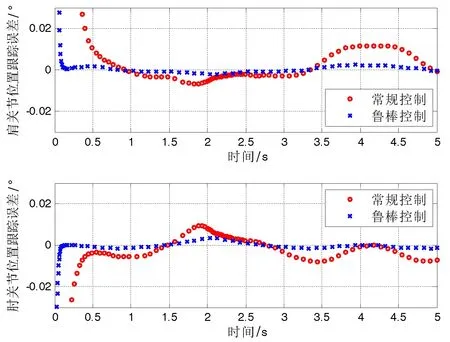
图14 轨迹跟踪误差分析（第Ⅳ象限）

由图11可见，常规控制方法的收敛时间长且控制精度差，在4.1s时的肘关节位置误差达到0.019°，收敛时间近0.5s；而鲁棒控制方法最大误差为0.001°，收敛时间为0.2s。相对于常规控制器，鲁棒控制的收敛速度提升60%，位姿跟踪最大误差精度提高约95%。这说明，在第Ⅰ象限内，鲁棒轨迹跟踪控制效果优于常规控制方法。

以同样量化方法分析其他象限，如图12-图14所示，实验结果与第Ⅰ象限轨迹跟踪的情况类似，均可得到结论：与常规控制方法相比，鲁棒控制方法收敛时间短、跟踪速度更快。

综上可得，在第Ⅰ、Ⅱ、Ⅲ及Ⅳ四个象限工作空间内，鲁棒轨迹跟踪控制在跟踪性能和响应速度上均优于常规控制器，能够保证机械臂系统达到更好的跟踪性能。

4 结论

本文利用SolidWorks自主设计了一套带有外轴的机械臂结构，以及设计了一种自适应鲁棒控制策略，并采用Simulink进行机械臂控制系统模型设计，最后对第Ⅰ、Ⅱ、Ⅲ及Ⅳ四个象限工作空间内的机械臂末端鲁棒轨迹分别跟踪控制仿真。实验结果表明，相比常规控制器，该自适应鲁棒控制方法能够更加快速、准确地控制机械臂的末端轨迹，具有较好的可行性及一定的工程参考性。