基于三维可视化技术的多层矿床建模及优化研究
李普山 李伟波 冯智莉
(武汉工程大学计算机科学与工程学院 湖北 武汉 430000)
0 引 言
罗布泊盐湖是我国超大型的含钾卤水矿床,盐湖由东向西宽90千米,从南到北长115千米,是世界上最大的干盐湖之一。其卤水属硫酸镁亚型卤水,赋存有钾、镁、钠等成分,其品位超过工业品位,其中钾盐近期储量为1亿吨,远景储量为2.5亿吨[1]。科学规划盐田年度的采收方案、优化采盐船的开采路径、保证硫酸钾厂吃矿的含钾品位,对合理开发、高效利用不可再生盐田资源,提高企业经济效益,实现企业可持续发展具有重要意义。而采收方案的基础就是矿床模型,因此,如何准确高效地构建矿床模型是科学规划采收方案的关键。
为此,本文提出了一种基于Delaunay三角网和并行计算技术的矿床三维可视化的分层模型。通过对整个盐池进行分层处理来准确反映不同深度矿床的内部情况,同时运用并行技术对数据计算进行并行处理,使得模型生成速度显著提高。
1 问题分析
盐矿开采,实际上是对卤水析出的盐层进行开采,必须知道盐池中的矿量以及属性结构。因此需要在相对固定的时间周期内用测深仪等进行空间数据和属性数据的采集,再选择规则网络结构或不规则三角网TIN(Triangular Irregular Network)建立盐矿的数字高程模型DEM(Digital Elevation Model)。由于卤水受环境条件的因素影响,不同深度盐矿形成的品位和厚度也是变化的,单一的DEM显然无法反映不同深度的真实情况。因此,必须建立多层的DEM,而且每一层是可以揭开以反映盐矿内部情况。另外,即使单一的DEM建模都有大量的数据计算,多层DEM构建过程中如何提高建模效率也是必须重视的问题。
构建可独立分层的DEM模型,可以采用化整为零的思想,根据测深时间的不同,将矿床分成不同的盐层,每一层盐层利用TIN来拟合曲面,再将各层TIN组合起来就构成了整个盐矿[2-6]。这样既可以对矿床内部的结构有所了解,又可以对整个矿床不同位置的品位进行查询,使矿量计算更加准确。
单层DEM的构建采用Delaunay三角剖分算法。经过大量学者证明,在平面内任意给定点集的Delaunay三角剖分具有整体最优的性质,即对于任意给定的平面点集,Delaunay三角划分能够得到整体最优的三角形网格,能够尽可能地避免病态三角形的出现[7]。为了使三角剖分尽可能优化,一般在进行三角剖分时遵循两个准则:(1) 空圆特性,在三角网格中任一三角形的外接圆内都不存在其他的点;(2) 最大化最小角特征,相邻三角形构成的凸多边形的对角线,在交换后,六个内角中最小的内角最大[8]。根据这两个准则形成的三角网格是唯一的,这也是Delaunay三角划分的划分标准。
当前,构建三角网格的算法大致可以分为三类:区域生长法、合并分割法(分治法)和逐点插入法。其中:区域生长法中主要以三角网生长为主,三角网生长法的效率相对较低,虽然改进空间较小,但是实用性很强;合并分割法的效率最高,但是其运用了递归的思想,运行过程会占用大量内存,不能处理大量数据;逐点插入算法比较简单,需要内存空间不大,但是它的时间复杂度相对较高。
每一次采集的空间数据都比较多,同时多层构建DEM运算量急剧加大,在尽量保证系统效率的前提下,本文采用了多线程的并行处理办法,让不同层的数据并行处理,尽可能提高系统效率。
2 方案设计
提出本方案的最终目的是为了能够准确地计算矿量,矿量计算公式为:矿量=体积×品位,故品位和体积是计算矿量的关键。而前文已经提到,受环境条件的因素影响,不同深度盐矿形成的品位不一样,因此需要将整个盐矿分层以便对不同位置的盐矿品位进行处理。
对于盐矿体积计算,这涉及到盐层间的联系(尽管各盐层构网过程相互独立,但在进行体积计算时需要知道相邻盐层对应采样点的过程),计算出单位体积内的矿量后再进行积分求和,从而计算出整个矿床的矿量。因此,要求在每一次数据采集时,采样点的水平面坐标、采样点编号相同,这样相邻两层三角网格将矿体分割成无数小三棱柱,计算每个小三棱柱体积再积分求和得到每个矿层体积,而在进行查找相邻盐层的对应点高程时也会简单很多,从而降低算法难度。
为使三维仿真模型尽可能逼真,每次获取的数据均比较多。其中存在大量数据冗余,而且受测深航线影响,数据分布不够均匀,深度变化小,需要进行合适的处理。为此,本文采用了一种设定影响圆半径的方法剔除部分相似数据,采用误差识别方法剔除异常数据。将采样点集处理之后,对这些散乱点集进行Delaunay三角剖分,即生成Delaunay三角网格。三角网是三维地质建模中的一种常用方法,是按一定规则将离散点拓扑连接成覆盖整个区域且互不重叠的三角形网格。当三角形数量足够多时,可以无限拟合曲面的起伏情况,从而建立了离散点间的空间曲面关系。三角剖分可以根据卤水下盐层的起伏情况来调整三角形的大小和数量,便于浏览三维盐层的矿床模型。
由于每一盐层的采样数据较多,如逐一对每一盐层进行三角剖分会严重影响系统效率,故本文采用了多线程的并行处理的方式,来对各盐层并行处理,以此来提高系统效率。对于多线程技术,核心问题是任务调度,需要从系统的性能评估入手,即从并行线程的规模数、数据竞争、锁竞争、线程安全、存储和数据组织等方面对系统进行分析和优化[9]。一般对共享数据的访问会引发数据竞争,从而导致结果的不确定性。为此,需要将各盐层的采样点划分好,使其相互独立,从而消除数据共享可能引发的数据竞争、锁竞争以及存储问题。并且在程序构造上加强结构化和模块化,从而大大降低了多线程编程的复杂程度。
3 算法实现
根据用户需求,方案的总体工作流程如图1所示。
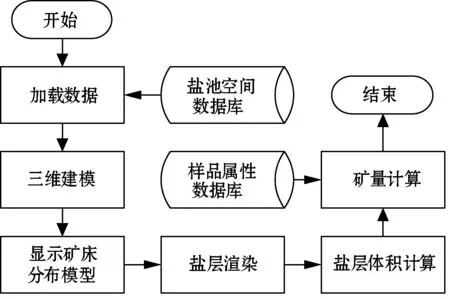
图1 系统总体功能流程图
本方案需要对盐池采样点进行分析,获取采样点的位置信息以及采样点附近盐矿样品的属性(组份、含量、时间),分别建立盐池采样点的空间数据库和属性数据库。根据空间数据库里的三维坐标信息建立卤水下矿床的三维模型并计算出盐层体积,然后利用盐层体积结合属性数据库里的盐矿品位信息计算矿量。
3.1 独立分层数据的组织
根据系统设计方案,本系统数据文件包含两类:图形数据文件和属性数据文件。图形数据文件是可视化的图形文件,本文选用WRL文件作为系统的空间图形数据文件。同时该文件也可用于与外部软件进行交换的接口。属性数据文件组织,包含项目数据配置文件、测深仪数据文件以及层样品分析数据文件。其中:项目数据配置文件用来定义初始数据、链接采样数据文件和样品分析数据文件;测深仪数据文件记录的是各采样点的坐标信息以及其编号;层样品分析数据文件记录了各采样点的盐矿品位信息、坐标信息以及采样时间。
为了提高检索效率,方便存储和维护盐池信息,需要建立相关数据库。表1、表2是根据分层模型数据组织建立的数据库部分情况。表1是按盐层建立的数据库盐层表;表2是数据库采样点表,存储的信息是盐层里面的采样点信息。

表1 数据库盐层表

表2 数据库采样点表
3.2 基于三角网生长法的Delaunay三角剖分
本文采用的是三角网生长法,相对于逐点插入法,不需要进行大量定位三角形的操作; 相对于分割合并算法,生长法也没有大量的搜寻子集边集、并网的操作[10-11]。其基本思想为:以一个三角形为初始三角网,逐渐向外寻找离该三角网各条边最近的点,与对应边组成新的三角形,加入到三角网中形成新的三角网。在生长过程中,要随时对已经生长好的三角网进行拓扑结构检测,确定三角网中各边之间的关系,同时判断生长过程是否终止。其具体算法如下:
(1) 在平面点集中选取任意一点(尽量选择平面点集中间区域的点),寻找离该点最近的点,形成线段,并以此线段作为定向基线。
(2) 根据Delaunay三角形的判别标准,将离基线两端点距离之和最小的点作为新三角形的第三点,并以此确定新三角形。
(3) 把新三角形的两条边(新三角形中除去原基线的两条边)作新的基线。
(4) 重复(2)、(3),直到所有基线都被用过为止。
其具体构网流程如图2所示。
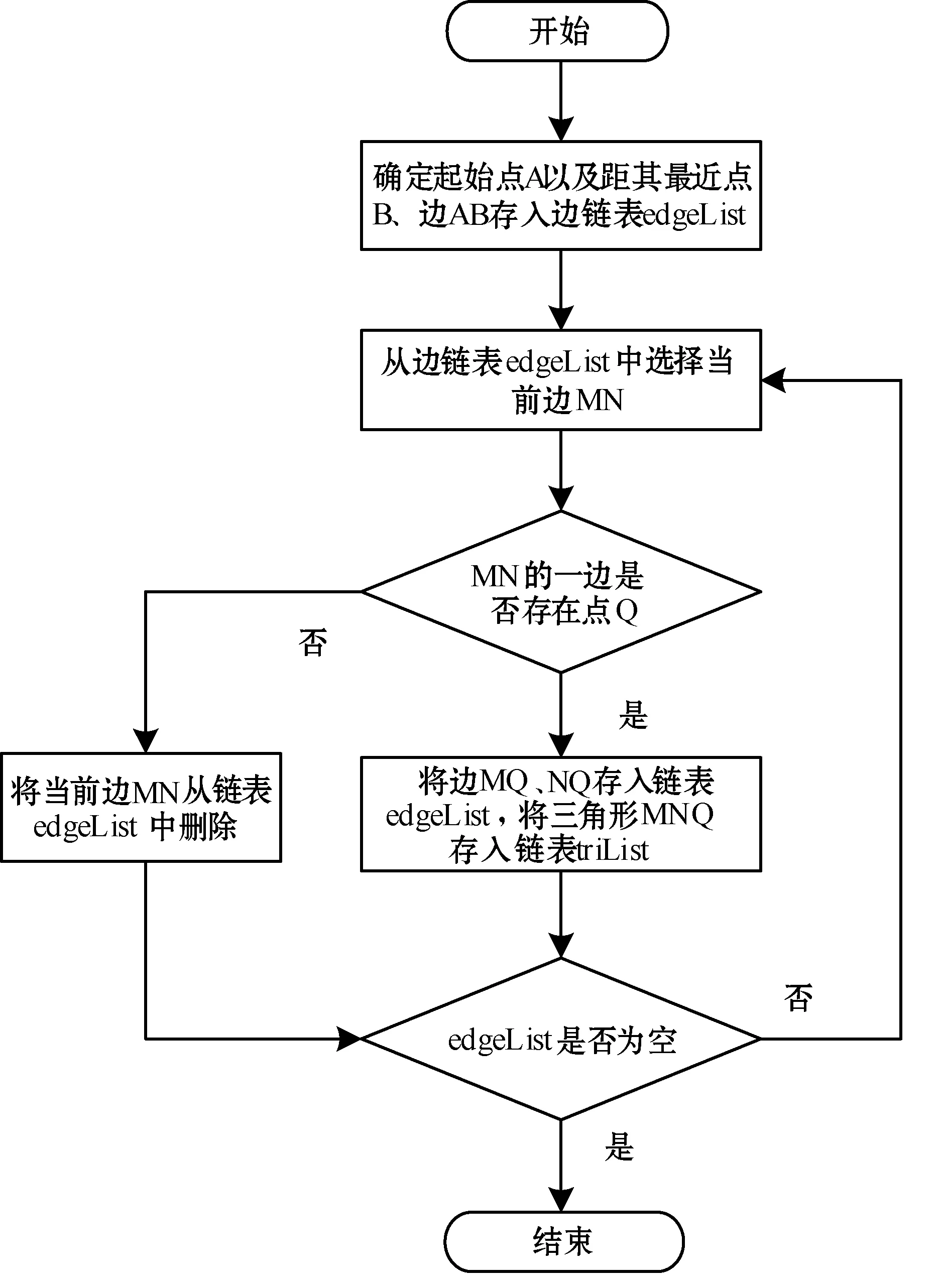
图2 Delaunay三角剖分三角形生长法构网流程图
Delaunay三角剖分构网过程复杂,算法代价较大。因此,本方案利用多线程的并行化思想,在同一坐标系下,让各个盐层的离散点集并行构建三角网格,完成卤水下矿层的三维曲面仿真。
3.3 基于多线程的并行化构网
并行线程并不是规模越大,性能越好。运用多线程是为了更好地利用系统资源,而线程本身也会占用系统资源,如果线程数过多会严重影响程序本身的性能,过少则不能使系统资源得到充分的利用。另外,线程之间切换时新线程所需的数据需要恢复,被切换的线程数据需要保存,这也能直接导致系统性能降低,故需要在线程数与系统性能之间找一个平衡点。
并行处理算法由MFC结合OpenGL以及OpenMP实现。OpenMP提供了对并行算法的高层抽象描述,在程序功能模块中加入专用的pragma来表明意图,由编译器来自动将程序并行化,并在可能发生数据冲突之处加入同步互斥及通信[12-14]。其运用形式示例如下:
#pragma omp parallel for schedule(dynamic)
//并行调度分配迭代
for(int k=0;k { … tin.createTin();//构网 OutputWrl(sWrlFileName); //生成WRL模型文件 … #pragma omp critical//冲突检查 { … WrltoDatabase(); //将层数据写入数据库 } } 得到的结果为整个矿床内部各盐层的三维结构,如图3所示。 图3 各盐层构网结果图 从图3可以很明显看出矿床的各盐层的三维结构情况,对构网结果进行渲染后的盐层三维模型如图4所示。 图4 矿床分层模型三维显示图 系统有以下三个特性: (1) 一致性,对同一盐层进行多次运行得到的构网结果基本相同,即组成Delaunay三角形的顶点编号一致。 (2) 高效性,利用了多线程的并行化思想,让各个盐层并行构网,大大提高了系统效率。 (3) 真实性,能够较真实地反映卤水下矿床的内部空间结构以及成矿过程。 本方案可以根据从勘探现场获得的测深数据生成盐池矿床分层的三维仿真模型,反映卤水下矿床的内部属性结构,方便用户在进行开矿生产时做出相关决策。本文选择C++作为开发语言,利用面向对象的设计思想,以MFC作为框架,把点、边、三角形分别作为一个新的数据结构以对象的形式进行封装,结合OpenGL的三维图形API,较为真实地实现了对盐层的三维仿真。同时,为了提高系统效率,利用多线程并行处理的思想,结合OpenMP编程,让各盐层并行构网,大大提高了系统效率。表3列出线程数与系统运行时间的对比。 表3 不同线程数与系统运行时间对比 由此可知,利用多线程优化后的程序执行效率比不使用多线程时有显著提高,并且线程数对系统效率影响很大,并不是越多效率越高,当线程数达到一定数目时系统效率反而降低,不能简单通过提高线程数来进一步提高效率。 以该项目中5#光卤石池为例,在相同时间间隔内,前后8次获取了其卤水下地形数据,取部分数据进行实验,得到的结果如图4所示,共8个盐层。通过填充之后能够真实地反映其卤水下的矿床情况,具有真实性。将其中第一个盐层转化为WRL文件格式,其内部结构如下,选取17个点,根据坐标x、y、z排列: 132.777 110 0.625 80.574 99.337 1.875 80.331 40.435 0.875 123.92 46.646 0.875 159.676 40.435 0.375 80.396 10 0 100.69 16.625 0.625 140.102 16.625 0.875 159.782 10.414 1.875 139.891 52.545 0.625 107.395 110 0.875 160 100.373 0.625 80 70.455 0.625 100.69 52.959 0 120.581 85.155 0.375 159.782 70.455 0 80 70.455 0.75 经三角剖分后,得到的三角网格如下:其中正数为三角形的三个顶点编号,-1为标志号。 0, 10, 1, -1 0, 14, 1, -1 0, 11, 14, -1 1, 16, 14, -1 14, 15, 11, -1 1, 12, 16, -1 14, 13, 16, -1 14, 9, 15, -1 11, 8, 15, -1 16, 15, 12, -1 14, 3, 13, -1 16, 2, 13, -1 14, 3, 9, -1 15, 4, 9, -1 15, 4, 8, -1 13, 6, 3, -1 13, 6, 2, -1 9, 7, 3, -1 9, 7, 4, -1 8, 7, 4, -1 3, 7, 6, -1 2, 5, 6, -1 8, 5, 7, -1 6, 5, 7, -1 经多次实验,三角剖分结果基本相同,系统具有一致性。另外,将系统以8个线程同时对8个盐层进行构网,系统效率大大提高。 本文针对盐池卤水下矿床的基本特征提出了一种矿床分层模型的三维可视化方案。详细说明了分层数据结构和基于三角网生长法的Delaunay三角剖分算法构建分层DEM方法,并运用OpenMP的多线程并行处理技术和冲突共享机制,实现各盐层快速生成Delaunay三角网后再组合构建多层DEM。应用结果表明,这是一种分层快速建模的方法,能够比较高效准确地反映矿床内部情况,也为复杂DEM建模提供了一种新的研究手段和方法。

4 应用结果分析

5 结 语

