自动化集装箱码头双轨道吊协调调度分析
梁承姬 陈维斗 崔佳诚
(上海海事大学物流研究中心 上海 201306)
0 引 言
自动化已经成为当今码头持续发展的一种趋势,它的出现可以大幅度提高码头的作业效率。自动化集装箱码头虽然在人工成本和安全性上具有很大优势,但是对码头设备的调度控制提出了更高的要求。在自动化集装箱码头中,由于各种码头设备需要联合调度,双小车岸桥(STS)、AGV、以及轨道吊(ARMG)等设备在作业时都存在各种协调问题,其中以ARMG的协调调度问题最为突出。与传统码头不同的是,自动化码头箱区垂直于岸线分布,且自动化箱区一般采用双ARMG协同作业的方式,其布局如图1所示。ARMG承担了大部分的水平运输任务,ARMG的作业效率直接影响了整个码头的作业效率。所以,对双ARMG的调度优化对于提高整个码头作业效率有重要意义。本文主要根据不可穿越式双ARMG作业范围的不同,设置接力模式和混合模式两种模作业模式,并讨论了这两种作业模式对双ARMG作业效率的影响。
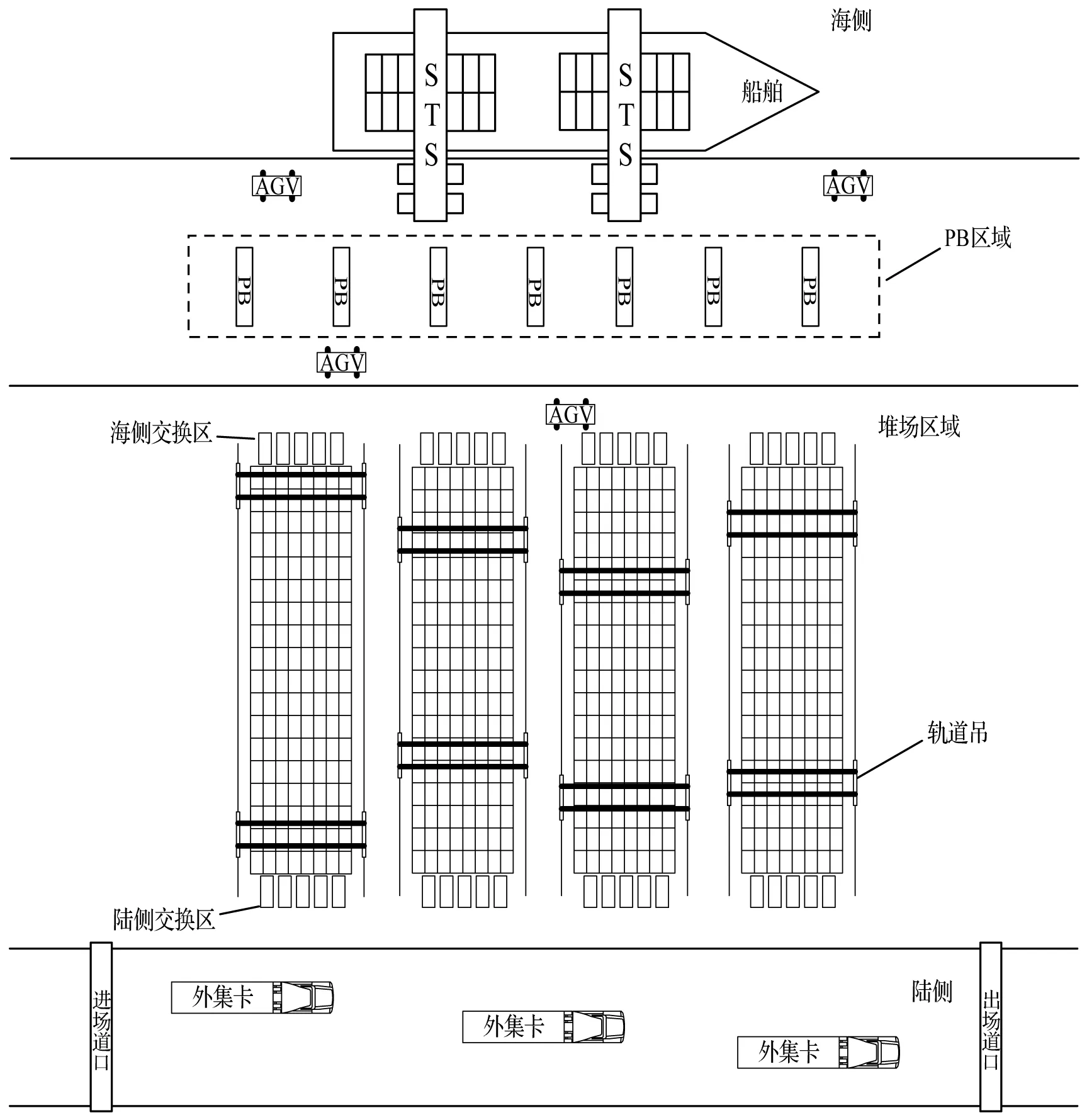
图1 自动化集装箱码头布局图
ARMG是码头作业的效率瓶颈,目前国内外学者对自动化集装箱码头ARMG调度也做了一些研究:
文献[1]提出了基于启发式算法和局部搜索算法的自动化码头双轨道吊的实时调度,研究了不带缓存区的自动化码头堆场的调度问题;文献[2]中,为了得到一个最优结果,作者运用启发式算法,通过讨论是否设置堆场临时储存区,来解决轨道吊调度问题;文献[3]提供了基本的复杂性证明,并引入和测试了有效的启发式解决方案;严伟等[5]在以提供一种新颖的场桥调度策略为目标的情况下,构建了一种基于整数规划的场桥动态调度模型,以达到各时段中剩余的总工作量最小的目标,并采用一种启发式算法:最佳优先搜索算法,来作为求解该模型的算法;林艳艳等[6]考虑场桥实际作业中不可相互跨越与安全距离等特有约束,设计了两阶段启发式算法,通过数据实验对模型与算法的有效性进行了验证;郑红星等[7]考虑了多场桥作业时须有安全距离和不可跨越,以及内外集卡的优先级差异和集卡等待时间有上限等现实约束,对此问题构建了非线性数学规划模型。
部分国内外学者虽对自动化集装箱码头轨道吊进行了相关研究,但是均未考虑接力缓存区对轨道吊作业效率的影响,也没有对轨道吊的作业模式进行讨论研究。本文基于此背景,设置了临时缓存区,并根据轨道吊不同的作业范围,设置了接力模式和混合模式两种作业模式,考虑轨道吊接力问题及轨道吊的安全距离等约束。使用遗传算法,以最小化作业完工时间为目标,计算不同作业模式下的作业效率。最后通过算法对比进一步验证模型和算法的有效性。
1 问题描述
自动化集装箱码头中,每个箱区通常有两台ARMG:一个负责海侧作业,一个负责陆侧作业。两个相同型号ARMG运行在同一轨道上,且不能互相穿越。由于两台ARMG协同作业,因此必须对ARMG的作业范围进行限制,这就导致了箱区中大多数任务需要两台ARMG进行接力完成。其中箱区贝位数从海侧往陆侧增加。
本文根据ARMG作业范围的不同大小,给出接力模式和混合模式两种作业模式,具体如下:
1) 接力模式 海侧ARMG只能在海侧区域(1~27贝)进行作业,陆侧ARMG只能在陆侧区域(24~50贝)进行作业,其中24~27贝为接力任务临时存储区域。若出现陆侧ARMG的目标集装箱在海侧区域,或者海侧ARMG的目标集装箱在陆侧区域,则将该任务分解为主任务和接力任务两个任务进行操作,如图2所示。临时贝位上方为海侧区域,下方为陆侧区域。
2) 混合模式 海侧ARMG和陆侧ARMG可以在一定范围内越过临时存储贝位,进入对方的区域,如图3所示。海侧ARMG允许在1~38贝进行作业(即从海侧到靠近陆侧虚线区域),陆侧ARMG允许在13~50贝进行作业(即从陆侧到靠近海侧虚线区域)。若任务初始位置位于海侧/陆侧ARMG允许进入的箱区区域,则直接作业,如图中的出口装船任务;若任务初始位置位于海侧/陆侧ARMG不允许进入的箱区区域,则依旧使用接力策略。
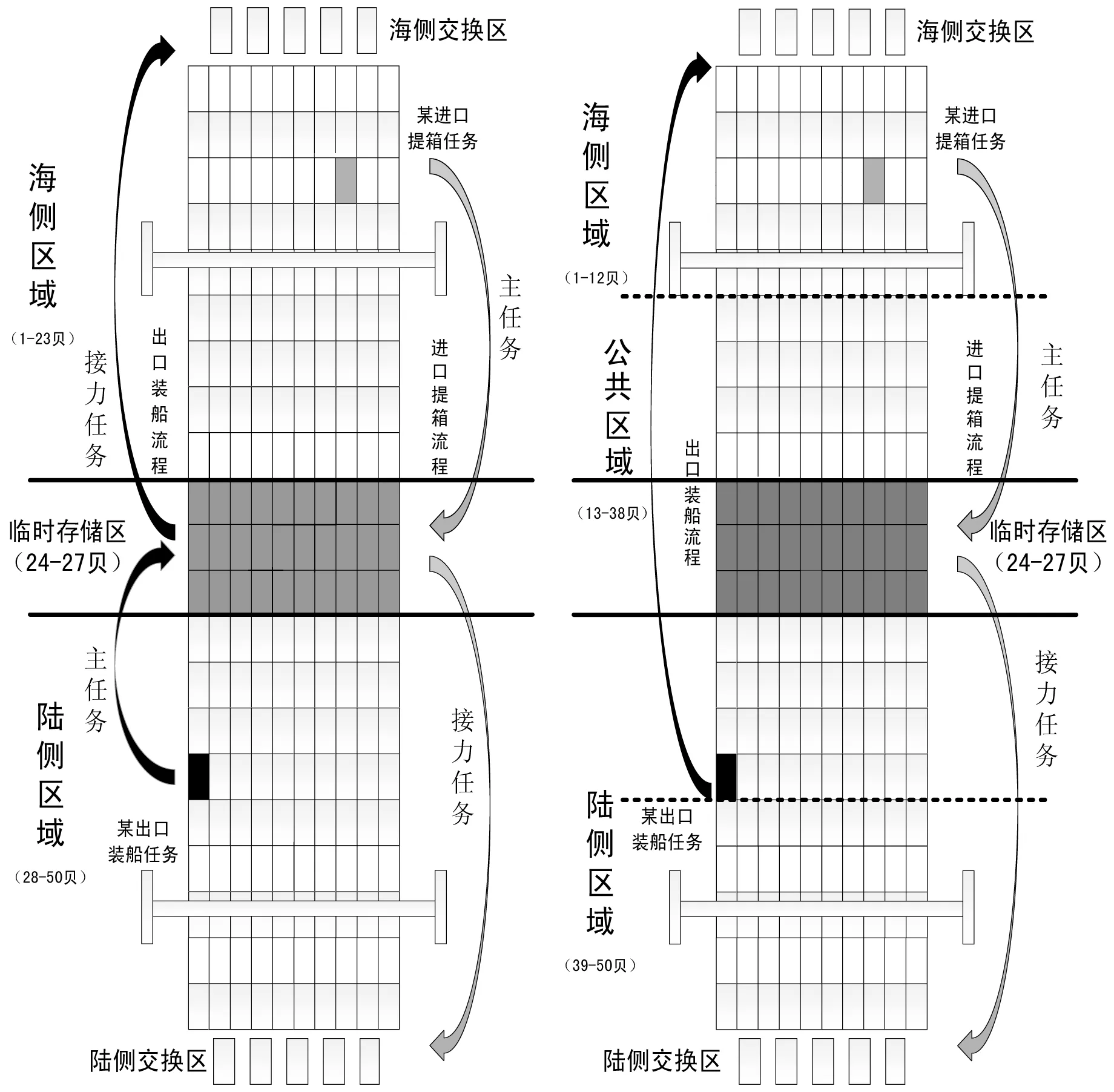
图2 接力模式 图3 混合模式
由于两台ARMG协同作业,存在接力任务的分配问题及ARMG冲突问题。本文根据任务的初始、目标位置来安排ARMG接力作业:若装船集装箱靠近陆侧时,且该位置超过海侧ARMG的作业范围,则须由陆侧ARMG将该集装箱运送至箱区中间的临时缓存区(如图2、图3中间阴影部分),再由海侧ARMG从临时存储区取箱装船;若ARMG调度发生冲突,图4表示两台轨道吊执行任务时发生冲突及其解决办法,由于岸边作业比陆侧作业更重要,赋予海侧ARMG优先作业权,海侧ARMG保持原有的作业线路正常作业,陆侧ARMG不能进入海侧ARMG的工作区域,且要保持一定的安全距离,在区域外原地等待,待海侧ARMG完成作业任务后,陆侧ARMG继续其原来任务。
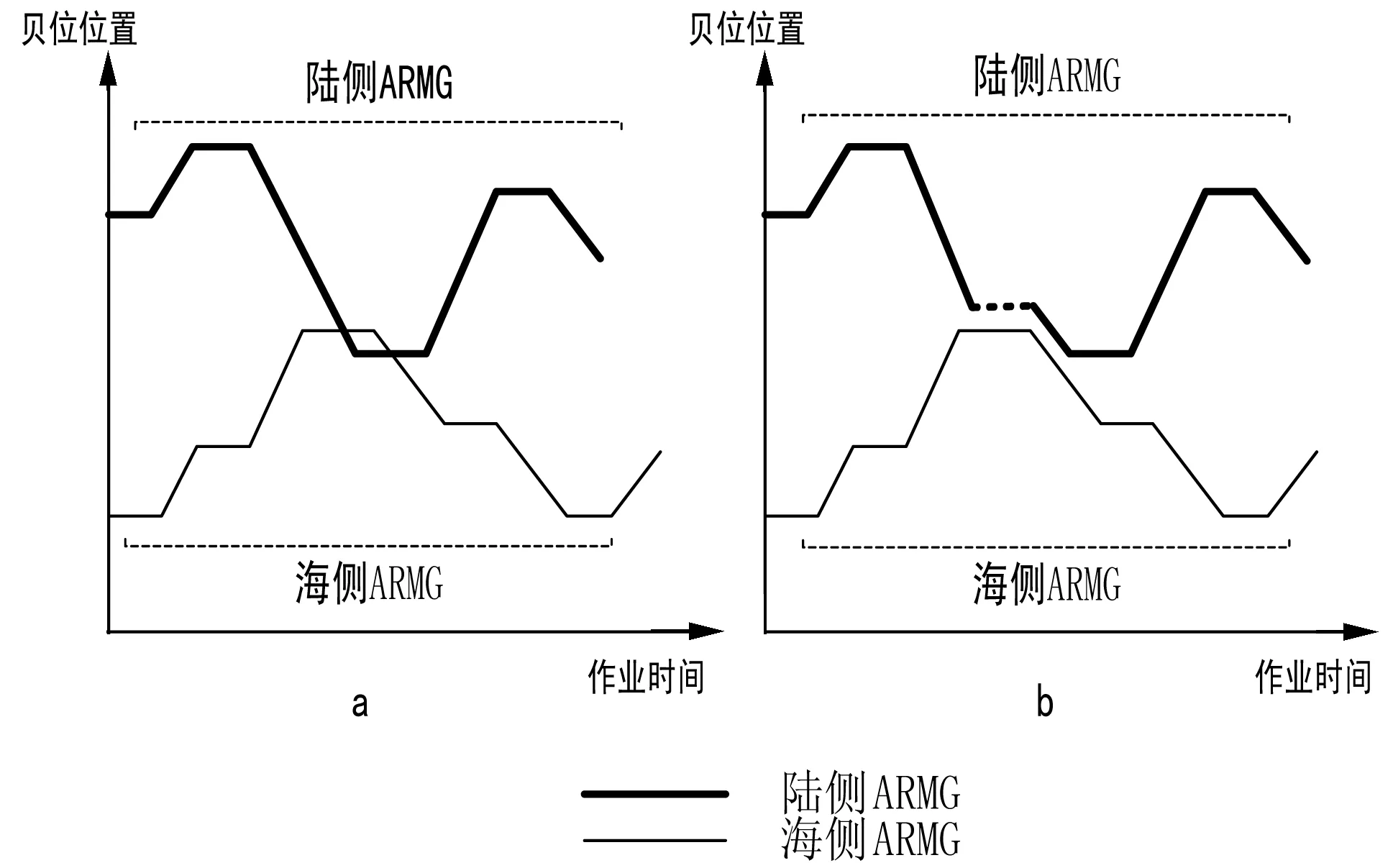
图4 ARMG冲突示意图
2 数学模型
本文考虑ARMG之间的安全距离等约束,建立整数规划模型。为了得到最小化完工时间,本文作出如下假设:(1) 集装箱尺寸统一为20英尺;(2) AMRG装卸时起升速度一致,移动时不考虑加速减速,保持匀速;(3) 堆场两端交互点足够,不存在等待外集卡或AGV的情况;(4) 所有进行作业任务的集装箱均无需翻箱。同时ARMG作业时,必须符合以下要求:(1) ARMG一次只能作业一个集装箱;(2) ARMG移动时不能互相穿越;(3) 不同ARMG不能同时作业相同集装箱。
2.1 参数定义与决策变量
箱区作业相关参数:
n1:主任务的数量;
n2:接力任务的数量;
n:总工作数量n=n1+n2;
M:足够大的数;
Ls:ARMG间的安全距离;
i:表示任意一个提箱或放箱的集装箱操作;
I:表示由放箱操作i和提箱操作n+i组成的一个完整的任务;
Ci:操作i进行作业的目标集装箱;
Li:操作i进行作业时所在的位置;
D1:主作业放箱操作目的地的集合,D1={1,2,…,n1};
D2:接力作业放箱操作至临时箱位的集合,D2={n1+1,n1+2,…,n};
P1:目标箱在初始位置提箱操作的集合,P1={n+1,n+2,…,n+n1},当i∈P1时,Ci=Ci-n;
P2:接力作业中目标箱在临时地点提箱的集合,P2={n+n1+1,n+n1+2,…,2n}当i∈P2时,Ci=Ci-n且Li=Li-n;
Oi:操作i提箱或放箱所用的作业时间;
di:集装箱Ci的主任务的截止时间;
K:ARMG的集合,K={1,2},1为海侧ARMG,2为陆侧ARMG;
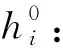
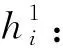
rij:0/1变量,为1表示集装箱Ci堆放在集装箱Cj上,否则为0;
Fi:点i的操作完成时间点;
t:完成所有任务的总时间。
决策变量:
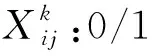
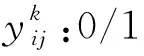
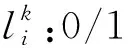
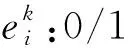
2.2 目标函数及约束条件
目标函数:
Mint
目标函数为最小化作业完成时间。
约束条件:
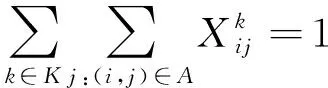
(1)
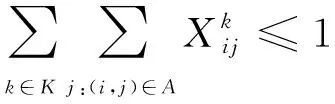
(2)
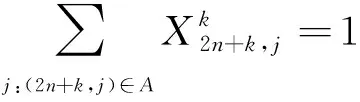
(3)
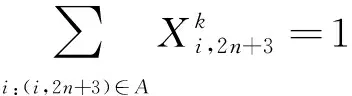
(4)
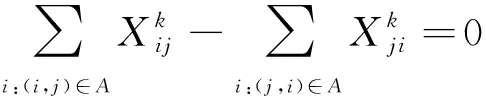
(5)
Fn+i-oi>Fi∀i∈P2
(6)
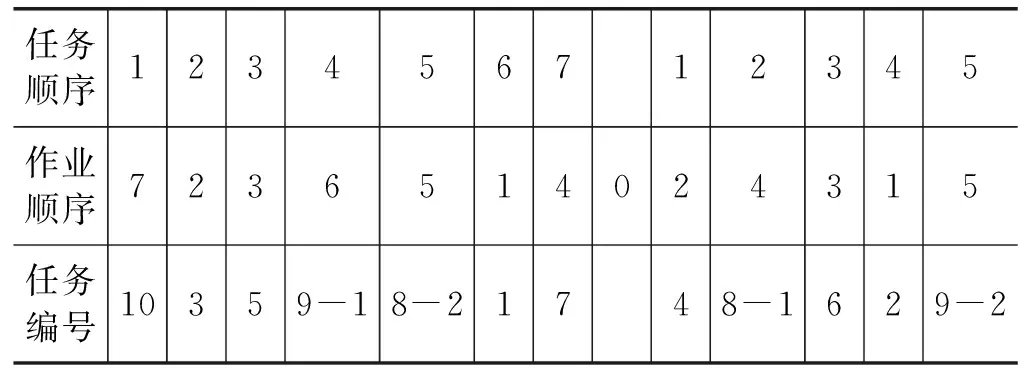
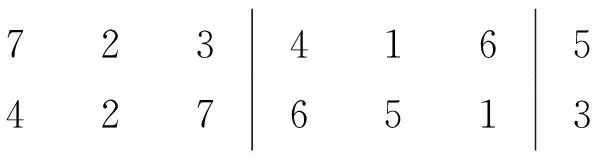
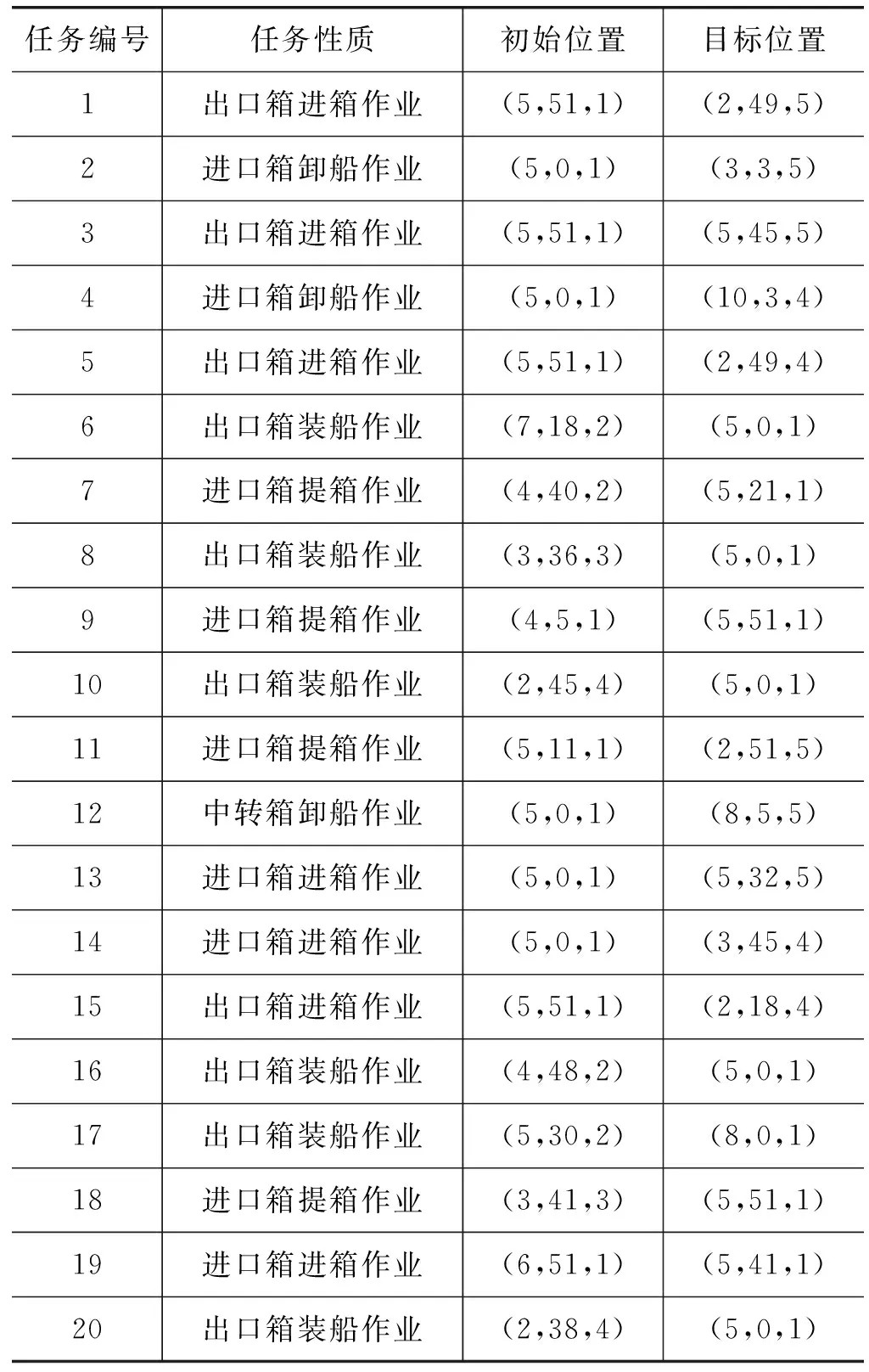
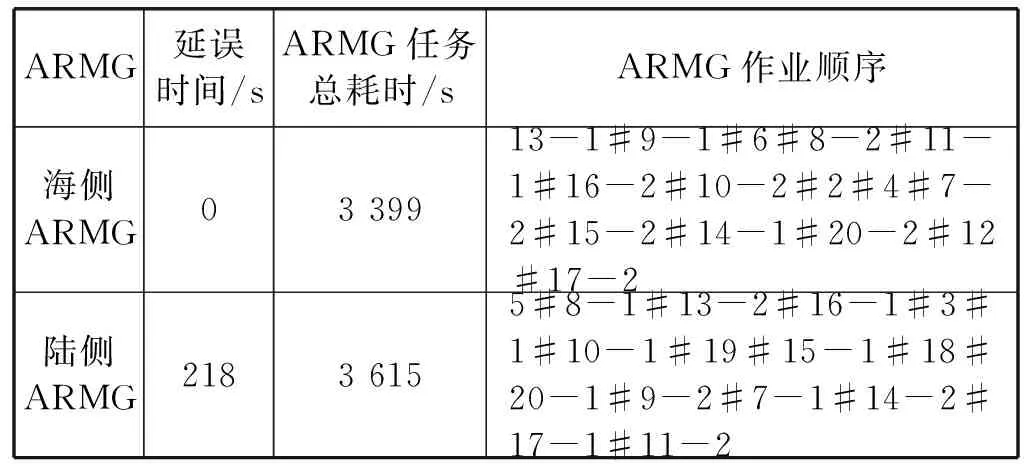
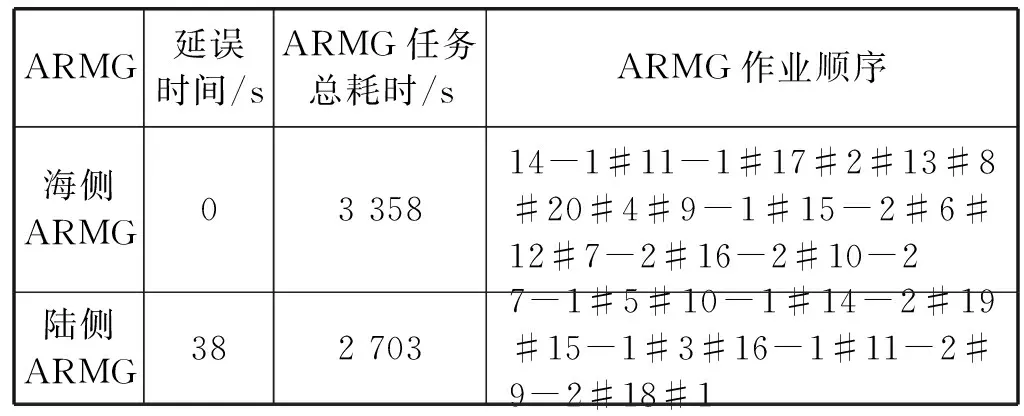
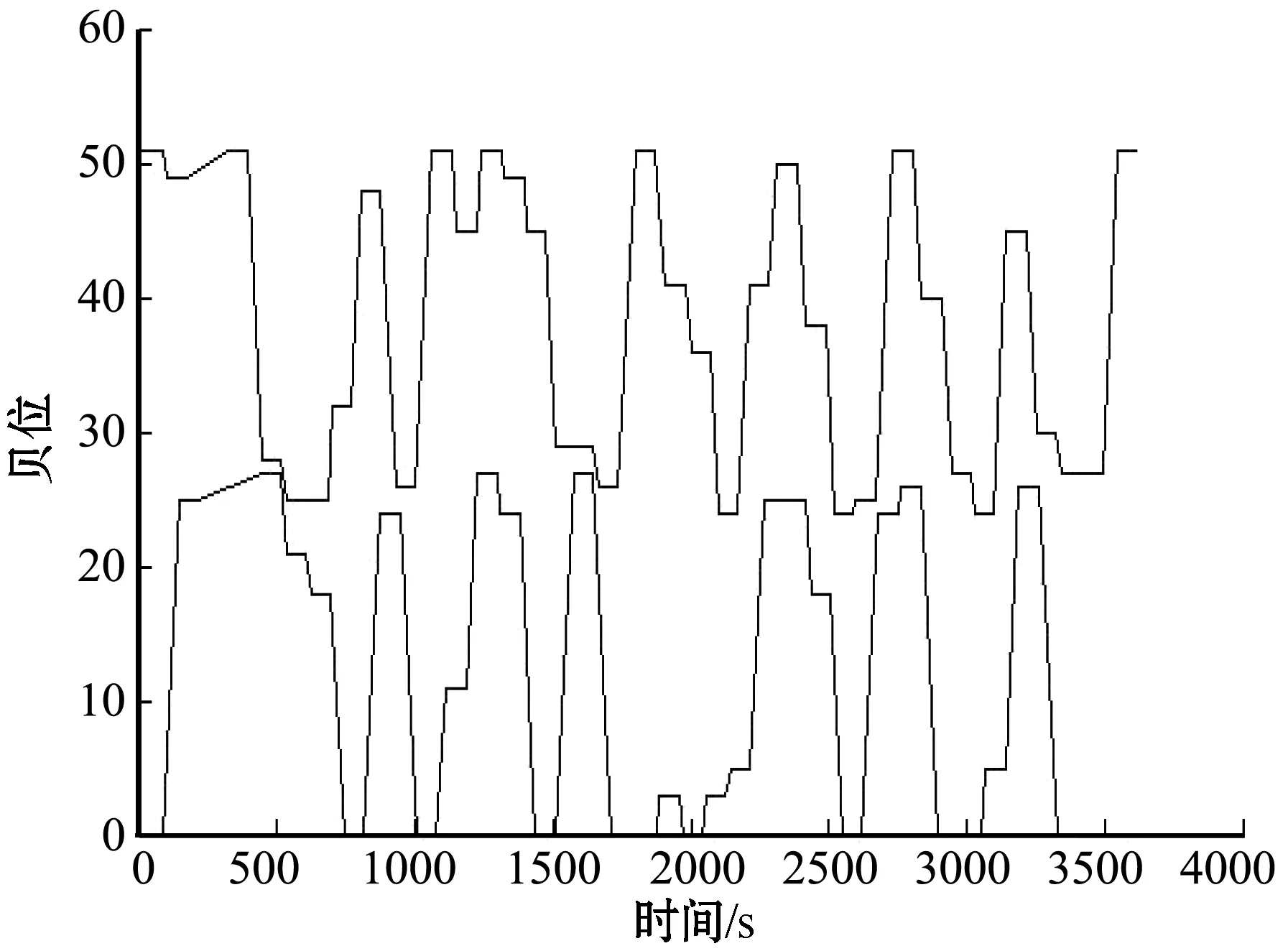
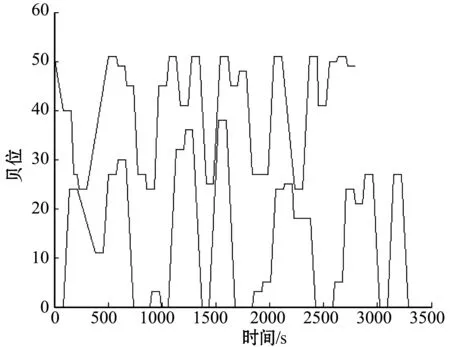
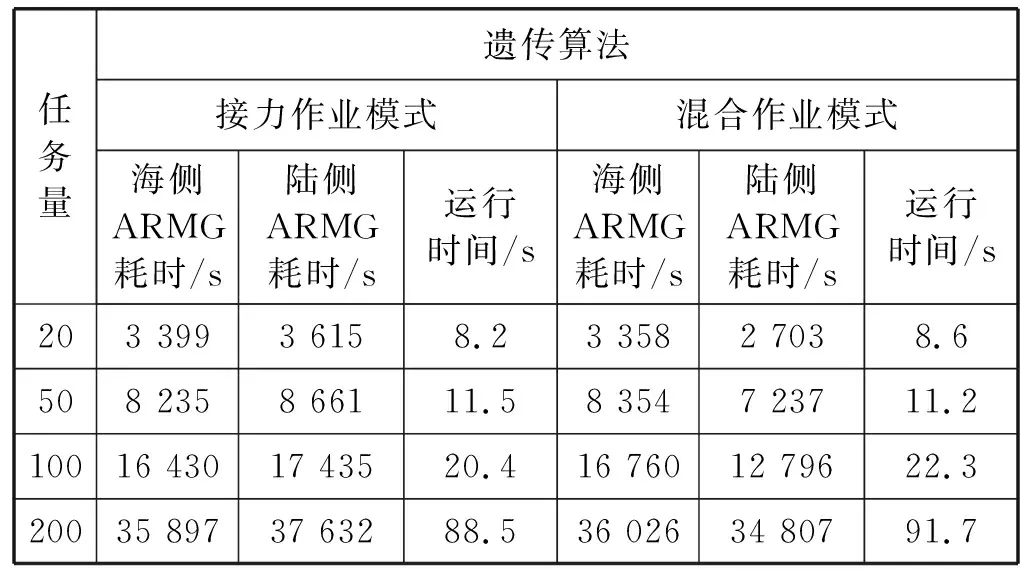
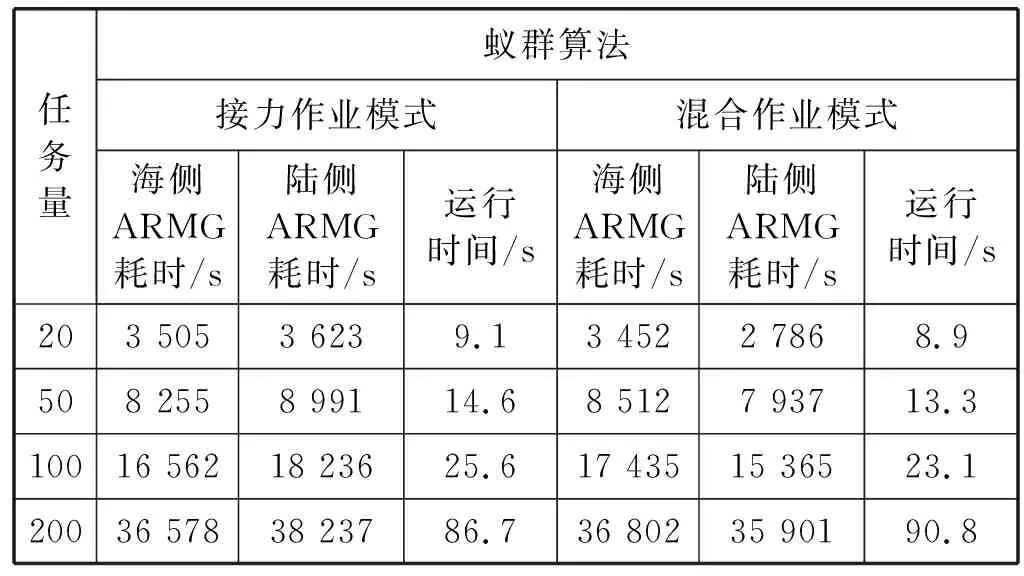
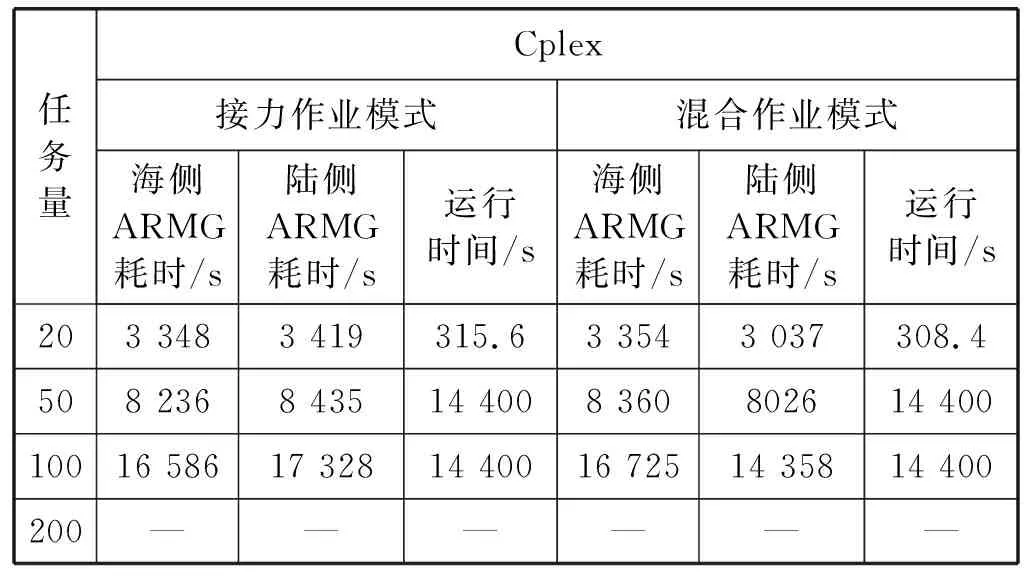
Fi-(Fj-oj) (7) (8) (9) (10) (11) (12) (13) (14) (15) 约束式(1)和式(2)分别表示每一个主作业i∈P1∪D1∪{2n+1,2n+2}必须正好进行一次操作,每个接力作业i∈P2∪D2进行一次操作或没有进行操作。约束式(3)和式(4)确保轨道吊K的路径从点2n+K开始,在点2n+3结束。约束式(5)保证了任务间连线的连续性。约束式(6)描述了临时地点的提箱点应当在这个地点放箱点操作完之后再进行。约束式(7)表示了集装箱堆放中由结构必然导致的先后约束。约束式(8)确保了箱区中总时间由操作时间和ARMG移动时间所组成。约束式(9)确保了靠海侧交接点的任务只能由海侧ARMG完成,而靠陆侧交接点的任务只能由陆侧ARMG完成。约束式(10)表示ARMG之间的安全距离约束。约束式(11)-式(15)表示ARMG的作业状态及其与贝位之间的关系。 本文设计遗传算法进行求解,遗传算法保留每次进化的优势解,逐渐迭代出最优解,适用于作业调度类问题。在算法计算阶段将两台轨道吊单独考虑,即海侧任务全部由海侧轨道吊完成,陆侧任务全部由陆侧轨道吊完成,之后再考虑两台轨道吊协调作业。 假设有10个集装箱任务,其中8、9号任务需要接力完成,假设8-1为陆侧任务,8-2为海侧任务,9-1为海侧任务,9-2为陆侧任务,在接力模式下,海侧ARMG需要完成的任务为1、3、5、7,8-2、9-1、10,陆侧ARMG需要做的任务为2、4、6、8-1、9-2。其采用整数编码,染色体由两部分组成,中间用0分隔。如表1所示,第一部分为海侧ARMG的作业顺序,第二部分为陆侧ARMG的作业顺序。7236514就是海侧的作业任务顺序,表示海侧ARMG需要做的任务为10#3#5#9-1#8-2#1#7;24315为陆侧作业任务顺序,表示陆侧ARMG需要做的任务为4#8-1#6#2#9-2。 表1 染色体编码 在执行交叉操作之前,将整个染色体分解为2个部分,确定交叉操作的父代,两两分组,各种群采用部分映射交叉。假设需要交叉的染色体为7236514024315以及5274163015243,分别拆分为7236514和5274163,及24315和15243。 1) 海侧ARMG的任务数为7个,陆侧ARMG任务数为5个,则产生两个[1,7]区间的随机整数r1、r2,对r1、r2中间的数据进行交叉;同理,再产生两个[1,5]区间的随机整数r3、r4,对r3、r4中间的数据进行交叉。如果r1=4、r2=6、r3=2、r4=4,则海侧染色体交叉: 72365145274163 交叉为: 723416**276513 同理,陆侧交叉: 2431515243 交叉为: *524**431* 2) 交叉后,同一个染色体中,不重复的数字保留,重复的数字(带*位置)采用中间段的对应关系进行映射。结果为: 72341654276513 及 3524154312 以ARMG作业完成20个集装箱存取任务为基本数据。假设一个箱区共有10排、50个贝位、6层,1号贝位为最靠近海侧的贝位,50号贝位为最靠近陆侧的贝位,中间24、25、26、27四个贝位为临时交换区域,第1层为底层箱位,第6层为最高箱位,箱区最左侧排为第1排,箱区最右侧排为第10排。假设ARMG大车(即ARMG门架,垂直于岸方向移动)小车(即吊具)移动速度均为0.5贝位/秒,一个箱位的长度为1贝位,宽度为0.5贝位,层高为0.5贝位,ARMG提取和放下一个集装箱的时间为70 s。假设海侧ARMG初始位置位于(5,0,1),陆侧ARMG初始位置位于(5,51,1),且堆场内集装箱均为20英尺标准箱。遗传算法的设置参考文献[9]:最大迭代数为10 000代,种群数量为60,变异率为0.10,交叉率为0.9,500代内结果无改善则输出最优解。输入数据如表2所示。 表2 作业任务相关数据 本文将采用接力作业和混合作业两种模式分别对ARMG进行作业调度。为不失一般性,堆场临时存储位置随机产生,贝位、排位、层高分别满足U(24,27)、U(1,10)、U(1,6),分别表示贝位满足在(24,27)、排位满足在(1,10)、层高满足在(1,6)上的均匀分布。通过遗传算法计算,得到两种模式下的调度结果如表3、表4所示。 表3 接力作业模式下ARMG调度结果 表4 混合模式下ARMG调度结果 根据表3、表4的调度结果可知,对相同任务数据,在接力作业模式下ARMG最大耗时为3 615 s,混合作业模式下最大耗时为3 358 s,延误时间为ARMG作业冲突时产生的等待时间,混合作业模式下的延误时间也明显小于接力作业模式。由此可以得出本算例运用混合作业模式效率更高。图5、图6分别为两种作业模式下的ARMG作业图,横坐标表示时间,纵坐标表示贝位,可以发现两台ARMG之间也不存在作业冲突问题。 图5 接力模式下ARMG作业调度图 图6 混合模式下ARMG作业调度图 为了进一步分析混合模式的有效性,通过增加集装箱任务数量,运用遗传算法、蚁群算法、Cplex对不同任务数量、不同作业模式下的ARMG进行计算。其具体结果如表5-表7所示。 表5 遗传算法下不同任务量两种作业模式作业时间对比 表6 蚁群算法下不同任务量两种作业模式作业时间对比 表7 Cplex下不同任务量两种作业模式作业时间对比 表5-表7分别为遗传算法、蚁群算法和Cplex的计算结果对比。由表可知,遗传算法在不同任务量下均可得到与Cplex相近的计算结果,而蚁群算法所得到的结果要明显大于Cplex,且遗传算法与蚁群算法在计算时间上相差不大。当任务量大于等于50时,Cplex运行时间较长,因此在本算例中,设置14 400 s作为Cplex的最大运算时间。随着任务量的增加,Cplex在任务量为200时,无法在可接受范围内求解出最优解,且遗传算法得到的解也越来越优于蚁群算法。因此通过遗传算法、蚁群算法、Cplex的对比结果,可以将遗传算法得到的结果接受作为最优解。 本文以自动化集装箱码头ARMG协调调度为主要研究内容,针对临时缓存区大小对ARMG作业效率的影响,考虑ARMG冲突及安全距离等问题,以最小化任务完工时间为目标,根据缓存区大小设置了两种不同的作业模式,并运用遗传算法进行求解,得到混合模式比接力模式效率更高。再分别通过遗传算法、蚁群算法、Cplex计算不同任务量下的完工时间,并通过实验结果的对比,验证了遗传算法计算出的结果的有效性。虽然本文得到了较为理想的结果,但是也存在不足,未考虑实际集装箱任务的随机性,以及ARMG与陆侧集卡、海侧AGV的协调问题等,这些都将增加ARMG的调度难度,但是也更符合码头实际作业,因此会在以后的研究中逐一解决。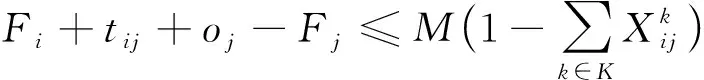
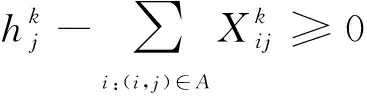
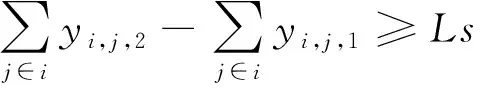
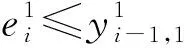
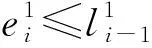
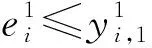

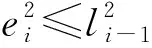
3 算法设计
3.1 编码和解码
3.2 交 叉


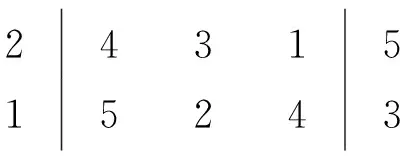

4 算例分析
4.1 参数设置及输入数据
4.2 两种模式下的结果分析
5 结 语

