基于亚线性MG替换策略-网络流的动态车流量检测方式

沈智勇 苏 翀* 沈智威 孙厚权 周 扬

1(江苏科技大学 江苏 张家港 215600)2(苏州大学 江苏 苏州 215000)

0 引 言

随着时代的发展，交通情况越发不确定，出行的安全度和舒适度逐渐受到重视。随着私家车日益增加，人们出行更为便捷的同时，所造成的交通拥堵往往带来诸多不便。用户往往只想知道自己出行中起点到终点之间的道路情况，而对其他路上的道路情况不感兴趣。

已有的交通路况检测大多基于图像处理与识别，这种方法不但耗资巨大，对于图片信息的储存数据量也是一个问题，若只在少数路口安置摄像头进行分析车流量，图像分析大多适应于相对静态的情况或者车速较慢的情况，对于整条道路的动态车流量精度不能有明确保证。对于动态车流量的检测，本文提出了一种基于亚线性MG算法的替换策略。

本文的主要贡献如下：

(1) 提出一种基于亚线性的替换策略；

(2) 提出的亚线性算法能较好地应用于路况检测；

(3) 选择出一种高效的能与替换策略相结合的基数桶数据结构，保证了空间的亚线性。

实验结果表明，该算法对于车流量的检测与计算具有一定的可行性，相对于基于图像处理的检测方式降低了数据的纬度，提高了计算的速度，同时保护了个人的隐私。对于基于红外方式的检测方式本文提出的算法能大大提高数据的可信度，提高结果的正确性。

1 相关工作

1.1 ViBe算法检测路况

ViBe算法利用视觉背景提取改进车流量估计，对静止目标有非常良好的计算效果。ViBe算法能很好地抑制假影现象，将检测器安装至道路交通口，利用红灯效应可对车流量进行准确检测，提高了车形清晰度，提高了检测的正确性[4,8]。但ViBe算法本身仍存在运动目标不完整等问题。

1.2 红外检测路况

当前普通的基于红外的道路检测系统，利用脉冲进行简单计数，由采集模块、交通灯控制模块和模拟控制中心。基本上完成了车流量检测的功能，但并未对其中收获的数据进行简化和计算，难以保证数据的准确性，失去了数据的意义。

2 亚线性MG替换策略-网络流检测方式

基于亚线性MG替换策略-网络流的动态车流量检测方式通过利用自制道路检测器安置红外对管，利用每个数据收集器收集的车辆通行数目。对道路情况进行算法分析与研究[2-4,6,10-11]。

本算法先求解出单条路径的动态车流量，将此条路径的车流量抽象成图中的一条边，根据大数定理构建图，根据段流量求解出最大流，根据相关知识得出交通状况。

算法总体设计流程如图1所示。

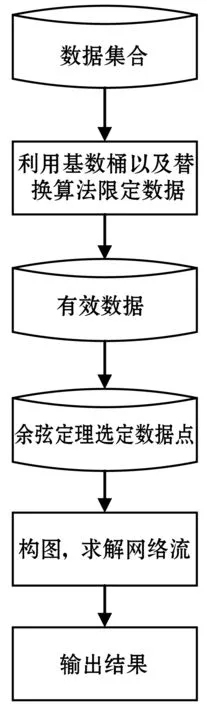
图1 算法总体设计流程

3 亚线性替换算法

3.1 基数桶

道路上存放N个检测器，分别检测到的数据将依次存放至基数桶中。根据Zipf定理，可以确定基数桶结构[1]是有效的。本文根据Zipf定理确定基数桶中的容量是全部数据值的10%。

基数是集合论中的一个概念，将相似的数据放入一个基数桶，并保证基数桶中各集合各自保证非递减有序。

建立9个的基数桶，桶状结构样例如图2所示。

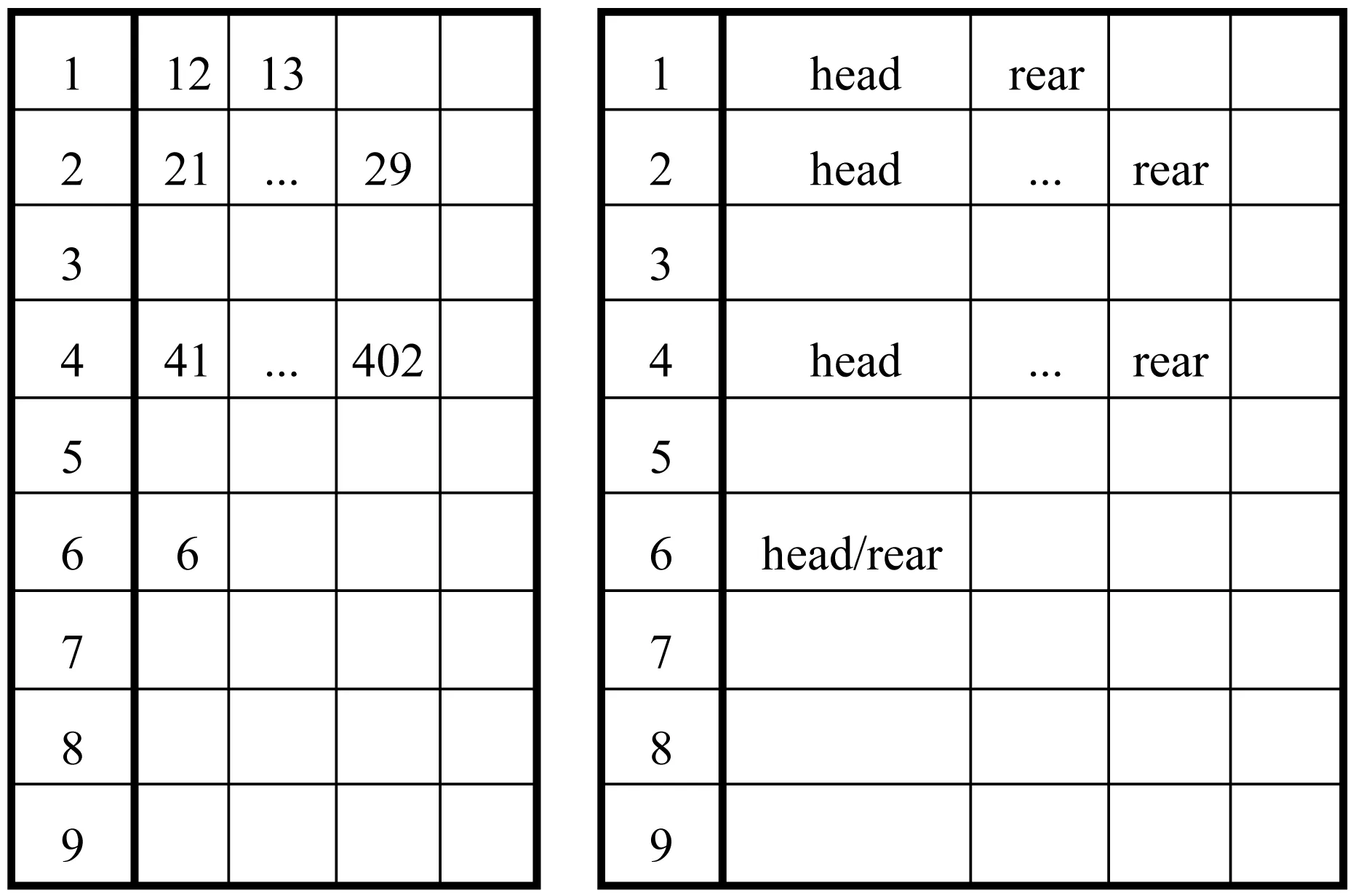
图2 基数桶数据结构图

数据i进入基数桶中只需进入该对应集合，数据i进入基数桶时对数据的最高位进行划分，如：12最高位是1，则进入1号基数桶，29的最高位是2，则进入2号基数桶，其优势在于与其他数据保持独立性。当有新的数据进入基数桶，如41进入基数桶，只需考虑基数4中集合所存在的元素，由于非递减有序特性，利用插入排序对数据进行增加或者更新。

同时设置队头游标和队尾游标分别指向各个集合的队头和队尾。随机算法替换数据时只需比较每个基数集合中的队头游标与队尾游标中所指向的数据。

同时基数桶中的元素可利用块状链表[13]的形式对数据进行初始化、更新和插入，此时数据运算时的时间复杂度可大大降低。

当进行数据处理是空间复杂度显然只与基数桶容量有关，是空间亚线性的。

3.2 随机化与改进MG替换算法

本文利用红外检测器检测道路流动车流量，并做出如下假设：

(1) 道路是单向的。

(2) 道路没有交叉口。

根据上述假设可以得出：在单向无交叉口的一段连续道路上的检测器在单位时间内测定的数据值大部分是相同的或是相似连续的(车流量并不能突变)。图3表示在以上假设下检测器检测结果模型图。

图3 检测器检测结果模型图

当a测出值为5，那么b测出的值应与a的检测值相同或相差车道数m的倍数，且a、b检测值差值不大。

根据以上假设推论：如果道路拥有交叉口，那在两条交叉口之间的检测器中的数据大部分是相同的。

利用Zipf定律可以得到一个大致的模型，90%的道路情况数据占所有道路情况数据值的10%(10%的数据值分布在不同的路口，有岔路等地)，我们可以称这90%的数据是有效数据，剩下10%的数据是无效数据。但这90%的数据中不同的数字只占全部数据的10%，根据以上论述可以得出随机化的合理性和有效性，亚线性替换算法描述如下：

Input：检测器检测到各个数值in[]；

Output：替换算法返回结果，基数桶中的有效数据out[][]；

1 While in[]!=empty:

2 i=0;

3 s←取[0,9]之间的任意一个随机数；

4 i++;

5 cardinal←in[i*9+s]所对应的基数

6 Size←基数桶容量

7 If Size !=full:

8 If s∉out[][];

9 s放入基数桶;

10 Out[ cardinal][].count++;

11 End If

12 End If

13 If Size==full:

14 If s∈out[][]:

15 s.Count++;

16 Else

17 For each out[ cardinal][]:

18 Out[ cardinal][].count--;

19 If out[ cardinal][].count==0

20 Flag=1;

21 移出基数桶;

22 End If

23 If flag==1

24 s放入基数桶

25 End If

26 End If

27 End While

算法有效性分析如下:

(1) 对于上述算法，由于关键在于随机选取的间隔d应对于具体问题具体分析，由于随机化，算法的时间复杂度严格小于数据量n，计算复杂度只与基数桶中的数量有关，故替换算法是时间亚线性的。

(2) Misra Gries算法步骤表明：在数据流中到达的项i进行如下的步骤：如果项i在数组T中，则其对应的计数器++c；如果项i不在数组T中，且数组T中的元素个数小于k-1，将项i加入数组T，并为其分配计数器ci=1；其他情况，将数组T中所有元素的计数器减1，此时如果数组T中存在元素的计数器值为0，则从数组T移除这个元素。MG算法保证了亚线性，本文将计数器的计算由全部数据缩小至基数桶的各个基数所对应的基数项的计数器计算此数，基数桶结构也将计算复杂度大大降低，满足亚线性。

(3) 替换算法替换出的是最不频繁出现的数字，也就是说当替换次数越多，出现无效数据的概率就越低。因为根据Zipf定律，有效的数据占了90%，无效的数字只有10%，这些数据肯定是最不频繁的数字，那优先替换的是这些数字，故替换算法具有有效性。

(4) 关于随机间隔d的选取：根据zipf定理，最少有90%的数据是有效数据，这些数据的数据值占所有数据值的10%(数据与数据值的概念如图3所示，其他情况的比例可由实验大致得出)，那么剩下10%的数据是无效数据，这些数据的数据值占所有数据值的90%，这90%的数据值基本上是与10%的无效数据一一对应。即若某数据值只出现一到两次，那么这个数据值很有可能是无效数据，否则多次出现的数据值便不能称之为无效数据。而对于有效数据，多个有效数据对应一个数据值，难以定量计算，故假设数据量为n，数据值为m，有如下等式：

0.1n=0.9m

(1)

则：

n=9m

(2)

推论：每9个数据中拥有1个数据值，根据上述证明，数据值一般为集中存在于交叉口与交叉口之间，故可确定连续的间隔，并确定随机间隔为9。

对于上述选择的间隔d=9,选取有效数据的概率为：

即当你用随机选取数据时，选择有效数据的概率有90%。当数据进行替换时有效性将大大高于90%。

4 多路径问题

4.1 圆形限定数据点

上文介绍了对于单路径数据的数据，以下给出多路径的数据处理，根据起点至终点选择哪部分数据进行计算。本文利用余弦定理筛选数据，具体筛选过程如下：只选取在源点与终点间圆形区域内的数据，将源点与终点连线构成直径，当输入数据时只需判断三条边长度平方之间的关系，当a2+b2-c2<0，那么该点在圆形内，当a2+b2-c2>0，那么该点不在圆形内，如图4所示。之所以利用圆进行数据选择，是根据等周不等式在相同周长情况下，圆形面积最大，选择数据更多，效果更好。

图4 圆角度图

4.2 大数定理与最大流

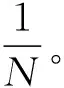
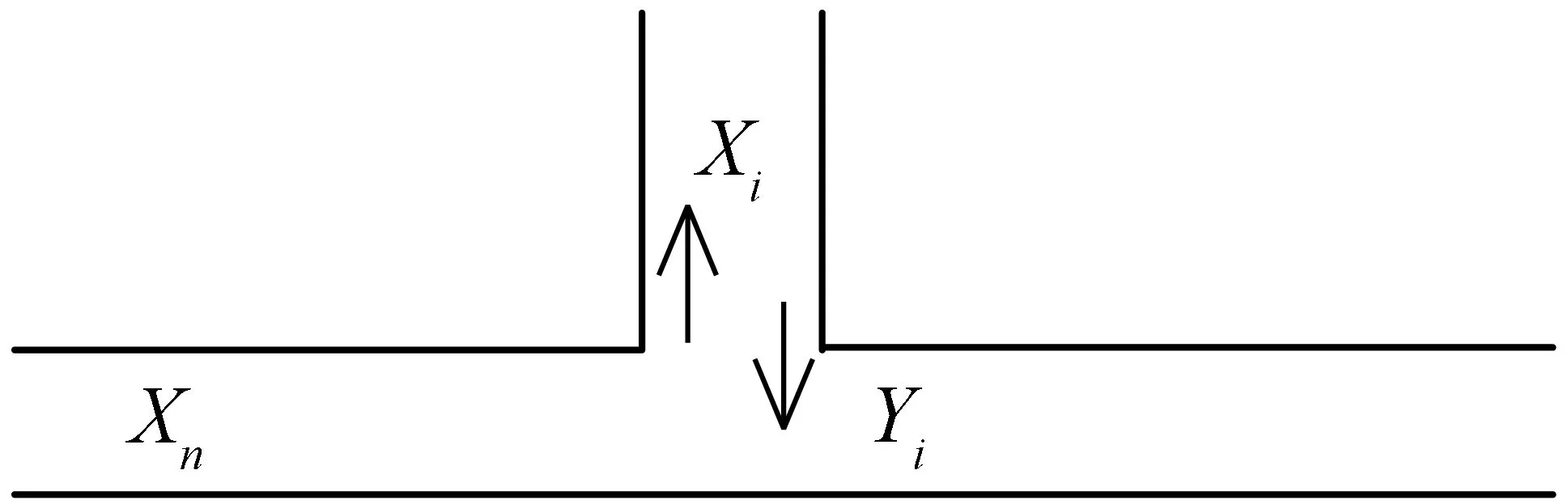
图5 岔路模型图

其公式为：

(3)

又可根据总流量与出入流量xi、yi的关系得出：

(4)

证得：

故有：

(5)

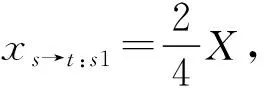
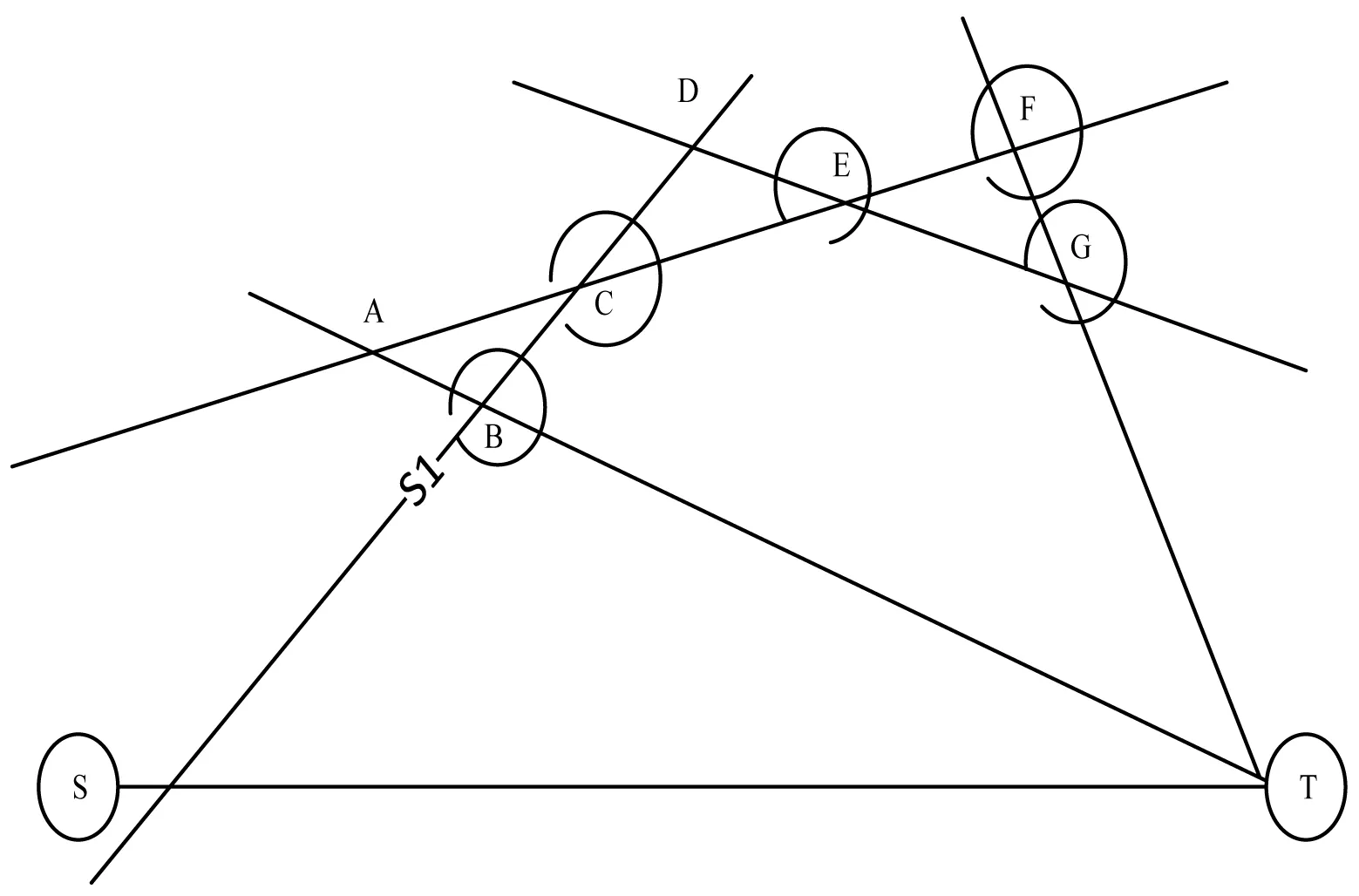
图6 多道路径模拟图

输入起点与终点，利用余弦定理选择数据，分别求出各个节点之间的段流量，求出该图的最大流[5]。

5 实验与讨论

5.1 实验设置

实验将所提出的的MG算法与纯红外检测算法分别在计算复杂度、空间复杂度两个方面做比较。数据量分别选择容易计算的100的倍数进行计算，分别为100、500、1 000、5 000、10 000。

实验平台是64位Windows10操作系统笔记本计算机，内存4 GB，CPU 2.5 GHz，实验语言C++。

本文使用http://www.cs.unibo.it/projects/bolognaringway/所提供的数据，对数据进行整理，所需数据样表如表1所示。

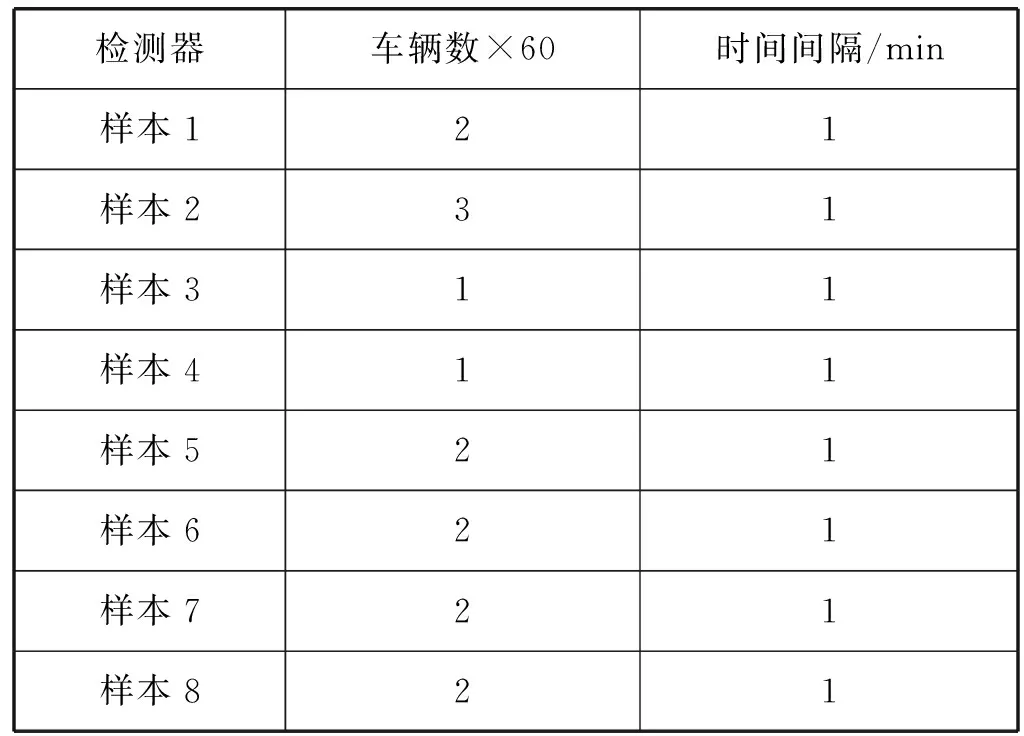
表1 实验数据样表

5.2 实验结果

对于空间复杂度，纯红外复杂度为数据集数据个数N，对于本文空间复杂度为基数桶容量V。

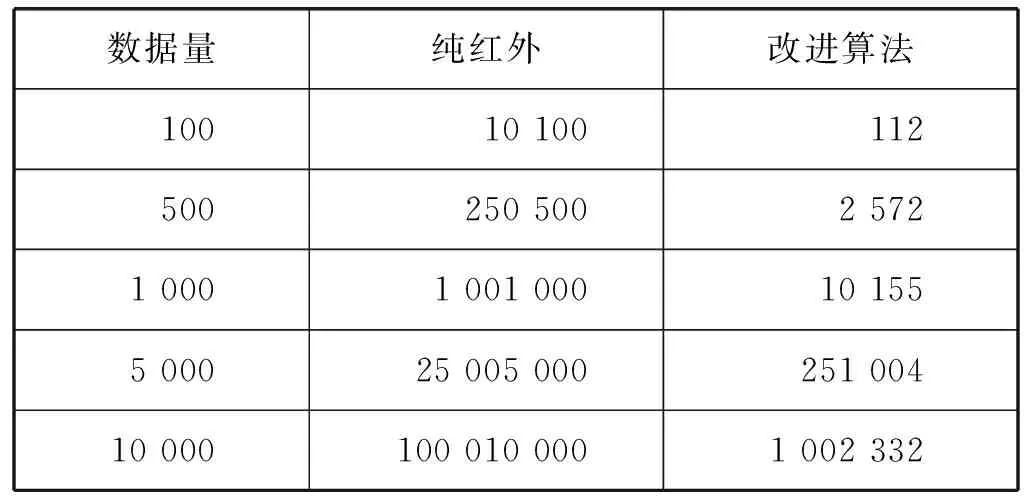
表2 计算量对比

根据表2可知，未优化的检测方式与本文方式从计算复杂度上有较大差距。

5.3 实验结果与分析

当数据流中的数据进行判断的时候可以说它们服从二项分布(有效数据和远离数据)。随机变量x～B(n,p)，对于任意的实数x，当数据量很大时[10]，有：

(6)

即，在大数情况下二项分布近似服从泊松分布，分布样图如图7所示。

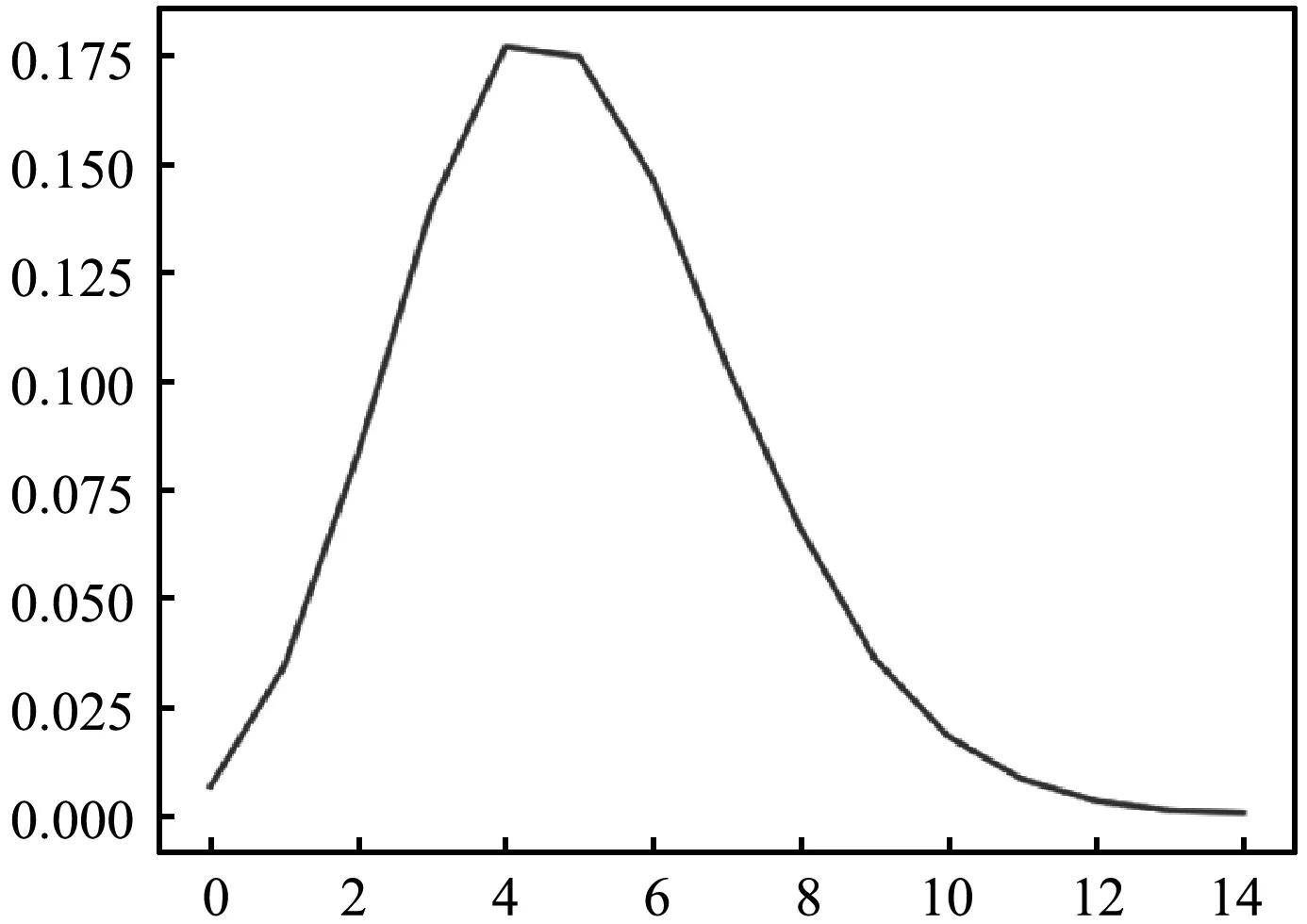
图7 分布样图

在泊松分布的最左端是基数桶中基数为[1,2,3,…,9]中的head中最小游标指向的数，最右端是基数桶中基数为[1,2,3,…,9]中的rear中最大游标指向的数。

本文利用基数桶中的数据计算泊松分布的估计值，利用这个估计值代表这条路径的动态流量，X(1),X(2),…,X(N)为服从泊松分布P(λ)的独立样本。则：

Ex(k)=λ,k=1,2,3,…,N

(7)

(8)

道路拥堵参数JAM，即能导致道路拥挤的最大的动态流量，由城市道路情况设定。显然，在一定程度内最大流动车流量max_flow越大，道路情况越好，但当max_flow达到某个限制，道路车辆陡增会导致道路拥挤。当max_flow

图8 变化循环图

由此可得出以下实验结论：只需比较上一时间段的数据即可判断道路情况，若流量陡降则发生拥堵；若与上文流量保持均衡，流量平稳则不拥堵；若流量均匀下降或者均匀上升道路,情况稳定不发生拥堵；若流量陡增则道路动态车流量大，则也没有发生拥堵。

本文利用基数桶中所得的期望作为数据点计算标准差，利用标准差表示车流量突变情况。

(9)

根据数据的处理，可得如下结论：

(1) 在数据范围很小的情况下，亦或是在极端情况下，即当线路是一条直线时，最大流接近于红外接收信息的计数均值，计算速率快。

(2) 当数据范围很大的情况下，本文数据结构保证了数据的可靠性，使用的算法在时间亚线性计算速率相比于普通的替换策略算法有明显优势。

6 结 语

本文提出的基于亚线性MG-网络流算法应用于检测道路路况，对检测高速动态车辆有比较好的效果。实验证明，该算法能够很好地达到检测目的，并且对于数据，选择了计算度最低的点数据，能够很好地降低数据处理的难度和复杂度。但不足之处在于：当交通路线过于复杂，其桶容量不足会导致系统误差，因此算法在道路错综复杂度过高的情况下，精度不高。