关注三角知识的解题功能

黄旭明

(福建省福安市第三中学 355002)

在三角函数的学习中，常常把学习的重心放在三角函数的图象性质与三角公式的变形技巧上，而忽略了三角知识的应用价值.实际上，如果在解题中能恰当地引入三角知识，可化繁为简，化难为易，优化解题，突显三角知识的解题功能.本文分类举例介绍三角知识在诸多问题中的广泛应用.

一、求解最值问题

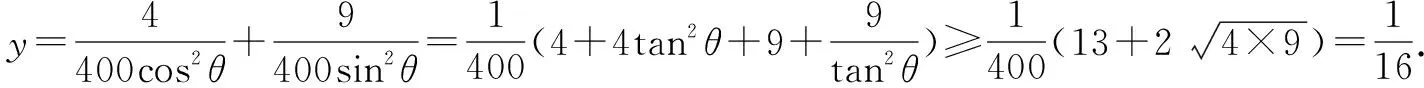
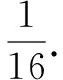
二、求解取值范围问题

例2 若2x2-2xy+y2=1,则x+2y的取值范围是( ).

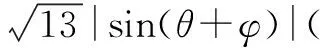
三、求解不等式问题

例3 已知|x|≤1,求证(1-x)n+(1+x)n≤2n(n∈N*).

证明由条件|x|≤1,可设x=cosx(0≤α≤π),则

四、求解数列问题

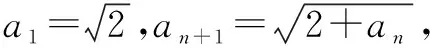
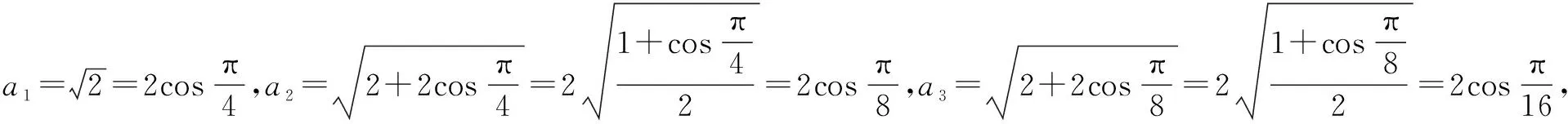
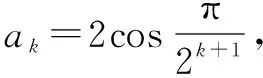
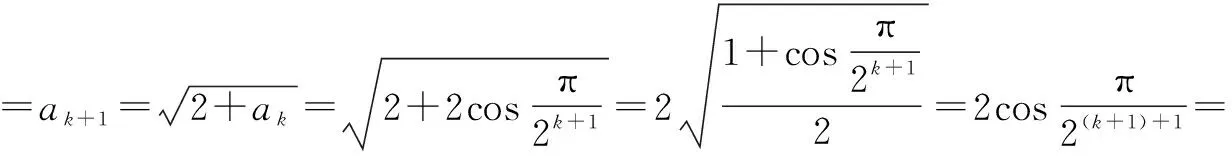
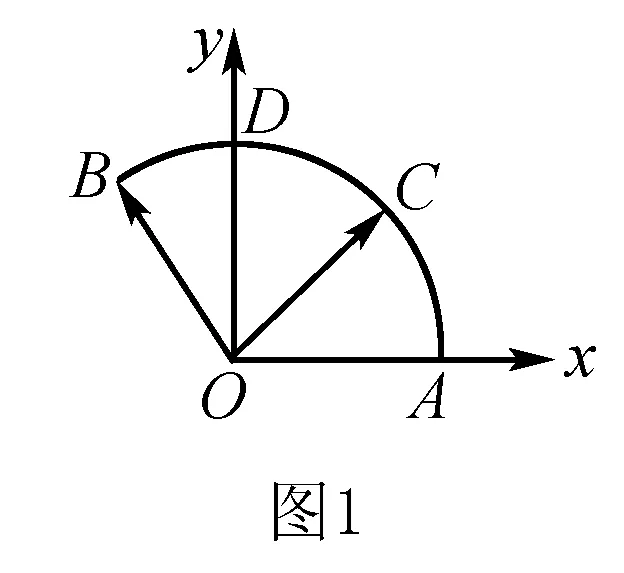
五、求解向量问题

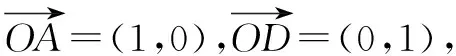
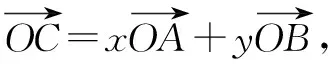
六、求解平面几何问题

例6 如图2，是三个并排的相同正方形，求角α+β的大小.

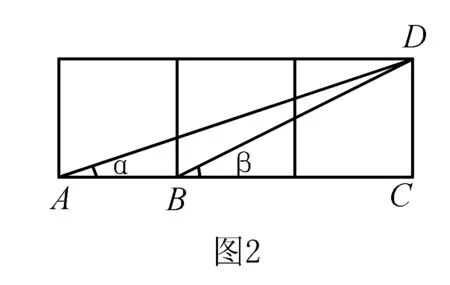
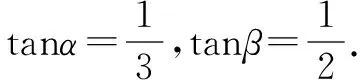
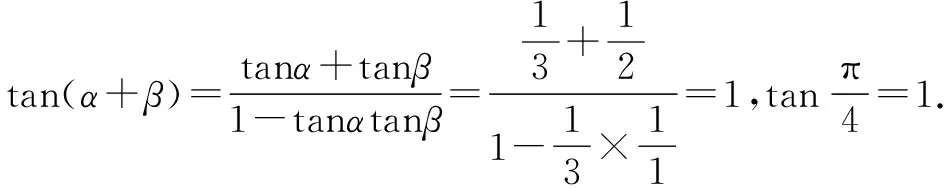
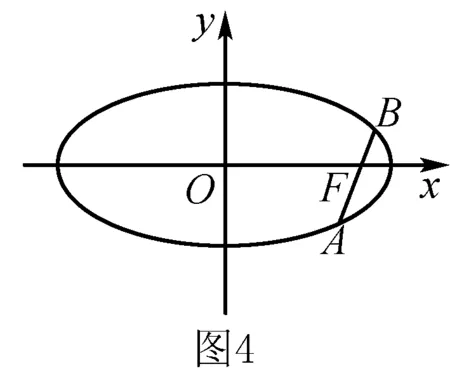
七、求解解析几何问题

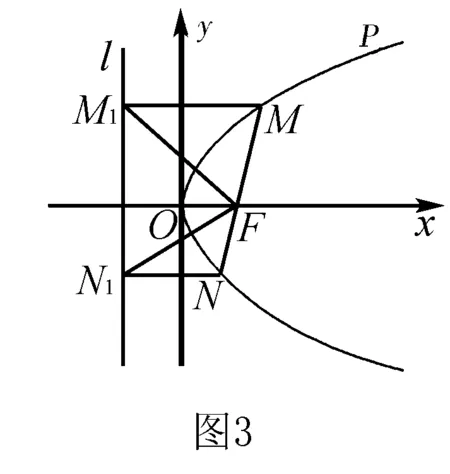
例7 如图3，过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点，自M、N向准线l作垂线，垂足分别为M1、N2.

解(1)记l与x轴的交点为F1.由抛物线定义知FM=MM1,FN=NN1,又MM1∥FF1∥NN1,故∠MFM1=∠MM1F=∠M1FF1,∠NFN1=∠NN1F=∠N1FF1.

所以∠M1FF1+∠N1FF1=∠MFM1+∠NFN1,得∠MFN1=90°，所以FM1⊥FN1.

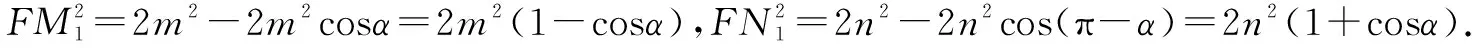
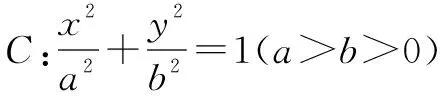
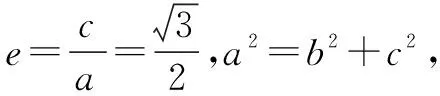
从以上诸例可以看到，三角的知识和方法可运用到各种类型的题目中，而且可以化隐为显，化难为易，从而应用熟知的三角方法顺利实现解题.实际上，各章节的数学知识都有广泛的应用，注意挖掘出各种数学知识方法的工具作用，对培养数学意识，增强解题能力，提升数学素养，具有重要意义.