基于改进自适应正交匹配追踪算法的手势识别

李 贝 孙 瑛,2 李公法,2,3 蒋国璋,2,5 孔建益,2 江 都,4 陈迪斯,3

1.武汉科技大学冶金装备及其控制教育部重点实验室，武汉，430081 2.武汉科技大学生物机械手与智能测控研究中心，武汉，430081 3.武汉科技大学精密制造研究院，武汉，430081 4.武汉科技大学机械传动与制造工程湖北省重点实验室，武汉，430081 5.武汉科技大学3D打印与智能制造工程研究所，武汉，430081

0 引言

众所周知，手势识别作为一种自然的交互方式，被广泛用于人工智能和模式识别领域。基于视觉的手势识别主要采用摄像头捕捉手势图像，通过图像处理和相关算法识别手势动作，涉及到的技术包括手势检测分割、特征提取和分类识别等。这些技术近年来虽然有很大发展，但由于视觉传感器采集手势进行识别时，常常会遇到背景环境复杂、分类算法性能不高等问题，因此对于精确的手势识别研究仍存在一定的挑战［1⁃2］。近年来，稀疏表示理论的提出和发展为模式识别提供了新方法［3⁃4］，表现出较大的发展潜力和广阔的应用前景。WRIGHT等［5］提出稀疏的表示分类（sparse representation⁃based classification，SRC）框架将训练样本用于构建冗余字典［6］，通过稀疏求解算法［7⁃8］，测试样本可以表示为训练样本的稀疏线性组合，最后根据最小残差分类［9］，成功解决了分类算法性能不高的问题。

SRC方法提出后，稀疏表示理论逐渐得到研究人员的重视［10］，研究者在稀疏求解算法方面提出了各种方法。常用的稀疏求解算法主要有近似求解最小化l0范数问题的贪婪算法。贪婪算法通过迭代选取合适原子，易于实现，常用的正交匹配追踪（orthogonal matching pursuit，OMP）算法［11］每次迭代时只选择一个原子，迭代次数多、效率低，而且需设定稀疏度。针对OMP算法存在的问题，出现了许多改进算法，如为了在每次迭代时选择多个原子，提出基于正则化的ROMP（regularized OMP）算法［12］、基于原子选择阈值的SWOMP（stagewise weak OMP）算法［13］、基于回溯思想的SP（subspace pursuit）算法，SP算法的优势在于降低了计算复杂度，但大部分算法都依赖于稀疏度［14］。SAMP（sparsity adaptive matching pursuit）算法沿用了SP算法的回溯思想，而且可以利用固定步长逐渐逼近稀疏度，其优势在于利用步长逼近的方法进行分阶段迭代，每个阶段增加固定步长直到满足要求，其缺点是固定步长的选择会对算法性能有较大的影响［15］。

本文从稀疏表示分类算法原理入手，针对现有贪婪算法在稀疏度估计上的优势和增加固定步长的不足，引入稀疏度估计方法和变步长的思想，提出改进的自适应正交匹配追踪（modified adap⁃tive orthogonal matching pursuit，MAOMP）算法，并在手势库上进行验证，实验结果表明所提出算法性能优于其他算法性能，有效提高了算法的精度和效率。

1 稀疏表示分类算法

稀疏表示分类（SRC）的基本思想是将训练样本构成冗余字典，则测试样本可以由该字典元素的稀疏线性组合表示，然后采用稀疏重构算法求解稀疏系数。SRC算法主要涉及两个方面，即冗余字典的构造和稀疏系数的求解。

1.1 测试样本作为训练样本的线性表示

给定包含C类手势的样本集（总样本数为n），假设第j（j=1，2，…，C）类包含nj个手势样本且样本足够多，该类的第i个手势样本可以用列向量aj,i∈Rm×1表示，将该类手势样本组成列向量矩阵Aj=[aj,1aj,2… aj,nj]∈Rm×nj，m是该矩阵的维数。理论上属于第j类的某个测试样本y∈Rm分布在该类样本集所形成的一个线性子空间中，即y可由Aj线性表示：

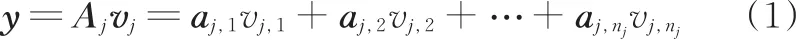
式中，vj=(vj,1,vj,2…,vj,nj)∈Rnj×1为线性表示系数。

测试样本的类别还未确定，所以将整个C类手势样本构成一个冗余字典矩阵A=［A1A2…AC］∈Rm×n，则y可由A表示：

其中，x=[0 … 0 vj,1vj,2… vj,nj0 … 0]为测试样本的稀疏系数，非零元素均对应第j类，非零元素左侧含有零元素nj(j-1)项，右侧含零元素有nj(C-j)项，若稀疏度S=||x||0且S≪n，则认为x是稀疏的。

1.2 最小化范数的稀疏计算方法

因为字典A的维数小于样本数，即m＜n，所以式（2）属于欠定方程，解不唯一。但x是稀疏矩阵，且A满足2S阶约束等距性质（restricted isometry property，RIP），即A中任意2S列样本数据线性无关，对于任意样本y和常数δS∈（0，1），字典A满足

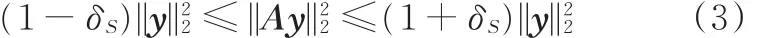
则可以保证有唯一解［16⁃17］。

式（2）可以通过最小化l0范数求解：

但最小化l0范数的求解是个NP⁃hard问题，只能近似求解，为提高计算精度，可以将l0范数求解稀疏系数问题转化为最小化l1范数问题进行分析。根据压缩感知理论，当x足够稀疏时，式（4）可以等价于求解最小化l1范数问题［18］：

实际的样本采集会受到噪声、光照等影响，从而影响测试样本和训练样本的相关性，进而影响识别率。为提高鲁棒性，可以添加噪声约束：

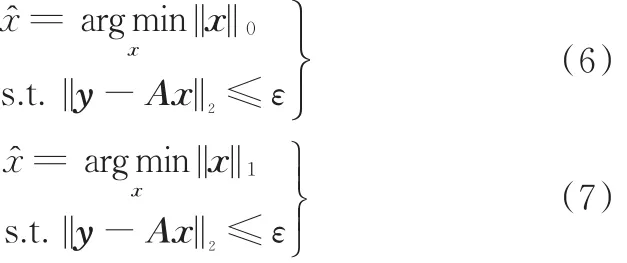
1.3 最小残差的分类

线性组合的稀疏系数已求得，那么可以利用稀疏系数和冗余字典重构测试样本，然后比较每个类的重构样本和测试样本：

式中，γj(y)为第j类样本对应的残差；δj(x^)为x^中第j类样本对应位置的系数值，其他位置的系数值为0；I(y)为测试样本的类别。

根据最小残差判断测试样本的类别。

SRC算法的步骤总结如下：

（1）输入训练样本 A∈Rm×n，测试样本 y∈Rm，误差阈值ε＞0；

（2）对A的每一列和y进行l2范数归一化；

（3）求解最小化l0范数问题：

或转化为求解最小化l1范数问题：

（4）对j类样本计算残差：

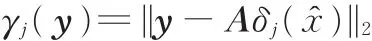
（5）输出类别I(y)=argminjγj(y)

2 改进的自适应正交匹配追踪算法

本文利用原子匹配测试来估计初始的稀疏度，该稀疏度S0小于真实的稀疏度S。将u=前S0个较大值对应的索引构成集合Λ0，其中，γ0为初始残差，Al为训练样本的第l列，对应A的列构成矩阵A0。文献［17］提出一个真命题，即A以参数(S,δS)(δS∈(0,1))满足受限等距性

稀疏表示理论中，稀疏系数的求解至关重要，即如何利用冗余字典中的少量原子表示原信号［19］，本文针对各种贪婪算法的缺点，为提高算法的精度和效率，提出改进的自适应正交匹配追踪(MACMP)算法。MAOMP算法无需输入真实稀疏度，而是先通过匹配测试来估计稀疏度初始值，将满足条件的估计值作为支撑集的长度；然后从投影集合中筛选原子，并更新索引集和支撑集，利用回溯思想和最小二乘法估计原始信号，更新残差；最后分阶段和变步长地调整筛选的原子数，逼近真实稀疏度，从而进行更好的稀疏表示。

2.1 稀疏度估计

2.2 变步长

由于稀疏度一般是未知的，而SAMP算法采用较小步长逼近且步长固定，这便降低了算法效率。由于每次迭代残差是不断下降的，刚开始下降较快，之后幅度逐渐减缓，最后趋于稳定值，因此步长也应该逐渐减小，即开始时，采用较大步长以减少迭代，然后逐渐减小步长、提高精度。本文实现变步长采用的方法是，在满足变步长条件时给步长lstep乘以一个步长系数β∈（0,1），随着阶段nstage的增加，步长lstep逐渐减小，即

整个MAOMP算法的步骤如下：

（1）输入训练样本A∈Rm×n、测试样本y∈Rm、常数δS、步长系数β。

（2）初始化。稀疏度S0=1，步长lstep=m/lbn，残差γ0=y，索引（列序号）集合Λ0=∅，索引集合对应的支撑集合A0=∅。

（3）计算投影集合u={uj|uj= ||γ0,Al,l=1,2,…,n}，选择u中的前S0个较大值，并将其索引值和支撑集分别存入Λ0和A0。

（7）求解y=Agxg的最小二乘解x^g=

（8）从x^g中选出绝对值最大的L项记为x^gL，对应的索引构成集合ΛgL，对应A的列构成集合AgL；

（10）如果残差 ||γg||2＜ε，则转步骤（11）；L+lstep，g←g+1，转步骤（5）；如果两个条件都不满足，则Λg= ΛgL，g←g+1,转步骤（5）。

（11）输出稀疏系数x^，其中索引集合Λg对应位置的非零项为最终迭代后的x^g。

MAOMP算法和SAMP算法类似，输入参数不需设定稀疏度，步骤（2）～步骤（4）为估计稀疏度过程，初始化支撑集的长度为所估计的稀疏度S0，提高了算法效率，另外，不同情况下的初始步长也不同，这里设定lstep=m/lbn。步骤（5）～步骤（10）为基于SAMP算法的分阶段逼近过程，根据条件逐渐改变步长可以更好地逼近真实稀疏度，从步骤（10）可以看出，每次迭代后的残差不断减小，因此算法能够收敛。MAOMP算法采用稀疏度估计和变步长在一定程度上减少了迭代次数并提高了精度。

3 实验结果仿真分析

3.1 手势样本库的建立

为验证本文方法对手势的识别效果，需采集手势图像，建立手势样本库，分析各因素对手势识别的影响情况。实验时选取指定的手势样本，在YCbCr彩色空间建立椭圆模型进行手势分割，并提取Hu不变矩和HOG特征。

3.1.1 抓取手势样本库

本文采用摄像头采集5个人的5类典型的抓取手势样本，即五指抓、三指抓、两指捏、单指钩和张开，如图1所示，每人采集5类手势各20张，即每类手势采集100张，共500张图像用于实验，采集手势的过程中，考虑手势旋转、尺度、光照和背景的变化。

图1 五类抓取手势样本Fig.1 Five kinds of grasping gesture samples

3.1.2 ASL样本库

ASL样本库包含26个字母的手势（字母j和z的手势是动态的，所以本文不予考虑），这些手势图片采用Kinect在相同光照和场景下分别对5个人进行采集，每个操作者及每个字母都有颜色图和深度图，其中，每人采集24个字母的彩色图像各20张，彩色图像共2 400张可用于实验。

3.2 参数选择对MAOMP算法性能的影响

为验证稀疏度的估计效果，比较参数δS取不同值时稀疏度S的估计值。实验时，抓取手势样本库中，每类手势随机选取50个训练样本、10个测试样本，并降维到100；ASL样本库中，每类手势随机选取50个训练样本、2个测试样本，并降维到100，实验结果如图2、图3所示。

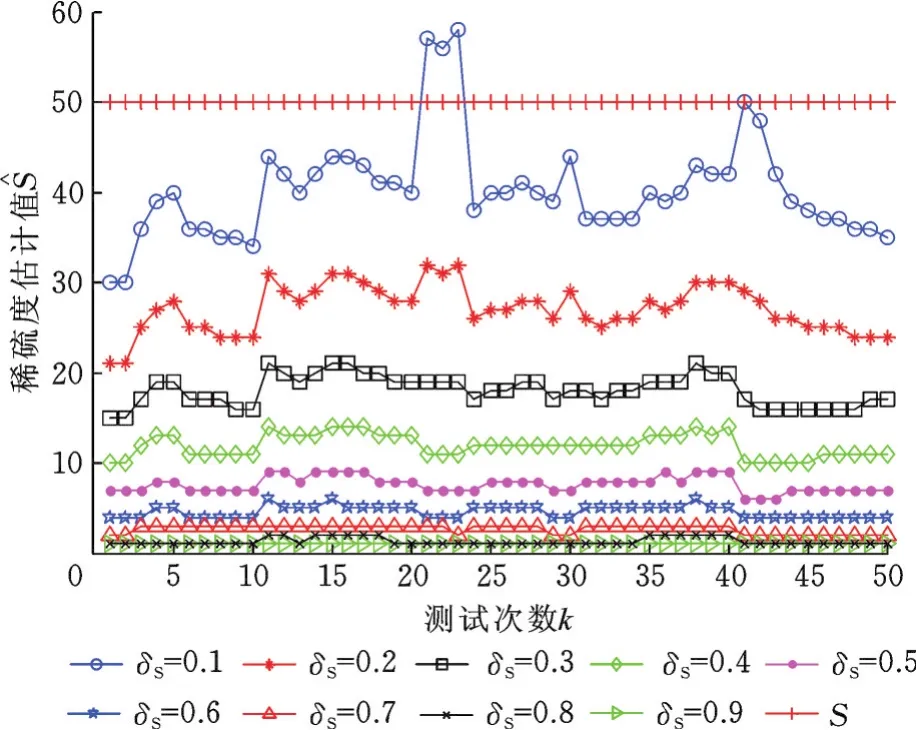
图2 抓取手势样本库上的稀疏度估计Fig.2 Sparsity estimation in grasping gesture sample database

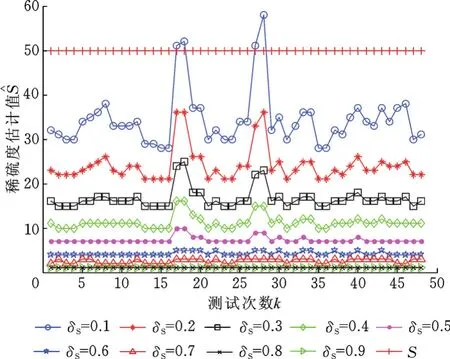
图3 ASL样本库上的稀疏度估计Fig.3 Sparsity estimation in ASL sample database

由图2、图3可以看出，每个δS对应的稀疏度估计值S0都在某个值附近波动，比如δS=0.2时，在抓取手势样本库上，估计值S0的平均值为27，在ASL样本库上，估计值S0的平均值为24；由于在两个手势库上每类训练样本均取50个，所以理论稀疏度S=50可作为稀疏度估计的参考。δS的值越小，稀疏度的估计值越大，波动越大，与理论稀疏度越接近，但估计值可能会大于理论稀疏度；δS的值越大，稀疏度的估计值越小，估计值越稳定，但小到一定程度后，如当δS=0.9时，稀疏度估计值保持致迭代终止条件的范围增大，从而增加了迭代估计，稀疏度估计值便较大，反之亦然。所以为减少后续迭代，并防止过估计，本文选取δS=0.2。

下面通过实验验证不同β值对算法的影响。在抓取手势样本库上，每类选取50个训练样本，剩余样本作为测试样本，并将特征降维到100；在ASL样本库上，每类选取50个训练样本，剩余样本作为测试样本，并将特征降维到100，δS取0.2。

图4所示为不同的步长系数对识别率的影响，可以看出，随着步长系数β的增大，两个样本库上的识别率都逐渐降低。抓取手势库上，随着β的增大，识别率从93.2%降到79.5%；ASL样本库上，随着β的增大，识别率从94.9%降到80.2%，而且在β=0.4和β=0.5之间降的幅度最大，约为4%，其他区间降的幅度约为2%。

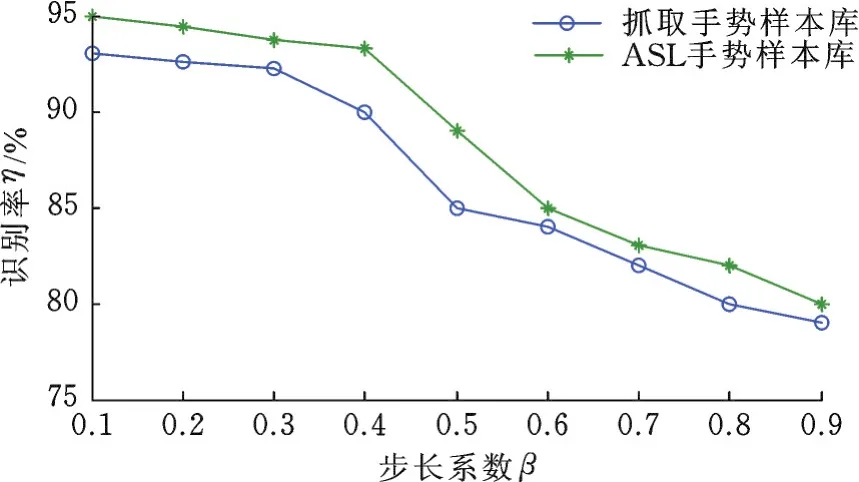
图4 不同的步长系数对识别率的影响Fig.4 The influence of different step size coefficients on recognition rate

β=0.4和β=0.5之间识别率的降幅最大，为更好说明其情况，在两个样本库上各迭代100次和150次，绘制了β取不同值时残差随迭代次数的变化曲线，如图5、图6所示。当迭代次数增加到一定值后，残差收敛于某个较小值。图5和图6中，残差保持不变时对应的迭代次数即为阶段数，并且随着步长系数的增大，阶段数减小，迭代次数也会减小，抓取手势库上的迭代次数最大值为88，最小值为9，在ASL样本库上的迭代次数最大值为103，最小值为14。由图5和图6可以看出，β=0.4和β=0.5之间迭代收敛次数下降的幅度比其他区间大，抓取手势库上的降幅为18，ASL样本库上的降幅为22，其他区间的降幅约为10。因为步长较大使得选取的元素较多，支撑集的长度较大，收敛快，但容易造成稀疏度的过估计从而使识别率降低，β=0.5时，已经造成过估计，对测试样本进行线性表示的原子中包含过多其他类原子，从而降低了识别率。综合考虑识别率和迭代次数，β取0.4较合适。

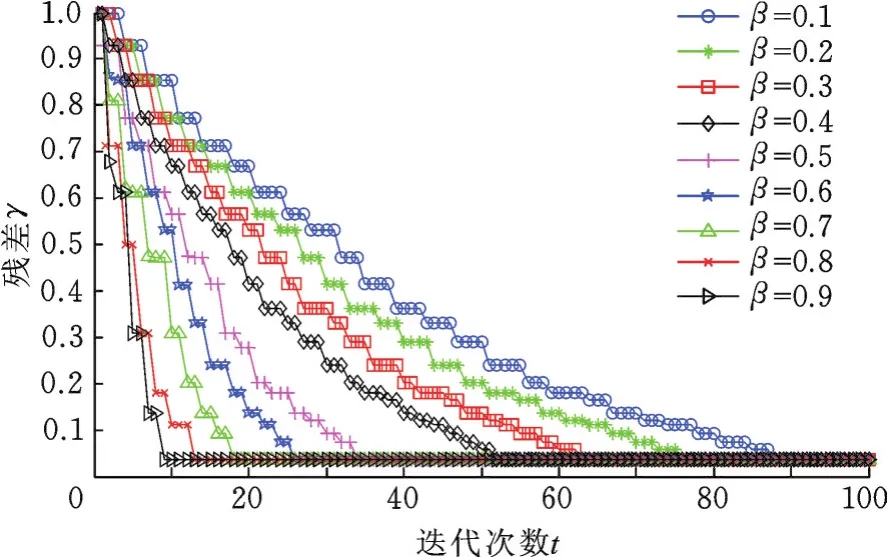
图5 抓取手势样本库上残差随迭代次数的变化情况Fig.5 The variation of residual error with iterations in grasping gesture sample database

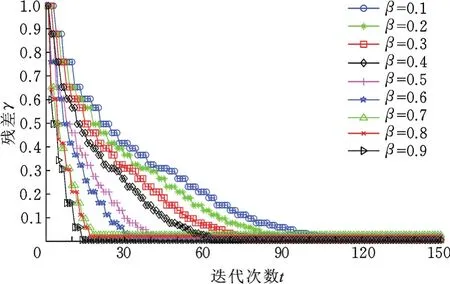
图6 ASL样本库上残差随迭代次数的变化情况Fig.6 The variation of residual error with the iterations in ASL sample database

3.3 算法的性能比较

分别在两个手势库上从识别率和平均运行时间两方面对MAOMP算法与OMP、ROMP、SWOMP、SP、SAMP算法进行比较分析。实验时每类随机选取50个样本作为训练集，50个样本作为测试集，分别提取特征后采用主成分分析法进行降维。另外需设定各算法的参数，MAOMP算法中δS=0.2，β=0.4，OMP、ROMP、SWOMP、SP算法的稀疏度设定为40，SWOMP算法的门限参数设定为0.5，SAMP算法的步长设定为5。

抓取手势样本库上不同匹配追踪算法的识别率和平均运行时间随维数的变化情况分别如图7、图8所示。由图7可以看出，各算法的识别率都随维数的增大而增大。低维数（m≤70）时，MAOMP算法的识别率仍能保持在85%以上，SAMP、SP、SWOMP算法识别率保持在80%～85%，而ROMP和OMP算法则小于80%；高维数（m＞190）时，MAOMP、SAMP、SP、SWOMP的识别率均达到90%以上，ROMP和OMP算法在85%左右。总体上看，同一维数下MAOMP算法的识别率最高，SAMP算法次之，OMP算法最小。由图8可以看出，随着维数的增大，各算法的平均运行时间逐渐延长。低维数时，各算法的平均运行时间都较短，在1 ms左右，相差较小。高维数时，各算法运行时间相差较大，其中维数为200时，OMP算法的平均运行时间达到28 ms，SAMP算法为19 ms，MAOMP算法为12 ms，其他算法几乎在10 ms以下。总体上看，同一维数下OMP算法的平均运行时间最长，SAMP算法次之，SWOMP算法最短。

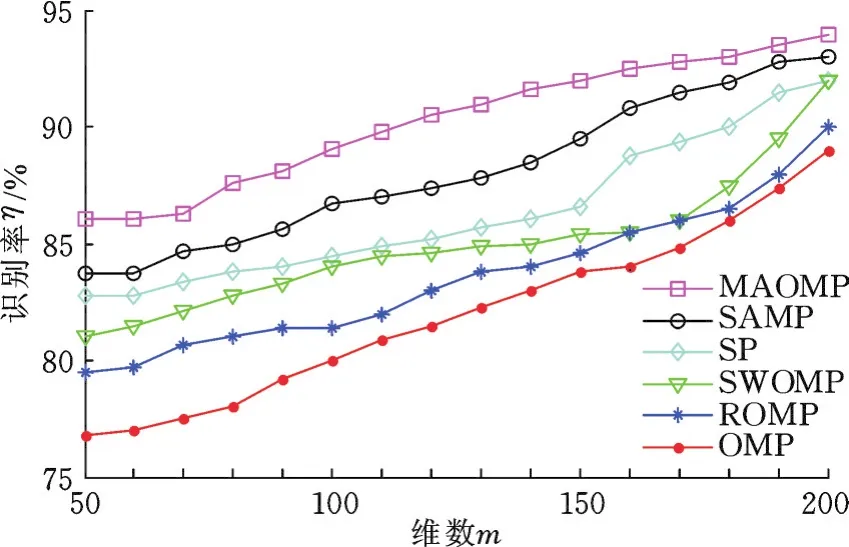
图7 抓取手势样本库上各算法的识别率随维数的变化情况Fig.7 The variation of recognition rate on each algorithm with the dimensionality in grasping gesture sample database

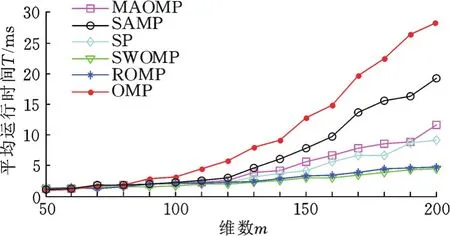
图8 抓取手势样本库上各算法的平均运行时间随维数的变化情况Fig.8 The variation of average run time on each algorithm with the dimensionality in grasping gesture sample database

ASL样本库上不同匹配追踪算法的识别率和平均运行时间随维数的变化情况分别如图9、图10所示，可以看出，识别率和平均运行时间都随维数的增大而增大，由于在ASL样本库上选取样本较多，所以与抓取手势库相比，识别率相对较高，平均计算时间相对较长。图9中，低维数（m≤70）时，MAOMP、SAMP和SP算法的识别率都在85%以上，SWOMP、ROMP和OMP算法的识别率保持在80%～85%；高维数（m＞190）时，MAOMP、SAMP、SP、SWOMP的识别率超过90%，ROMP和OMP算法在85%～90%；同一维数下，MAOMP算法的识别率最高，SAMP算法次之，OMP算法最小。图10中，在低维数时各算法的平均运行时间都较短，在2 ms左右，高维数时各算法运行时间相差较大，其中维数为200时，OMP算法的平均运行时间达到54 ms，SAMP算法为34 ms，MAOMP算法为25 ms，其他算法都在20 ms以下；同一维数下，OMP算法的平均运行时间最长，SAMP算法次之，ROMP算法最短。

图9 ASL样本库上各算法的识别率随维数的变化情况Fig.9 The variation of recognition rate on each algorithm with the dimensionality in ASL sample database

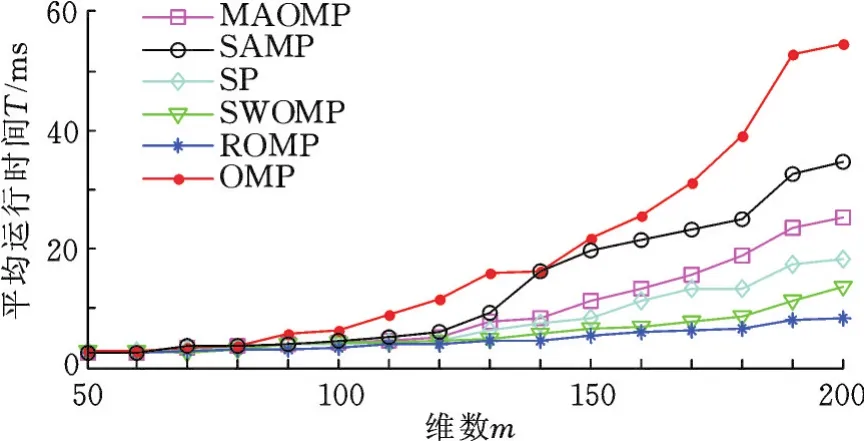
图10 ASL样本库上各算法的平均运行时间随维数的变化情况Fig.10 The variation of average run time on each algorithm with the dimensionality in ASL sample database

综上所述，OMP算法每次迭代只选取一个原子，导致精度和效率较低；SP、SWOMP和ROMP算法通过改进原子选择策略，每次直接选取多个原子，简化了OMP算法，提高了OMP算法的效率，但识别精度易受稀疏度或阈值的影响；SAMP算法通过步长逐步逼近，提高了OMP算法的精度，效率比OMP算法高，但由于依赖于初始步长的设定且步长固定，使得稀疏度估计不够准确，所以其识别率低于MAOMP算法；MAOMP算法在求解前引入了稀疏度的初步估计方法，后续每个阶段步长逐渐减小，使得逼近的稀疏度更加精确，比其他改进的OMP算法要高，平均运行时间也明显短于OMP算法和SAMP算法，样本较多、维数较高时，优势更明显。

4 结论

本文基于稀疏表示分类算法，针对稀疏求解算法中各贪婪算法存在精度低、参数不确定的问题，提出改进的自适应正交匹配追踪（MAOMP）算法。MAOMP算法引入稀疏度估计步骤，通过匹配测试来估计稀疏度初始值，并增加变步长步骤，分阶段调整筛选的原子数，逼近真实稀疏度。实验结果表明，MAOMP算法的性能比其他改进的OMP算法好，样本较多、维数较高时的优势更明显。下一步将加入一些遮挡图像进行识别来验证算法的鲁棒性。