基于动态差分元胞多目标遗传算法的混合作业车间布局改善与优化

王亚良 钱其晶 曹海涛 金寿松

浙江工业大学机械工程学院，杭州，310014

0 引言

TOMPKINS等［1］指出企业物料搬运成本占制造成本的20%～50%。对企业物流系统研究领域重要程度的评价调查表明，车间布局设计位居第一位，其次是车间物流调度与绩效评价、企业物流战略、企业物流网络重构及环境，合理的车间布局能降低10%～30%的制造成本［2⁃3］。

车间布局问题是NP⁃hard问题，随着设施数量的增加，传统的最优化算法（如线性规划、整数规划和分支定界法等）寻求精确解的可行性很低，智能优化算法能够在有效时间内寻求问题的近似最优解。LEE等［4］用遗传算法解决多层车间布局问题。郑永前等［5］用协同粒子群算法进行单元布局多目标优化。牛占文等［6］应用遗传算法对双行车间进行多目标布局改善优化，以物料搬运成本、设备单元移动成本、生产效率为优化目标，建立的模型更加贴近实际生产状况。为了避免动态环境下频繁进行车间布局，降低车间运行成本，刘琼等［7］建立了以车间物料搬运费用和面积费用最小化为目标的多目标鲁棒性布局优化模型，并用改进的蛙跳算法求解该模型。马淑梅等［8］采用模糊理论描述产品的不确定性，在遗传算法中引入局部自适应机制，对多行设备进行动态布局优化。上述学者都采用将多个分目标加权转化成为一个综合目标的研究思路。李爱平等［9］建立了物流搬运费用、非物流关系以及面积利用率的车间多目标模型，并采用非支配排序遗传算法（NSGA⁃Ⅱ）对模型进行求解。张屹等［10］利用差分元胞多目标遗传算法（DECell）对多行车间布局进行优化，并与其他算法进行了比较分析，取得了较好的结果。黄君政等［11］对多个计划期内需求可预测的车间动态设备布局问题进行研究，采用NSGA⁃Ⅱ对建立的多行车间布局模型进行多目标优化。左兴权等［12］针对双行设备布局既具有组合方面（设备排序）又含有连续方面（设备精确位置）的特点，将多目标免疫算法（MIA）和线型规划方法结合起来，为获取双行设备布局非支配解集提供新方法。SARAS⁃WAT等［13］在传统布局目标的基础上，增加了平均在制品库存量这个新目标，用模拟退火算法对块布局问题进行多目标优化。SEIFBARGHY等［14］考虑不同搬运设备对物料搬运的影响，提出一种用于动态设备布局的多目标水流算法。

求解车间布局模型大多采用遗传算法［4,15］、粒子群算法［5,16］、差分进化算法［10］、混合算法［17］以及多目标转化成单目标算法，但在求解布局多目标优化特别是混合作业车间布局问题时还存在不足，其求解质量有待进一步提升。本文对混合作业车间布局的原型特征进行分析和研究，重点描述车间场地的制约性、混合生产方式的协同性、作业单元类型的多样性、物流路径及搬运费用的集约性及非物流关系等原型细节，建立混合作业车间多目标布局模型，并用提出的动态差分元胞多目标遗传算法对其进行优化。

1 多目标混合作业车间布局模型

1.1 多目标函数

布局时，假设车间和作业单元均为矩形结构，车间大小和作业单元大小均已知，混合作业车间布局如图1所示。车间的长度为a，宽度为b；作业单元i的长度为Li，宽度为Wi；作业单元水平方向（沿x轴方向）的最小间距为hmin，垂直方向（沿y轴方向）的最小间距为vmin。

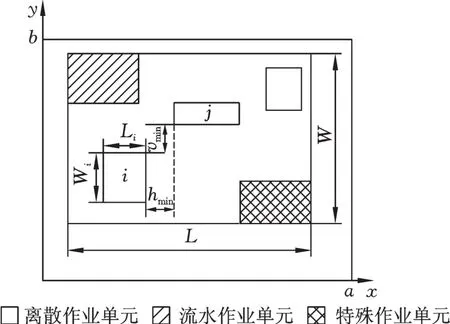
图1 大型混合作业车间布局示意图Fig.1 Schematic diagram of the large hybrid workshop layout

1.1.1 物料搬运成本最小

大型混合作业车间生产的产品多、工艺路线复杂且交叉频繁，须根据不同产品组合选择合理的生产工艺路线以减少物料搬运成本：

式中，n为布局的作业单元数目；cij为综合考虑物料大小、搬运工具和搬运载荷等因素的作业单元i到作业单元j的单位物料搬运成本；fij为作业单元i到作业单元j的总物料搬运件数；dij为作业单元i到作业单元j的物料搬运距离。

1.1.2 作业单元移动成本最小

针对不同的生产需求，部分作业单元将重排组合，其函数表达式为

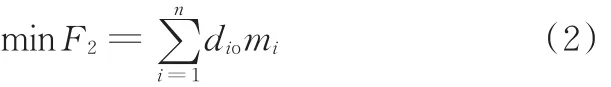
式中，dio为作业单元i前后移动的曼哈顿距离（天车搬运为主）；mi为作业单元i的移动成本。

1.1.3 作业单元包络矩形面积最小

作业单元包络矩形面积函数表达式为式中，L为包络所有作业单元矩形的长度；W为包络所有作业单元矩形的宽度。

1.1.4 作业单元非物流关系最大化［4］

最大化优化目标可以转换成最小化优化目标，故

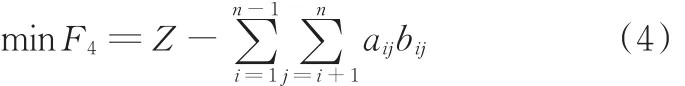
其中，Z为一个较大的数，保证F4为正数即可；aij为作业单元间的非物流关系邻接度，如表1所示；bij为作业单元间的非物流关系邻接度因子，如表2所示；dij_max为两个作业单元间的最大曼哈顿距离。

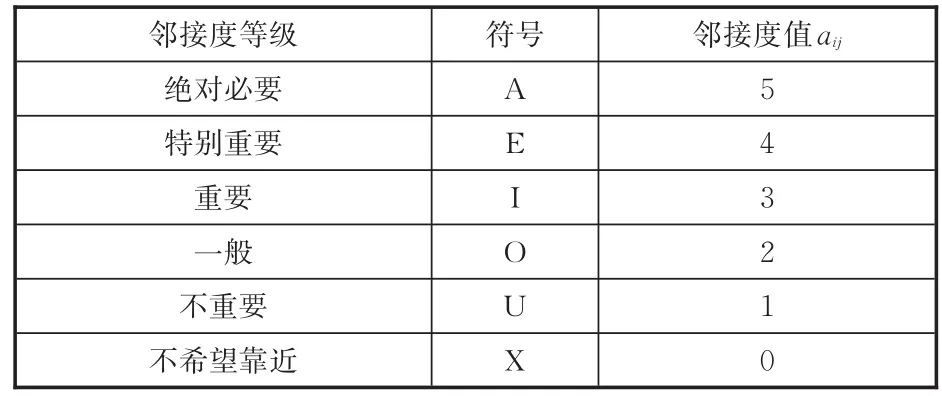
表1 作业单元间的非物流关系邻接度值Tab.1 Non”logistic relationship between units

表2 作业单元间的非物流关系邻接度因子Tab.2 Non”logistics relationship adjacency factor between units

因为第1个和第2个优化目标单位一致，因此，上述4个目标可以最终转化为3个优化目标：

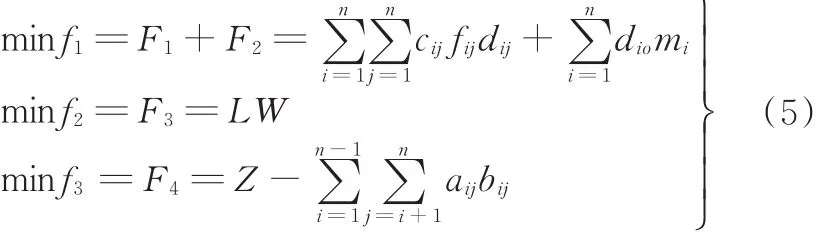
1.2 约束条件

多目标混合作业车间布局模型约束主要为间距约束、边界约束和特定约束。间距约束要求任意两作业单元之间保留一定的间距。边界约束要求任何作业单元必须在车间内。对于某些特殊作业单元，布局时要考虑其特殊要求，即特定约束。

（1）间距约束。任意2个作业单元在水平方向（x方向）的间距应不小于hmin或在垂直方向（y方向）的间距应不小于vmin，则应满足： ||xi-xj≥

（2）边界约束。各个作业单元在车间布局时，不能超出车间，其边界约束为

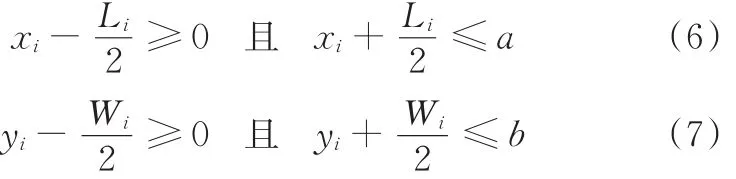
（3）特定约束。指混合作业车间中的特殊作业单元需满足的一些特定条件，本文的布局实例中，喷漆单元作为特殊作业单元，须靠近通风处。考虑现有硬件设施，在布局时对喷漆单元进行预置。喷漆单元的预定位置

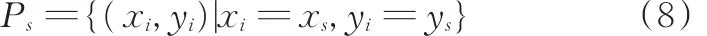
式中，(xs,ys)为喷酒保单元预置位置的坐标。

1.3 作业单元间的距离

在车间布局中，常采用曼哈顿距离来表示作业单元与作业单元之间的物料搬运距离。当2个作业单元之间无其他障碍单元时，采用曼哈顿距离来表示2个作业单元之间的物料搬运距离比较符合实际情况，曼哈顿距离的计算公式如下：

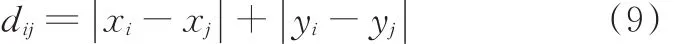
当作业单元之间有其他作业单元挡道时，用曼哈顿距离来衡量单元之间的物料搬运距离，会使得优化模型与实际情况的出入较大。为此，对曼哈顿距离进行修正。

如图2所示，作业单元i与作业单元j之间存在着曼哈顿距离，作业单元k是物料搬运路线上的障碍物，障碍物的数学表达式如下：

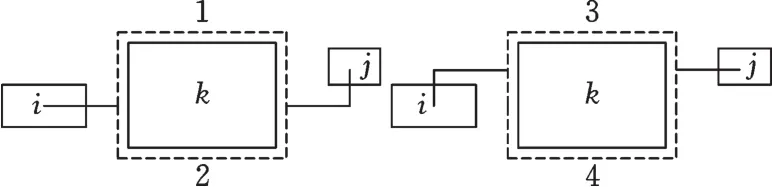
图2 作业单元之间有障碍情况Fig.2 Situation of obstacles between unit

为了绕开这些障碍物，在原先曼哈顿距离路线的基础上提取出4条新路线，并选取距离最短的路线来代替原先的物料搬运路线，修正公式如下：

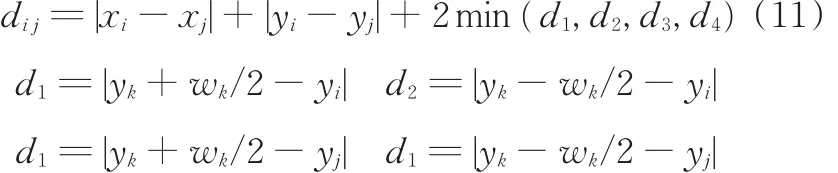
2 动态差分元胞多目标遗传算法设计

差分进化算法有多种变异方式，其中，差分元胞多目标遗传算法DECell的变异、交叉操作为

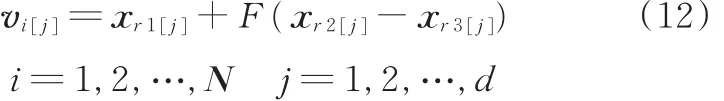
式中，vi[j]为父本向量xr1经过变异后得到的变异向量；xr1[j]、xr2[j]、xr3[j]为 3个第 j维决策变量的父本向量；r1、r2、r3为三个父本的索引位置；F为缩放因子；N为种群规模；d为解空间的维数。

交叉操作后获得的向量

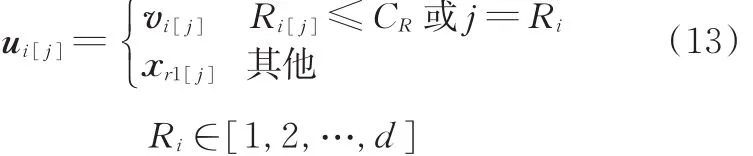
式中，Ri[j]为个体i的第j维决策变量在交叉操作过程中产生［0,1］之间均匀分布的随机数；CR为介于［0,1］间的交叉常量。

连续型车间布局模型中，布局的解有无穷多个，一旦某个解占优，则算法容易陷入局部最优。当算法获得的所有解陷入局部最优时，xr2［j］-xr3［j］趋于零。式（13）的变异方式不利于算法跳出局部最优［18⁃19］，导致算法无法进一步获得更好的布局方案，故当|xr2［j］-xr3［j］|小于某个值时，采用新的变异操作：

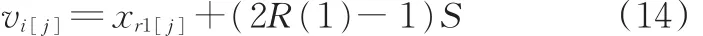
其中，R（1）为［0,1］之间均匀分布的随机数；S为变异步长，S=z（xr1[j]-u-xr1[j]-l）；xr1[j]-u、xr1[j]-l分别为父本向量xr1第j维决策变量的最大值与最小值；z为控制变异步长大小的系数，z较小，算法不易跳出局部最优；z较大，算法的收敛精度就差，这里取z=0.01。由于算法采用动态方式进行变异操作，故将这种变异方式称为动态变异。

将式（12）和式（14）结合，得到最终的变异方式（基于动态变异策略的变异）：

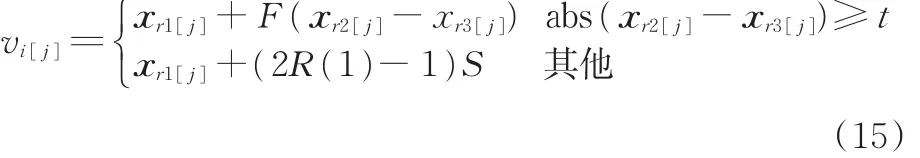
其中，t用来控制何时采用动态变异。采用动态变异的目的是使算法跳出局部最优。当作业单元间的坐标差小于0.5 m时，采用动态变异。将基于动态变异策略的变异引入到DECell中，得到动态差分元胞多目标遗传算法（DDECell）。

3 基于DDECell的车间布局优化主要步骤

算法的主要流程如图3所示，主要步骤如下：

（1）随机生成初始种群。采用实数制编码生成初始种群。将编码设计为［（U1，U2，…，Un），（x1，x2，…，xn），（y1，y2，…，yn）］，其中，Un表示第n个作业单元，（xn，yn）为第n个作业单元的坐标。（U1，U2，…，Un）是n个作业单元的一个全排列。

（2）选择父本。基于秩与拥挤距离，从当前个体的Moore型邻居结构中，通过二元锦标赛选出当前个体的2个父本。当2个邻居个体的秩不同时，选择秩小的邻居个体作为当前个体的父本。当2个邻居个体的秩相同时，则选择拥挤距离大的个体。

（3）变异交叉。对作业单元编号（U1，U2，…，Un）执行换位变异，即随机选择2个作业单元编号的序号，并进行互换。对（x1，x2，…，xn）、（y1，y2，…，yn）进行差分变异交叉操作。x、y坐标的变异交叉操作伪代码为

（4）子代评估。计算子代的目标函数值，如果子代支配当前个体，或子代与当前个体互不支配，但子代的拥挤距离大于当前个体的拥挤距离，则将子代替换当前个体，同时将这个子代加入外部文档。一旦非支配个体的数量超出了外部文档的规模，则将拥挤距离最小的个体删除。

（5）种群更新。重复步骤（2）～（4），完成网格中所有个体的进化操作。在每一代进化结束后，从外部文档中选一些个体代替相同数量的二维环形网格中的个体。继续进化，直至满足进化的终止条件。

图3 DDECell算法流程Fig.3 Flow chart of DDECell algorithm

4 混合作业车间布局实例

4.1 车间基本情况介绍

某吸尘器车间的总尺寸为160 m×60 m。车间内有注塑区域、原材料配送区域、电机组装区域、喷漆区域、丝印区域、烘干区域、手柄预装区域、地刷预装区域、尘杯预装区域、半成品区域、总装区域，共11个功能单元区域。作业单元的原始布局如图4所示。现对原有的布局方案进行改善优化。4号单元为喷漆单元，对其位置进行固定。矩阵C、F分别表示作业单元之间的单位物料搬运成本（以1个标准箱移动1 m所产生的搬运成本为基本单位）及物流量（单位：100标准箱）。作业单元之间的非物流邻接度如表3所示，各个单元的其他信息如表4所示。根据车间实际情况，须满足下列条件之一：作业单元之间水平距离hmin=2.5 m，垂直距离vmin=2.5 m。

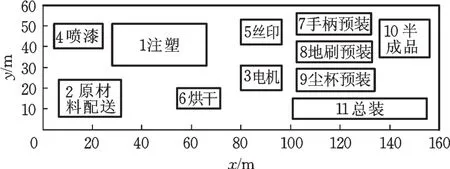
图4 作业单元原始布局Fig.4 Original layout of the unit

表3 作业单元之间的非物流邻接度Tab.3 Non-logistic relationship between units

表4 各个单元的其他信息Tab.4 Additional information for each unit

4.2 实例求解及结果分析

采用DECell和DDECell对车间布局进行优化。两种算法的参数设置如下：种群数量为100，外部文档储存容量为100，最大进化代数为2 500。为了较好地平衡算法全局探索与局部开发能力［20］，取缩放因子F=0.6，交叉常量CR=0.6。两种算法分别独自运行15次。

由于该优化问题是NP hard问题，故很难找到最优解集。为了展示方便，分别从DECell和DDECell获得的非支配解中，根据秩与拥挤距离提取50个支配解。图5描述了这些非支配解及原始布局对应的Pareto前端，由图可知，DECell获得解比较密集，DDECell获得的解的多样性要好于DECell。

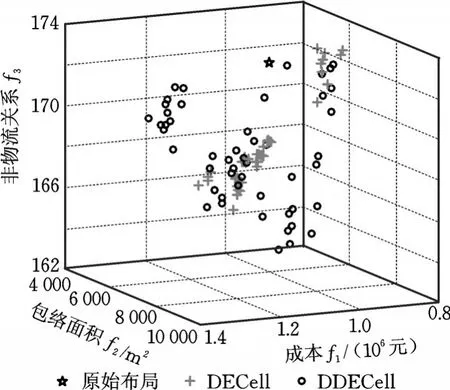
图5 两种算法获得的非支配解的Pareto前端Fig.5 Non”dominant Pareto obtained by the two algorithms

图6给出了优化问题的双目标Pareto前端，由图可知，DDECell获得的Pareto前端要比DECell的前端更靠近经两个坐标轴，这表明DDECell的收敛性要好于DECell。

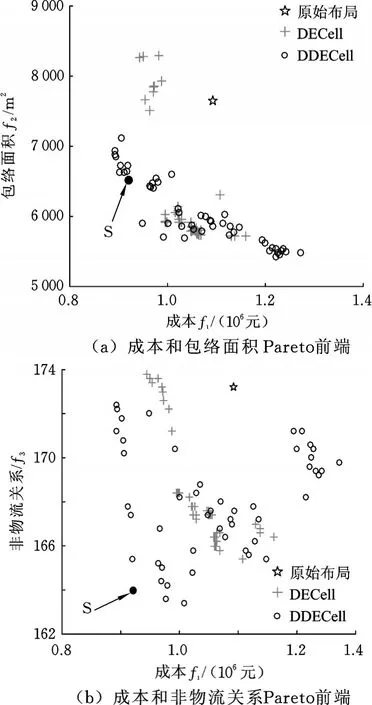
图6 双目标Pareto前端Fig.6 Pareto front of two objectives

由图5和图6可知，采用动态变异的差分元胞算法在多样性和收敛性上都要优于差分元胞算法，这证明了动态变异的有效性。从DDECell算法获得的50个非支配解中，提取的3个优化目标都优于原始布局的解（S标示的解）。车间布局实例是一个多目标优化问题，即3个分目标是无法同时达到最优的。由图6a可知，作业单元的包络面积f2比较大；由图6b可以看到，S的成本f1和非物流关系f3都比较好。图7所示为S对应的布局方案，可以发现原材料配送区域2、电机组装区域3、半成品区域10离总装区域11都很近，这有利于吸尘器的总装。4号喷漆单元与5号丝印单元离6号烘干区域较近，这兼顾到了这些单元间的工艺联系，体现了非物流关系的最大化。表5给出了S对应解的具体信息。通过表5可知，经优化后，新的布局方案的3个分目标都优于原始布局。

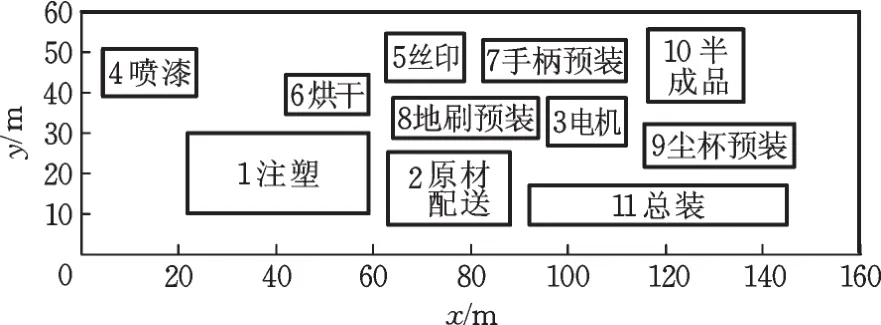
图7 S对应的作业单元布局Fig.7 Layout of optimal solution S

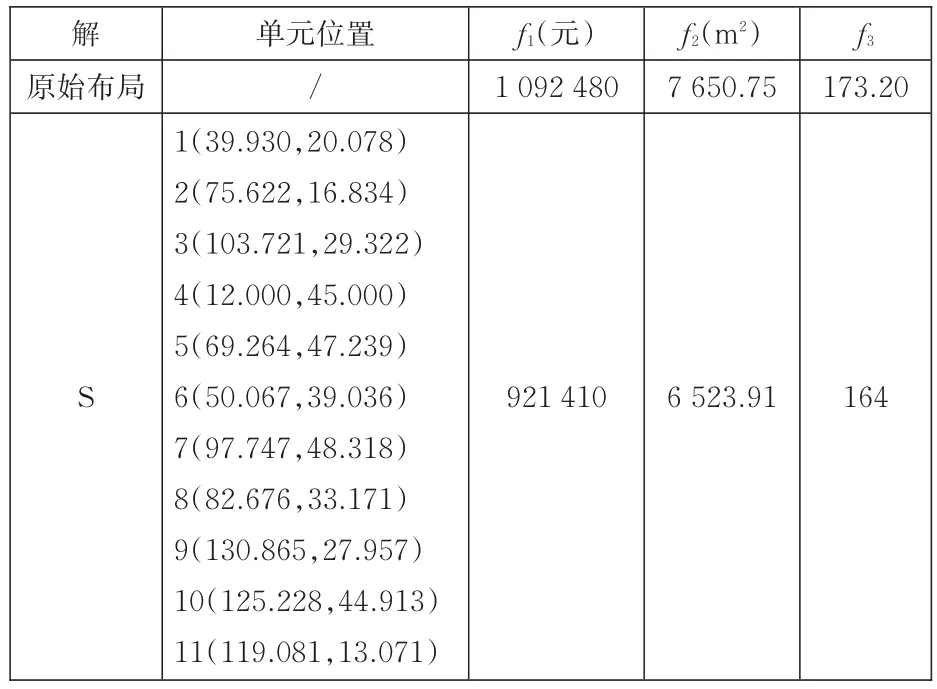
表5 S对应的作业单元布局Tab.5 Unit layout of optimal solution S

5 结论

（1）提出了一种基于动态差分元胞多目标遗传算法的混合作业单元布局改善优化新方法。在构建布局模型时，考虑实际的生产情况（特殊单元的特定处理、作业单元的移动成本、物料搬运路径等），对原有布局进行优化。

（2）在满足约束条件的前提下，作业单元可以随机布置在车间的任何一个位置，这增加了算法寻优的难度，同时也容易使算法陷入局部最优，降低算法的搜索效率。在差分元胞多目标遗传算法中引入动态变异策略，有助于算法跳出局部最优，寻找更优的布局方案。