基于瀑布机制的重载机械手自组织精密模式

马翔宇 罗天洪

1.西安航空学院机械工程学院，西安，710077 2.重庆交通大学机电与车辆工程学院，重庆，400074

0 引言

随着科学技术的发展，良好的生物特性为机器人的结构与功能设计提供了较多的参考，比如生物结构仿生、运动仿生等［1］。如何提高工业机器人的末端精度和稳定性，是复杂环境下机器人伺服控制的一个重要问题。影响机械手位姿精度的因素主要包括机器人零部件的加工误差、安装误差、传动误差、机器人关节的柔性及其工作环境等因素［2］。李宏凯等［3］对机器人生物控制中的中枢模式发生器（central pattern generator，CPG）网络进行了综述，并分析了其典型的数学模型。王炜等［4］针对仿肌肉驱动器在国内外的发展状况，从制作材料和机械装置、结构仿生、控制仿生以及在不同类型运动仿生机器人中的应用等方面进行总结和概述，并对其未来的发展趋势进行了预测。信继忠等［5］针对用串联机构设计的眼球转动机构无法解决眼球直径较小且需在其中放置摄像头的问题，采用空间RSSR机构设计了八自由度眼部机构，对眼球转动机构进行运动学分析，并在AD⁃AMS中进行运动学仿真，该眼部机构在保证眼球完整性的前提下，具有传动精确可靠、两个眼球独立控制的特点。杨永刚等［6］结合鹰翅翼的运动特点，提出了一种仿生扑翼结构，并在ADAMS中建立虚拟样机，通过分析与优化，获得满足设计标准的扑翼结构。

机械手的动力学问题日益突出，尤其在高速重载自动设备需求日益强烈的今天。高名旺等［7］为了在机构中实施内力控制，提出了一种基于功率优化的驱动力分配策略，并获得了机构内力和驱动力的变化规律。赵丁选等［8］针对遥操作工程机器人的主端受力不能准确反馈从端执行末端受力的问题，结合力反射型算法模型，提出了一种变增益力反馈算法。DONG等［9］针对高速重载码垛机的振动问题，提出一种描述码垛机对移动速度及承载能力反馈的数学方法，建立了一个法线方向的堆垛机械臂的动态静力学模型，根据叠加原理和虚功原理计算了末端执行器的正位移。罗天洪等［10⁃11］针对机械手关节处运动速度、角速度对精密机械手的影响，受生物神经元时空整合特点的启发，提出了基于神经元时空整合机械手的精密传递模式；针对宏-微机械手末端位姿、位置准确度的误差问题，受细胞学操纵子学说的启发，得出了基于操纵子模型的宏-微精密机械手运动的映射关系，仿真分析表明，由映射关系推导出的控制系统能够满足一定的精度要求［11］。张霞等［12］为提高穿戴式机器人在运动辅助过程中的人机交互柔顺性，提出一种以CPG为核心的协调控制方法，取得了良好的效果。随着科学技术的发展，诸多生物控制特性逐步被引入到机器人应用当中，然而，将瀑布机制运用到机械手精度控制尚未被研究。本文针对惯性力矩对机械手精度的影响，引入凝血原理的瀑布机制，提出基于瀑布机制的重载机械手自组织精密模式，以保证机械手在运动中尤其是在重载工况下获得更高的精度。

1 刚体惯性

动力学分析是机器人控制、结构设计与驱动器选型的基础。目前，机器人动力学分析最经典方法为拉格朗日法和牛拉法。将拉格朗日方程用于机器人时，必须将机器人连杆的动能、势能转化为关节转角和关节速度的函数，即要求建立连杆的质量分布模型。每一连杆都是刚体，所以刚体动能和势能可依据总质量和关于质心的惯量确定。

设V∈R3是刚体的体积，ρ(r)(r∈V,r为刚体的坐标)是物体的质量分布规律。若物体是均匀的，则ρ(r)就是常量ρ。刚体的质量可表示为质量密度的体积积分：

刚体的质心就是密度的加权平均，即

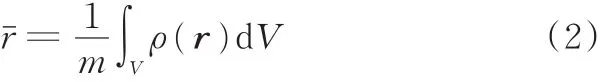
考虑图1所示的刚体（质心为C，刚体某一质量单元为q），其动能计算如下：在物体质心处建立一物体坐标系，并设g( )R,t ∈SE(3)为物体相对于惯性坐标系的运动轨迹，为简化起见，简略了所有下标。其中，R为旋转矩阵，表示观测坐标系与相对坐标系间的转换，t为时间。再设r∈R3为物体上一点相对于物体坐标系的坐标，rB表述物体上某一点在惯性坐标系下的坐标，则该点在惯性坐标系中的速度［13］

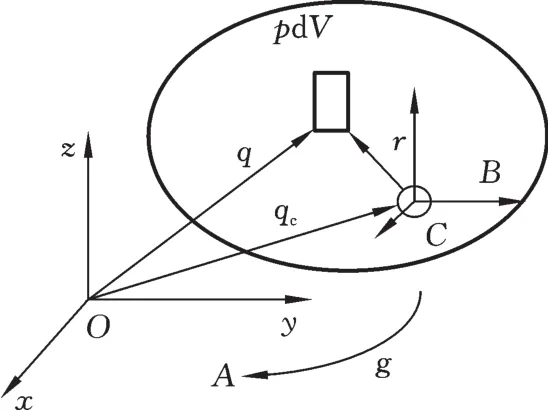
图1 刚体的惯性特性Fig.1 Rigid body of inertia

物体的动能

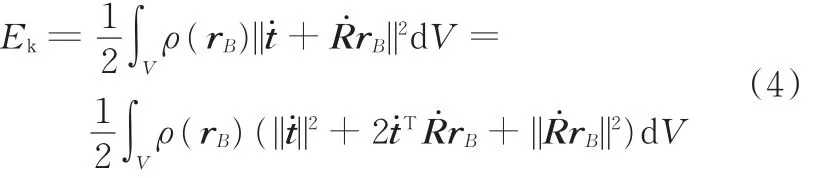
式（4）中的括弧里面的第一项为移动动能。由于物体坐标系位于质心，并且

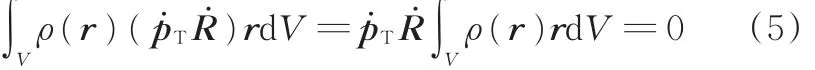
式中，pT为刚体上任一点坐标。

所以第二项为零，最后一项可利用转动特性和反对称矩阵加以简化：

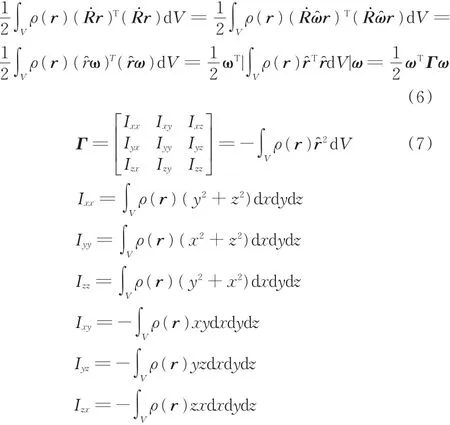
其中，ω∈R3为刚体角速度；对称矩阵Γ∈R3×3为在物体坐标系中表示的物体惯性张量。所以，物体总动能可写为移动动能与转动动能之和：

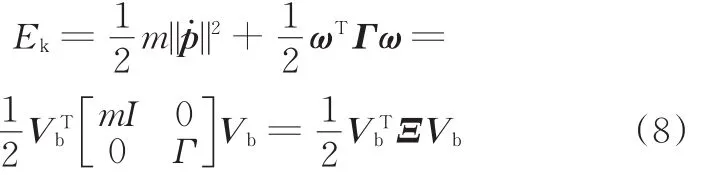
2 基于瀑布机制的重载机械手精度补偿

凝血过程一般包括两种途径：内源性凝血和外源性凝血，这两种途径的区别主要在于其启动方式及其对应的凝血因子，因而形成不同的凝血通路。凝血过程一般分为三个阶段：凝血活酶的形成、凝血酶原转变为凝血酶、纤维蛋白原转变为纤维蛋白，如图2所示。

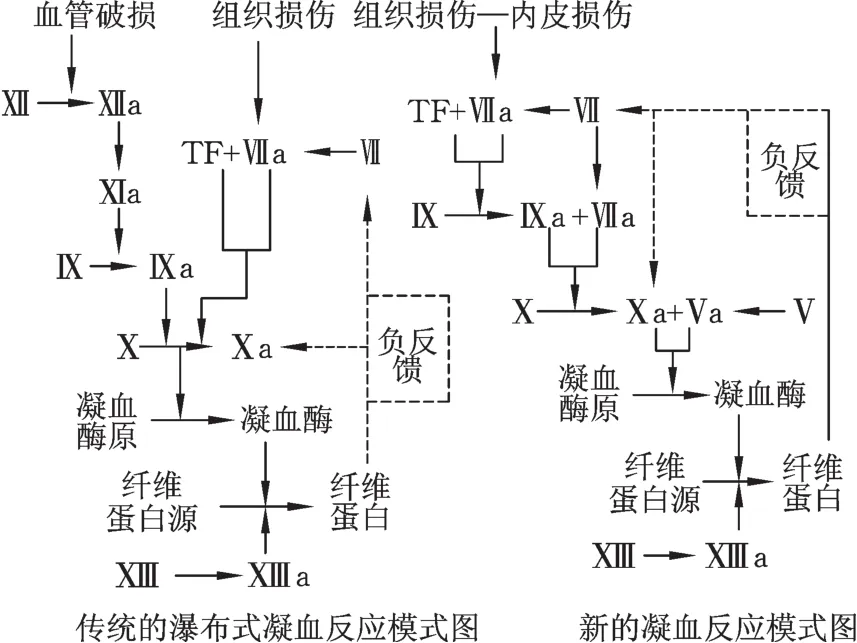
图2 血液凝固过程示意图Fig.2 Schematic diagram of blood coagulation

图2 介绍了传统瀑布式凝血反应模式和新的凝血模式，两种模式虽然结构形式不同，但其工作机理基本一致，本文主要对新型凝血反应进行探讨。图2中，Ⅹ表示Stuart⁃Prower因子，Ⅺ表示血浆凝血活酶前加速素，Ⅻ表示Hegemen因子，す表示纤维蛋白稳定因子，Ⅶ表示稳定因子，Ⅸ表示Chrismas因子，Ⅹa表示被Ⅹ因子被激活，同理，Ⅺa、Ⅻa、すa、Ⅶa等表示对应因子的激活因子。TF表示组织因子，广泛分布于身体各组织和器官，其主要作用是：当身体某一组织器官损伤时，凝血酶被TF激活。

当前存在一种比较普遍的观点，即外源性途径主要对凝血过程起启动作用，内源性途径对其起放大和支持的作用，其工作原理具体如下。

（1）启动环节。因子Ⅶa一旦与组织因子结合，激活因子Ⅸ和因子Ⅹ分别生成活化的因子Ⅸ（因子Ⅸa）和活化的因子Ⅹ（因子Ⅹa），在此环境下，因子Ⅹa将少量的凝血酶原转变为凝血酶，并激活血小板以及凝血中关键的辅因子（因子Ⅴ）。

（2）放大环节。在钙离子的参与下，因子Ⅸa在激活的血小板表面形成内在的活性酶，即活化因子Ⅹ的复合物。然后，凝血酶原酶复合物由因子Ⅹa与因子Ⅴa在被激活的血小板表面结合——这是一个钙离子依赖的过程；之后，此复合物激活凝血酶原，进而生成凝血酶，凝血酶与血小板分离后，将纤维蛋白转变为纤维蛋白单体。随着因子Ⅹa的进一步形成，形成更多的凝血酶，激活纤维蛋白原生成纤维蛋白并最终形成血栓。

（3）反馈环节。当伤口附近产生足够的血栓之后，组织因子形成抑制物TFPI，TFPI相继对Ⅹa和Ⅶa因子进行灭火处理，进而实现对凝血酶的控制，自动停止凝血的过程。

由上述得

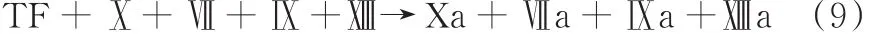
因相关凝血因子在组织因子的作用下，进一步被激活，变为对应的活化因子，所以，式（9）变为

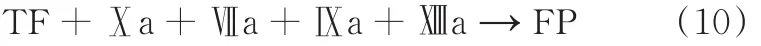
凝血过程在数个水平上受到调节。凝血过程的抑制物主要由组织因子途径抑制物（TFPI）组成。TFPI首先与因子Ⅹa复合并灭活Ⅹa，形成TFPI⁃Ⅹa复合物,然后，TFPI⁃Ⅹa的TFPI灭活与组织因子结合的因子Ⅶa，进而对凝血酶进行控制。

所以，TFPI抑制凝血的逻辑表达式为

由式（10）～式（12）得

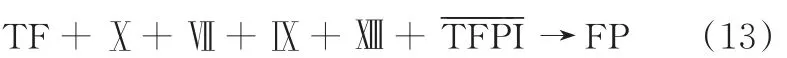
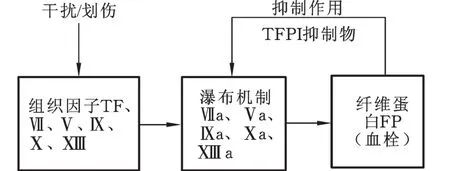
图3 瀑布机制机理Fig.3 Mechanism of waterfall

由图3可得：生物学中的瀑布机制的凝血原理具有完美的自动修复能力，当器官组织机构受到损伤时，其相关的组织因子在第一时间内被激活，并引起相应的连锁反应，进而激活凝血酶，以生成足量的纤维蛋白来保证正常的凝血过程；当划伤部位接近完成凝血过程时，由于组织因子抑制物TFPI的存在，将对相应的组织因子进行失活处理，以保证瀑布机制的反馈作用。

重载工况下，为保证机械手的工作精度和工作质量，关节运动常采用闭环控制系统进行作业。机械手正常作业过程中，外界干扰或其自身误差等原因会导致机械手各关节的输出力矩发生变化，进而影响关节的输出质量，此时需要机械手自身进行自我修正，依据自身的结构特点，对其各个关节进行组织协调，以保证机械手的高质量、高品质作业。

鉴于上述瀑布机制的凝血机理，结合机械手闭环控制的结构，本文得到了基于瀑布机制机械手自组织精密模式，如图4所示。

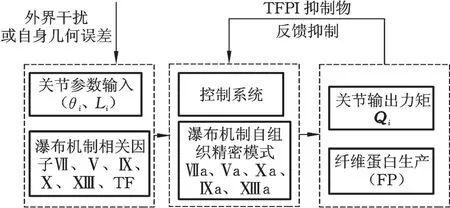
图4 基于瀑布机制的重载机械手自组织精密模式Fig.4 Self organizing precision model of heavy manipulator based on waterfall mechanism

由机械手动力学［13］可得

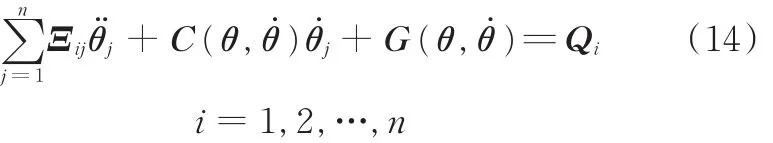
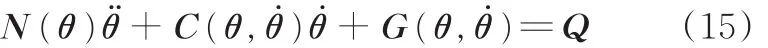
式中，对称正定阵N(θ)∈Rn×n为机械手惯性矩阵，

由式（13）、式（15）得机械手自组织精密数学模型：

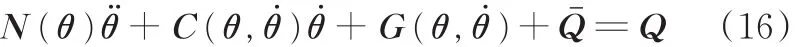
式中，Qˉ为自反馈，由其相关关节自组织协调获取。

3 仿真

为验证提出的自组织精密模式，选取机械手进行验证，建立的三维模型如图4所示。为简化计算，此处选取机械手的2个关节进行计算，如图5所示。设机械手连杆i为长方体杆，质量为mi，长度为li，B表示物体坐标系，S表示物体惯性坐标系，则各杆件的广义惯性矩阵为

图5 重载机械手三维模型Fig.5 3D model of heavy manipulator

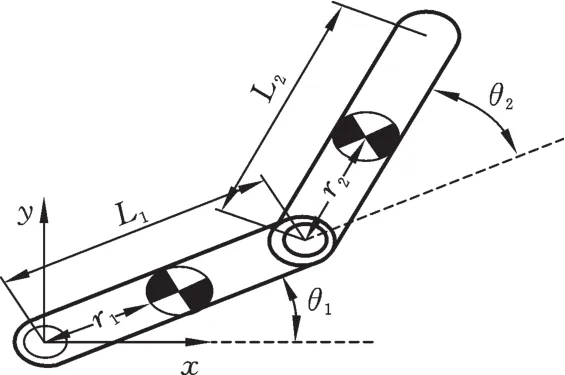
图6 机械手2关节简图Fig.6 Schematic diagram of 2 joint manipulator

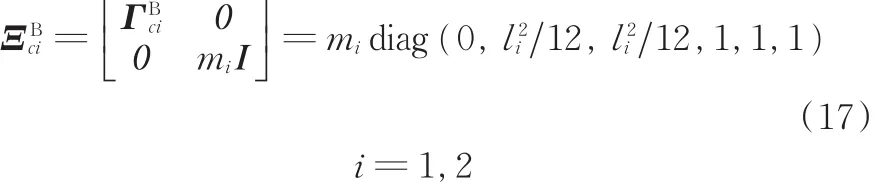
依据物体坐标系下的刚体广义惯性矩阵可得刚体惯性坐标系下的广义惯性矩阵［13］：

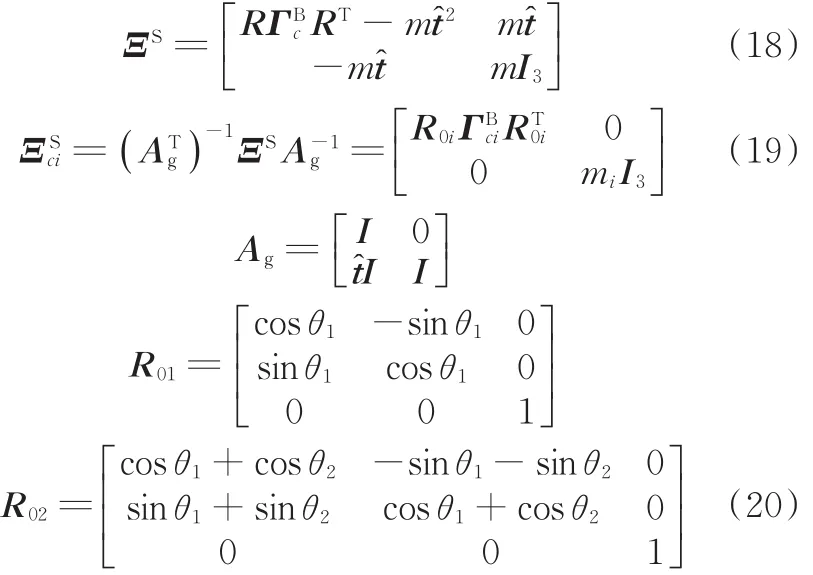
其中，t^是位置矢量t的伴随表达，且为一个反对称矩阵；I为单位矩阵。

由式（17）～式（20）联合求解得

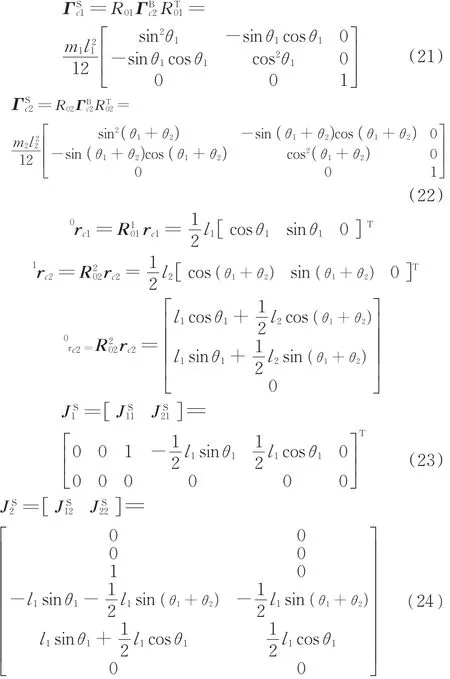
机械手的惯性矩阵

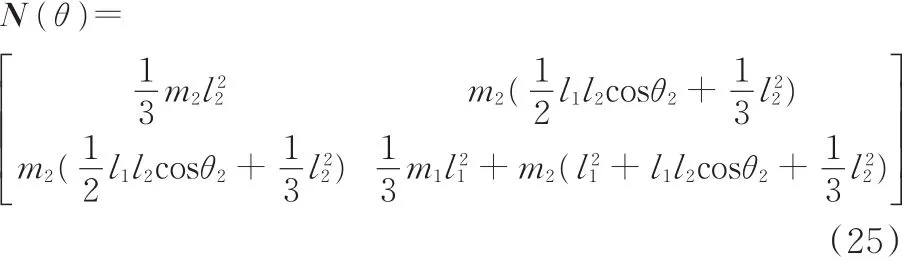
机器人重力项的影响：

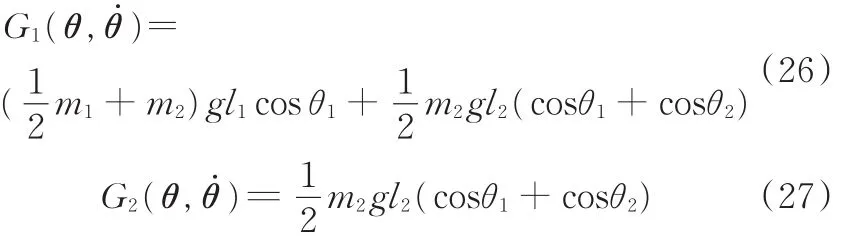
机器人的哥氏力与离心力：

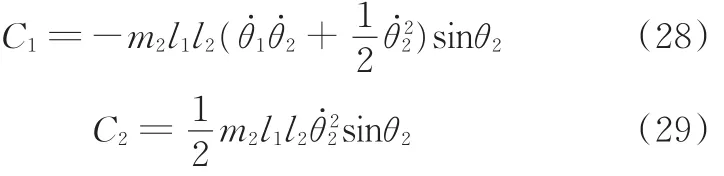
驱动项：

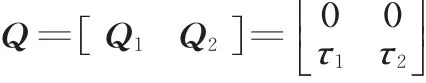
将式（1）～式（5）代入式（15）得

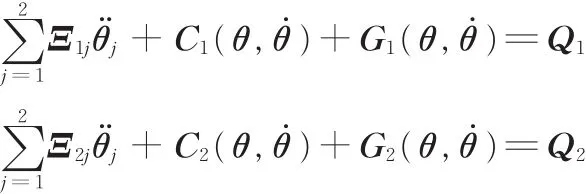
即得关节1、2作业时的各个关节输出力矩：

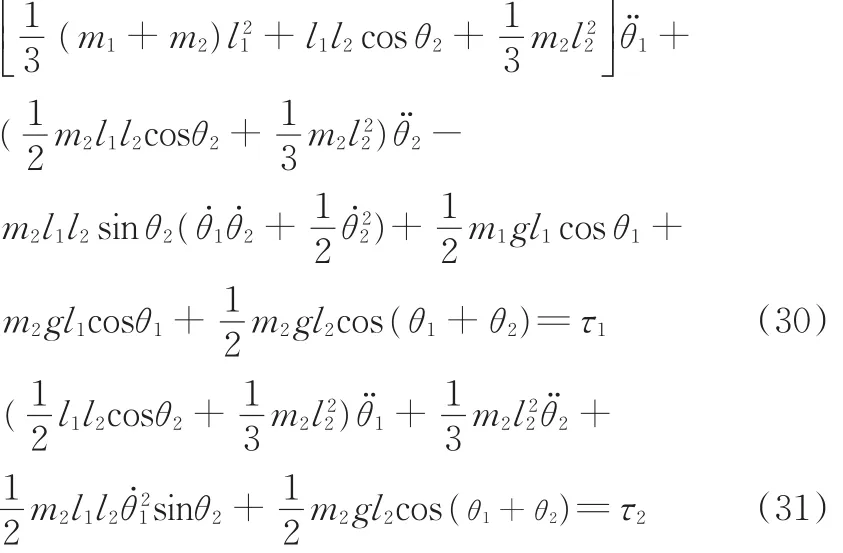
由式（30）、式（31）知，各个关节的力矩输出由关节长度及其对应的运动角度组合而成。机械手作业时，在加速/减速过程中，各个关节的输出力存在误差，进而影响关节输出的加速度和速度，甚至给机械手的末端精度带来一定的误差。为简化计算，此处仅对关节制造误差Δl对机械手关节输出力矩的影响进行分析。

将两关节参数：m1=5 kg，m2=4 kg，l1=0.8 m，l2=0.6 m，θ1=π/6 rad，θ2=π/3 rad，Δl=5 mm，Δl′=1 mm，θ˙1=2.4rad/s,θ˙2=1.8 rad/s, θ¨1=2.56rad/s2,θ¨2=3.14 rad/s2代入式（30）、式（31）,得τ与Δl、Δl′的表达式：

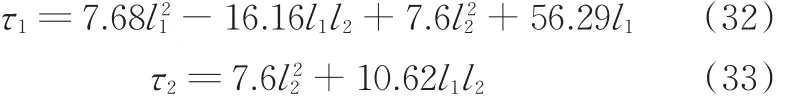
设l1、l2制造误差的范围分别为0.78～0.82 m，0.58～0.62 m，则可得l1、l2对关节1和2力矩误差的影响。

由图7可知，l1误差对τ1的最大误差由3.48 N·m减小为1.2 N·m，l2误差对τ1的最大误差由0.7 N·m减小为0.1 N·m；l2误差对τ2的最大误差由1.73 N·m减小为0.35 N·m，l1误差对τ2的最大误差由0.23 N·m减小为0.07 N·m。由此可知，通过基于瀑布机制的自组织模式可有效地减小误差的范围。

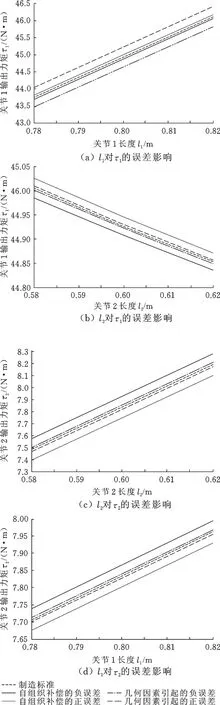
图7 关节误差对关节惯性力制造标准的影响趋势Fig.7 Influence of joint errors on the joint inertia force respectively

4 结论

（1）以高速、高精度的重载机械手为研究对象，从机械手的动力学方程出发，推导出机械手关节的惯性矩阵、重力项、哥氏力和离心力，进而求解机械手各关节的输出力矩。

（2）针对机械手运动中的关节误差对重载机械手末端精度的影响，受生物瀑布机制自动修复特点的启发，提出基于瀑布机制的重载机械手自组织精密模式。利用求解的自组织精密模式，对关节制造误差及转动误差对关节惯性力的影响进行分析，数值仿真分析表明：基于瀑布机制的重载机械手自组织精密模式能够有效地减小关节几何因素对重载机械手精度的影响。