SCARA机器人的自适应迭代学习轨迹跟踪控制

张 铁 李昌达 覃彬彬 刘晓刚

1.华南理工大学机械与汽车工程学院，广州，510000 2.桂林航天工业学院，桂林，541004

0 引言

机器人为完成作业，需要按照预期轨迹实现一定的位姿，但由于机器人动力学系统内部的不确定性以及各种外界干扰，导致机器人末端在多次运动后实际轨迹偏离期望轨迹甚至发散，从而无法进行正常作业，因此对机器人关节进行快速精确的轨迹跟踪控制十分重要。目前针对机器人轨迹跟踪的先进控制策略主要分为如下几大类：滑模变结构控制［1］、自适应控制［2］、神经网络控制［3］与迭代学习控制［4］，实际中采用的控制方法往往结合了上述多种控制策略。OUYANG等［5⁃6］针对机器人轨迹跟踪问题提出了一种PD滑模控制方法，它的控制效果相对于标准滑模控制有所改善；孙明轩等［7⁃8］提出的自适应重复学习控制方法能使轨迹误差随着循环次数的增加而减小，但是控制律含有许多待定参数；BINGÜL等［9］针对二自由度机器人轨迹跟踪问题提出的粒子群算法解决了机器人抖动的问题。上述方法存在减小轨迹误差效果不明显、计算复杂等不足。目前多数工业机器人通常用于重复运动工作，如喷涂、装配、焊接、搬运等，这些情况下机器人末端的轨迹是周期性的，而迭代学习控制（ILC）适合于运动具有重复性的对象的高精度控制，且能实现对轨迹的完全跟踪［10⁃12］，因此迭代学习控制方法较其他方法具有一定优势。但迭代学习方法的缺点是难以与其他控制方法相融合，这是因为经典迭代学习控制需要被控对象具有全局Lipschitz连续及严格相同初始条件两个前提［13］，因此有许多学者致力于研究新的理论体系，使迭代学习控制能与其他先进控制思想结合成崭新的体系［14］。

本文基于CHIEN等［15］提出的自适应迭代学习控制（adaptive iterative learning control,AILC）算法，将迭代学习控制理论与传统PD控制结合，并采用自适应控制的理论思想，利用误差信息来调节控制力矩，从而改善轨迹跟踪精度，提高系统的控制品质。

1 机器人动力学模型

目前，串联关节型机器人的机械结构均为伺服电机带动减速器运动，减速器输出轴与手臂连接，SCARA机器人同样具有这一结构形式。本文使用SCARA机器人来验证自适应迭代学习控制算法的有效性，提高机器人轨迹跟踪控制的精度。实验平台采用AR4215型四轴SCARA机器人（图1）。利用表1所示的SCARA机器人的DH参数对该系统进行运动学建模，在每个轴上固定一个参考坐标系，如图2所示，其中，第一、二轴的连杆长度均为200 mm。

图1 SCARA机器人Fig.1 SCARA robot

表1 SCARA机器人的DH参数Tab.1 The DH parameter of SCARA robot

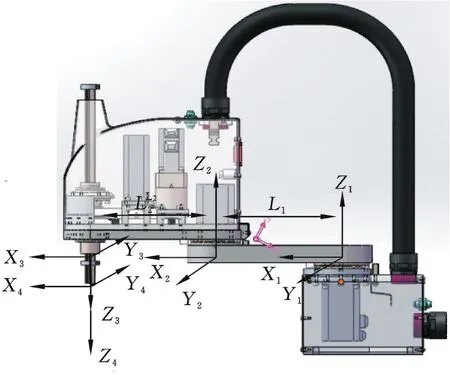
图2 SCARA机器人的运动学模型Fig.2 The kinematics model of SCARA robot

实验时仅将机器人的前三轴作为轨迹跟踪控制对象，根据拉格朗日方程得到其前三轴的动力学方程：

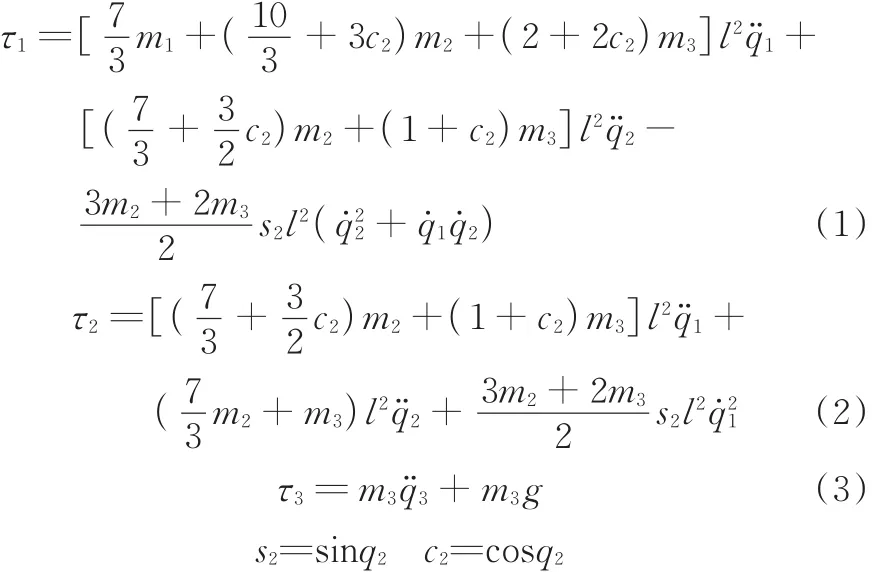
式中，τ1、τ2、τ3分别为关节 1、2、3 的力矩；m1、m2、m3分别为连杆1、2、3的质量；l为连杆1、2的长度；q1、q2、q3分别为连杆1、2的转角和连杆3的移动距离。

式（1）～式（3）可以写成统一形式：

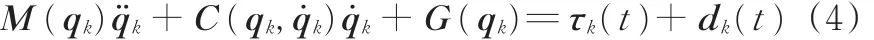
式中，t为时间，t∈[0,T]；下标 k∈Z+表示迭代次数；qk、q˙k、q¨k∈ R3分别为关节第 k次运动时的广义位移、广义速度和广义加速度；M(qk)∈R3×3为机器人的惯性矩阵；C(qk,q˙k)q˙k∈ R3为离心力和科氏力；G(qk)∈ R3为重力项；τk(t)∈R3为输入控制力矩；dk(t)∈R3为外界干扰项与摩擦力项的总和。

本文的目标是针对该机器人动力系统设计一个控制律，使得当k→∞时，qk收敛于对应时刻的[0,T]，其中，跟踪误差 ek=qd-qk,e˙k=q˙d-q˙k。

假设系统精确参数未知且满足如下条件：

（1）∀t∈ [0,T]，期望轨迹 qd、q˙d、q¨d及干扰 d均有界；

（2）初 始 值 满 足 q˙d0-q˙k0=qd0-qk0=0,∀k∈ Z+；

再假设系统满足一般n轴串联机器人模型且具有如下特性：

（3）M(qk)∈Rn×n为对称正定且有界的矩阵；

（4）M˙(qk)-2C(qk,q˙k)为对称矩阵，且满足xT(M˙(qk)-2C(qk,q˙k))x=0,∀x ∈ Rn；

（5） ||M(qk)q¨d-dk|| ≤ β,||C(qk,q˙k)||≤kc||q˙k||,||G(qk)||＜ kg,∀t∈[0,T]，其中，参数 β、kc、kg为正实数。

2 自适应迭代学习控制算法

文献［15］针对多关节机器人系统提出了一种迭代学习控制方法，该方法在经典PD反馈控制的基础上，通过自适应迭代项克服机器人系统的未知参数和干扰带来的不确定性。下面给出该方法的具体内容以及收敛性分析。

针对以上问题描述，设计如下控制律：

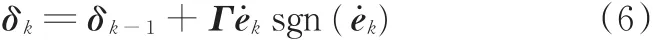
式中，δk为迭代项且是自变量t的函数，首项δ-1=0；KP、KD为 PID 参数，KP，KD∈Rn×n；Γ∈Rn×n为自适应律参数，sgn(e˙k)∈Rn表示对 e˙k中的每一个元素取符号后得到的向量。

由式（5）可以看出，控制力矩由三项组成，前两项为经典PD反馈项，第三项为迭代项，前两项的反馈力矩与第三项的前馈力矩共同作用来调节力矩。第三项中的系数δk随迭代次数的改变而改变，且每次改变都是基于上次迭代系数与本次轨迹误差而进行的，体现出该算法“学习”的特征；算法中并未出现与机器人动力学系统有关的项，所需要的仅仅是每次迭代时的位置误差和速度误差信息。该算法如图3所示。

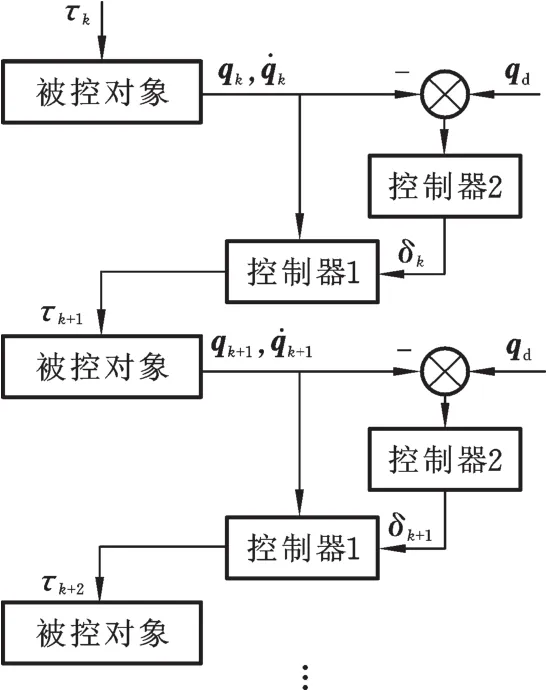
图3 算法结构图Fig.3 The structure chart of algorithm

对跟踪误差的收敛性的证明过程［15］分为三个部分：第一部分提出了系统的Lyapunov函数序列Wk，并证明该序列是单调递减的；第二部分证明上述序列的首项有界，由Wk的非负性可知整个序列均为有界函数；第三部分证明在迭代次数趋于无穷时，跟踪误差趋于零。

2.1 证明Wk的递减性

取如下的Lyapunov函数：

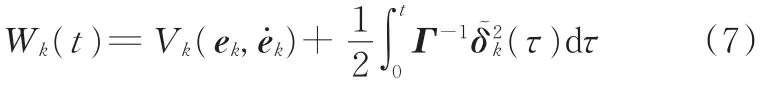
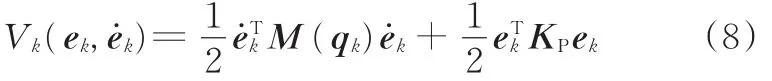
对式（8）两边同时求导，然后在区间[0,t]上进行积分可得

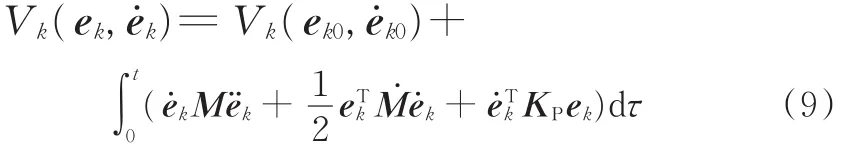
由于 ek0=e˙k0=0，因此式（9）中 Vk(ek,e˙k)=0，将式（4）与假设（4）中的满足条件代入式（9）可得

将（5）代入式（10）可得

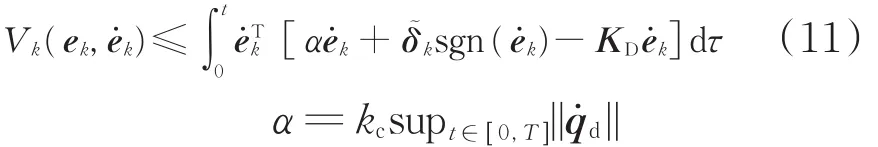
为了证明ΔWk≤0，有

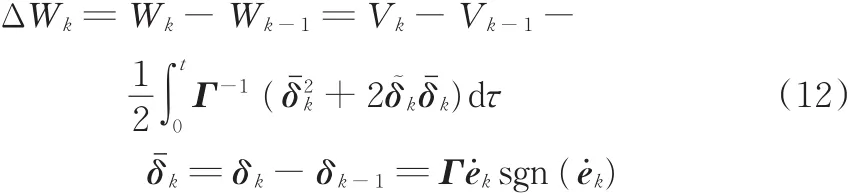
用式（11）中的Vk(ek,e˙k)替换式（12）中的Vk，

可得

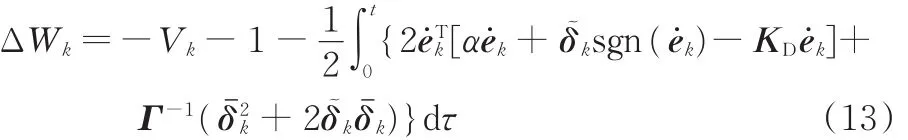
再 将 δˉk= δk- δk-1= Γe˙ksgn(e˙k) 和 δ~=δ-δk代入式（13）并化简即可得

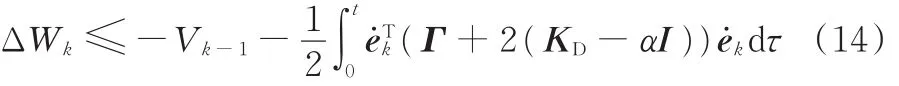
在式（14）等号右边，由于Vk-1非负，因此只需保证2(KD-αI)为正定矩阵，则可说明ΔWk非正，即Wk是非增序列。若能进一步证明W0有界，则可以说明整个Wk序列都是有界的。

2.2 证明W0的有界性

取k=0，对式（7）左右两边求导可得

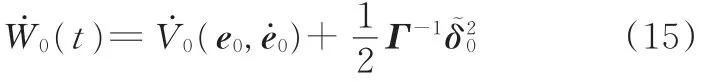
将式（11）中积分符号内的式子代入式（15）可得

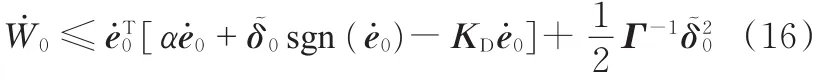
将 δ~0= δ - δ0，δ0= Γe˙ksgn(e˙k)代入式（16）并化简可得

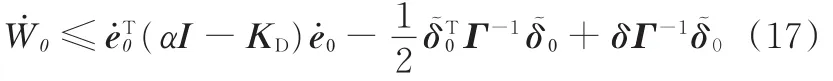
对于式（14）中的第三项，由基本不等式可得

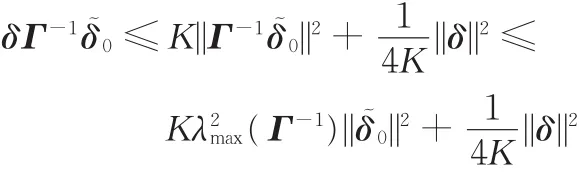
因此

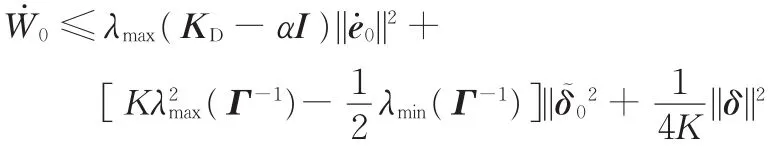
式中，λmax、λmin分别为矩阵A的最大特征值和最小特征值。

由于初始给定的值都有界，故 ||e˙0||、||δ~0||都有界，因而W˙0(t)有界，这意味着W0在[0,T]上一致连续有界，所以整个Wk序列都是有界的，进而可知ek、e˙k对于任意k ∈ Z+都有界。

2.3 证明 ek、e˙k 的收敛性

为推导ek、e˙k的收敛性，将上述 Lyapunov函数Wk改写为

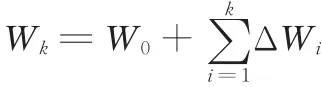
将式（11）代入上式可得

将上式进行移项化简可得

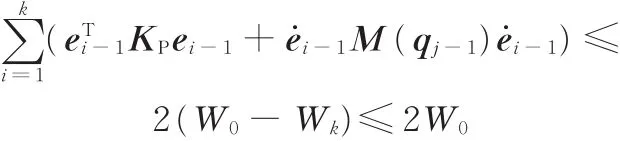
根据以上分析，最终可以得到

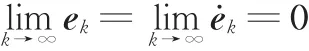
此外，注意到式（5）中虽然含有符号函数，但不会引起机器人的颤振现象，因为

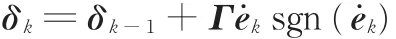
不妨将δk写成如下形式

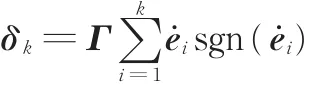
由于在轨迹跟踪过程中，qi本身偏离期望值qd不是很远，因此可以认为∀i=1,2,…,k,ek≈ed，这时

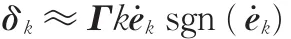
控制器（式（5））中含有符号函数的项为

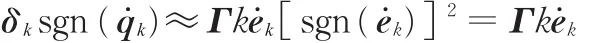
在上述近似中，符号函数被约去，并不会造成力矩值的突变。

上述证明从理论上推导出了“在迭代次数k趋于∞时轨迹误差趋于0”的结论，下面通过SCARA机器人的轨迹运动实验来验证该结论的正确性。

3 实验及结果分析

实验平台采用的SCARA机器人的工业控制系统架构是x86，机器人第一、二轴为转动轴，减速比分别为50∶1和80∶1；第三轴为移动轴，均采用交流伺服电机驱动。利用其前三轴的轨迹跟踪运动对上述自适应迭代学习控制算法（式（5）、式（6））的有效性进行验证，并将其与PD型迭代学习控制算法τk+1=τk+KPq+KDq˙进行对比。

在机器人运行的实验过程中，实时采集机器人各关节电机的编码器读数，通过Ethercat总线通信协议和实时操作系统保存到上位机，进行实验数据分析。

实验分为两个部分，第一部分规划SCARA机器人第三轴末端的期望轨迹为空间中两点P1、P2之间的一条线段，如图4a所示；取运动时间为0.76 s，控制器参数为KP=KD=5.0，Γ=［10 0.2 5］T，记 SCARA 机器人从 P1运动至 P2再返回P1为一次迭代过程。第二部分规划SCARA机器人第二轴末端的期望轨迹为平面中两点Q1、Q2之间的一条圆弧，如图4b所示。取运动时间为4.59 s，控制器参数与直线轨迹实验相同，记SCARA机器人从Q1以圆弧轨迹运动至Q2，再以直线返回Q1为一次迭代过程。机器人的首次运动可以得到轨迹误差信息，将误差代入式（5）、式（6）便可以得到第一次迭代过程的迭代系数与补偿力矩，将其发送至控制器用于控制机器人的第二次运动。重复上述迭代过程得到每次的误差数据。

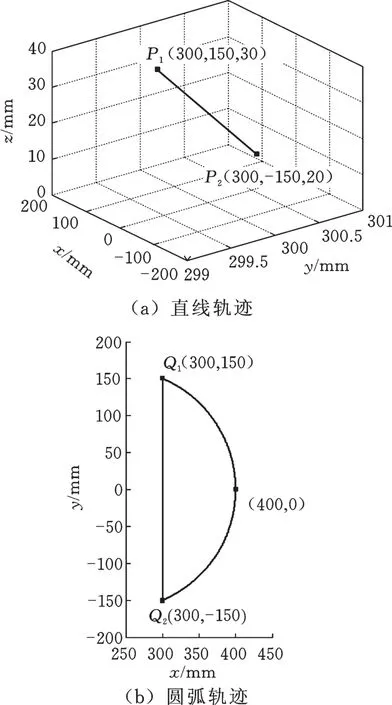
图4 SCARA机器人末端期望轨迹Fig.4 The desired trajectory of SCARA robot end

将文中提出的AILC算法用于SCARA机器人，得到的直线轨迹运动实验误差曲线如图5所示，图6给出了采用AILC算法与PD型ILC算法的直线轨迹最大误差，可以看出，随着迭代次数的增大，3个轴的误差都呈递减趋势，且AILC算法的误差收敛速度较PD型ILC算法快，经过10次迭代后，三轴误差均有较大程度降低，具体数据如表2所示；3个轴的误差曲线大致为中心对称图形，这是由于机器人的运动轨迹为路径相同的来回直线；前两轴的曲线较第三轴光滑，是因为前两轴减速器使用的是谐波减速器，其摩擦力矩小且波动均匀，而第三轴直接由电机经过多级齿轮系减速器和同步带传递到滚珠丝杠实现直线运动，而齿轮系减速器传递运动中存在摩擦力不均匀问题，因此跟踪误差曲线存在一定的抖动现象。

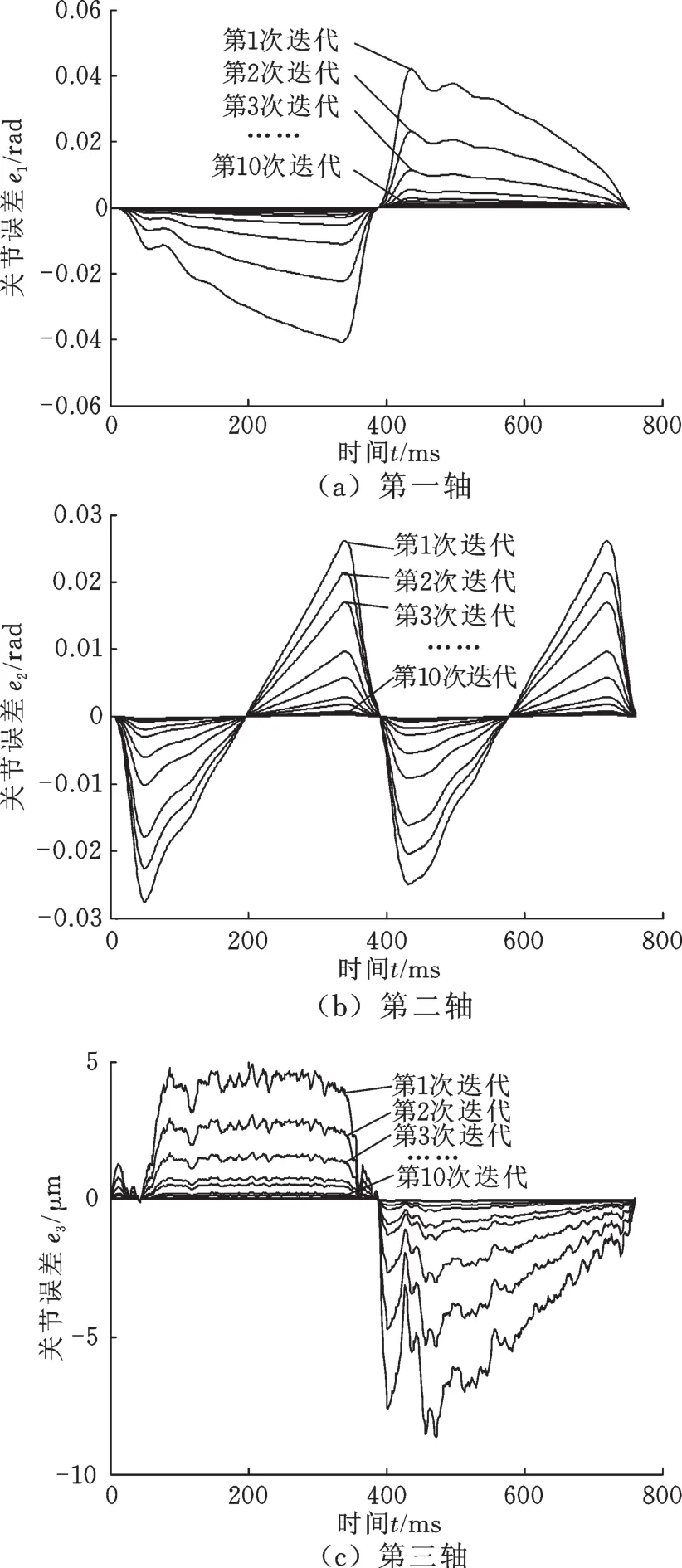
图5 SCARA机器人直线轨迹运动各轴误差变化情况Fig.5 The linear trajectory error for each axis of SCARA robot

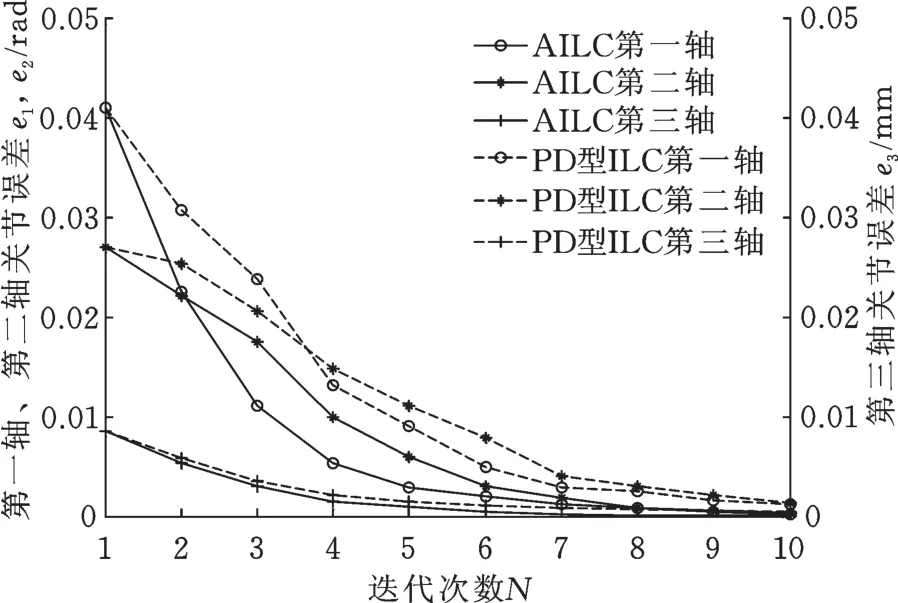
图6 直线轨迹最大误差随迭代变化情况Fig.6 The change of the linear trajectory maximum error with iteration

表2 直线轨迹误差数据Tab.2 The data of linear trajectory error

采用AILC算法的SCARA机器人圆弧轨迹运动实验误差曲线如图7所示，图8给出了分别采用AILC算法与PD型ILC算法的圆弧轨迹最大误差，可知，AILC算法的收敛速度略快于PD型ILC算法，但收敛速度较直线轨迹要慢，这是由于圆弧运动具有向心加速度限制，运行速度要低于直线轨迹，因此初始较小，导致迭代效果较果较直线运动不明显，具体数据如表3所示。图7中，2 s处出现的误差突变对应轨迹的转角处Q2。实验结果说明：文中提出的自适应迭代学习控制算法可以很好地完成轨迹跟踪任务，随着迭代次数的增加，可以将轨迹误差减小至一定范围内，且对于初始误差较大的情况具有更好的跟踪效果。

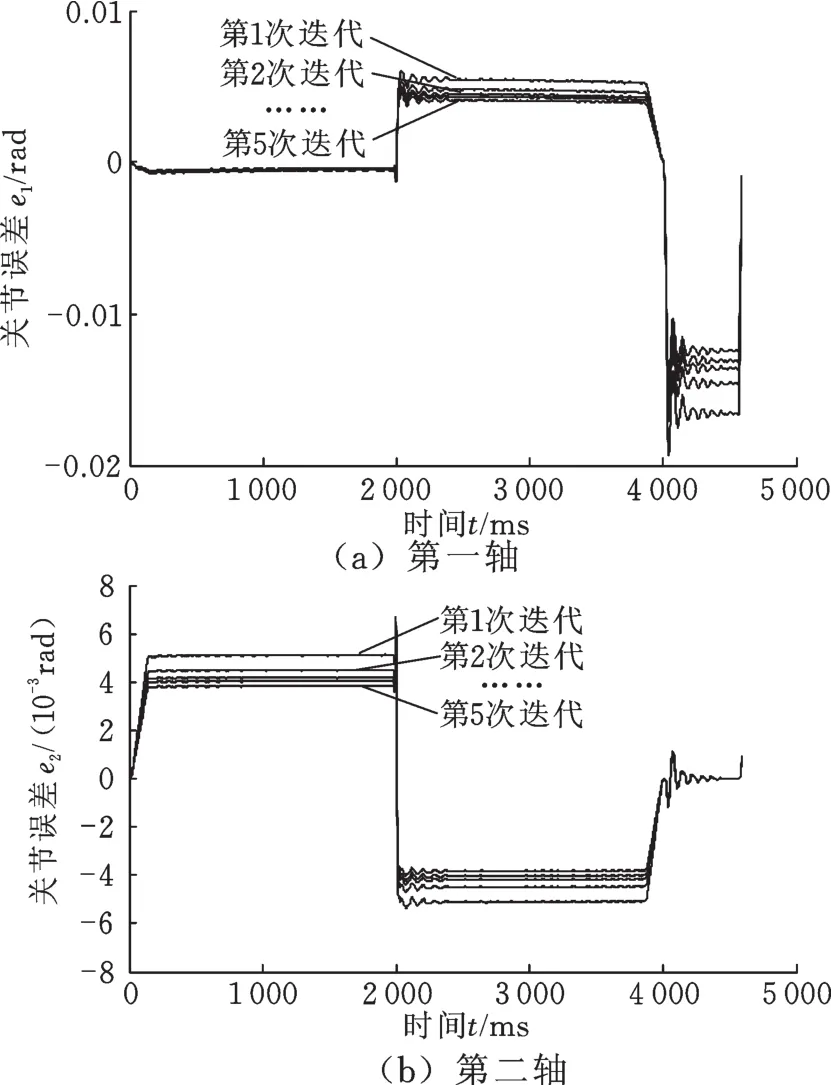
图7 SCARA机器人圆弧轨迹运动各轴误差变化Fig.7 The arc trajectory error for each axis of SCARA robot

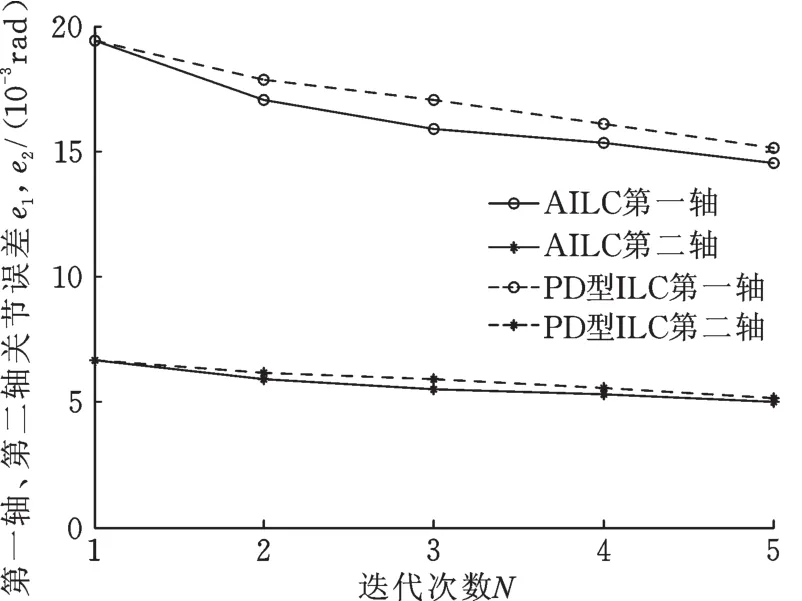
图8 圆弧轨迹迭代过程中最大误差变化过程Fig.8 The change of the arc trajectory maximum error with iteration

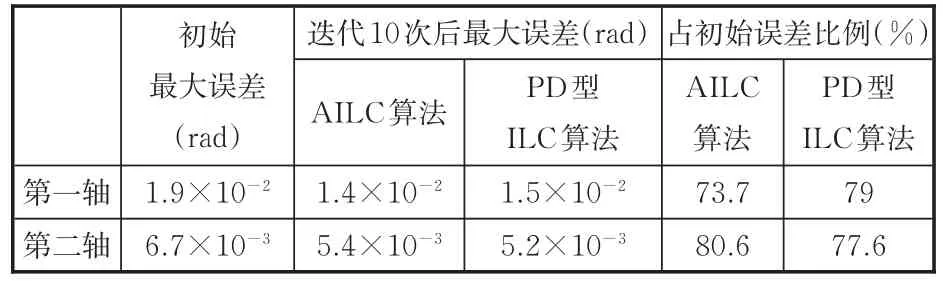
表3 圆弧轨迹误差数据Tab.3 The data of arc trajectory error

4 结论

为了减小执行重复运动任务的四轴SCARA工业机器人的末端轨迹位置误差，在CHIEN等［15］提出的自适应迭代学习控制算法的基础上进行了更深入的研究。首先利用SCARA机器人的拉格朗日方程和构造的Lyapunov函数序列，从理论上证明了轨迹跟踪误差的收敛性，并说明其能够避免颤振现象；搭建了一个四轴SCARA机器人实时轨迹跟踪控制实验平台，构建了基于Ethercat的总线系统，算法的计算结果通过前馈力矩输出到SCARA机器人驱动器，实现了轨迹跟踪控制；结合机器人动力学模型及相关参数，将自适应迭代学习控制算法应用于SCARA机器人，直线运动轨迹和半圆弧运动轨迹的实验验证了该方法是可以用于工程控制的，且该方法使机器人直线轨迹实验中第一轴误差减小为初始误差的1.61%，提高了SCARA机器人的轨迹跟踪精度。