轴表面矩形微螺旋槽织构对唇形油封密封性能的影响

江华生 孟祥铠 彭旭东 李伟荣

1.嘉兴学院生物与化学工程学院，嘉兴，314001 2.浙江工业大学机械工程学院，杭州，310014 3.嘉兴学院机电工程学院，嘉兴，314001

0 引言

唇形油封由于结构简单、性能可靠和安装方便等优点广泛应用于各种工程机械中旋转轴的密封场合，其主要作用是阻止机壳内润滑油工作介质向外界泄漏。唇形油封的动密封原理是轴转动时唇口依靠其表面的粗糙微凸体或纹理的非对称周向弹性变形引起的流体反向泵送作用机制［1］，即将油封已泄漏到唇口空气侧的润滑油介质泵送回油侧的过程，其密切依赖的前提条件是油封唇口应具有非对称的几何结构和橡胶唇口表面存在大量的微观粗糙形貌［2⁃4］。

为了增强反向泵送作用以提升密封效果，人们在橡胶唇口或轴的表面设计及加工表面微织构，但是由于橡胶唇口的表面织构容易磨损而未得到更多应用［5］。随着金属表面激光加工技术的发展，在油封轴表面加工微织构增强反向泵送作用的研究越来越多。其表面微织构形式主要有两种：一种是离散型的表面微凹坑或微凸体织构，该种类的表面微织构在近十年研究较多［6⁃12］；另一种是连续型的表面微沟槽或微凸体。针对后一种类的表面微织构研究已成为近几年的热点。JIA等［13］对轴表面正弦曲线形状的微螺旋槽织构建立理论仿真模型，并采取有限体积法数值计算的方法，分析了微螺旋槽的角度、深度、密度和轴转速等参数对油封泵送率的变化规律，并与实验结果进行了对比；JIA等［14］、贾晓红等［15］随后又进一步对因不同加工方法而形成的轴表面微螺旋槽织构进行了理论与实验研究，结果表明微螺旋槽轴表面相对于光滑轴表面可以产生更高的油封泵送率，但是上述理论模型均假设油封唇口为光滑表面，忽略了实际存在的表面微观几何形貌产生的流体反向泵送作用；ELGADARI等［16］采用 JIA等［13⁃14］提出的轴表面微螺旋槽理论模型，假设唇口表面微观几何形貌为一维或二维的正弦函数分布形式，通过建立油封唇口瞬态的润滑理论模型并采用有限元法进行数值计算，研究了瞬态下不同微螺旋槽织构参数对油封泵送率的影响。

综上所述，本文基于油封反向泵送作用的动密封原理和弹性流体动压润滑理论，提出在唇形油封轴表面加工矩形截面的微螺旋槽织构，计入唇口表面微观粗糙形貌对密封界面流场分布的影响，建立油封唇口稳态的流体润滑理论模型，并考虑橡胶材料的固体弹性变形和流体液膜“空化”现象对唇口润滑的影响，采用有限元方法获得油封的泵送率、摩擦扭矩等密封性能参数，研究矩形微螺旋槽织构参数和轴转速对密封性能参数的影响规律。

1 理论模型

1.1 几何模型

唇形油封系统结构组成及轴表面矩形微螺旋槽分布示意图见图1。轴转动工作时，油封唇口尖端与轴表面之间形成沿轴向接触宽度b、基础膜厚h0的流体密封区，并通过轴表面矩形微螺旋槽的流体反向泵送作用实现更优异的密封效果，见图1a。轴表面微螺旋槽采用激光技术加工获得，螺旋槽沿轴表面周向间距λ均匀分布，螺旋角为α，槽深为hp。为便于计算分析，建立笛卡儿直角坐标系（图1b），其中，x、y分别代表轴表面的周向和轴向，轴表面速度U沿x方向，取周期性分布的矩形区域λ×b作为单元计算域。

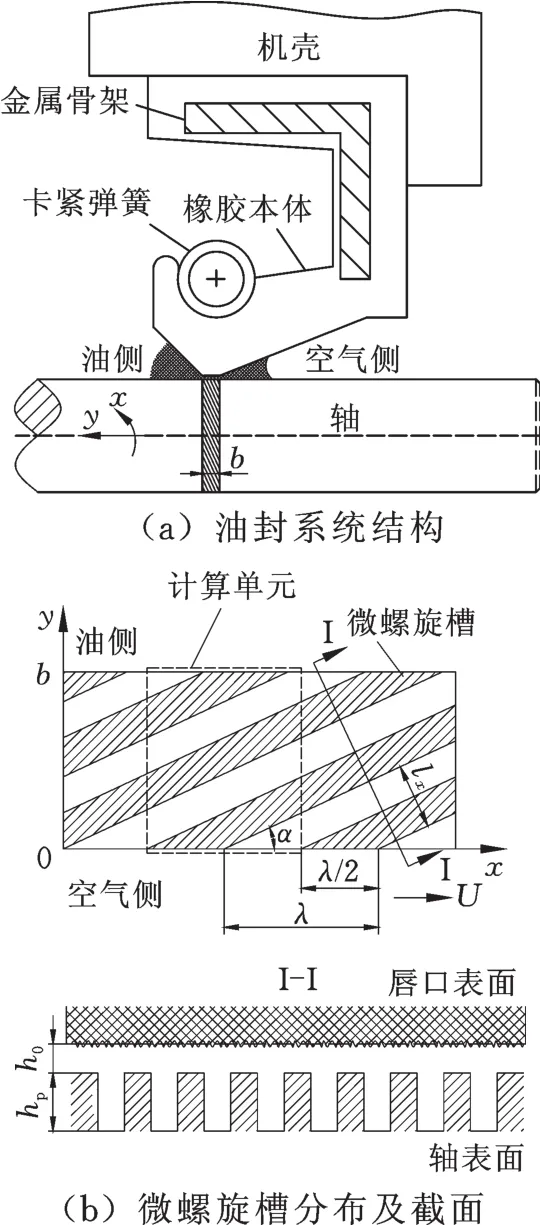
图1 油封结构组成及轴表面微螺旋槽分布Fig.1 Schematic diagram of lip seal and shaft surface micro-spiral grooves distribution

1.2 控制方程

当油封处于稳态工作状态时，唇口与轴表面的密封界面一般会形成稳定的流体动压润滑状态。假设油膜为牛顿性流体，流动状态为层流，忽略流体的挤压效应和惯性效应，油膜压力沿膜厚方向保持不变。基于以上假设，密封界面的流体压力分布可采用二维笛卡儿直角坐标系的不可压缩流体的雷诺方程描述［17］：式中，h为计算域内任意一点的油膜厚度；p为流体压力；μ为润滑油的黏度；ρ为流体密度。

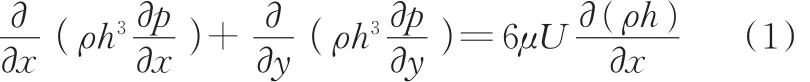
对于计算域的液膜区，由于ρ为常数（ρ=ρL，ρL为润滑油密度），故式（1）可简写成

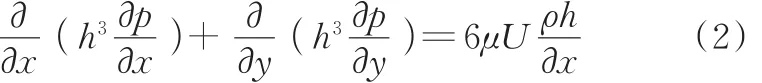
对于计算域的空化区，由于p为常数，且流体密度ρ=ρc（ρc为空化区油膜密度，且0＜ρc＜ρL），故式（1）可简写成

为便于编程计算，引入密度比系数θ=ρ/ρL，将式（2）和式（3）相统一，可得到等效的p-θ形式的控制方程［18］：

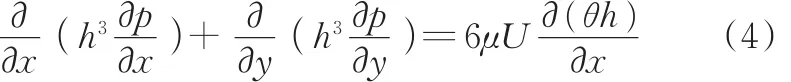
为求解式（4），对单元计算域施加下列相应的边界条件：

（1）JFO（Jakobsson-Floberg-Olsson）空化边界条件：

（2）强制性边界条件：

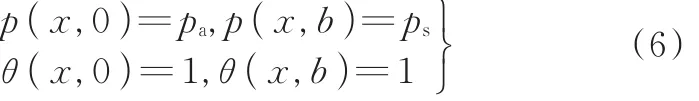
（3）周期性边界条件：

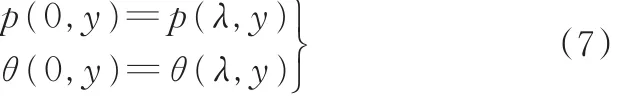
式中，pc为空化压力；ps为油侧压力；pa为空气侧压力。

1.3 膜厚方程

单元计算域内油膜厚度h（x，y）由初始基础膜厚 h0、唇口表面粗糙度函数 h1（x，y）、轴表面微槽织构函数h2（x，y）以及唇口表面弹性变形δ（x，y）等叠加而成，即

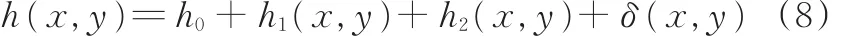
唇口表面在轴表面的摩擦作用下形成类似粗糙峰的微观几何形貌，粗糙峰的形状与分布采用二维的正弦函数描述［19］（图2），即

式中，A为粗糙峰幅值；λx、λy分别为粗糙峰沿周向和轴向的波长。

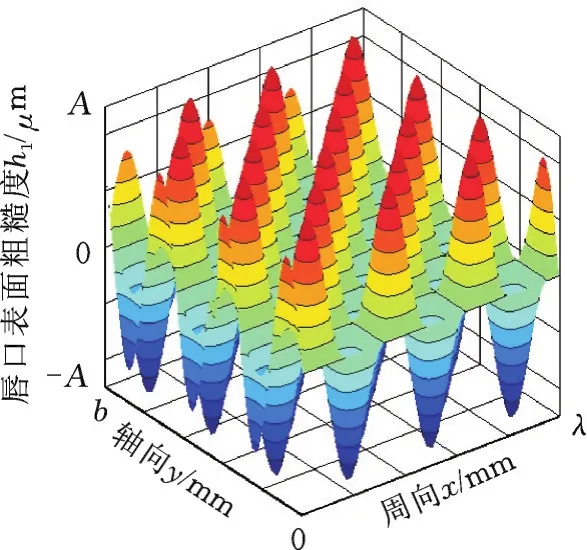
图2 油封唇口表面微观几何形貌3D分布图Fig.2 There”dimensional plot of lip seal surface roughness

设置轴表面矩形微螺旋槽的槽宽与槽间距相等，采用正弦函数描述矩形微槽的分布（图3），即

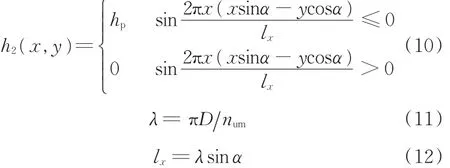
式中，D为轴的直径；num为微螺旋槽沿轴表面周向分布的线数；lx为微螺旋槽的法向间距。

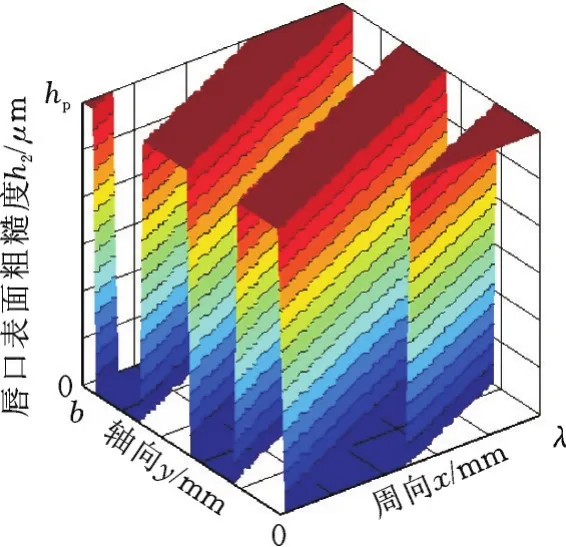
图3 轴表面微螺旋槽织构3D分布图Fig.3 There-dimensional plot of shaft surface micro-spiral grooves

唇口表面粗糙峰在流体压力p（x，y）的作用下发生弹性变形，从而使油膜厚度发生变化。单元计算域内任意节点的弹性变形δ（x，y），在数值上等于域内所有节点压力p（x′，y′）在该节点产生的变形之和，本文采用弹性体半无限体空间的Boussinesq［19⁃20］公式进行计算，即

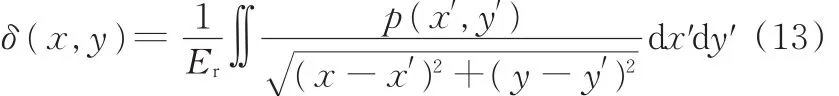
其中，Er为两接触面的综合弹性模量［21］，计算公式为

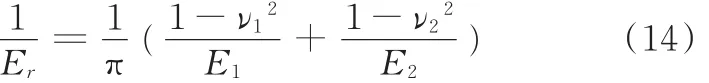
式中，E1、E2分别为钢与橡胶材料的弹性模量；ν1、ν2分别为钢与橡胶材料的泊松比。

1.4 黏温方程

油封工作时，轴转速是影响唇口密封界面流体温升的主要因素，而温升将导致流体黏度的变化，从而间接影响唇口密封区流体压力的分布，最终导致油封密封性能参数的变化，因此，润滑油黏度与温度的变化关系可变换为黏度与转速的关系。润滑油FAV3的黏度μ（pa·s）与轴（D=80 mm）转速n（r/min）的变化关系［15］如下：

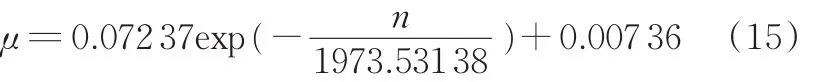
1.5 计算参数

为便于计算分析，选取油封工况、结构和材料等基本的计算参数见表1。需要指出的是，在分析某单个参数对油封密封性能的影响时，其他参数一概保持不变。

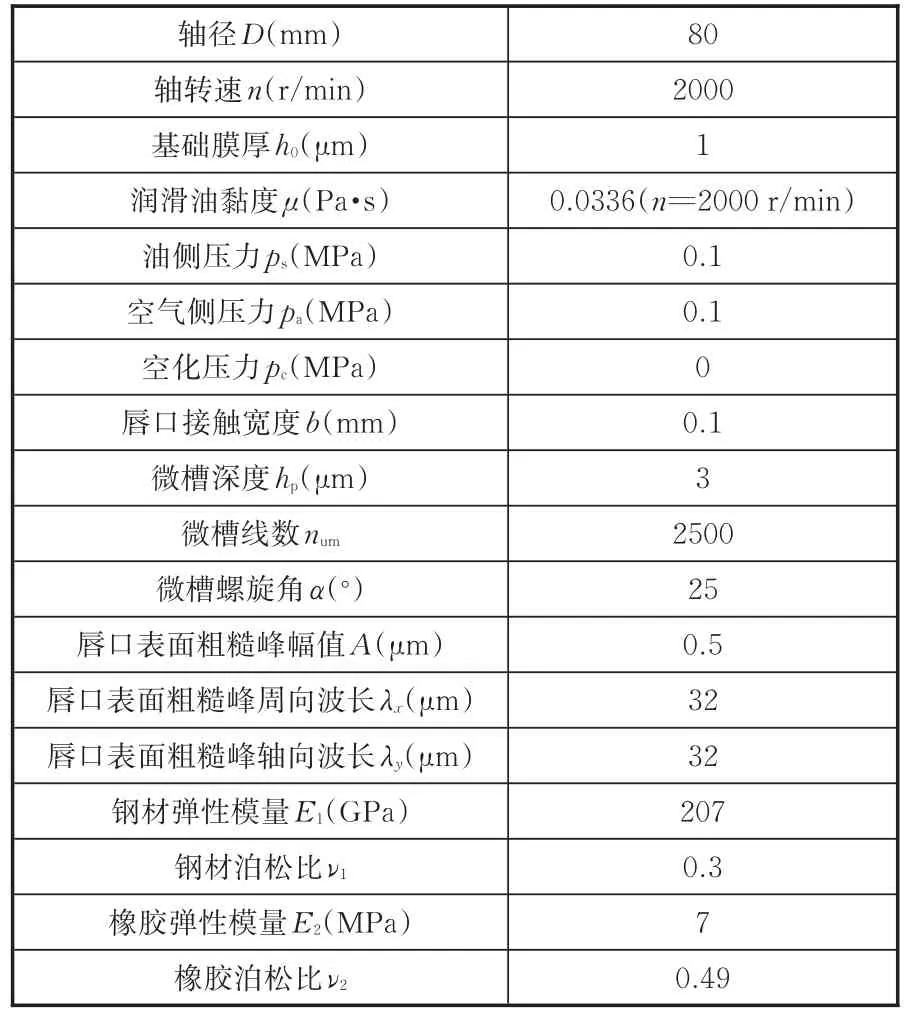
表1 基本计算参数Tab.1 Basic calculation parameters of lip seal

衡量唇形油封的密封性能参数主要有泵送率Q和摩擦扭矩T，其计算公式如下：

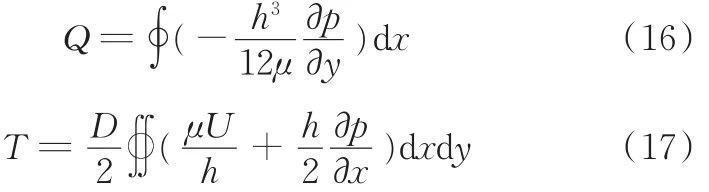
其中，Q是以无压力差唇形油封的空气侧边界计算得到的。

1.6 计算方法

由上述分析可知，油封唇口密封界面的流体压力与油膜厚度紧密相关，而唇口表面的弹性变形影响油膜厚度的大小，同时油膜压力又影响唇口表面的弹性变形，因此，油膜压力与唇口表面的弹性变形之间存在流-固耦合的关系。本文采用有限单元法离散控制式（4），联立弹性变形式（13）进行数值迭代的解耦计算，有限元网格节点数通过计算泵送率Q的网格数无关性检查后确定，计算程序流程见图4。其基本思路是：首先设定初始基础膜厚h0，采用有限元法计算流体压力p，收敛条件为式（5），流体压力p的具体计算方法见文献［22-23］；然后根据流体压力p计算弹性变形δ，根据式（8）更新膜厚h，并判断膜厚h是否收敛，若不收敛，采用超松弛迭代膜厚h后重新计算流体压力p，直至膜厚h前后两次的相对误差在允许范围内；最后根据流体压力p的计算结果，通过数值积分进一步计算得到泵送率Q和摩擦扭矩T，直至程序结束。

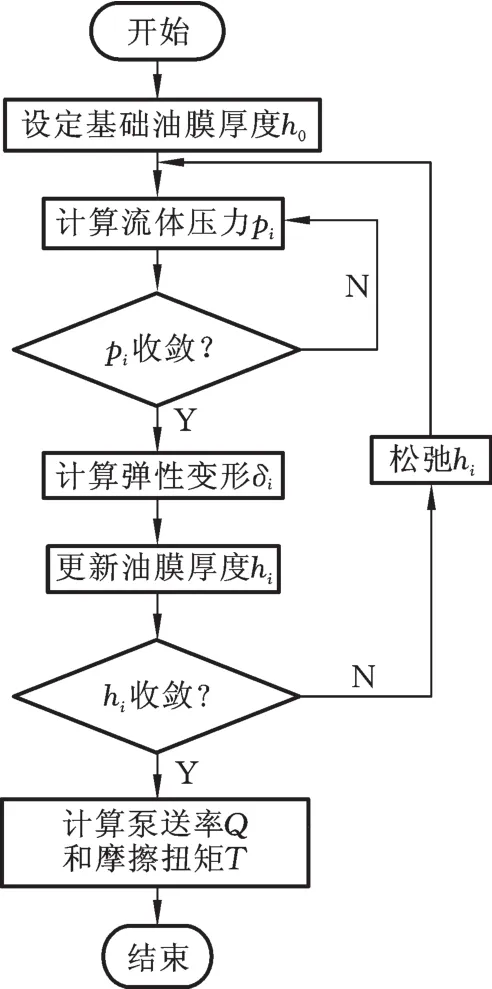
图4 数值计算流程Fig.4 Numerical calculation flow chart

2 计算结果及分析

2.1 计算域膜厚及流体压力分布

根据表1提供的基本参数进行计算得到的膜厚及流体压力分布结果见图5。其中，单元计算域的油膜初始厚度分布图见图5a，轴表面对应矩形微槽区域的油膜厚度大，反之则小，图中最大和最小油膜厚度分别为5.9µm和1.4µm；单元计算域流体压力分布的计算结果见图5b，从图中可知，对应油膜厚度大的矩形微槽区域形成的流体压力最小并且发生了“空化”现象，而两个矩形微槽之间的区域由于油膜厚度的突然变小而产生了较大的流体压力分布。由图5可知，流体压力分布与膜厚分布具有对应的流体动力学关系，说明油封唇口密封界面因轴表面的矩形微槽而产生了流体动压效应。

2.2 微螺旋槽织构参数的影响

（1）螺旋角α。不同转速下密封性能参数随矩形微槽螺旋角α的变化关系见图6。从图6a可知，随着螺旋角α的增大，泵送率Q先逐渐增大，当α=25°时，Q达到最大值，然后Q逐渐减小，其原因是随着螺旋角的变化，微槽对油膜流体的轴向导流能力发生变化；从图6b可知，摩擦扭矩T随螺旋角α的增大呈近似线性减小，这是因为随着α的增大，螺旋槽对油封唇口流体的周向导流能力增强，从而提高了轴表面的流体润滑性能。因此，为了获得较大的泵送率以提升密封效果，轴表面加工矩形微槽的最佳螺旋角约25°。

图5 计算域初始膜厚及流体压力的分布Fig.5 Pressure and initial film thickness distribution of a calculation cell

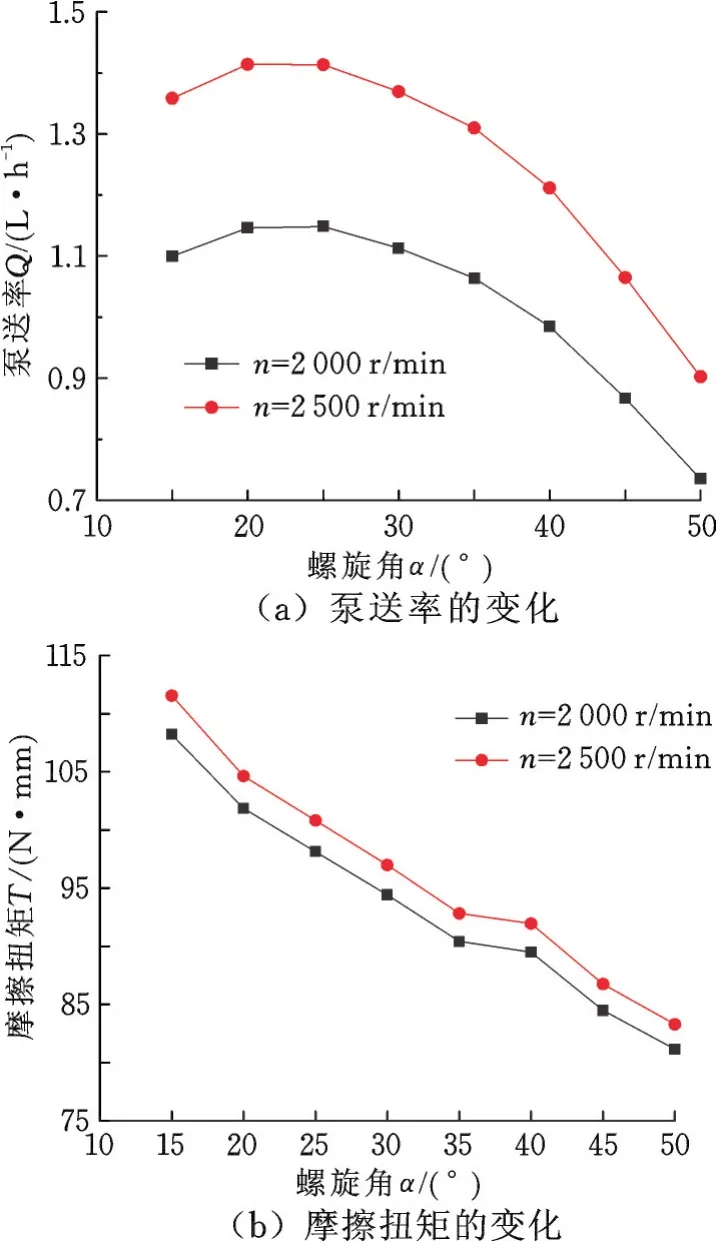
图6 密封性能参数随微槽螺旋角的变化Fig.6 Variation of lip seal performance with different micro-groove angles

（2）槽深hp。不同转速下密封性能参数随矩形微槽深度hp的变化关系见图7。从图7a可知，随着槽深hp的增大，泵送率Q逐渐增大且增幅越来越大，这是因为在油封工况参数不变的情况下，槽深越大，矩形微槽泵送的油膜体积流率就越大；从图7b可知，摩擦扭矩T随槽深hp的增大而逐渐减小，其原因是在槽深较大时，油膜厚度较大，则流体黏性剪切产生的摩擦力减小，导致流体摩擦扭矩降低。因此，在方便轴表面激光加工的前提下，增大矩形微槽的深度同时有利于提高泵送率和减小摩擦扭矩。

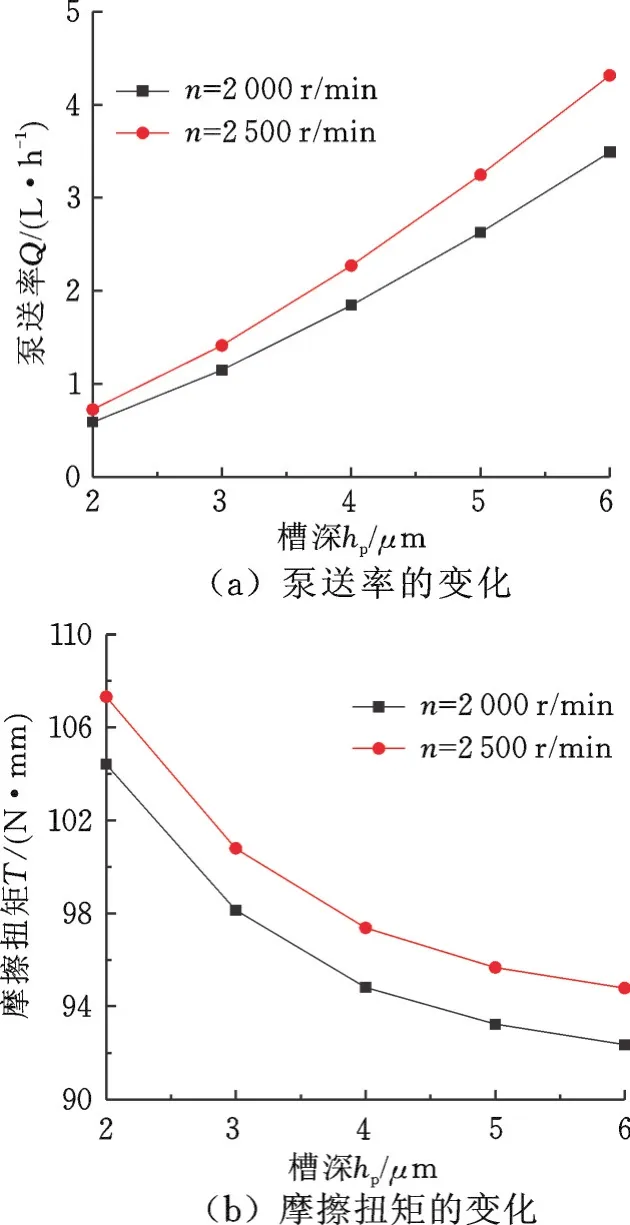
图7 密封性能参数随微槽深度的变化Fig.7 Variation of lip seal performance with different micro-groove depth

（3）线数num。不同转速下密封性能参数随矩形微槽线数num的变化关系见图8。从图8a可知，随着微槽线数num的增大，泵送率Q缓慢增大，其原因是随着微槽线数的增大，微槽单元的周向尺寸变小，导致微槽单元的泵送率降低，但因为轴表面微槽数量的增大，油封泵送率总体上表现出增大的趋势，这一变化规律与文献［13-14］相似；从图8b可知，摩擦扭矩T随微槽线数num的增大而呈现近似线性增大的变化趋势，因为轴表面微槽数量越多，相当于轴表面粗糙度越大，所以轴表面产生的流体摩擦力越大。因此，综合考虑微槽线数num对油封密封性能的影响以及方便加工的因素，轴表面矩形微槽线数num的取值应适中。

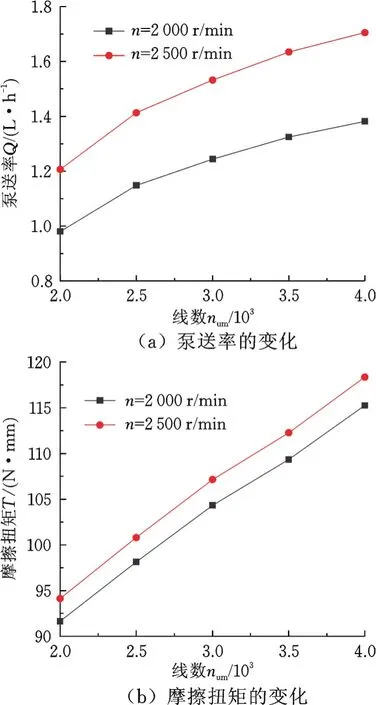
图8 密封性能参数随微槽线数的变化Fig.8 Variation of lip seal performance with different micro-groove numbers

2.3 轴转速的影响

对于轴表面矩形微槽织构参数一定的油封，转速n是影响无压力差油封密封性能的主要因素，密封性能参数随转速n的变化关系见图9。从图9可知，随着转速n的增大，泵送率Q呈近似线性增大的变化趋势；而摩擦扭矩T随转速n的增大呈先逐渐增大后缓慢减小，直至保持变化平缓的规律。其原因是，由于速度的不断增大，唇口密封界面的周向黏性剪切流相应增加，油膜的流体动压效应不断增强，促使矩形微槽对流体的轴向导流能力提高。因此，对于高速工况的油封，通过在轴表面设置矩形微螺旋槽织构更有利于提高泵送作用，从而实现工程机械旋转轴高速工况的密封。

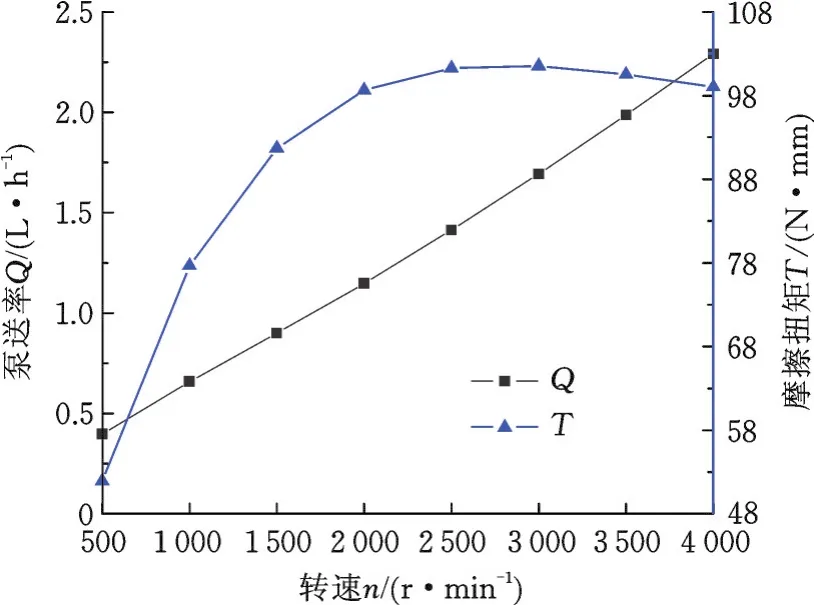
图9 密封性能参数随轴转速的变化Fig.9 Variation of lip seal performance with different shaft rotating speed

3 结论

（1）轴表面矩形微螺旋槽织构具有对油封密封界面液膜的反向泵送作用，因其改变了密封界面的流场特性，进而调控油封的泵送率和摩擦扭矩等密封性能参数，故将成为提升油封密封性能的一种重要技术手段。

（2）综合考虑油封唇口表面粗糙度、橡胶弹性变形，以及液膜空化、黏温变化对密封界面的影响，建立的数值计算模型可以分析预测流体润滑状态下轴表面矩形微螺旋槽织构参数对密封性能的影响。

（3）通过数值计算分析得到矩形微槽螺旋角α的最佳值约25°；较大的微槽深度可以同时提高泵送率和减小摩擦扭矩；增大微槽线数虽然可以提高泵送率，但同时也增大了摩擦扭矩，所以线数的取值以适中为宜；提高轴的转速，矩形微螺旋槽的泵送率相应增大。

(4)由于本文建立的微槽织构理论润滑模型基于油封密封界面处于稳态的完全液膜润滑状态，故对处于全工况下运行的油封密封性能分析具有一定的局限性。因此，今后可开展实验研究，并与数值计算结果相比较，从而进一步完善理论模型。