用不变本征算符法求晶面吸附原子的振动模∗
张科1)2)3) 范承玉1)† 范洪义2)
1)(中国科学院安徽光学精密机械研究所,中国科学院大气光学重点实验室,合肥 230031)2)(中国科学技术大学研究生院科学岛分院,合肥 230031)3)(淮南师范学院电子工程学院,淮南 232038)(2018年3月17日收到;2018年5月20日收到修改稿)
1 引 言
固体物理学主要研究固体的物理性质、微观结构、固体中各种粒子运动形态和规律以及晶体的振动模[1].从理论体系来看,包括微观理论与宏观理论:一方面在原子、分子水平上运用经典理论和量子理论研究固体表面的组成,原子结构及输运现象、电子结构与运动及其对表面宏观性质的影响等;另一方面在宏观尺度上,从能量的角度研究一系列的表面与界面现象,在实验的基础上建立对应的基本方程[2,3].近年来,由于各种功能器件的发展,促进了关于半导体陶瓷等各种功能材料表面与界面的研究;又由于各种新型复合材料的发展,对表面与界面的研究提出了新的课题.因此,关于各种材料表面与界面物理、化学性质的研究,已成为当前高科技尖端科学领域中的重要组成部分,是一个急待开发的方向[4,5].
表面物理与界面物理学的一个基本问题是晶体表面吸附一个原子以后晶格振动的变化情况[6].晶格振动是指晶体中的原子在做集体振动,其振动的频率对应于系统的能级差(能带).由于晶体原子间的相互作用,原子的振动不是孤立的,且晶格具有周期性,并以波的形式在晶体中传播,形成所谓的格波.一个格波表示晶体所有原子都参与的频率相同的(简谐)振动,常称为一种振动模.晶体振动模的研究一直受到国内外学者的广泛关注.中国科学技术大学基础物理中心的蒋最敏等[7]利用解动力学矩阵的方法计算了硅(111)面不同层数体系的所有表面振动模.福州大学物理系的洪水力[8]根据分子晶体的特征,应用空间群商群与点群同形原理,并配合结构分析方法,直接对RbC8H5O4晶体中的内振动模按不可约表示相容关系进行对称性分类.华中理工大学物理系安忠等[9]从计及了链间相互作用项的Su-Schrieffer-Heeger(SSH)模型出发,讨论了相邻两条链间电子跃迁对反式聚乙炔中孤子能谱及孤子附近的局域振动模的影响.浙江大学的李宏年等[10]对单层纳米碳管振动模的拉曼光谱进行了详细研究,测量了单层纳米碳管的一级、二级拉曼光谱,通过与理论值对照,对这些谱线做了初步标定.河北师范大学物理学院的谢尊等[11]基于扩展的二维SSH模型,研究了库仑钉扎作用对聚噻吩中双空穴极化子附近的局域振动模的影响.Jumeau等[12]对低密度聚乙烯中特定的自由基CH2的拉曼振动模式进行了详细研究,确定了不同的非晶和结晶拉曼匹配.晶格振动模的一般求解方法是以牛顿运动学方程为基础写出晶格的振动方程,而后根据周期性条件设其有行波解代入求解[13−15].但是,该方法在有表面杂质的情况下不适用,以至于在表面吸附位势系数β0与晶体内部周期位势系数β不同的情况下,晶体表面吸附一个质量为m0(与晶格原子质量m不同)的原子以后晶格的振动模一直未见文献报道.本文采用文献[16,17]中提出的不变本征算符方法,严格地推导出了这种吸附情形下晶体振动模的详细表达式,并讨论了振动模与吸附原子质量和晶体内位势的变化关系.本文所用方法简洁明了,无需涉及系统的具体量子态和波函数.
2 不变本征算符方法
不变本征算符[18,19](invariant eigen-operator,IEO)方法来源于量子力学的Schrödinger方程与Heisenberg方程的和谐[20,21].Schrdinger把和哈密顿算符H看成等价,因此在很多参考文献里被称为Schrödinger算子.Schrödinger方程为

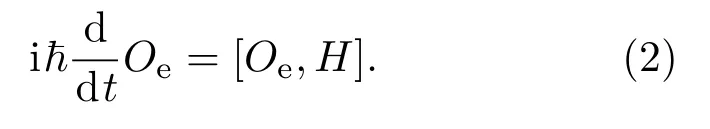

则有
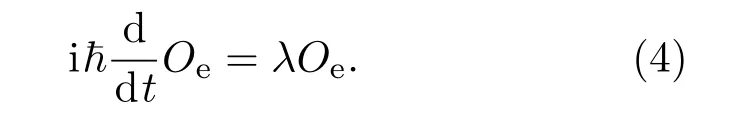
方程(4)可以看作是和能量本征态方程(1)“平行”的方程,换句话说,算符Oe在的作用下是“不变量”.这样,如果算符Oe满足(3)式,就称它为系统的一个“一阶”不变本征算符.在波函数的定态本征方程中,本征值E即代表系统的能量.而在引入的算符本征方程中,本征值λ与系统哈密顿量的本征能谱有密切关系,它对应的是系统的能级差.

再根据(3)式有

由于Oe是非零算符, 必然存在|ϕ〉a和|ϕ〉b使得a〈ϕ|Oe|ϕ〉b/=0,于是

即λ是系统的一个能级差.例如,一维谐振子的哈密顿量H1为

所以a就是一维谐振子的哈密顿量H1的“本征算符”,相应的本征值为ω,也是系统的能级差,这符合已知量子力学中的结果.
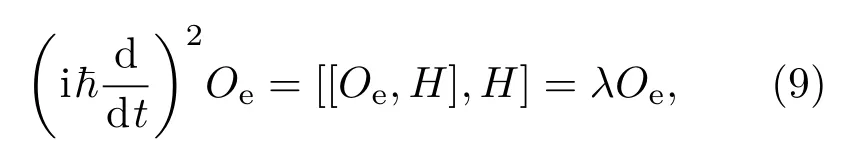
此时Oe称为“二阶”不变本征算符.由于对应于H2,所以就是两个相邻能级间的能隙.用类似于(6)式的证法可以说明这一点,即
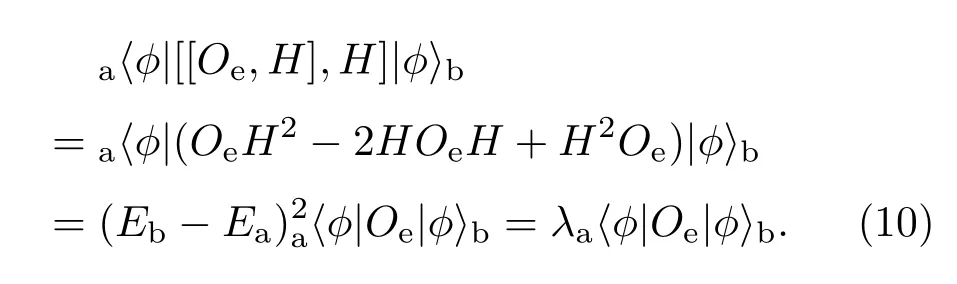
对一个系统的哈密顿量H,事先选定算符Oe作为这个系统的不变本征算符,按照(3)式从一阶开始做试探计算,若做一次对易子就有[Oe,H]= λOe,那么该体系的能隙就是λ,若做一次和二次都不满足算符方程,当做n次对易计算后有

借助IEO方法,充分利用海森伯方程,则无须涉及系统的具体量子态和波函数,就可以简捷方便地得到某些量子系统的能量本征值.对于固体物理中有复杂周期结构的哈密顿量,用IEO方法求系统的准粒子谱颇为有效.
3 吸附原子的晶面作为半无限原子链系统的振动模
图1所示是一个半无限原子链系统,一边无限延伸,另一边吸附一个原子,质量为m0,它不同于原子链中的原子质量m,只考虑相邻原子之间的相互作用,吸附原子的作用系数为β0,内部作用系数为β.
如图1所示,吸附原子后晶格的哈密顿量为[22,23]
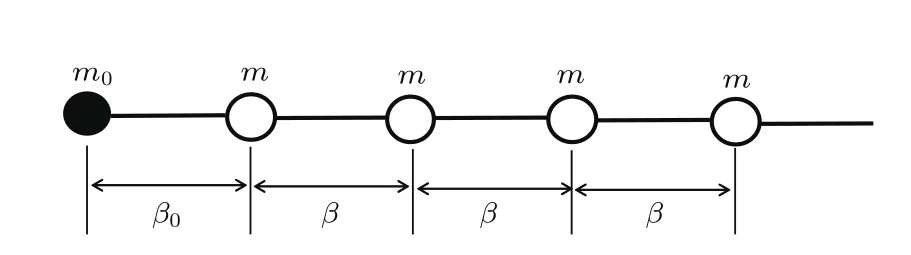
图1 吸附原子、吸附常数不同于晶体内部的半无限原子链模型Fig.1.The adatom and adsorption constant are different from those within the crystal of the semi-In finite atomic chain model.

其中P0是吸附原子的动量,Pn为其他原子的动量.
利用量子力学基本对易关系导出:

以及

设不变本证算符的形式为
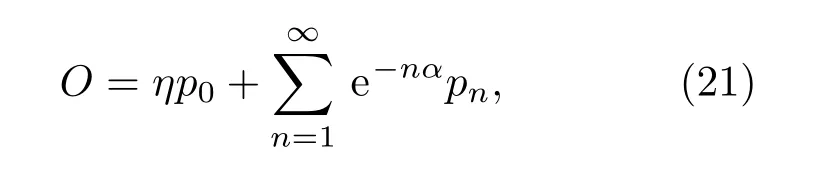
其中η,α为待定,代入本征算符方程得到

利用上述对易关系,(22)式化为

其中,
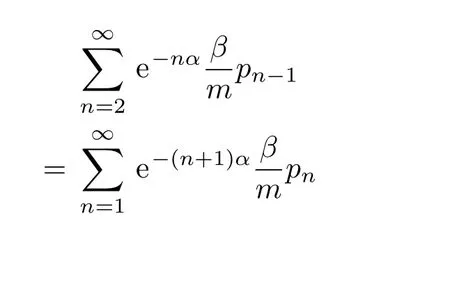
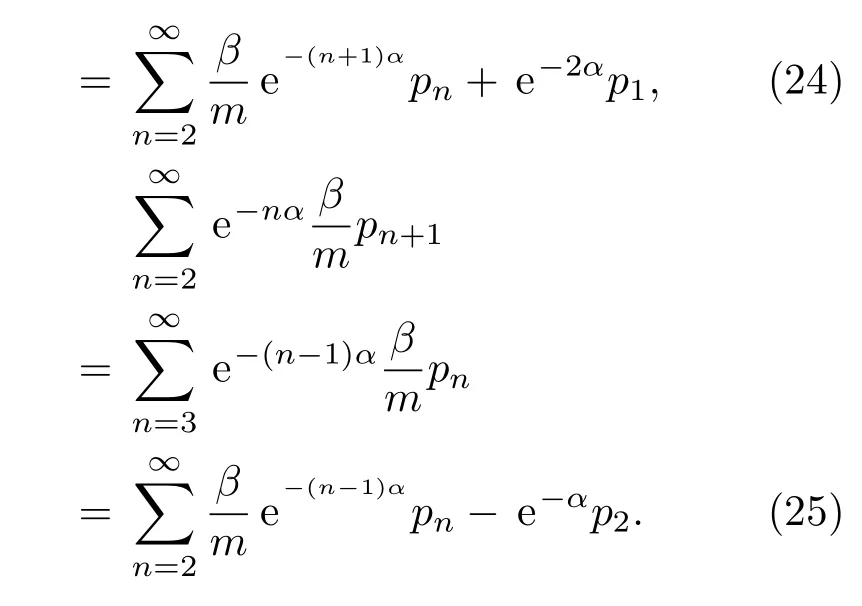
将(24)和(25)式代入(23)式得到:

比较本征算符的形式(21)式得到
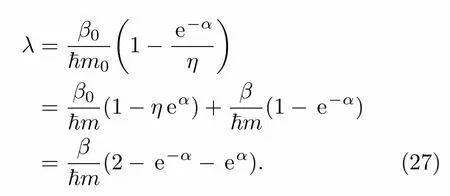
所以根据(10)式下的讨论可知,振动模式为
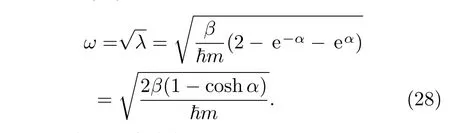
由(27)式可以连续求出:
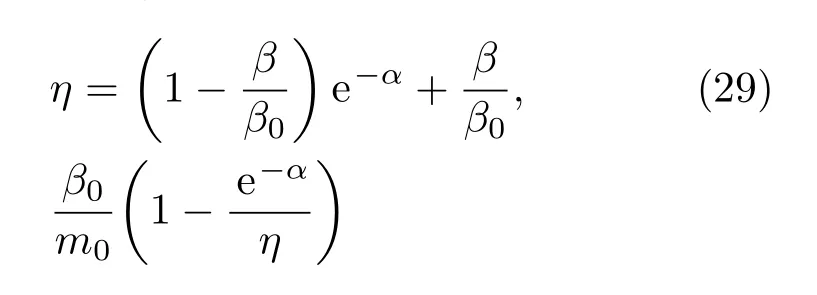
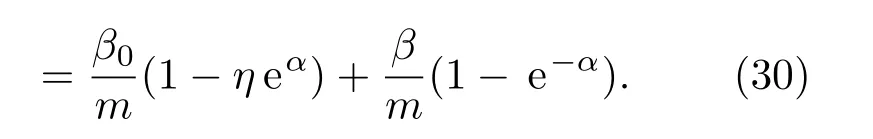
联立解方程(29)和(30)可得:

4 讨 论
1)当ħ=1,m/=m0,β = β0时,代入(32)式,得到

则系统的振动模式为

又由α0> 0得出

由于m和m0都是正数,上述不等式可以导出m>2m0,这就是形成稳定振动模的吸附条件.
2)当ħ=1,m=m0,β /= β0时,代入(32)式,得到

则系统的振动模式为

该结论与文献[13–15]的结果完全一致.
为了得出有意义的结果,有|eα|>1.再代入(36)式,得到

这是形成稳定振动模必须的吸附条件.
为了详细研究振动模ω与晶体内部原子的势常数β,晶格原子质量m、吸附原子质量m0的变化关系,我们分别绘出了相应的图形.
在图2中,设定β0=0.5,m0=1,做出了m=0.1,0.2,0.3,0.7四种情况下的晶格振动模ω与作用系数β的变化关系.从图中可以看出:1)在m0固定的情况下,ω随着β的增加而增加,在β趋向β0时ω趋向无穷大;2)对于相同的β值,m值越大,ω值越小.
在图3中,设定β0=0.5,β=0.1,做出了m0=0.1,0.2,0.3,0.7四种情况下的晶格振动模ω与晶格原子质量m的变化关系.从图中可以看出:1)当作用系数β,β0固定,ω随着m的增加而减小,最终趋于恒定值;2)衰减速度以及恒定值的大小随m0的增加而降低.

图2 晶格振动模ω随作用系数β的变化Fig.2.The relation between lattice vibration mode ω and the coefficient β.

图3 晶格的振动模ω随晶格原子质量m的关系Fig.3.The relation between lattice vibration mode ω and lattice atom mass m.

图4 晶格的振动模ω与吸附原子质量m0的关系Fig.4.The relation between lattice vibration mode ω and absorbing atom mass m0.
在图4中,设定β0=0.8,m=0.3,做出了m0=0.3,0.5,0.7,1.0四种情况下的晶格振动模ω与吸附原子质量m0的变化关系.从图中可以发现:1)当m,β0固定时,ω随着β的增加而增加,当β=β0时,趋向于无穷大;2)对于不同的m0值,在β0取较小值时,m0越小ω越大;随着β0的增大,m0越小ω越大.
5 结 论
采用不变本征算符方法严格推导出了晶体表面吸附一个质量为m0(与晶格原子质量m不同)的原子以后晶格的振动模,而且表面吸附势常数β0与晶体内部势常数β不同,严格地推导出了振动模的表达式,并分析了振动模ω与晶体内部原子的位势β,晶格原子质量m、吸附原子质量m0的变化关系.发现:1)在m0固定的情况下,ω随着β的增加而增加,在β趋向β0时ω趋向无穷大;2)对于相同的β值,m值越大,ω值越小;3)当作用系数β,β0固定,ω随着m的增加而减小,最终趋于恒定值;4)衰减速度以及恒定值的大小随m0的增加而降低;5)当m,β0固定时,ω随着β的增加而增加,当β=β0时,趋向于无穷大;6)对于不同的m0值,在β0取较小值时,m0越小ω越大;随着β0的增大,m0越小ω越大.

