钢弹簧浮置板轨道与隧道底板相互作用数值模拟

程 霖,杨成永,石永军,马文辉

(1.北京交通大学,北京 100044； 2.中铁六局集团有限公司,北京 100036)

地铁隧道中，无砟轨道与隧道底板并不是一个整体，轨道结构与隧道结构之间存在相互作用。当新建地铁线穿越既有线施工时，轨道结构与既有隧道底板之间将产生变形差异。当隧道底板变形较小时，两者的变形差异被测量误差所掩盖，当隧道底板变形较大时，两者的变形差异超过测量误差，严重时道床板与隧道底板将产生脱空。

人们已经注意到轨道与隧道结构变形不一致的现象[1，2]，但还未对轨道与隧道结构相互作用问题进行深入研究，因而在进行轨道结构力学分析时，大多将轨道与支承结构的变形视为等同[3，4]。现有研究表明，轨道与隧道结构产生变形差异的原因是：道床板在沉降槽内为钢轨所约束，导致其无法与隧道底板同步沉降，以至在隧道结构沉降较大时，道床板与隧道底板发生脱离。但这一说法有局限性，道床具有较大的刚度和自重，而钢轨的刚度相对较小，对道床的约束作用有限。

轨道结构与隧道结构脱空威胁到列车行车安全，轨道结构变形关系到新建线路施工方法的选择以及对轨道采取何种防护措施[5]。目前对既有隧道结构变形预测的研究较多[6-9]，但还未见能够预测轨道结构变形、轨道与隧道结构脱空的有效方法。因此，研究无砟轨道结构与隧道结构的相互作用具有重要意义。本文利用ANSYS建立考虑轨道与隧道相互作用的钢轨-钢弹簧浮置板道床-隧道底板有限元模型，计算隧道底板不同变形条件下轨道结构的变形和内力，较全面地认识无砟轨道结构与隧道结构相互作用的一般规律。

1 隧道底板变形方式

文献[1]提到，盾构隧道结构纵向刚度较小，能够与地层共同变形，而矿山法开挖的隧道结构纵向刚度大，当地层发生变形时，隧道结构呈整体的错台和转动。文献[6-7，10]通过对工程案例的对比分析，认为穿越工程造成的既有隧道结构沉降曲线近似正态分布，可用如下的Peck公式进行预测

式中，Smax为隧道底板最大变形值，位于变形曲线的中心(x=0)；i为沉降槽宽度，即变形曲线反弯点到中心的水平距离；S(x)为x处隧道底板的变形值。

综上所述，对于盾构隧道，本文采用Peck公式描述隧道底板变形，考虑下沉和上浮2种变形方式。对于矿山法隧道，考虑错台、向下折角和向上折角3种变形方式，如图1所示。

图1 矿山法隧道结构的3种变形方式

2 模型建立

2.1 计算假设

钢弹簧浮置板轨道用于城市轨道交通中对环境振动有严格要求的地段。轨道结构主要由钢轨、扣件、浮置板道床、钢弹簧隔振器等部件组成。相邻浮置板间设置剪力铰，剪力铰具有较大的径向刚度，使相邻浮置板在变形缝处不致发生竖向差异变形，避免钢轨受到过大剪力[11]。

用ANSYS软件按照图2所示的计算简图建立有限元模型。模型对实际结构进行了如下的简化：①扣件简化为弹簧，采用COMBIN14单元模拟；②钢轨视作由扣件弹簧间断支承在支承块上表面的长梁，采用BEAM188单元模拟；③浮置板厚度方向尺寸远小于其他两个方向的尺寸，简化为薄板[12]，采用SHELL181单元模拟；④钢弹簧隔振器简化为仅受压弹簧，采用LINK180单元模拟；⑤将2块浮置板变形缝处的竖向位移耦合，以模拟剪力铰的作用[13]。

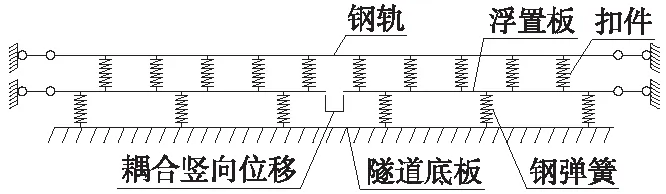
图2 钢弹簧浮置板轨道与隧道相互作用计算简图

2.2 计算参数

模型取足够的计算长度，对于盾构隧道，当隧道底板最大变形发生在浮置板中部时，模型取3块浮置板，总长为90 m；当隧道底板最大变形值发生在浮置板中间变形缝处时，模型取2块浮置板，总长为60 m。对于矿山法隧道，认为隧道结构变形缝与浮置板变形缝是对齐的，模型取4块浮置板，总长为120 m。不同情况浮置板的布置方式如图3所示。根据文献[14-15]对钢弹簧浮置板轨道参数的研究，取单块浮置板尺寸为3.3 m(宽)×30 m(长)×0.6 m(厚)，其余计算参数见表1。

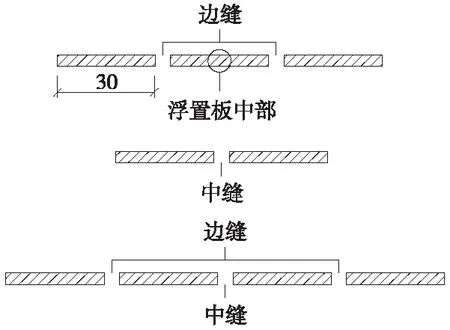
图3 浮置板道床布置示意(单位：m)

2.3 荷载及边界条件

约束钢轨两端的纵向(沿线路方向)自由度及钢轨所有节点的横向(垂直线路方向)自由度；约束浮置板两端的纵向自由度及侧边的横向自由度；约束隧道底板纵向和横向的自由度。

表1 计算参数

轨道结构有较大的自重，而钢弹簧的刚度相对较小，钢弹簧在轨道结构重力作用下产生的初始压缩量对轨道结构竖向位移的影响不可忽略，为此，计算时分为2个荷载步进行加载。第一步固定隧道底板，施加重力，使轨道结构在自身重力作用下产生位移。第二步在第一步基础上施加隧道底板位移荷载。轨道结构变形和内力提取第二个荷载步与第一个荷载步的差值，表示轨道结构仅在隧道底板位移作用下的变形情况。

3 计算方案及结果分析

3.1 计算方案

研究的物理量包括浮置板与钢轨的变形和内力，浮置板与隧道底板的脱空量和脱空范围。这里浮置板与隧道底板的脱空是指浮置板与隧道底板的差异沉降超过了钢弹簧的初始变形，钢弹簧不能承受拉力而与隧道底板脱离。

钢弹簧浮置板轨道与隧道结构相互作用的影响因素有：(1)隧道底板的变形方式；(2)隧道底板的最大变形值；(3)Peck沉降曲线中沉降槽宽度i的取值；(4)隧道底板最大变形值与浮置板变形缝的位置关系，也即隧道底板最大变形值发生在浮置板中部(以下简称“中部”)，或发生在浮置板中间变形缝处(以下简称“中缝”)。将计算方案列于表2。

表2 计算方案

3.2 计算结果

将所有工况的计算结果列于表3。

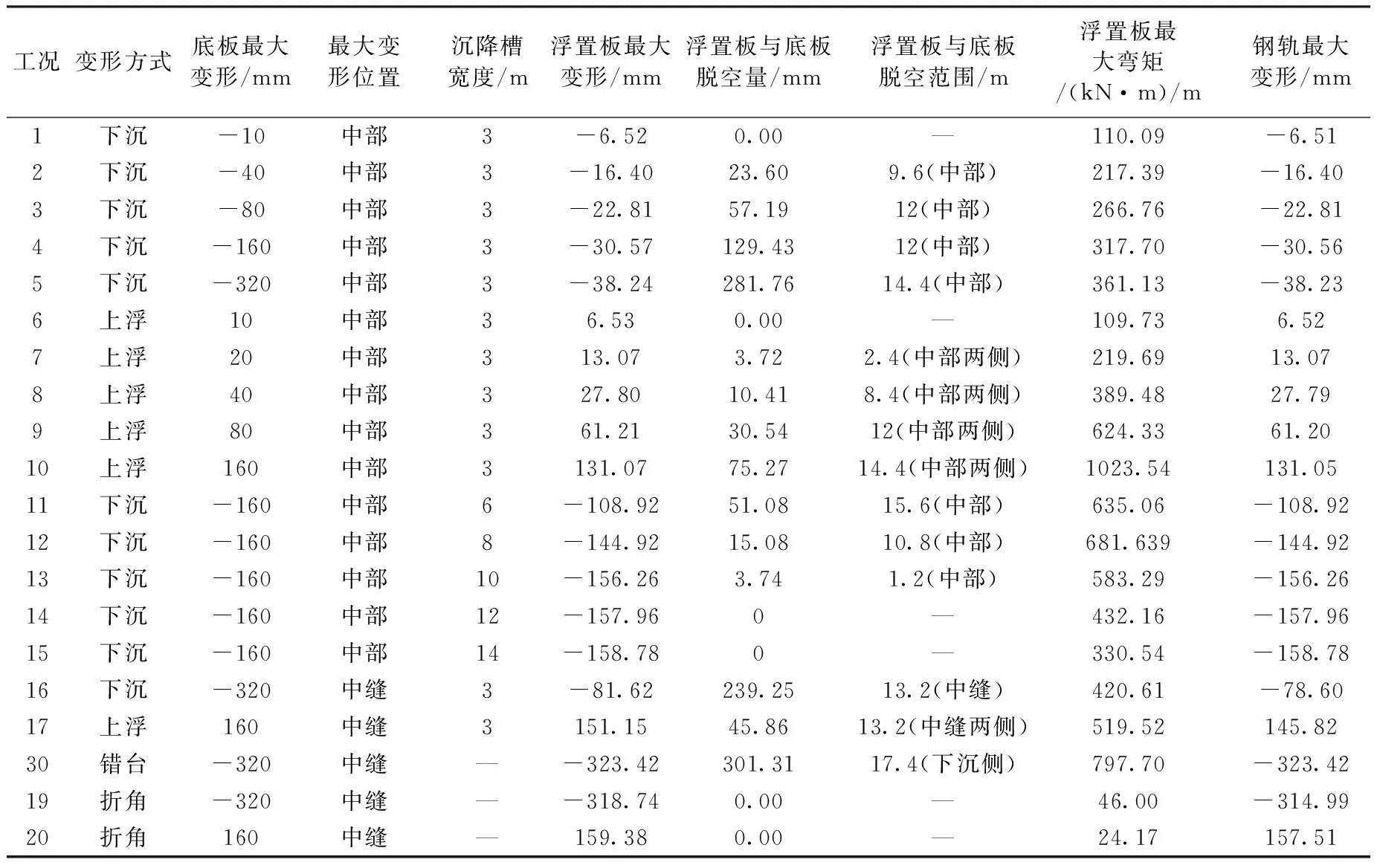
表3 计算结果

3.3 隧道底板变形方式的影响

(1)下沉的影响

以工况5为例，盾构隧道底板以Peck曲线形式下沉时，浮置板及钢轨的变形、弯矩如图4所示。可见盾构隧道结构发生沉降时，浮置板与钢轨的沉降小于下伏的隧道结构，在沉降槽内产生脱空。浮置板在沉降槽中心处产生弯矩最大值，在脱空区两侧产生较大的负弯矩。钢轨在浮置板变形缝处产生弯矩最大值，这是因为剪力铰不能抵抗弯矩，使钢轨在浮置板变形缝处产生弯折的结果。

图4 工况5计算结果

(2)上浮的影响

以工况10为例，盾构隧道底板以Peck曲线形式上浮时，浮置板及钢轨的变形、弯矩如图5所示。可见盾构隧道上浮时，浮置板在自身重力作用和钢轨约束下，最大上浮量比隧道底板小，且浮置板自身具有较大的刚度，在最大上浮位置两侧与隧道底板脱离。与下沉的影响类似，浮置板与钢轨的弯矩分别在最大上浮处和浮置板变形缝处达到最大。从数值上看，以工况4和工况10为例，最大下沉值与最大上浮值相同的情况下，上浮造成的浮置板与隧道底板的脱空量小于下沉，但浮置板与隧道底板的脱空范围、轨道结构的变形和内力均大于下沉。可见，其余条件相同的情况下，上浮对轨道结构的影响大于下沉。

图5 工况10计算结果

(3)错台的影响

图6 工况18计算结果

以工况18为例，矿山法隧道结构变形缝一侧发生整体下沉时，浮置板及钢轨的变形、弯矩如图6所示。可见在隧道底板整体下沉一侧，由于剪力铰和钢轨对浮置板竖向沉降的约束作用，浮置板与隧道底板产生了明显的脱空。钢轨与浮置板均在隧道底板整体下沉一侧产生了较大的弯矩，且钢轨弯矩在浮置板变形缝处产生突变达到最大值。

(4)折角的影响

以工况19为例，矿山法隧道结构发生向下折角时，浮置板及钢轨的变形、弯矩如图7所示，向上折角所得浮置板及钢轨的变形曲线、弯矩图与向下折角基本上关于横坐标轴对称。可见在隧道底板发生折角时，浮置板与隧道底板共同发生了刚体运动，未产生脱空。这是因为浮置板具有较大的自重和刚度，但钢轨刚度较小，对浮置板的约束作用不明显。从钢轨的弯矩图也可以看出，钢轨在浮置板变形缝处存在突变的弯矩值，而其余位置弯矩值约等于0，说明钢轨与浮置板和隧道底板的变形一致，这也反映了钢轨刚度较小，对浮置板的约束作用不大。

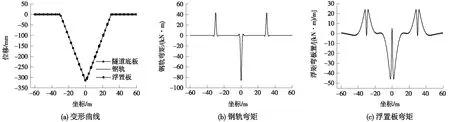
图7 工况19计算结果

3.4 隧道底板变形值的影响

由表3可以看出，随隧道底板变形值的增大，浮置板及钢轨的内力和变形值、浮置板与隧道底板的脱空量和脱空范围均增大。如图8所示，浮置板与隧道底板的脱开幅度(脱空量/隧道底板变形值)[1]随隧道底板变形值的增大而增大，最后趋于平缓，说明脱空区的浮置板能够以自身刚度承受自重产生的弯曲变形。

图8 脱开幅度与隧道底板变形值的关系

由表3可以看出，盾构隧道结构以Peck曲线方式下沉时，浮置板与隧道底板首先在沉降槽中心产生脱空，随底板沉降值的增大，脱空范围逐渐向两侧扩展。盾构隧道结构以Peck曲线方式上浮时，浮置板与隧道底板首先在最大上浮值两侧脱开，随底板上浮值的增大，脱空范围逐渐向最大上浮值及两侧扩展。矿山法隧道结构在变形缝一侧产生整体下沉时，浮置板与隧道底板在整体下沉一侧脱开，并随下沉值增大逐渐向整体下沉一侧扩展。

3.5 浮置板变形缝的影响

盾构隧道中，当隧道底板最大变形值位于浮置板变形缝处时，以工况16和工况17为例，钢轨与浮置板的位移曲线分别如图9、图10所示。

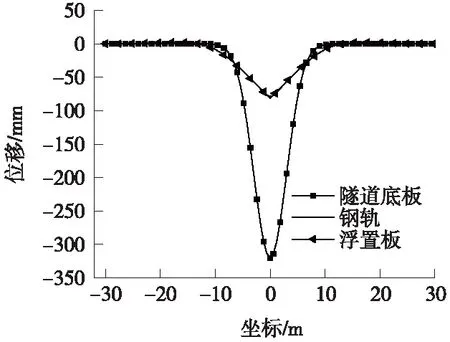
图9 工况16钢轨、浮置板、隧道底板变形曲线

图10 工况17钢轨、浮置板、隧道底板变形曲线

由此可见，当隧道底板最大变形值位于浮置板变形缝处时，浮置板和钢轨在沉降槽内发生明显的弯折。由表3可见，与最大沉降发生在浮置板中部相比，浮置板和钢轨的下沉量和内力有所增大，浮置板下沉量的增大使其与隧道底板的脱空量和脱空范围有所减小。与最大上浮发生在浮置板中部相比，浮置板与钢轨的上浮量和内力有所增大，浮置板与隧道底板的脱空量和脱空范围有所减小。这是因为浮置板变形缝降低了脱空区浮置板的整体性，浮置板较大的自重使其在脱空区范围内产生了较大的挠曲，减小了浮置板与隧道底板的变形差异。

3.6 沉降槽宽度的影响

通过工况4、工况11～工况15的计算结果可见，当沉降槽宽度i<10 m时，浮置板与隧道底板产生脱空；当沉降槽宽度i>10 m时，浮置板与隧道底板协同变形，不产生脱空。因此，当其余条件相同时，沉降槽宽度i越大，浮置板与隧道底板的沉降差异越小。

浮置板和钢轨弯矩最大值随沉降槽宽度i的变化曲线如图11所示。可见，浮置板与隧道底板脱开前，浮置板与钢轨的弯矩随沉降槽宽度i的减小而增大。浮置板与隧道底板脱开后，浮置板与钢轨的弯矩随沉降槽宽度i的减小而减小。这是因为浮置板与隧道底板脱开前，沉降槽宽度i的减小使浮置板和钢轨产生更大曲率的弯曲，进而弯矩增大，而浮置板与隧道底板脱开后，沉降槽宽度i的减小使脱空区跨度减小，相应的浮置板和钢轨的弯矩也减小。

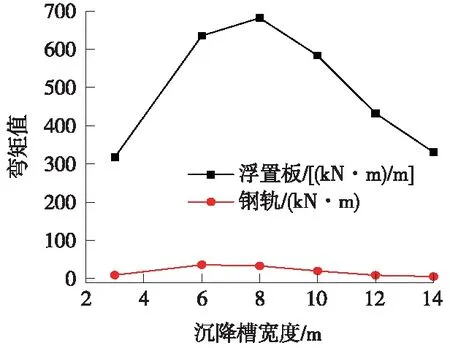
图11 轨道结构内力与沉降槽宽度的关系

4 结论

通过对有限元模型的计算分析可知，钢弹簧浮置板轨道与隧道结构相互作用有如下规律。

(1)轨道结构变形和内力、浮置板与隧道底板的脱空量及脱空范围均随隧道底板变形的增大而增大。

(2)浮置板与隧道底板产生脱空的主要原因是浮置板具有较大的刚度，而钢轨刚度较小，对浮置板起不到明显的约束作用。

(3)隧道底板最大变形发生在浮置板变形缝处时，与发生在浮置板中部相比，轨道结构内力和变形有所增大，但与隧道底板的差异变形减小。

(4)浮置板与隧道结构间的差异沉降随沉降槽宽度的减小而增大。轨道结构内力随沉降槽宽度的变化分为两个阶段：浮置板与隧道结构脱开前，轨道结构内力随沉降槽宽度的减小而增大；浮置板与隧道结构脱开后，轨道结构内力随沉降槽宽度的减小而减小。