基于损耗分离理论的非正弦激励磁心损耗计算方法研究

刘 任， 李 琳

(新能源电力系统国家重点实验室， 华北电力大学， 北京 102206)

1 引言

随着高压直流输电与电力电子技术的快速发展，具有高频损耗较低、饱和磁导率较高等优良特性的磁性材料(如超薄硅钢片、新型非晶及纳米晶合金等)在整流器、逆变器及高频变压器等电力电子装置中的应用越来越广泛[1，2]。然而，随着电力电子装置工作频率的提升，其内部磁心的功率损耗也会相应增高，由此而引发的工作性能下降、效率下降，以及制约高压直流输电技术发展等问题受到日益关注[3]。由于电力电子装置内部磁心通过的激励电压波形往往不是正弦波，而是三角波、方波等非正弦电压波形[4]，因此，提出一种精确且工程实用的非正弦激励磁心损耗计算方法，已成为电力电子装置内部磁心元件优化设计的首要任务。

从当前研究来看，磁心损耗的计算方法主要分为三类[5]：①基于材料物理特性的磁滞损耗模型[6]； ②基于经验的Steinmetz公式法[7]；③基于损耗统计理论的损耗分离法[8]。其中，磁滞模型主要有Preisach模型和Jiles-Atherton(J-A)模型。Preisach模型构建的基础是磁偶极子在时间与空间的统计特性，而J-A模型是基于磁畴壁的移动规律与宏观能量的平衡原理。虽然上述磁滞模型能较为准确地计算出磁心损耗，但该模型本身固有的复杂性造成了其模型参数的识别提取过程较繁琐，且计算量较大，尤其在非正弦激励工况下，难以满足磁心元件优化设计等领域对损耗模型提出的准确且实用的要求。

与磁滞模型形成鲜明对比，Steinmetz经验公式法具有简洁的损耗表达形式，且损耗系数只需通过实验数据拟合即可得到[9，10]。针对原始Steinmetz公式只适用于正弦激励的问题，后续提出了多种求解非正弦激励损耗的改进Steinmetz公式[10]。需要指出的是，Steinmetz经验公式法缺乏对磁性材料损耗产生机理的解释，因而其所适用的频率与磁感应强度范围较窄，且损耗计算的精度较低[11]。

Bertotti[12]为解决上述Steinmetz公式法过于依赖经验的问题，从磁性材料损耗产生的机理出发，提出了损耗分离理论，将损耗分解为磁滞损耗、涡流损耗和剩余损耗，并提出了相应的损耗计算公式，同时适用于正弦及非正弦激励波形。在Bertotti提出损耗分离理论之后，Amar[13]、Boglietti[14]和Barbiso[15]在该理论的基础上，分别提出了各自改进及扩展的非正弦激励下的磁心损耗算法，以此满足工程应用领域需准确快速求解磁心损耗的需求。虽然以上三位学者提出的损耗算法具有相似的理论基础，但其构建的损耗分离方程及模型参数的辨识方法却不尽相同，具有不同的求解精度和模型参数提取复杂度。

为此，本文以计算精度与模型参数提取复杂度为评价指标，对比分析了上述3种基于损耗分离理论的非正弦激励磁心损耗算法，以此筛选出其中综合性能最优的算法。首先，从傅里叶分解、利用时域及频域的观点求解损耗等方面，对比分析了3种损耗算法；其次，探讨了3种损耗算法模型参数提取的复杂程度，并对其进行了客观评价；最后，通过测量硅钢、非晶及纳米晶3种磁心在三角波及方波激励下的损耗，验证了3种损耗算法的精度。

2 非正弦激励下的磁心损耗计算方法

Bertotti[12,16]通过分析磁性材料损耗产生的微观机理，提出了损耗分离的概念，并依此将损耗按产生原因的不同划分为3部分：磁滞损耗、涡流损耗及剩余损耗。用公式表述为：

P=Ph+Pcl+Pex

(1)

式中，Ph、Pcl、Pex分别为磁滞损耗、涡流损耗和剩余损耗。其中，磁滞损耗与磁化频率无关，故也称之为静态损耗；而涡流损耗、剩余损耗均与磁化频率相关，称作动态损耗。

针对硅钢片等带状磁性材料，当叠片厚度小于电磁场在该材料中的趋肤深度时，Bertotti基于磁感应强度均匀分布的假设和磁畴结构的随机统计分布特性，推导了瞬态涡流损耗及剩余损耗的解析表达式，得到带状磁性材料的瞬态损耗密度表达式：

(2)

式中，Ph(t)、Pcl(t)、Pex(t)分别为磁滞损耗、涡流损耗及剩余损耗；d为叠片厚度；σ为电导率；B为磁感应强度；S为叠片截面积；G为无量纲系数(G=0.1375)；V0为表征磁体局部磁场统计分布特性的参数[16]。

2.1 Amar算法

Amar[13]以Bertotti损耗分离法为物理基础，通过引入傅里叶分解的思想和电压波形系数的概念，提出了一种简洁高效的磁心损耗计算方法。该算法将周期损耗W(f)表示为：

(3)

式中，f为激励频率；Wh、Wcl、Wex分别为一个周期的磁滞损耗、涡流损耗和剩余损耗，其中磁滞损耗Wh与激励频率f无关；P为功率损耗。

根据式(2)，可得周期涡流损耗Wcl与剩余损耗Wex的计算式分别为：

(4)

(5)

式中，T为激励周期。

在参考正弦激励下，周期磁心损耗计算式为：

(6)

式中，上标“sin”表示正弦激励；f0为参考正弦激励频率；Bm为磁感应强度峰值。

在保持磁感应强度峰值Bm不变的情况下，任意激励频率f1对应的正弦激励磁心损耗为：

(7)

为利用正弦激励下的损耗求解非正弦激励下的损耗，Amar基于傅里叶分解的思想，将非正弦电压波分解成各阶次正弦谐波，继而通过各阶次正弦谐波损耗叠加的方式求得磁心在非正弦激励下的损耗。虽然推导出的损耗表达式[13]较为复杂，但Amar通过引入电压波形系数Fc，得到了一个简化的非正弦激励磁心损耗计算式：

(8)

2.2 Boglietti算法

Boglietti[14]基于Steinmetz公式与Bertotti损耗分离法，并利用傅里叶分解的方法，提出了一种基于激励电压特征求解磁心损耗的算法。在正弦激励下，该算法认为磁滞损耗Ph可用Steinmetz方程表示，从而避免了Amar算法需测量静态磁滞回线的限制。磁滞损耗Ph表示为：

(9)

式中，a为磁滞损耗系数；x为Steinmetz系数。

涡流损耗Pcl与剩余损耗Pex则根据Bertotti损耗分离法中Pcl、Pex与频率、磁感应强度的关系得出，可分别表示为：

(10)

(11)

式中，b、e分别为涡流损耗系数和剩余损耗系数。

因此，正弦激励下的磁心损耗Psin可表示为：

(12)

为求解非正弦激励下的磁心损耗，Boglietti运用傅里叶变换将非正弦电压波分解成各次正弦谐波，由此基于各阶次谐波损耗叠加得到非正弦激励下的磁心损耗计算公式。Boglietti[14]认为剩余损耗Pex较小，利用涡流损耗计算式(10)即可同时考虑涡流损耗和剩余损耗，因此其将剩余损耗系数e置零，最终推导的非正弦激励磁心损耗计算式为：

(13)

式中

η=Uav/U1,av

(14)

χ=Urms/U1,rms

(15)

P1,h、P1,cl分别为电压基波对应的磁滞损耗和涡流损耗；B1,m为电压基波对应的磁感应强度峰值；Uav、U1,av分别为电压整流平均值和电压基波整流平均值；Urms、U1,rms分别为电压有效值和电压基波有效值。

因此可知，该算法待提取的参数为损耗系数a、b、x。该损耗系数可通过正弦激励下实测值与计算值之间的差值r取最小值而求得：

(16)

式中，n为实验采样点个数；Pmea为实测损耗值；Pcal为利用式(12)计算所得的损耗值。

2.3 Barbiso算法

Barbiso[15]在Bertotti损耗分离法的基础上，提出了适用于非正弦激励的磁心损耗时域扩展算法。该算法直接对瞬态损耗，即式(2)进行积分，从而将非正弦激励下磁心周期损耗表达为：

(17)

由式(17)可得正弦激励下的磁心损耗为：

(18)

从式(17)可知，该算法待提取的参数为磁滞损耗Wh和分布特性参数V0，仅与磁感应强度峰值Bm有关，而与激励波形及频率f无关，大小可通过(Wsin-Wcl)与f1/2之间的线性函数关系式提取(Wsin、Wcl分别为正弦激励下的总损耗实测值与涡流损耗计算值)。磁滞损耗Wh为该线性函数关系式在频率f为0时的函数值，而分布特性参数V0可通过线性函数关系式的斜率得出。因此，Barbiso算法避开了Amar算法需测取静态磁滞回线的难题，可直接基于上述线性关系提取磁滞损耗Wh。

显然，Barbiso算法辨识磁滞损耗Wh和分布特性参数V0至少需要2个频率下的损耗测量值。同时需要注意的是，当磁感应强度峰值Bm不同时，Wh和V0均需重新进行提取。

综上所述，3种算法的磁心损耗计算式及参数提取所需实验数据见表1。从表1中可以看出，3种算法在提取模型参数方面各有特点，复杂程度各不相同。其中，Amar算法需要通过测量磁心静态磁滞回线的办法求取磁滞损耗，故该过程较为繁琐；而Barbiso与Boglietti算法的参数提取过程则相对简单，均只需测量样品在正弦激励下的多个损耗值，因此这两种算法的模型参数提取复杂程度相当。

3 三角波与方波激励下的损耗公式推导

三角波与方波是电力电子装置内部磁心元件通过的典型非正弦电压激励波形[17]。为此，本文推导了它们在3种损耗算法下的具体表达式。

表1 3种磁心损耗算法对比Tab.1 Comparison of three magnetic cores losses algorithms

3.1 Amar算法

三角波与方波电压的波形系数分别为：

(19)

(20)

式中，Um为电压的幅值。

三角波与方波电压激励下的磁心损耗表达式分别为：

(21)

(22)

3.2 Boglietti算法

三角波激励及磁通波形如图1所示。三角波电压在一个周期内的表达式为：

(23)

图1 三角波激励及磁通波形Fig.1 Triangle wave and corresponding flux curve

对于三角波电压有：

(24)

(25)

Um=8fNSBm

(26)

式中，N为线圈匝数。

因此，三角波电压激励下的磁心损耗计算式为：

(27)

方波激励及磁通波形如图2所示。方波电压在一个周期内的表达式为：

(28)

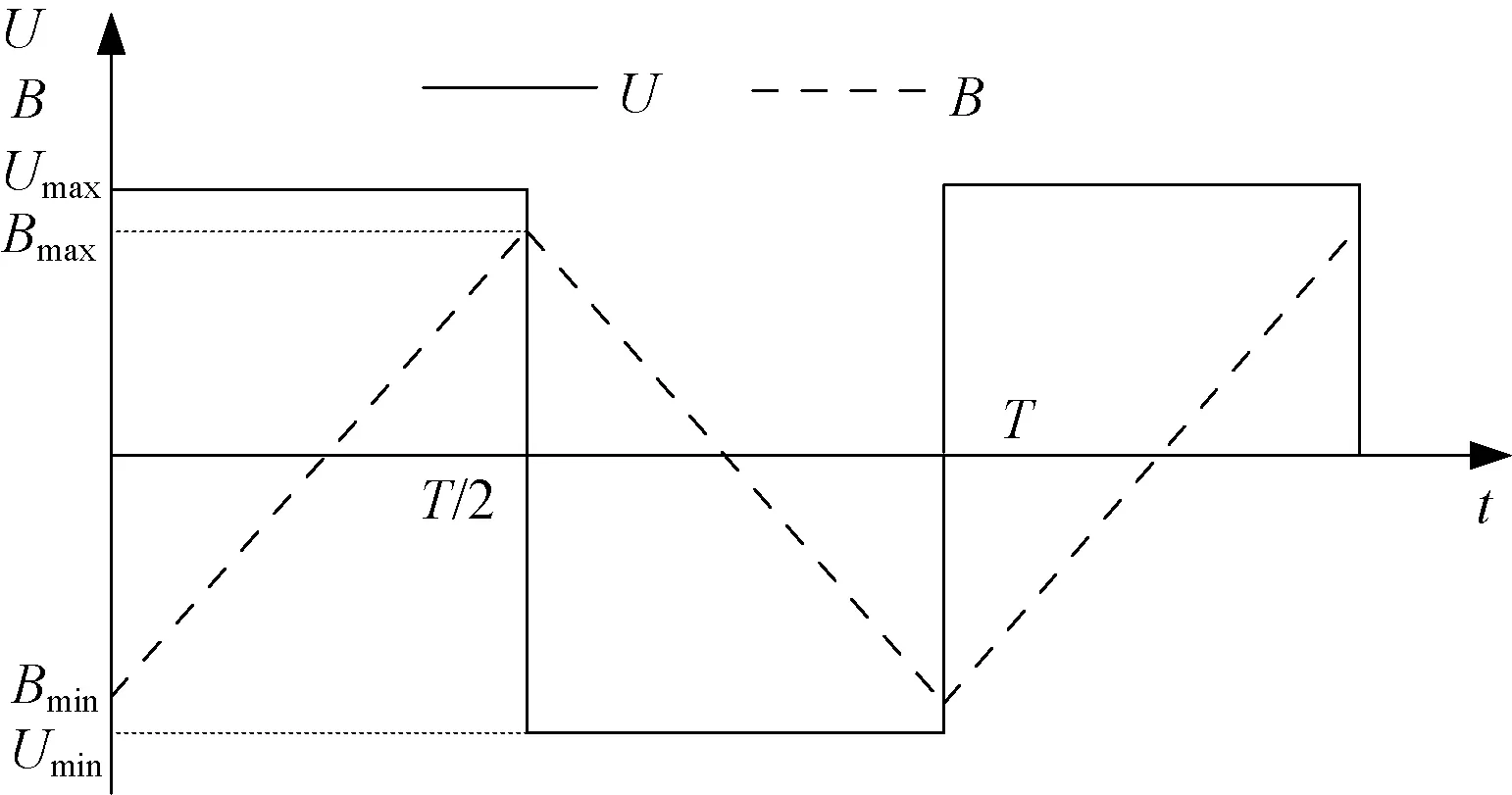
图2 方波激励及磁通波形Fig.2 Square wave and corresponding flux curve

对于方波电压有：

(29)

(30)

Um=4fNSBm

(31)

因此，方波电压激励下的磁心损耗计算式为：

(32)

3.3 Barbiso算法

在三角波电压激励下，由法拉第电磁感应定律可得：

(33)

因此，利用式(17)可得三角波激励下的磁心损耗表达式为：

(34)

同理，在方波电压激励下有：

(35)

因此，利用式(17)可得方波电压激励下的磁心损耗表达式为：

(36)

4 实验验证与结果分析

基于CSW可编程电源的磁心损耗测量系统如图3所示，对硅钢、非晶及纳米晶磁环模型进行高压侧空载实验。其中，可编程电源可以输出三角波、方波等各种非正弦波形，输出频率范围为0.04～5kHz，输出电压峰值为312V。

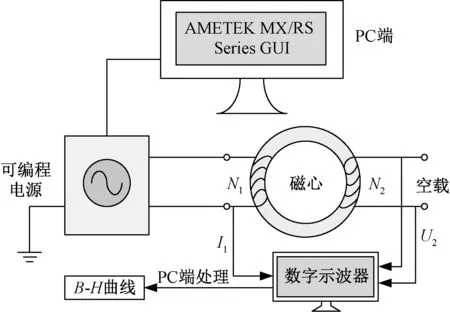
图3 磁心损耗测试系统Fig.3 Test system of core losses

根据数字示波器采集的原边电流I1和副边空载电压U2，基于安培定律与法拉第电磁感应定律可分别得到磁心的磁场强度H与磁感应强度B：

(37)

(38)

式中，N1、N2分别为原边和副边线圈匝数；l为磁心等效磁路长度；Se为铁心等效截面积。

在得到一个磁化周期的磁场强度H与磁感应强度B后，即可获取磁心的磁滞回线，而该磁滞回线面积等于磁心的损耗值大小，如式(39)所示：

(39)

硅钢、非晶及纳米晶3种磁环的参数见表2。在试验过程中，采用调节激励电压幅值的方法来控制磁心工作于采样磁感应强度。

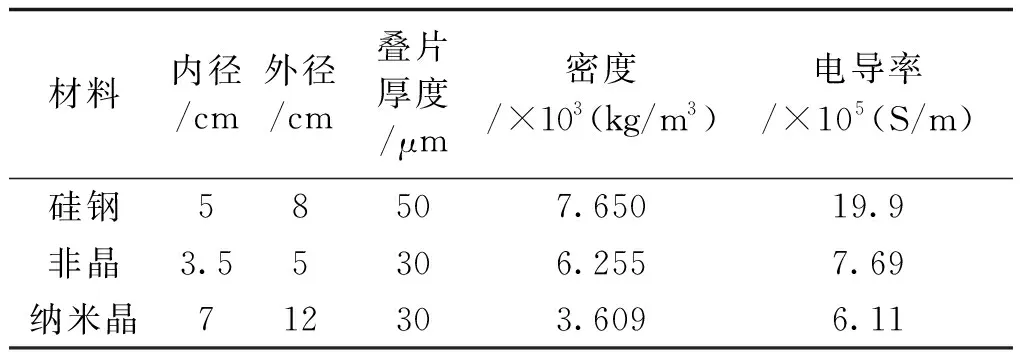
表2 硅钢、非晶及纳米晶磁环参数Tab.2 Parameters of silicon steel, amorphous and nanocrystalline magnetic core

在三角波与方波激励下，3种磁环选择的磁感应强度峰值Bm测试点分别为0.13T、0.24T、0.33T、0.40T、0.46T、0.53T和0.66T，频率测试点f为2000Hz。

4.1 参数提取

利用实验室的软磁交流测试系统，分别测量正弦波激励下，硅钢、非晶及纳米晶3种磁环在0.1～0.8T(步长0.1T)磁感应强度峰值点，以及100Hz、200Hz、400Hz、600Hz、800Hz、1000Hz、1200Hz、1500Hz、2000Hz、2500Hz频率点处的损耗值。

基于以上不同磁感应强度峰值及频率点的损耗值，提取出的Boglietti算法的损耗系数见表3。

表3 三种材料的损耗系数Tab.3 Loss coefficients of three magnetic cores

根据Barbiso算法参数的提取特点，其应选择的正弦激励磁感应强度峰值Bm测试点应与非正弦激励对应，即Bm分别为0.13T、0.24T、0.33T、0.40T、0.46T、0.53T和0.66T。

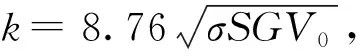
(40)

当Bm=0.66T时，(W-Wcl)与f1/2的线性回归方程如图4所示。易得，此时硅钢磁环对应的磁滞损耗Wh和系数k分别为：

Wh=5.519 mJ/kg，k=0.10534 mJ/(kgT1.5Hz0.5)

图4 Bm=0.66T时，硅钢磁环总损耗与涡流损耗的差值与频率1/2次幂的线性回归方程Fig.4 Linear regression equation of total loss and eddy current loss difference versus f1/2 with Bm=0.66T in silicon steel ring

由于利用k已可方便求解任意激励下的磁心损耗，因此不需要再将其转化为V0。在Barbiso算法中，硅钢磁环的损耗相关系数见表4。

在Amar算法中，硅钢磁环在给定参考频率f0=1000Hz下的损耗相关系数见表5。

4.2 实验与计算结果

为了对3种损耗算法的误差进行分析，本文引入全局平均相对误差的概念。全局平均相对误差计算式为：

(41)

式中，Pi,cal、Pi,mea分别为第i个计算值和测量值。

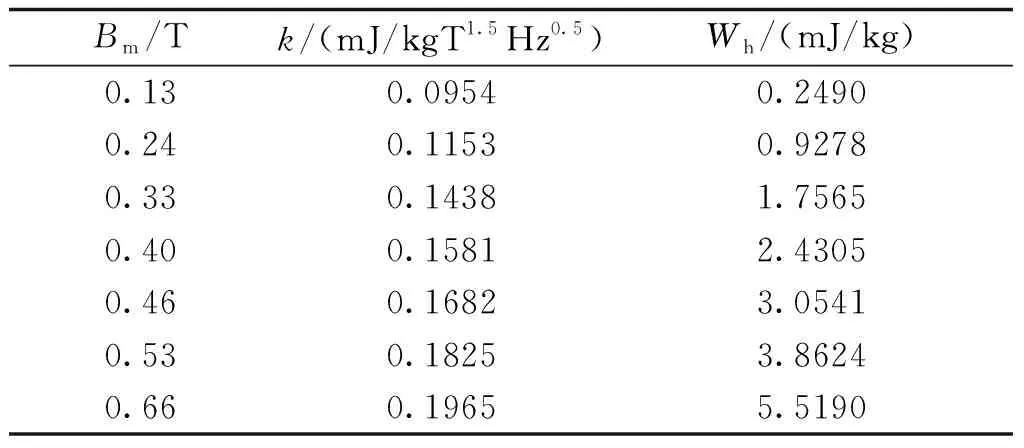
表4 硅钢磁环的损耗相关系数Tab.4 Loss coefficients of silicon steel ring

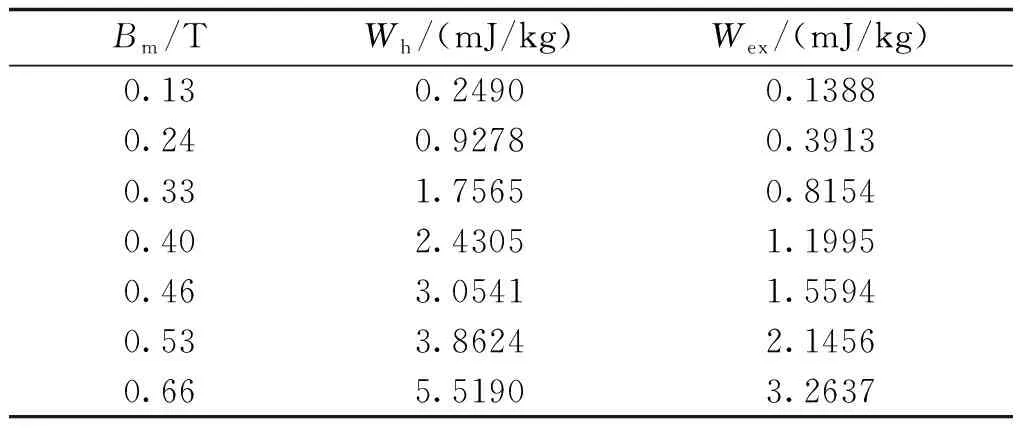
表5 1000Hz频率下硅钢的损耗系数Tab.5 Loss coefficients of silicon steel ring at 1000Hz

在三角波及方波激励下，硅钢、非晶及纳米晶磁心的测量值与基于三种损耗算法的计算值之间的对比结果如图5～图10所示，全局相对误差见表6。

图5 2000Hz三角波激励下硅钢磁环损耗结果对比Fig.5 Comparison results of triangle wave excitation at 2000Hz in silicon steel ring

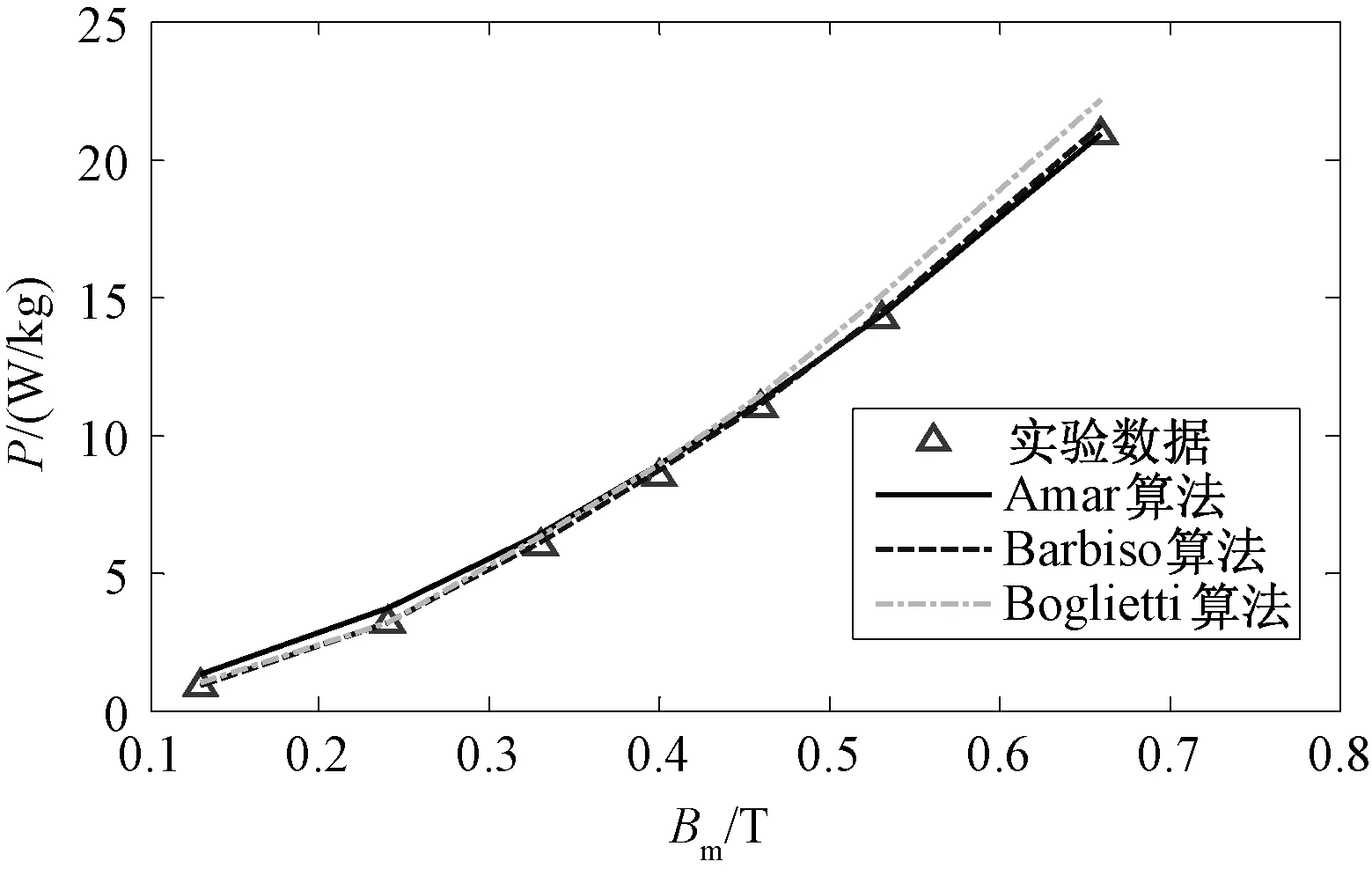
图6 2000Hz方波激励下硅钢磁环损耗结果对比Fig.6 Comparison results of square wave excitation at 2000Hz in silicon steel ring

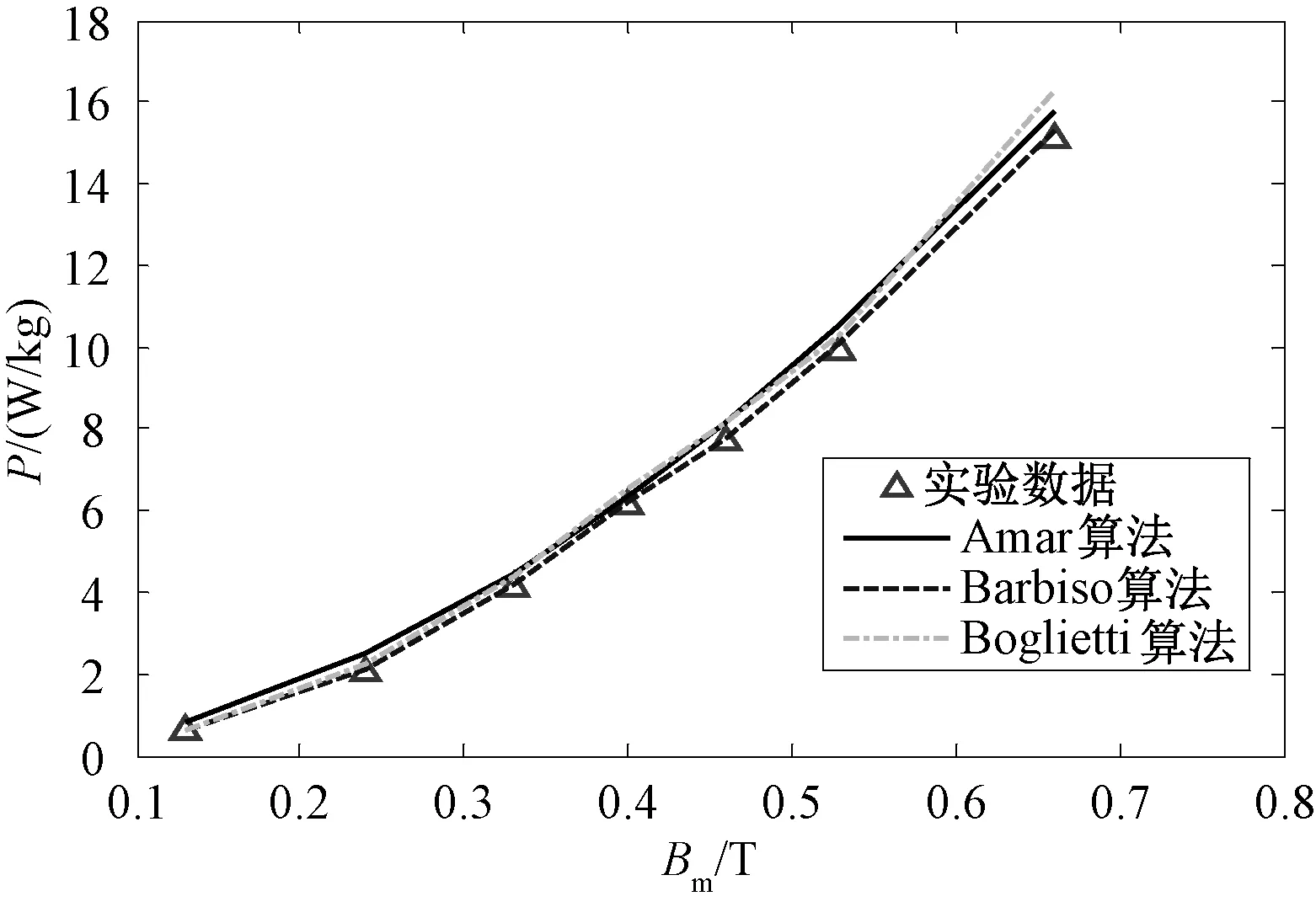
图7 2000Hz三角波激励下非晶磁环损耗结果对比Fig.7 Comparison results of triangle wave excitation at 2000Hz in armorphous ring

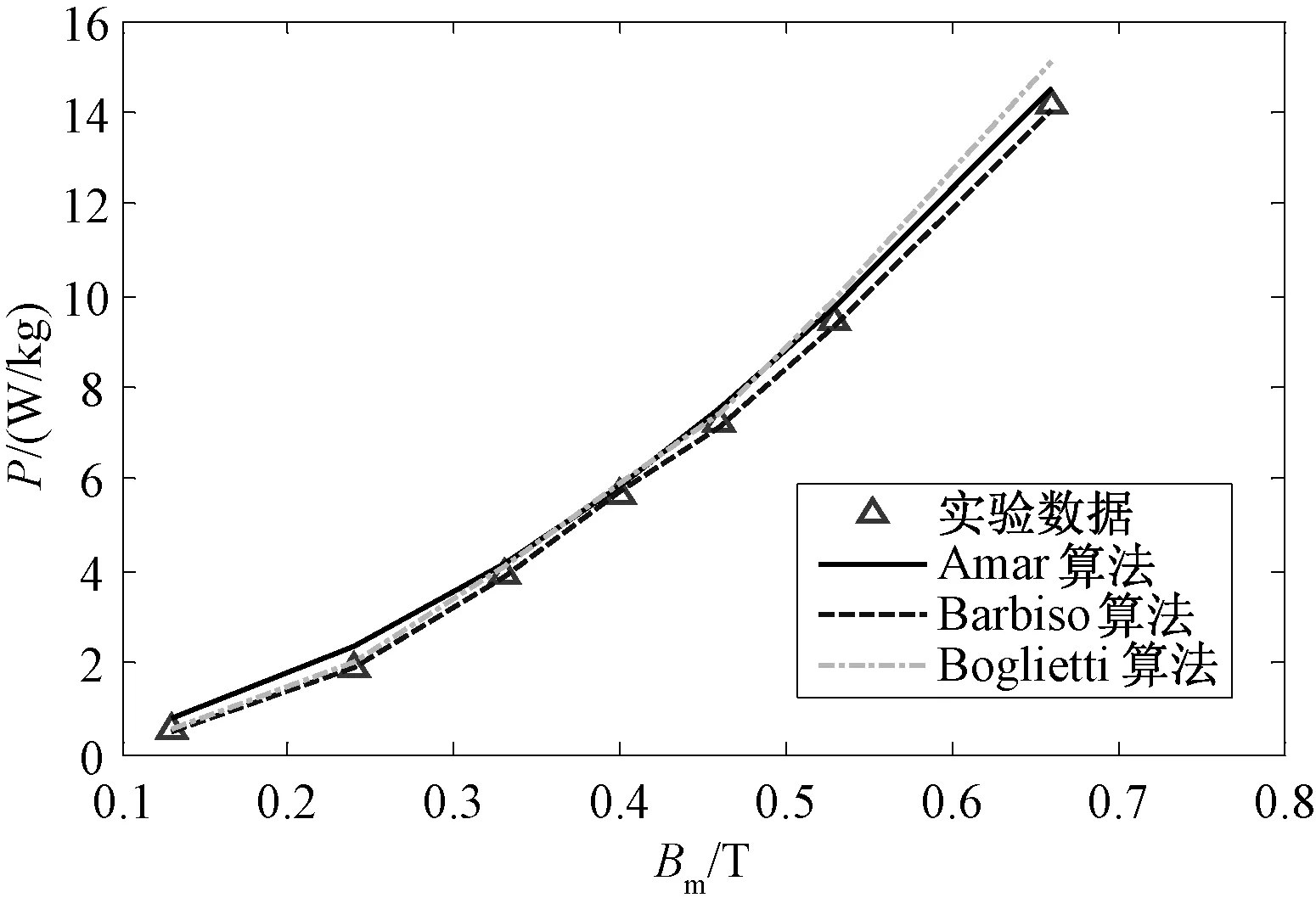
图8 2000Hz方波激励下非晶磁环损耗结果对比Fig.8 Comparison results of square wave excitation at 2000Hz in armorphous ring

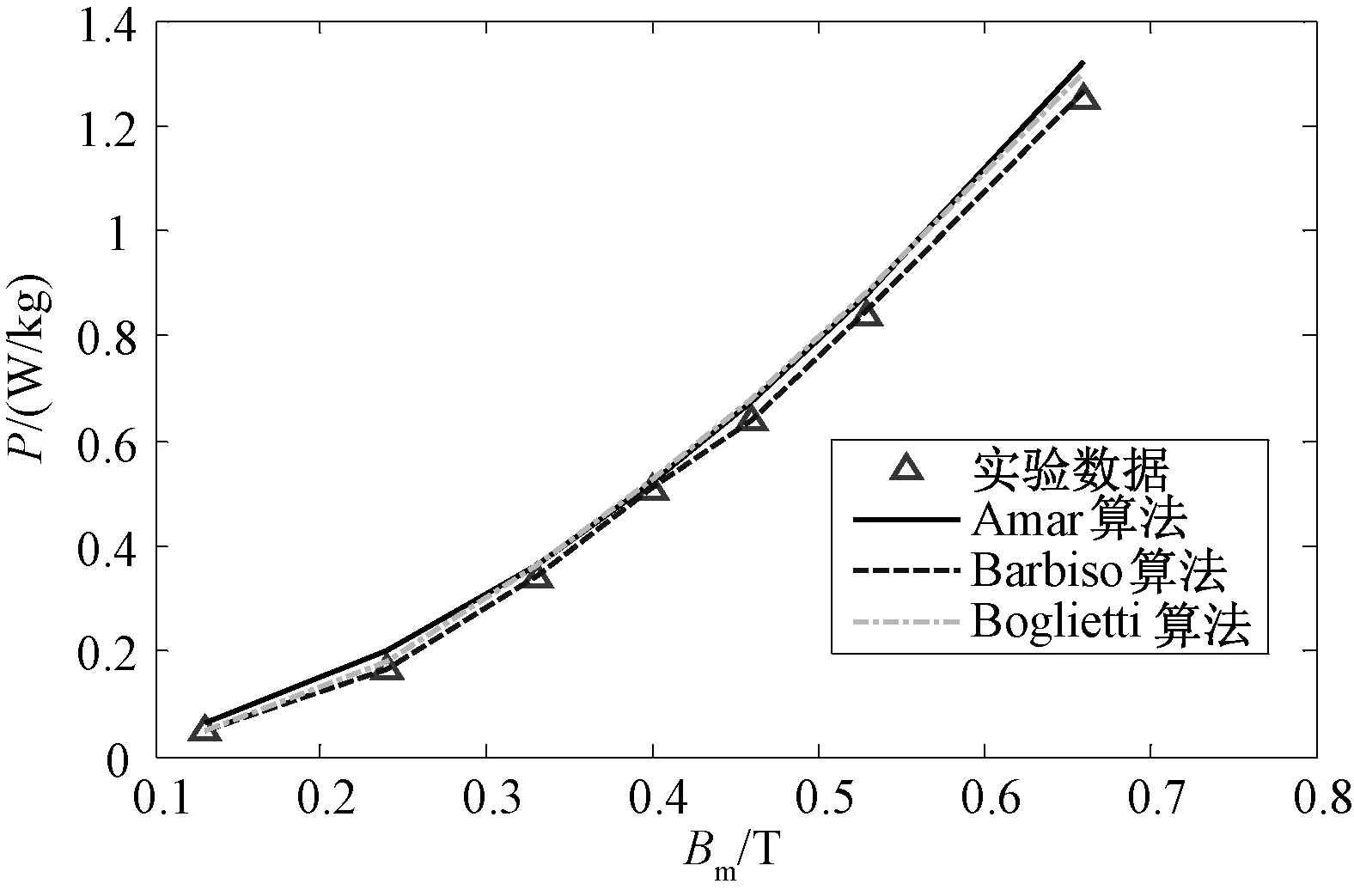
图9 2000Hz三角波激励下纳米晶磁环损耗结果对比Fig.9 Comparison results of triangle wave excitation at 2000Hz in nanocrystalline ring

从表6中可以看出：

(1)硅钢、非晶及纳米晶3种磁心在三角波、方波非正弦激励下，采用Barbiso算法求解损耗的精度均最高，最大误差仅为2.42%；其次是Amar算法，最大误差为6.16%；最后是Boglietti算法，最大误差高达13.37%。

(2)3种损耗算法在非晶及纳米晶两种新型磁性材料的计算误差与硅钢类似；同时，在相同磁感应强度及频率的工况下，非晶的损耗小于硅钢，而纳米晶的损耗却远小于其他两种材料。

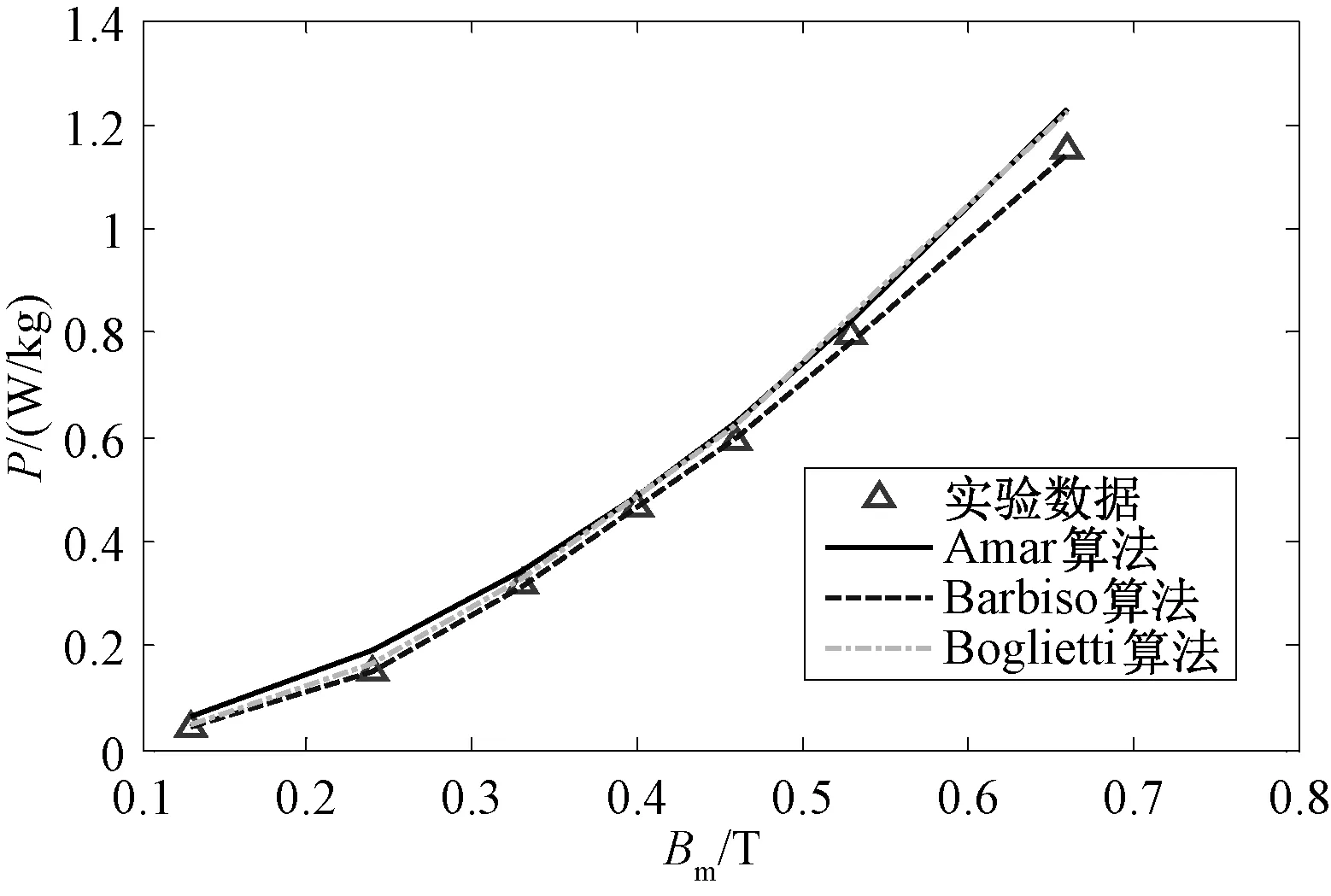
图10 2000Hz方波激励下纳米晶磁环损耗结果对比Fig.10 Comparison results of square wave excitation at 2000Hz in nanocrystalline ring

材料Amar算法Barbiso算法Boglietti算法三角波方波三角波方波三角波方波硅钢5.855.362.102.4211.5711.20非晶6.164.982.272.1611.7912.98纳米晶5.785.272.132.0512.013.37

4.3 误差分析

4.3.1 实验误差

首先，磁心损耗测试实验不可避免地会存在误差。例如，可编程电源无法产生完全理想的三角波与方波激励电压；同时，数字示波器本身存在测量误差，从而使输出的电压、电流波形产生误差，进而导致最终通过实验测量得到的磁心损耗出现一定的误差。

4.3.2 理论误差

Amar算法与Boglietti算法均是从频域的角度求解非正弦激励下的磁心损耗，运用傅里叶变换将非正弦激励转化为各阶次正弦谐波，再运用线性叠加的方式得到非正弦激励下的磁心损耗。然而，硅钢、非晶及纳米晶等磁性材料均具有复杂的非线性，通过简单线性叠加的方法必然会导致其与实际测量结果不符，从而使损耗计算产生较大的误差。

运用频域的方法求解磁性材料损耗，其损耗系数应为频率与磁感应强度的函数，不然则求解精度较低[17-19]。但是，要获取这种函数必须进行大量的实验，以此得到较大频率及磁感应强度范围内的损耗数据，继而基于多项式拟合的方法得到该函数。显然，这种做法并不能从磁心损耗产生的物理意义出发，仅通过大量实验数据拟合损耗系数的方式提高频域损耗算法的求解进度，因此并不实用，使用者较少，无法满足磁心优化设计等领域损耗“快速”求解的需求。

与此同时，Amar算法与Boglietti算法在推导过程中，为将复杂的损耗计算公式进行简化，均进行了近似处理。其中，Boglietti算法忽略剩余损耗分量[14]，而Amar算法将非线性相关项用波形系数进行了近似替代[13]。这些处理方式同样会降低损耗算法的求解精度。

与Amar算法及Boglietti算法不同，Barbisio算法从时域的角度求解磁心损耗，保留了非正弦电压激励波形的原始时域变化特征，同时考虑了磁性材料的非线性特性，并且该算法考虑了Bertotti损耗统计理论中的剩余损耗，同时也未进行近似处理。因此，从表6中可以看出，Barbisio算法的求解精度明显高于其他两种算法。

通过上述分析可知，在计算精度方面，Barbisio算法明显高于Amar算法和Boglietti算法；而在模型参数提取复杂程度上，Amar算法最高，而Barbisio算法与Boglietti算法则相对较低，复杂程度相当。因此综上所述，可得如下结论：Barbisio时域损耗算法在准确性与实用性两方面具有最优的综合性能，建议在磁心优化设计等领域采用该算法求解磁性材料在非正弦激励下的损耗。

5 结论

(1)硅钢、非晶及纳米晶3种材料在三角波及方波激励下，基于Barbiso算法求解损耗的精度均最高，其次是Amar算法与Boglietti算法；而在模型参数提取复杂程度上，Amar算法最高，其他两种算法较低，复杂程度类似。因此，在非正弦激励下，Barbiso算法是综合性能最优的非正弦激励磁心损耗计算方法，建议在电力电子装置内部磁心元件的优化设计等工程应用领域，优先选择Barbiso算法求解非正弦激励下的磁心损耗。

(2)首次将上述3种算法运用于非晶及纳米晶中，并进行了实验验证，发现其在非晶及纳米晶的求解精度类似硅钢。因此，3种算法在不同程度上同样适用于非晶及纳米晶的损耗求解，但Barbiso算法求解精度最高，综合性能最好。