计及储能和用户需求响应的并网型微网优化调度模型

李盛伟， 李鹏飞， 白星振， 葛磊蛟

(1. 国网天津市电力公司经济技术研究院， 天津 300171；2. 山东科技大学电气与自动化工程学院， 山东 青岛 266590；3. 天津大学电气自动化与信息工程学院， 天津 300172)

1 引言

目前，由于光伏发电具有间歇性和波动性等特点，大规模的光伏并网和消纳比较困难。所以在含光伏的微网中配置合理容量的储能，是促进分布式光伏就地消纳、提高光伏系统效能、降低经济成本的有力方式[1-3]。随着智能电网的发展与完善，相较于传统电网而言，电能需求的增长逐渐拉大了区域的负荷峰谷差，使得需求响应(Demand Response，DR)得到更广泛的关注，需求侧资源的参与成为微网优化运行中不可忽视的因素。因此，研究储能系统(Energy Storage System，ESS)和需求响应对微网成本优化的影响，对并网型光伏微网的日前经济运营优化有着重要意义。

本文将储能系统和需求响应引入并网型光伏微网，在日前优化调度下，达成需求侧资源参与协调优化的目的。目前，国内外学者就需求侧资源参与微网运行的问题进行了大量研究。其中，针对储能系统，文献[4-6]对不同策略下含储能系统的微网优化配置展开了研究，并给出了各策略的微网优化方案。文献[7]基于不同的运行模式，分析了分布式发电系统(Distributed Generation，DG)和储能装置的基本出力特性，按经济最优原则制定了运行方案，但对并网安全方面考虑稍有不足。针对需求侧响应，文献[8,9]综合考虑需求响应对光伏微网经济性的影响，并分析了储能系统以及需求响应对光伏微网投资决策的重要意义。文献[10]基于需求侧的不确定性，搭建了需求响应和储能系统的模型，并对微网的随机出力优化调度进行了仿真研究，但在需求侧响应的过程中未考虑负荷的用电满意度问题。

本文基于上述问题提出一个综合考虑储能、需求响应和用户满意度的并网型微网日前优化调度模型，通过改进遗传粒子群算法进行分析计算，兼顾用户满意度和微网经济性。文中最后通过四个方案分析比较，并利用仿真，验证所提模型的有效性。

2 微网系统组件模型

2.1 光伏发电系统模型

光伏发电利用半导体界面的光生伏特效应将太阳能直接转换成电能。而光伏发电的输出功率会随着光照强度和环境温度等因素的变化而变化，具有一定的随机性和波动性。

光伏发电系统在标准太阳辐射强度GSC(一般为1000W/m2)、相对大气光学质量为AM1.5、电池温度TSC为25℃的情况下，输出功率为：

(1)

2.2 蓄电池储能系统模型

储能系统具有负荷和电源的双重特性，在低负荷时段，储能系统能够作为负荷将电能特别是多余的新能源发电量储存起来；而在高负荷时段，储能系统又可以将之前储存的电能释放出来，为电力系统供电，减少电力系统的供电压力。在微网运行的过程中，储能系统储电量与荷电状态 (State Of Charge，SOC) 有关，t+1时刻与t时刻的储能蓄电池系统功率关系可表示为：

(2)

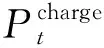
2.3 需求响应模型

文献[12]提供的DR分时电价(Time-Of-Use，TOU)模型如图1所示。通过TOU方法，将负荷百分比从峰值时间段转移到非高峰时段，由微网操作者降低负荷，从而降低预期运行成本。

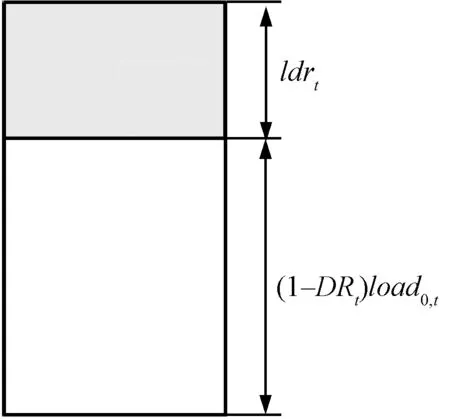
图1 考虑分时电价的DR负荷模型Fig.1 Load modeling considering TOU rate of DR

根据TOU方法的定义，本部分模型目的是将负荷曲线的部分负荷从高峰时段转移到非高峰时段，从而降低微网的预期运行成本。根据式(3)定义TOU方式的数学模型：

loadt=(1-DRt)load0,t+ldrt

(3)

式中，loadt表示考虑DR后t时刻的实际负荷；DRt表示t时刻参与DR负荷占基础负荷的比例；ldrt表示t时刻通过DR的转移负荷；load0,t表示不考虑DR时t时刻的基础负荷。

2.4 分布式发电机组模型

在微网中，除了光伏发电机组还有另外一些能源机组，例如微型燃气轮机和小型发电机组等。为了计算方便，根据文献[13]将这些机组统一看做为一个拥有独立成本系数的特殊机组，其成本可表示为：

(4)

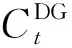
2.5 与大电网功率交互模型

微网中自身发电出力不足以满足当地负荷需求时，需从大电网购电以满足本地用电需求及旋转备用，本着“自给自足，余电上网”的原则，当微网的发电出力富足时，可以将多余的电兜售给电网，功率交互成本模型为：

(5)

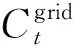
3 并网型微网优化调度模型

3.1 目标函数

在含多种需求侧资源参与的并网型微网的综合经济调度中，光伏发电消纳量最大、系统运行成本最低和系统煤耗最小是几种常见的优化模型。本文以系统运行成本最低为优化目标，建立一个包含光伏系统、储能系统、分布式发电机组和需求响应的微网综合优化调度模型，该模型为单目标非线性规划模型，目标函数为：

(6)

3.2 约束条件

3.2.1 功率平衡约束

系统运行功率平衡如式(7)所示：

(7)

根据式(7)可知，微网从电网购电量、分布式发电系统和储能系统的出力由DR决定，储能系统的放电模式可以看做是特殊的发电机，充电模式可以看做是特殊的负载。

3.2.2 微网稳定性约束

在微网运行的过程中，为了保证系统运行的稳定性还有留有一定的旋转备用，作为对突发供电需求的应对，其对应关系为：

(8)

另外，微网与大电网功率交互过大时，容易对电网运行的稳定性造成一定的影响，为了最大限度地避免这种影响，对两者的功率交互做了约束，如式(9)所示：

(9)

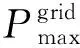
3.2.3 储能系统功率约束

根据文献[14]，与储能系统相关的限制约束如下所示。

储能系统的初始能量极限方程为：

(10)

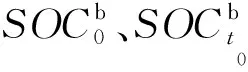
储能系统的充放电功率限制约束为：

(11)

(12)

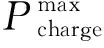
蓄电池的寿命与充放电深度相关，过冲和过放都会增加蓄电池寿命损耗，所以需对蓄电池荷电状态SOCt进行约束，储能系统的存储限制约束为：

(13)

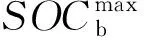
储能系统充电和放电的二元模型为：

(14)

3.2.4 需求响应约束

负荷转移不影响总负荷的大小，其约束为：

(15)

任意时段负荷转移存在上限，以免造成不必要的经济损失，对此用式(16)进行约束：

(16)

为了保证用户用电质量，最大负荷转移限制如式(17)所示：

(17)

3.2.5 分布式发电约束

分布式发电包括光伏发电和分布式机组发电两部分，式(18)给出了光伏发电约束，式(19)、式(20)分别对分布式机组发电的每小时输出功率和每日的输出功率进行约束：

(18)

(19)

(20)

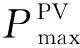
3.2.6 用户满意度约束

用户满意度分别由需求响应满意度和供电满意度构成[15]。需求响应满意度要求负荷需求被及时满足时，需求响应转移的负荷量越少满意度越高；供电满意度基于“自发作用，余量上网”的光伏政策，光伏发电就地使用，减少外送。如果本地用户的负荷都是由光伏系统与储能系统提供，则供电满意度最高。由此可知，用户满意度Se可用式(21)～式(23)表示。

(21)

(22)

(23)

式中，Ssup表示供电满意度；PDG,all表示分布式电源供电总量；PPV,all表示日光伏发电的总量；PESS,all表示储能供电总量；Sdr表示需求响应满意度。

在本文中，满意度虽然不作为最终的优化目标，但是会对优化过程起到一定的约束。并且在最终的结果分析过程中，满意度也会作为一个重要的参考因素。满意度约束为：

Se≥Smin

(24)

式中，Smin表示微网允许的最低满意度。

4 改进遗传粒子群算法求解优化调度模型

微网日运行优化过程中约束较多，传统粒子群算法在处理此类非线性优化问题时往往存在收敛速度慢、易陷入局部最优等缺点，为此本文将种群亲和度[16]的概念引入到粒子群算法中，并选用自适应的交叉、变异算子，提高目标求解效率，增强种群多样性，防止早熟现象的发生。同时利用亲和度的概念增强群体的优越性，避免局部收敛，最终完成对微网操作成本的优化。

在生成初始种群{X1,X2,…,Xn}的过程中，利用欧几里得距离求取计算种群个体相似性，如式(25)所示：

(25)

式中，1≤i,j≤n。

若d越小，表明粒子间的相似性越大，如果d等于0，说明两个粒子完全相同。本文引入一个近似系数τ，于是粒子亲和度的定义为：

(26)

计算粒子亲和度后将初始种群存入最优种群H中。在每次迭代后，对粒子进行交叉、变异获得新的种群。算法中采用自适应算子，粒子i的交叉、变异概率计算如下：

(27)

(28)

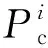
将新获得的种群存入H中，并进行亲和度计算，若种群个体超过H所容纳的数量，则淘汰掉亲和度低的个体。

本文提出的并网型微网日前随机优化调度模型求解的具体步骤如下：

(1)生成初始种群P0以及初始速度V0，并计算出个体最优值Pbest和全局最优值Gbest。

(2)将初始的个体值存入最优种群H中。

(3)完成种群更新和速度更新。

(4)对于更新完成之后的种群进行选择、交叉和变异，如果交叉变异后的目标值优于原先值，存入最优种群H中；否则舍弃本次交叉、变异，进入步骤(5)。

(5)利用亲和度机制式(25)、式(26)对H中个体的亲和度进行计算，如果超出H的最大容量，则根据亲和度大小，删除亲和度小的个体。

(6)更新个体最优值Pbest和全局最优值Gbest，若满足结束条件，进入步骤(7)；否则返回步骤(3)。

(7)输出最优种群和全局最优值Gbest。

5 算例

本文所研究的微网系统由分布式光伏、分布式发电机组、储能系统以及负荷构成，负荷包括主要可转移负荷和其他负荷，微网系统的结构如图2所示。

图2 微网结构图Fig.2 Structure of microgrid

5.1 基础数据

分布式发电机组、光伏发电系统、储能蓄电池的运行参数分别如表1～表3所示。某地的日预测温度和辐射强度数据如表4所示[17]。

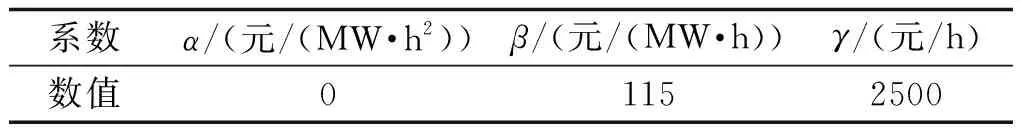
表1 DG机组的成本系数Tab.1 Cost coefficient of DG

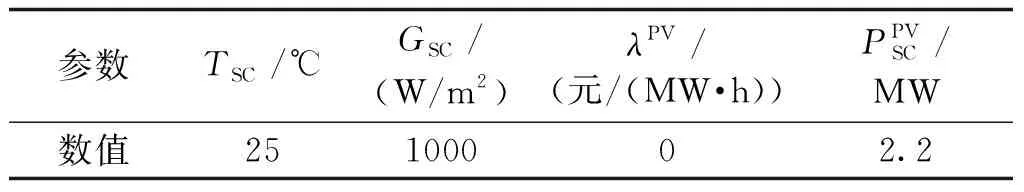
表2 光伏发电系统参数 Tab.2 PV system parameters

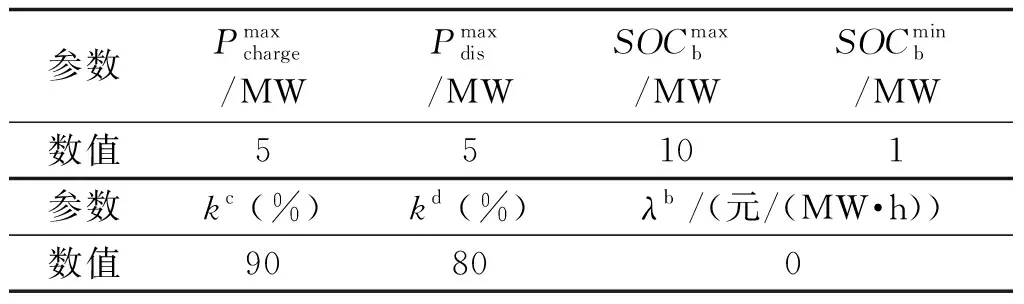
表3 储能系统参数Tab.3 Energy storage system parameters

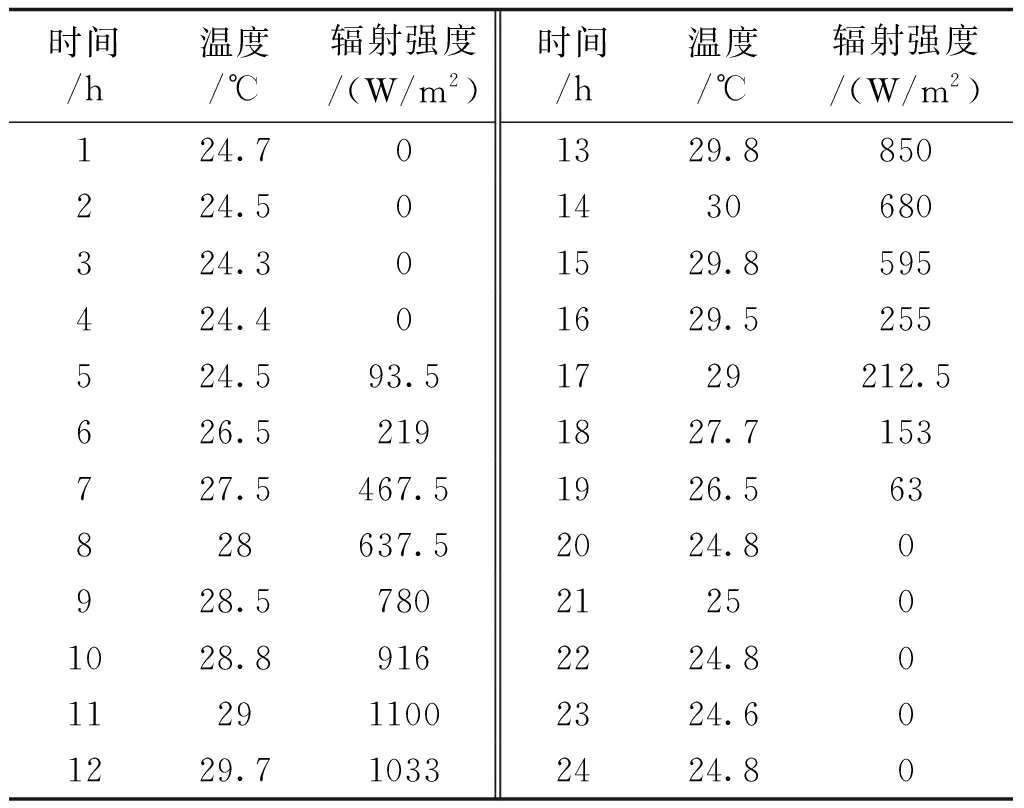
表4 预测的日温度和辐射强度数据Tab.4 Forecasted daily temperature and insulation for sample day

本文设定DG机组每小时最大出力为30MW；考虑微网与大电网功率交互限制为40MW；针对满意度，分为四个阶段：0～0.5为不满意，0.5～0.7为一般满意，0.7～0.8为很满意，0.8～1.0为非常满意。本文要求用户的用电满意度不得低于0.7；假设微网向大电网购电价格与售电价格相同，本文设定可转移负荷的固定补偿电价为0.7元/(kW·h)；另外，旋转备用价格假设为大电网购电价格的10%[18]。

5.2 算例分析

本文调度周期为1天，某地日预测负荷需求和微网向大电网的购电价格分别如图3、图4所示。

图3 微网的日预测负荷曲线Fig.3 Forecasted demand profile of microgrid

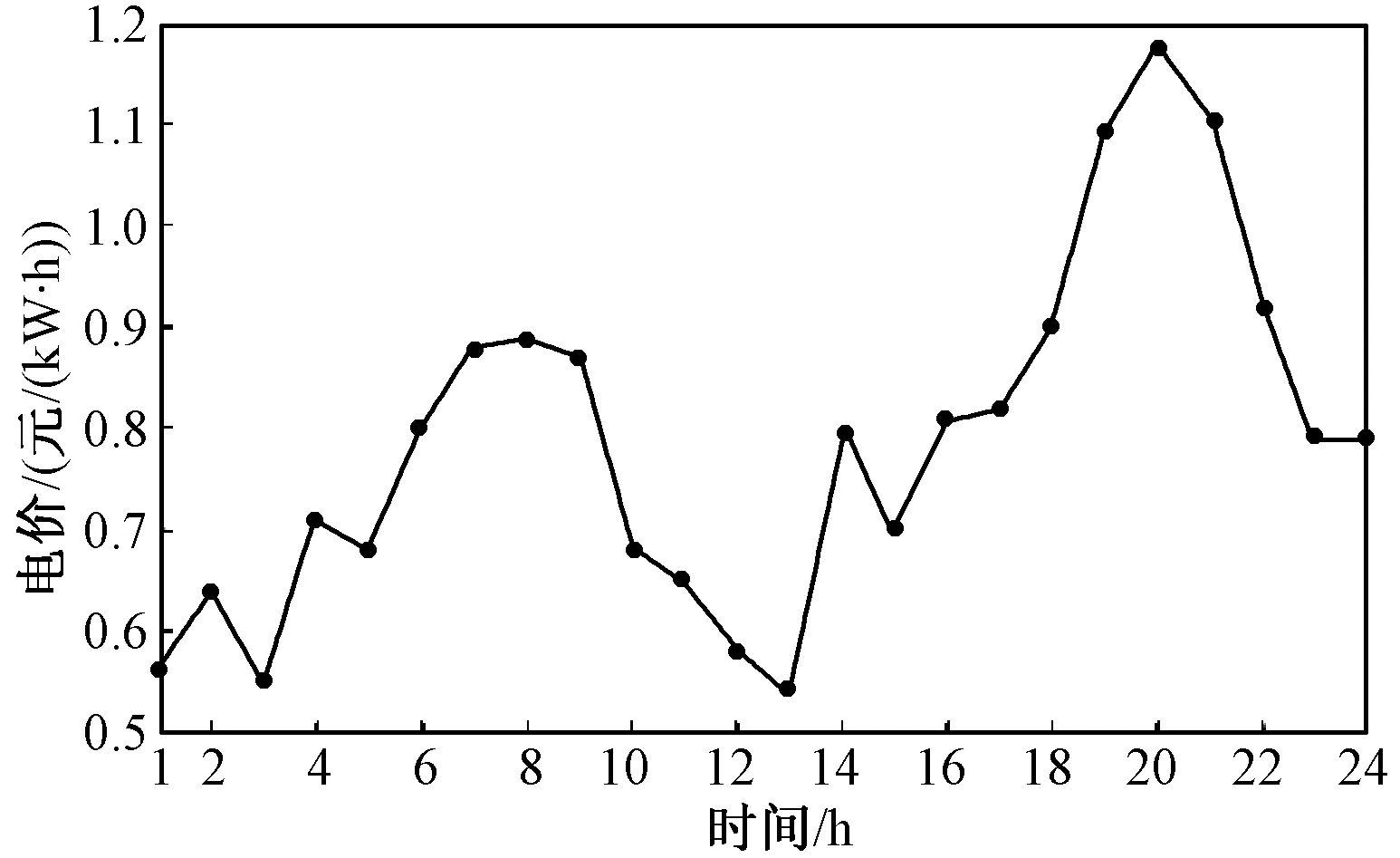
图4 购电价格曲线Fig.4 Forecasted upstream grid price

为了表现出ESS和DR对该优化模型的影响以及优化模型的有效性，设置四个方案进行分析比较。

(1)方案1。基础方案，不依赖ESS和DR，只通过光伏系统、分布式机组和购电来满足日预测负荷需求。

(2)方案2。ESS方案，不依赖DR，通过光伏系统、分布式机组、购电和储能系统来满足日预测负荷需求。

(3)方案3。DR方案，不依赖ESS，通过光伏系统、分布式机组、购电和需求响应来满足日预测负荷需求。

(4)方案4。综合方案，通过光伏系统、分布式机组、购电以及综合考虑ESS和DR来满足日预测负荷需求。

四个方案优化对比结果如表5所示。可见，方案1的预期运行费用为326727元，引入ESS和DR后，微网的预期运行成本有了明显的减少。方案2～方案4相较于方案1，成本分别下降了2.41%、6.25%、7.91%，这说明通过引入ESS和DR能有效减少微网的供电压力，使负荷曲线更加平稳。分析方案2和方案3可知，不管是ESS还是DR两者都能降低经济成本，相比于前者DR的优化更为显著，但是用户满意度仅为0.72。而方案4的总成本最低，用户满意度也在一个较高的水准，说明ESS和DR的综合运用才是微网经济成本优化的最佳选择。

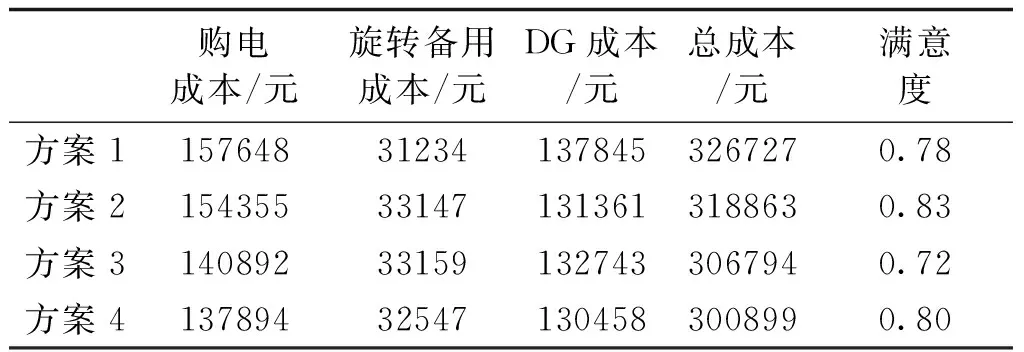
表5 四个方案的运营成本Tab.5 Operating costs of four schemes

图5为光伏发电的日出力曲线图。10∶00～16∶00时段为出力高峰，受外界因素影响较大。

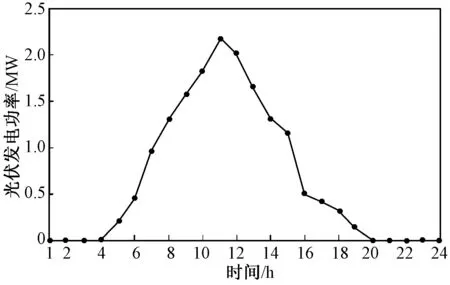
图5 光伏发电日出力Fig.5 Available power from PV system

图6为一天等效负荷的优化图。可以看出，相比于原始负荷而言，在综合考虑ESS和DR之后的负荷曲线，都体现了对负荷削峰填谷的效果。图7为方案2和方案4的储能系统的曲线图。可以看出，方案4在整体上更能调动资源的利用，ESS整体上保持一个较高的储能状态。

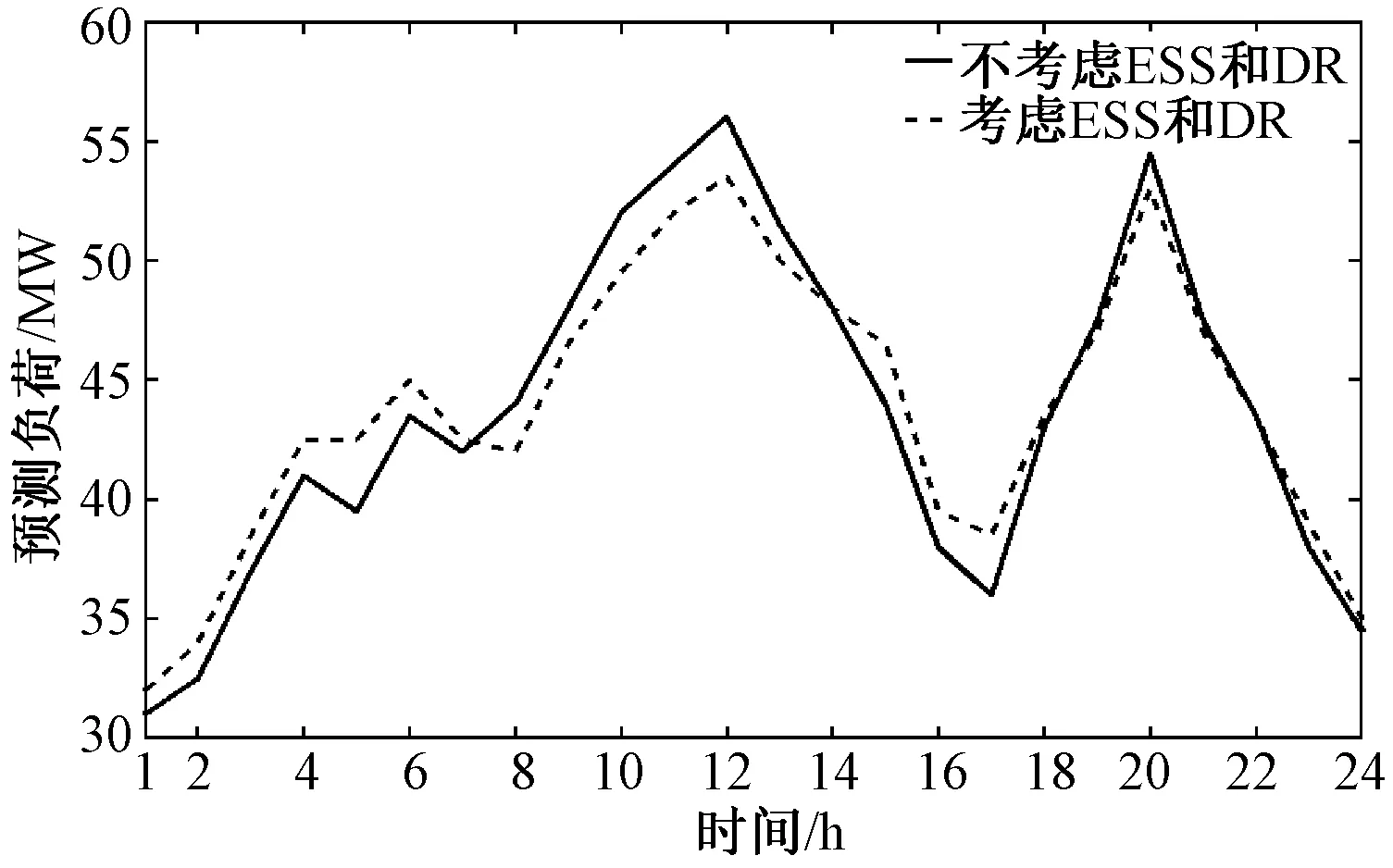
图6 负荷优化曲线Fig.6 Load optimization curve

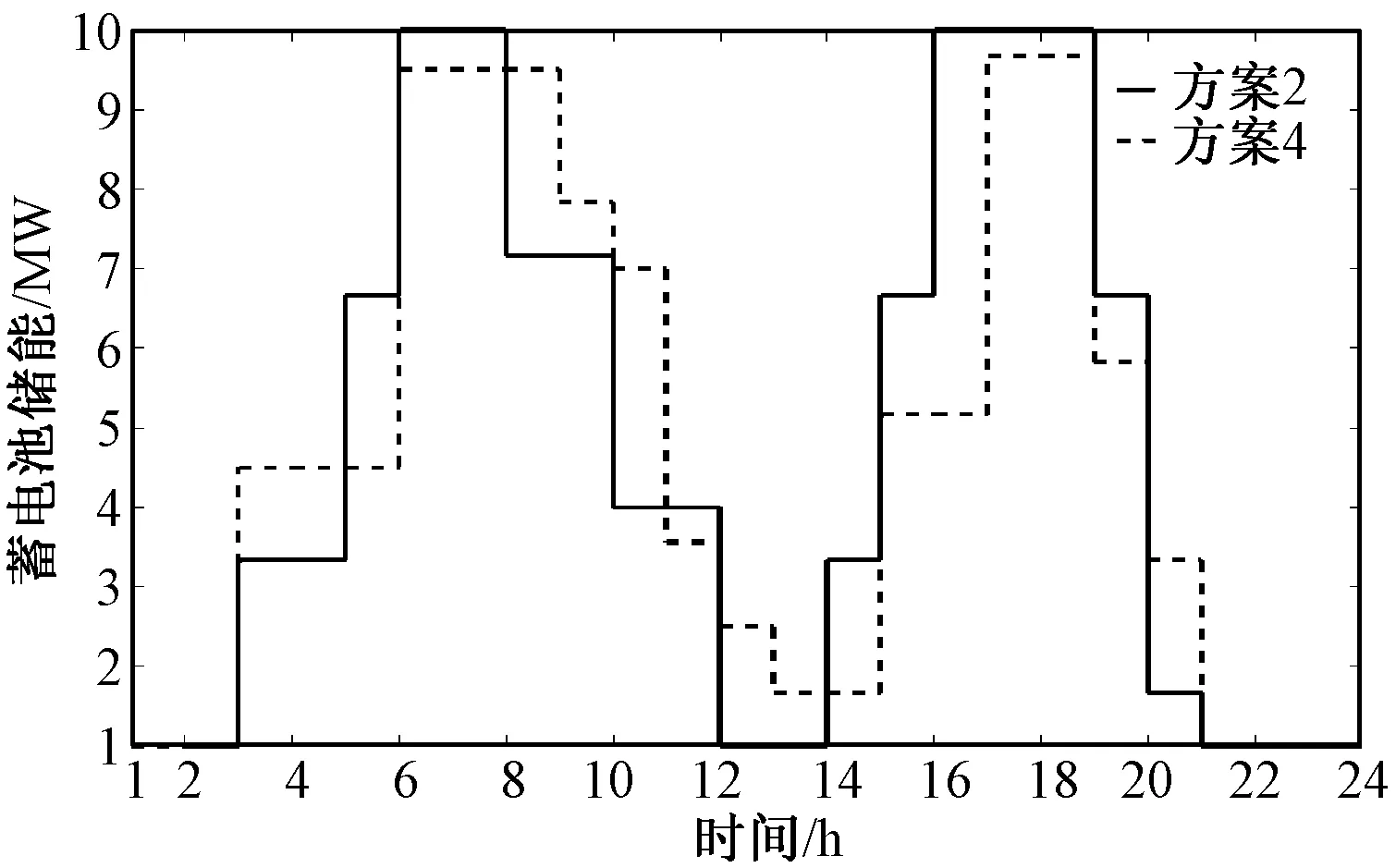
图7 ESS储能曲线Fig.7 Stored energy of ESS

分布式机组出力和购电功率曲线分别如图8、图9所示。方案4相较于其他方案，分布式机组出力曲线与购电功率曲线更加平稳，总量也要少于其他三个方案。这说明在加入ESS和DR后，微网日运行会降低对电网购电和成本较高机组的依赖，更多地通过负荷优化调度或者储能来调节满足日前用户的负荷需求，提高微网的经济效益。

图8 分布式机组出力曲线Fig.8 Purchased powers from DG

图9 购电功率曲线Fig.9 Purchased powers from upstream grid

6 结论

本文提出一种考虑需求侧资源参与优化的微网经济调度模型，该模型充分考虑了储能系统和需求响应在微网日前调度中的优化作用，降低了微网运行的成本并满足微网的“削峰填谷”需求，使得负荷曲线尽可能平缓，并最终维持一个较高的用户满意度水准。通过算例仿真分析，验证了模型的经济性和有效性，最后得出结论：在微网的日运行过程中，通过使需求侧资源积极参与优化调度能够有效降低微网成本，减少负荷的峰谷差，使系统更加经济、安全、稳定地运行。

需求侧资源积极参与电网优化控制，这是电力需求侧管理的重要内容之一。针对不同种类的负荷提供不同的赔偿机制以及优化策略，将是下一步的研究方向。