基于振动信号统计特性的变压器绕组状态监测

陈沛龙，刘 君，马晓红，王丰华，张 迅，胡兴海，许 逵, 黄军凯，曾 鹏，田承越

(1.贵州电网有限责任公司电力科学研究院，贵州，贵阳550002；2. 电力传输与功率变换控制教育部重点实验室，上海交通大学，上海 200240；3. 贵州电网有限责任公司兴义供电局，贵州 兴义 562400)

1 引言

变压器作为电力系统的重要连接环节，在电力系统中起着电压、电流变换以及电能分配和传输的重要作用。据统计，绕组变形是变压器的主要故障类型，且随着电网电压等级及变压器容量的增大，其故障率居高不下[1,2]。因此，积极开展变压器绕组状态监测，及时发现故障隐患，对确保电网的安全、优质、稳定及经济运行具有十分重要的意义。

近年来，振动分析法作为一种灵敏性较高的变压器绕组状态检测方法，引起了国内外研究人员的关注[3,4]。其原理是将变压器绕组视作一个机械结构体，当绕组出现松动或形变时，其机械性能会随之变化，故通过监测经由结构件或绝缘油传递至油箱壁的振动信号便可实现绕组状态的分析评估。其中，如何从监测到的振动信号中提取出合理有效的绕组状态监测指标一直是研究热点。文献[5,6]根据模型变压器空载试验和短路试验下的箱壁振动信号及其与变压器电压电流的关系，建立了基于振动信号100Hz分量的变压器振动模型，提出了根据振动信号100Hz分量的变化对绕组状态进行监测的方法。在此基础上，文献[7]考虑了变压器运行参数如电压电流等与振动信号的概率关系，基于自学习算法和贝叶斯网络提出了变压器概率振动模型来对绕组故障进行诊断。文献[8]以50Hz和100Hz及其倍频分量作为特征频率，建立了计及变压器运行参数的振动信号基频折算模型，根据不同频率分量的变化来诊断绕组状态。文献[9]给出了振动相关性、振动平稳性、能量相似度和频谱复杂度4种特征值来分析判断变压器的绕组变形。文献[10]根据变压器振动信号经验小波分解函数分量的Hilbert谱，构建了基于能量的特征矢量对变压器的典型工况进行识别。但上述研究大都在实验室条件下基于模型变压器或小变压器进行研究，考虑到变压器结构、运行条件及年限的分散性及与变电站现场运行环境的差异性，所提出的振动信号特征量的有效性仍有待进一步验证。文献[11]在考虑变压器运行参数的前提下，提出了基于广义回归神经网络的变压器振动基频幅值计算方法，应用某110kV在运变压器的表面振动信号验证了计算结果的有效性。人工智能时代对变压器振动在线监测获取的海量振动信号分析方法及其绕组状态识别方法提出了新的需求和挑战[12,13]，为提高在运变压器的运行可靠性，有必要进一步研究高效准确的变压器振动信号分析方法，实现变压器绕组状态的准确监测。

聚类分析作为数据挖掘的一种手段，能够快速、准确地从大规模的数据集合里发掘出其中有价值的数据分布、模式及规则。基于此，本文尝试利用系统聚类对变压器振动信号进行分析，依据从振动信号聚类结果中提取出的振动特征曲线并定义特征指标来判断绕组状态。最后以某500kV变压器振动在线监测系统的批量振动监测信号数据为对象，验证所提方法的有效性。

2 基于系统聚类的振动信号分析

根据变压器振动在线监测系统获取的振动信号特性，分别从振动信号标准化和信号截取两个部分进行振动信号预处理。

2.1 振动信号预处理

在对变压器海量振动监测信号进行处理时，为保持信号的形状并降低信号幅值对分析结果的影响，通常可对振动监测系统采集到的振动信号进行标准化处理。本文在此采用Z-score标准化法，计算公式为：

(1)

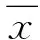
变压器振动在线监测系统持续对在运变压器的振动信号进行采集和存储时，以每相放置一路振动传感器、采样频率10kHz、存储间隔5min和每组信号大小10MB来计，一台变压器振动在线监测系统在1个月内存储的数据量可达约1GB左右。那么，经过较长一段时间的运行，在线监测系统获得的振动数据量将十分庞大，直接对其分析处理会存在计算量大、信号处理效率低等问题。因此，需要对待处理的振动信号进行截取处理，以简化计算量。本文对标准化后的振动信号进行了截取处理，具体方法如下：对监测系统经一定时间间隔存储的各组振动信号，从前两周期振动波形内的最低点起，截取长度为0.2s的振动信号。这样既缩小了待处理的振动信号数据规模，也不会影响变压器振动信号的原有波形结构。

2.2 系统聚类算法

系统聚类的基本思想如下：先将多个样本各自看成一类，然后规定样本之间的距离、类与类之间的距离，选择距离最小的一对并成一个新类，进而计算新类和其他类的距离，再将距离最小的两类合并，重复以上过程，直至各类的大小和形状趋于稳定[14]。与其他聚类方法相比，系统聚类算法具有距离定义简单、聚类质量不受初始聚类点影响等优势，尤其擅长处理连续性数据。此外，其分组过程的标准是基于对象特征的相异度，即同组中的对象相异度小，不同组中的对象相异度大，故可用来对运行中的变压器振动监测信号进行分析处理。具体步骤如下：

(1) 形成初始距离矩阵D0

(2) 距离矩阵的降维

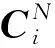
dtm=min(dti,dtj)

(2)

dtm=max(dti,dtj)

(3)

(4)

(5)

(6)

显然，选取不同的距离递推公式会对系统聚类结果产生不同的影响。因此，本文中引入聚类相关系数来检验不同距离递推公式产生的二叉聚类树和实际情况相符程度，在此基础上选择合适的距离矩阵降维方法，达到最优的聚类效果[16]。

聚类相关系数C的计算公式为：

(7)

一般来说，聚类相关系数值越接近于1，聚类效果越好。

(3)类簇合并

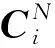
重复以上过程，直至最小元素dmin超过预先设定的聚类阈值或距离矩阵维数降至预设值，完成距离矩阵的降维。

因聚类个数的不同会对聚类结果中类簇的形状、所包含的数据量等造成一定影响，使得不同数据区间区分不够明显，最终有可能引起异常数据的误判，从而降低基于振动信号的变压器绕组状态诊断的准确性。因此，为较为准确地确定聚类的个数，使聚类后产生的各类簇之间相对稳定，本文根据类簇的总体距离来确定系统聚类数目，即将聚类结果中每一个类簇包含的所有样本数据对应的类簇中心距离进行累加，即可得到类簇总体距离J，其计算公式为：

(8)

(9)

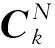
随着聚类个数N的增加，样本数据会被归入到距离最近的类簇中，从而导致总体距离J呈现不断减小的趋势，并逐渐稳定。总体距离J下降趋势减缓反映了聚类结果中的各类簇形状和大小相对趋于稳定。因此，本文选取总体距离下降减缓处的N值作为系统聚类个数。

2.3 振动特征曲线的提取

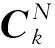
(10)

式中，K1,K2,…,KM分别为各个类簇中的振动信号数目；M为振动信号长度。

2.4 绕组状态监测方法

对变压器振动监测信号进行聚类分析的最终目的是使之服务于变压器绕组状态的准确监测。T2控制图是一种基于T2统计量的图形方法，它能够对生产过程的关键质量特性进行测量、记录、评估和监测，并判断过程是否处于控制状态[17]。因此，本文在此采用T2控制图来根据振动信号的聚类结果分析判断变压器绕组状态。所用的T2统计量由美国学者Hotelling提出，它从整体出发，能够检验多元变量的稳定性，因而适合于振动信号的异常判别。

对运行中的变压器来说，可将其振动信号的观测值视为服从正态总体N(μ,Σ)的独立同分布。此处，μ为总体均值；Σ为总体协方差矩阵。设特征参量X1,X2,…,Xp是从样本数量为l的振动信号中提取出的振动特征曲线，可构造待检测振动信号X的T2统计量为：

(11)

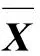
当样本数量足够大时，统计量T2表现为F分布，即

(12)

并且，其1-α的置信域为一个p维的椭球，由满足式(13)的全部X决定：

(13)

T2统计量通常描述的是样本到模型中心的距离，它反映了待检测的变压器振动信号偏离正常变压器振动信号特征曲线的程度，即偏离绕组正常工作状态的程度。因此，通过判断待检测振动信号的T2统计量是否在正常振动信号的置信区间内即可判断绕组状态是否正常。

具体应用时，即利用T2控制图对变压器绕组状态进行监测时，可根据求取出的置信区间设定控制上限UCL和控制下限LCL：

LCL=0

(14)

(15)

由根据统计学中置信区间的定义可知，置信区间1-α反映了待判断样本落入已知样本区间的概率，故本文在此取显著性水平α=0.05和α=0.01生成预警限和报警限。

对于每一个待检测振动信号，依次构造它的T2统计量。当变压器绕组状态异常时，其振动信号会明显偏离正常振动信号，相应地，该振动信号的T2统计量相对正常值会有所增加，依据T2控制图可以观测到这一变化。若振动信号的T2统计量超过控制上限，则该振动信号异常，表明此时变压器绕组可能存在故障，需要引起注意。此外，根据T2统计量的散点图的离散情况，也可以对振动信号异常的程度作出初步评估。

3 结果分析

以某500kV变电站变压器振动在线监测系统采集到的振动信号为聚类样本，该系统的采样频率为10kHz，主要对变压器的箱壁振动信号、工作电压和负载电流进行监测。其中，振动信号使用灵敏度为10mV/g的PCB加速度传感器进行采集，测点放置于变压器箱壁下方距离底座约1/4处较为平滑的位置，每相绕组放置一路振动传感器。图1为测点位置实物图。

图1 传感器位置实物图Fig.1 Real picture of vibration sensor placement

监测系统每5min存储一组数据，时间长度为10s。限于篇幅和显示方便，图2给出了变压器A相测点一段时间内的振动信号经预处理后的计算结果，共500组振动信号，后续分析均以A相振动信号为对象进行计算。由图2可见，振动信号呈现出一定的非平稳性特性。

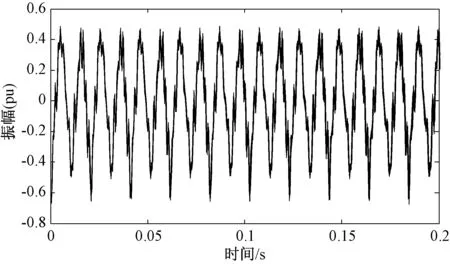
图2 预处理后的振动信号Fig.2 Vibration signals after pretreatment

在对选定的变压器振动监测样本数据进行系统聚类时，需要选取合理的距离递推公式。其中，本文选用的振动信号样本数据为监测系统2个月内的数据，共15000组样本。表1为根据式(2)～式(6)的距离递推公式计算得到的聚类相关系数。由表1可见，采用中间距离法作为合并类之后的递推公式计算得到的聚类相关系数最大，能够使本文的聚类效果达到最优，故本文选取中间距离法进行距离递推计算。

表1 不同递推公式对应的相关系数值Tab.1 Value of cophenetic correlation coefficient corresponding to different recursion formula

图3为计算得到的变压器振动信号在不同聚类个数下类簇总体距离的变化曲线。由图3可知，随着聚类个数的增加，类簇总体距离呈现递减的趋势，并且下降的速度从N=6处开始明显放缓，这表明类簇的大小和形状逐渐趋于稳定。所以，本文选择聚类个数为6。

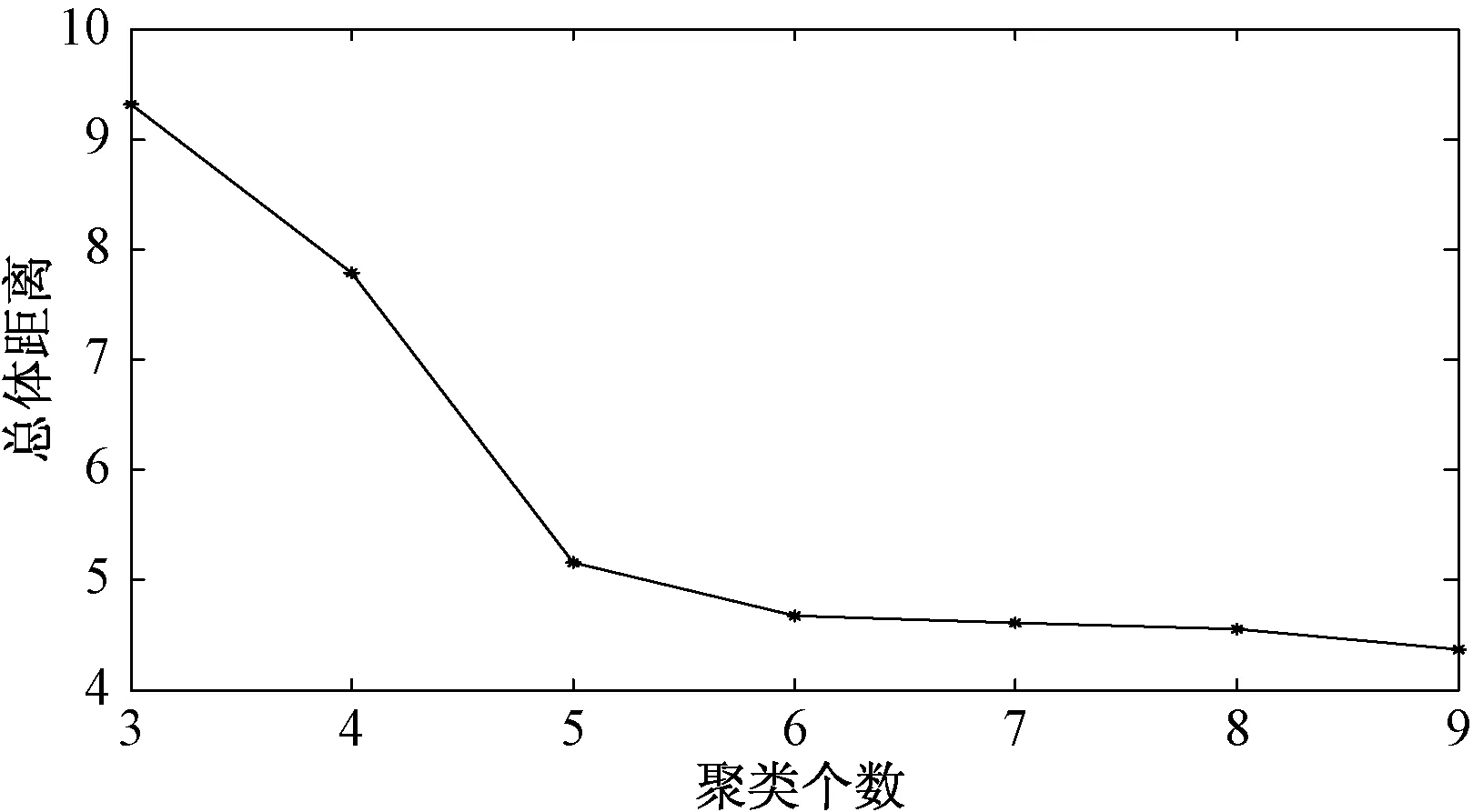
图3 总体距离曲线Fig.3 Curve of total distance

依据设定的聚类个数，对变压器振动监测信号进行了系统聚类，提取得到了每一类簇的变压器振动信号特征曲线，如图4所示。由图4可见，不同变压器振动信号特征曲线之间的区别较为明显，每一条振动特征曲线反映了该类振动信号的振动模式。

为了对变压器绕组状态进行分析评判和验证本文所提系统聚类分析方法的有效性，本文选取聚类样本之外的500kV变压器A相测点的10组变压器振动在线监测信号作为测试样本进行分析。图5为预处理后的振动信号。

分别取显著性水平α=0.05和α=0.01的控制上限作为预警限和报警限，计算各待检测振动信号的T2统计量，绘制T2控制图，如图6所示。

由图6可知，这10组变压器振动在线监测信号的T2统计量均远远低于UCL预警限，表示变压器绕组状态为正常。此外，所选的各组变压器振动信号的T2统计量相对来说较为接近，这在一定程度上也反映了这些振动信号之间具有较高的相似度。因本文所分析的500kV变压器为在运变压器，现场运行状态的综合分析结果也显示其状态为正常。显然，T2控制图的判断结果与实际结果相符，从而验证了本文所提方法的准确性和有效性。

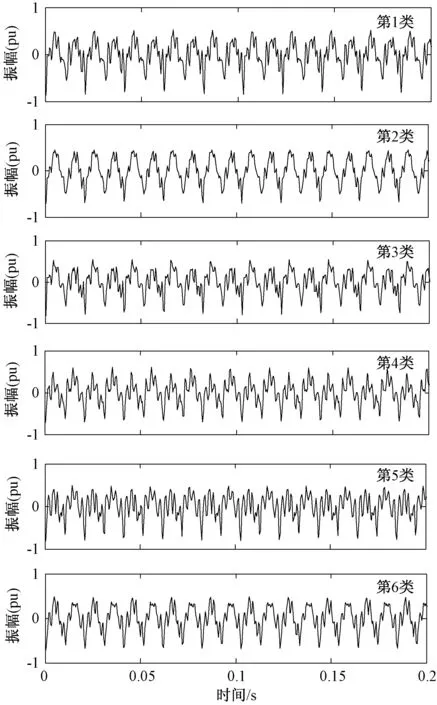
图4 振动特征曲线Fig.4 Vibration characteristic curves

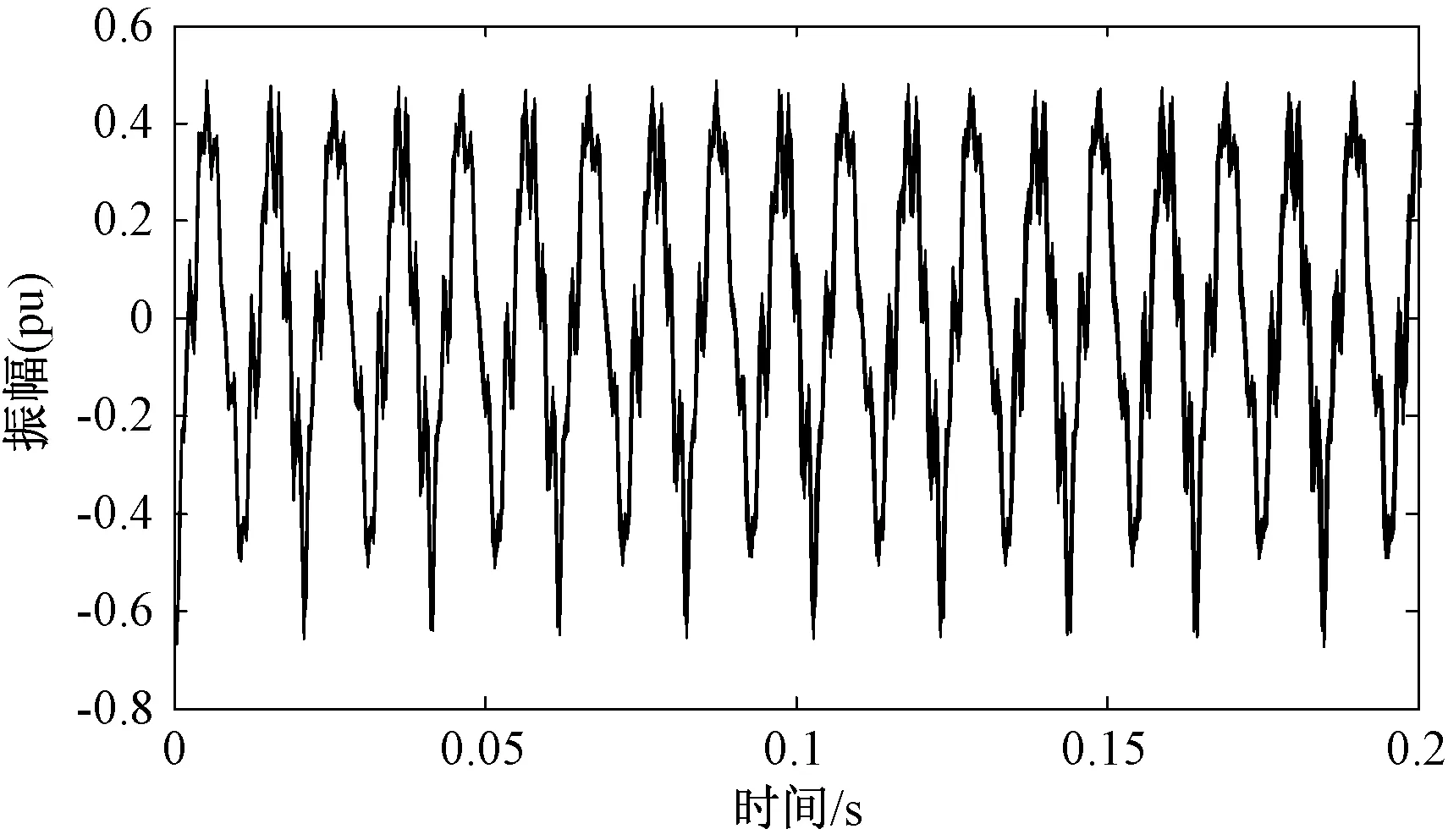
图5 测试样本Fig.5 Vibration signals for testing

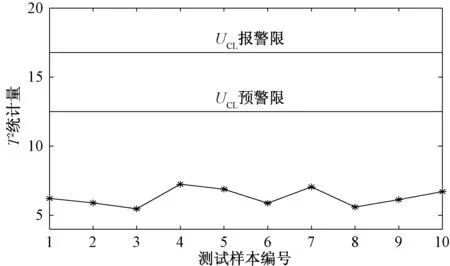
图6 T2控制图Fig.6 T2 control chart

4 结论

基于系统聚类的方法对某500kV变电站变压器振动在线监测系统的海量振动监测信号的分析结果表明：

(1)对变压器振动监测系统中的振动信号进行系统聚类后提取得到的振动信号特征曲线可以反映运行中的变压器振动特征，基于中间距离法的距离递推公式能够使得变压器振动信号的聚类效果达到最优。

(2)T2控制图能够较好地反映在运变压器振动监测信号及绕组状态的过程变化，通过比较振动信号特征曲线的T2统计量与T2控制图中的控制限，可以较为准确地判断变压器的绕组状态，提高变压器的运行可靠性。

(3)本文方法同样适用于其他类型变压器振动信号的特征分析，具体来说，只需对变压器振动在线监测数据进行系统聚类，提取振动信号特征曲线和计算统计振动信号的T2统计量及其控制限即可。