基于广义最小二乘的风力机风速-功率曲线拟合方法研究

韩文卓， 王方雨， 戈志华

(1. 华北电力大学能源动力与机械工程学院， 北京 102206；2. 新能源电力系统国家重点实验室， 华北电力大学， 北京102206)

1 引言

近年来，随着新能源的快速发展，国内风电装机容量持续增加，风电已经成为电力系统重要的电源之一。然而风电电源与传统电源在结构与出力特性上明显不同，风电的波动性和随机性将给电网安全、稳定及经济运行带来诸多不稳定因素[1,2]。为了保证电网的运行安全，风力机、风电场及风电集群建模成为现代电力系统的热点研究内容之一。

目前，风电场以及风电集群建模大多以风力机单机模型为基础，风力机的模型精度将直接影响大型风电场及风电集群模型的精度[3,4]。目前风力机的模型研究主要集中在内部特性及其对电网的影响机理上。文献[5]基于小信号干扰理论建立双馈风力机动态等值模型，该模型包含了16个状态运行变量，具有一定的代表意义；文献[6]比较分析了转速直接求导以及基于转速控制两种风力机动态建模方法，并仿真分析了两种模型的适用性及优缺点；文献[7]基于永磁同步发电机研究风力机的动静态特性，采用基于加速度反馈的动态转矩补偿法实现风力机的动态模拟。这些机理建模研究工作量大，不适合大型风电场建模研究[8-11]。

针对风力机外部特性的研究较少，目前风电场风速-功率特性主要依据厂家提供的风力机标准功率特性曲线，但文献[12,13]指出，标准功率特性曲线的风洞测试环境较为严格，而风力机实际运行具有较大的分散性，与标准曲线并不完全相符，因此模型误差较大。基于此，部分学者开始采用实测风速-功率数据进行外特性研究。文献[14]针对特定发电机组实测运行数据，运用数理统计方法，寻找每一个功率对应的最大风速运行点，并采用三次样条插值理论得到风力机风速-功率运行曲线；文献[15]采用支持向量机聚类算法对风力机进行聚类，求出风力机平均风速及平均功率，采用最小二乘理论对风速-功率运行点进行拟合，得到风力机的风速-功率运行曲线。这些研究为风机外特性建模奠定了良好的基础，但仍然没有考虑风力机的统计特性，存在传统最小二乘拟合算法拟合次数难以确定、数量级拟合范围狭窄且规范方程病态无解等缺点。

针对上述问题，本文首先提出广义最小二乘原理，运用不定秩变解原理解决规范方程可能病态无解的缺点，以自适应原理解决拟合次数固定的缺陷。并基于统计学原理，提出适应于大型风电场静态建模的风力机拟合数据序列产生方法，极大提高了风力机风速-功率模型的收敛性及精确性。

2 广义最小二乘原理分析

传统最小二乘法需要求解Anxn=bn方程组，但该方程存在两个主要缺陷：①该方程可能为不相容的矛盾方程，无解；②拟合次数不能调整。针对上述问题，提出广义最小二乘原理，其主要包含两部分：①不定秩变解原理，解决病态无解问题；②自适应原理，解决拟合次数固定问题。

2.1 不定秩变解原理分析

由文献[16]可知，对于不相容的矛盾方程组，引入广义逆的概念，可分为以下两类进行讨论：

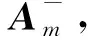
(1)

(2)若rank(A,b)≠rank(A)，即该拟合方程无解，则求取该方程组的最小二乘解，其通解为：

(2)

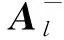
对于一般的矛盾方程组，式(2)的解并不唯一，则求取其极小最小二乘解，其值唯一，计算公式为：

xn=A+b

(3)

式中，A+为极小最小二乘广义逆。

2.2 自适应原理分析

提出自适应次数的概念，针对特定的数据序列，在拟合过程中，自动寻找最佳的拟合次数，保证拟合多项式具有较好的精度。

为了表征拟合效果，首先提出多项式拟合残差指标：

(4)

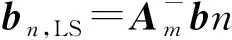
为了使拟合多项式次数朝着残差减小的方向更新，拟合过程中，拟合次数按照下述规则自动更新：

(5)

Y1=‖rnl,LS‖<‖rnl+1,LS‖and‖rnl,LS‖<‖rnl-1,LS‖

Y2=其他

式中，nl为第l次迭代所对应的拟合次数；sgn(·)为符号函数，其定义如下：

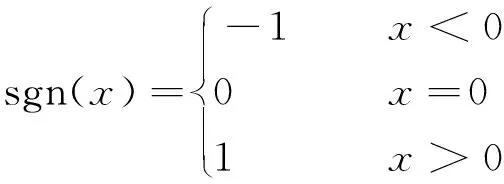
(6)

Snl为迭代步长因子，其值与迭代步长随残差的变化率有关，按照式(7)求取：

(7)

其中，[·]为取整函数，若Snl<1，则令Snl=1；t=‖rnl,LS‖-‖rnl-1,LS‖。

nmin为当前迭代最优拟合次数；nmax为可能的最大拟合次数；α、β为全局变量因子，为防止迭代进入局部最优而设置，其取值规则为：当α=1时，β=0～1；当β=1时，α=0～1。其最佳取值可采用遗传算法进行求取，此处不再赘述。

3 风速-功率拟合数据序列生成方法分析

传统计算风电场输出功率的方法主要依赖于厂家提供的风力机标准功率特性曲线[17]，如图1所示。

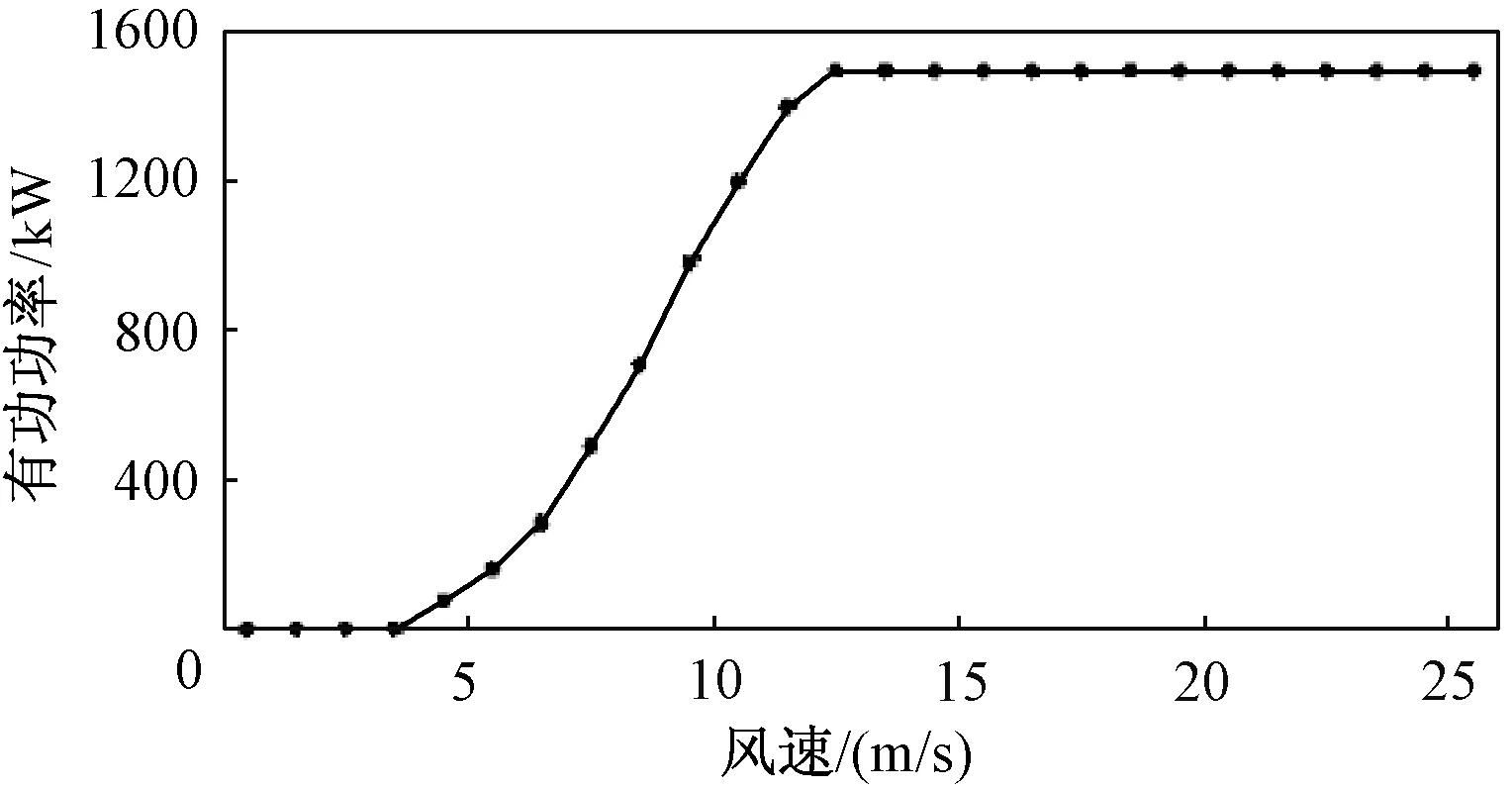
图1 双馈感应式风力机标准功率特性曲线Fig.1 Standard power characteristic curve of doubly fed induction generator

在实际的运行过程中，风力机并不是按照厂家设计的风速-功率特性曲线运行，而是分布在一个较宽的范围内，如图2所示。

图2 双馈感应式风力机实测风速-功率散点图Fig.2 Measured wind speed power scatter diagram of doubly fed induction generator

风力机有功出力与其所受风速有关，若将风力机看作一个二端元件，忽略其内部特性，完全将其看作是一个“黑匣子”，则风力机有功出力可表示为：

P=f(v)

(8)

本文采用概率加权平均值序列法形成待拟合的数据序列，并运用数据重构原理对其进一步处理。

3.1 概率加权平均值序列法

假设共有m台相同型号的风力机，其实测风速-功率散点图如图2所示，不妨设其切入风速为vmin，切出风速为vmax，为了方便测量，将风速从切入风速到切出风速划分为s个等宽的风速区间，则每个风速区间跨度为：

(9)

据此得到风速的区间序列为：

v=[vmin,v2,…,vi,…,vs,vmax]

(10)

式中，vi=vmin+iΔv

进而可得风速的平均值序列为：

vmean=[v1-mean,v2-mean,…,vs-mean]

(11)

式中，vi-mean为第i个区间风速平均值。

在风速区间划分的基础上，按输出有功功率将拟合数据分为等宽的k个区间，则每个功率区间跨度为：

(12)

对于第i个风速区间，其功率加权平均值按照式(13)求取：

(13)

式中，Pi,j-mean为第i个风速区间、第j个功率区间内所有实测数据的功率平均值；gi,j=Ni,j/Ni，为风速在vi-mean下Pi,j-mean出现的概率值；Ni为第i个区间段内实测数据个数；vi,j为第i个区间段内第j个数据所对应的风速；Ni,j为第i个风速区间、第j个功率区间内所有实测数据的个数。

由此可得概率加权数据序列为：

{(v1-mean,P1-wmean),…,(vs-mean,Ps-wmean)}

(14)

由理论分析可知，参与测试风力机台数m越多，风速划分区间数s越多，风速区间内测试数据数Ni越多，所得风速特性曲线越精确。

3.2 数据序列重构分析

由3.1节方法得到的数据序列具有如下特点：①数据数量级分布较宽泛；②数据相对于坐标的基准点极其不对称。鉴于此，为了提高实验数据的拟合程度，减小正规方程组系数矩阵病态程度，需对3.1节的数据序列进行重构，主要步骤如下：

(1)数据平移

根据式(15)进行数据平移，可获得较好的数据范围。

(15)

式中，Θv=min(v)；ΘP=min(P)；E为单位矩阵，其规模为1×s；Δv为风速数据平移误差控制矩阵；ΔP为有功出力数据平移误差控制矩阵。经过数据平移的数据均位于第一象限，且靠近坐标原点中心。

(2)数据转换

根据式(16)进行数据转换，可减小数据动态范围，增强数据拟合稳定性。

(16)

式中，abs(·)为绝对值函数；a为对数底数，根据数据宽松程度进行取值，一般a=10可以满足要求。

(3)数据动态压缩

经过前两步平移和数据转换处理后的数据序列已经初步具备了数据稳定拟合的能力，为了降低最小二乘法中正规方程组的条件数，还需对上述数据进行数据压缩和转换，以便进一步降低数据拟合的病态程度。首先对x方向数据进行对称处理，将vtransfer进行平移，使之关于原点对称，其平移公式为：

(17)

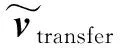
(18)

式中，γ为扩展系数，其值为：

(19)

式中，r为多项式拟合次数。

由式(19)可知，γ值与拟合次数有关，它会随着自适应次数变化动态改变，从而实现动态压缩过程。

4 风力机风速-功率拟合模型建立步骤

根据第3节的分析，给出风力机风速-功率模型建立的详细步骤：

(1)运用概率加权平均值序列法对风力机运行数据进行处理，得到待拟合的初始数据序列{(v1,P1),(v2,P2),…,(vs,Ps)}，并设置自适应初始拟合次数n0。

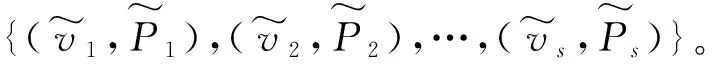
(3)判断拟合方程系数矩阵An0的可逆性，若可逆，求解xn0，转步骤(5)；若不可逆，转步骤(4)。

(4)判断rank(A,b)与rank(A)是否相等，若相等，根据式(1)求解xn0，否则根据式(3)求解xn0。

(5)判断残差是否满足精度要求，即精度是否满足‖rn0,LS‖≤ε，若满足结束迭代，输出结果；否则根据式(13)更新拟合次数nl，转步骤(2)。

(6)若残差精度无法满足‖rn0,LS‖≤ε，设置总迭代次数ltotal，若l>ltotal，则迭代结束，给出残差最小的拟合次数nbest。

5 模型适应性分析

本文所提模型的适应性可从以下方面进行分析：首先从泰勒展开式说明自适应最小二乘自适应次数的合理性，然后针对风力机风速-功率曲线的特点说明该数据重构方法应用于风速-功率建模的适应性，最后以搜索域图说明该方法中不定秩变解原理的正确性。

首先给出泰勒展开式的多项式形式，如式(20)所示：

(20)

式中，O[(x-x0)n]为泰勒公式的余项，是(x-x0)n的高阶无穷小。

由式(20)可知，对于连续非阶跃函数f(x)都可以用多项式pn(a)进行模拟，只要所选取模拟次数nl合理，所得拟合残差‖rn,LS‖就可以达到最小，该方法相对传统定次数的最小二乘拟合方法具有更高的精度优势。实际风力发电机的风速-功率曲线满足连续非阶跃的条件，因此采用自适应最小二乘进行拟合具有很好的精度优势。

此外，由第3节的分析可知，风力机的风速-功率数据具有数量级分布较宽的特点，在采用最小二乘法拟合时，拟合方程可能病态无解。为了说明广义最小二乘数据重构原理在风速-功率建模的高适应性，首先给出数量级分布宽度指标的定义式，如式(21)所示：

(21)

式中，Pi和vi分别为第i个数据点对应的功率和风速；N为数据点总数；MDO为数量级分布宽度指标，其值越大，数量级分布范围越大。

其次，给出最佳拟合次数nbest与数量级分布宽度MDO的变化趋势图，如图3所示。由图3可知，数量级分布范围较小时，最佳拟合次数nbest随MDO的增加缓慢增长，但当MDO较大时，nbest的解变得不稳定，甚至出现无解的情况。本文所提数据重构原理极大压缩了拟合数据的数量级范围，具有很好的可解性。

图3 最佳拟合次数随数量级分布宽度的变化图Fig.3 Variation of number of best fit times with number of orders

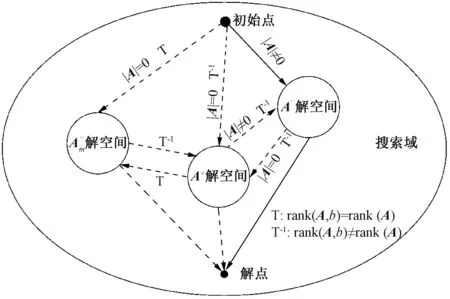
图4 自适应最小二乘解的搜索路径图Fig.4 Search path of adaptive least square solution

6 仿真分析

6.1 仿真环境分析

以我国某风电场风力机的实测数据为例进行分析，场内共有33台风力机，每台机组装机容量为1.5MW。风电场内风力机分布如图5所示。

图5 某实际风电场风力机位置分布图Fig.5 Distribution of wind motor in an actual wind farm

选取2015年6月5日20:00～2015年6月6日8:00的实测数据，采用MATLAB编程进行分析。

6.2 广义最小二乘法适应性仿真验证

目前风力机风速序列常采用最大概率法，为了验证广义最小二乘法针对风力机有功-风速曲线拟合的适应性，首先给出数据重构前后数量级分布宽度指标MDO的变化，如表1所示。由表1可知，数据重构后，MDO值变小，且概率加权平均值序列法本身对数据序列也具有数量级宽度平抑特性。

表1 数据重构前后MDO变化Tab.1 MDO changes before and after data reconstruction

其次给出数据重构前后数据序列拟合残差与拟合次数的关系，如表2所示。由表2可知：

(1)采用数据重构后，数量级分布宽度指标MDO变小，拟合残差‖rn,LS‖数值也随之变小，证明了数据重构针对宽数量级分布范围数据序列的高适应性。

(2)概率加权序列法产生的拟合数据序列拟合残差数值较小，在相同条件下更易收敛。

(3)采用本文算法，部分传统最小二乘病态无解的数据转变为广义可解，提高了算法收敛性。

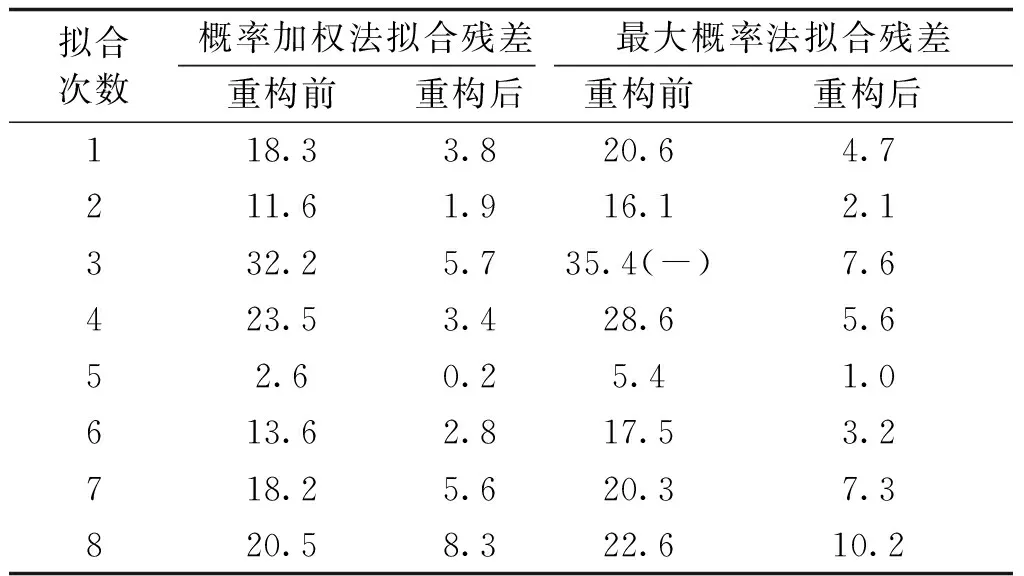
表2 拟合残差与拟合次数的关系Tab.2 Relationship between residual difference and number of fits

注：(-)表示采用传统最小二乘法，系数矩阵不可逆，无解。

最后，为了说明自适应最小二乘法求解时的寻优特性，给出多项式拟合次数随迭代次数的变化关系，如图6所示。由表1和图6可知，该案例中最佳拟合次数为5，且多项式拟合次数会随着迭代次数的增加迅速向最佳拟合次数nbest更替，克服了传统最小二乘拟合次数难以确定的缺陷，证明了广义最小二乘自适应次数的正确性。

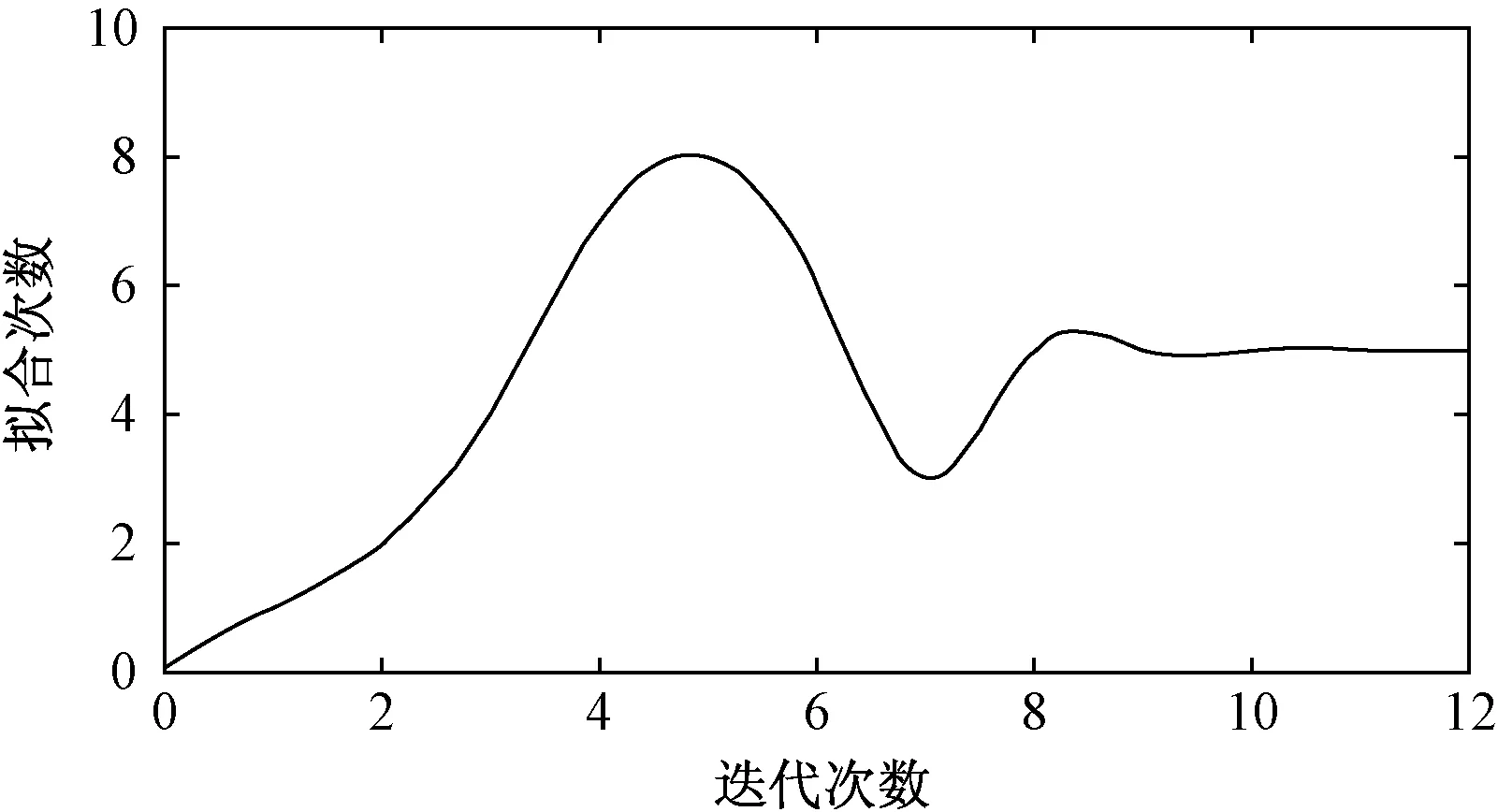
图6 多项式拟合次数随迭代次数变化关系图Fig.6 Relationship between number of polynomial fitting and number of iterations

6.3 风力机风速-功率曲线精确性仿真验证

为了验证风力机风速-功率曲线精确性，以及相对传统方法的优势，从本文所提拟合数据序列产生方法及广义最小二乘两个角度出发构造以下两种仿真方案：

(1)方案一(传统方法)：采用传统最大概率法生成风速序列，采用传统最小二乘法拟合。

(2)方案二(本文算法)：采用概率加权法生成风速序列，采用广义最小二乘法拟合。

采用两种不同方案生成的风速-功率曲线对风力机有功出力进行计算，与实际数据进行比较。风速变化特性如图7所示。

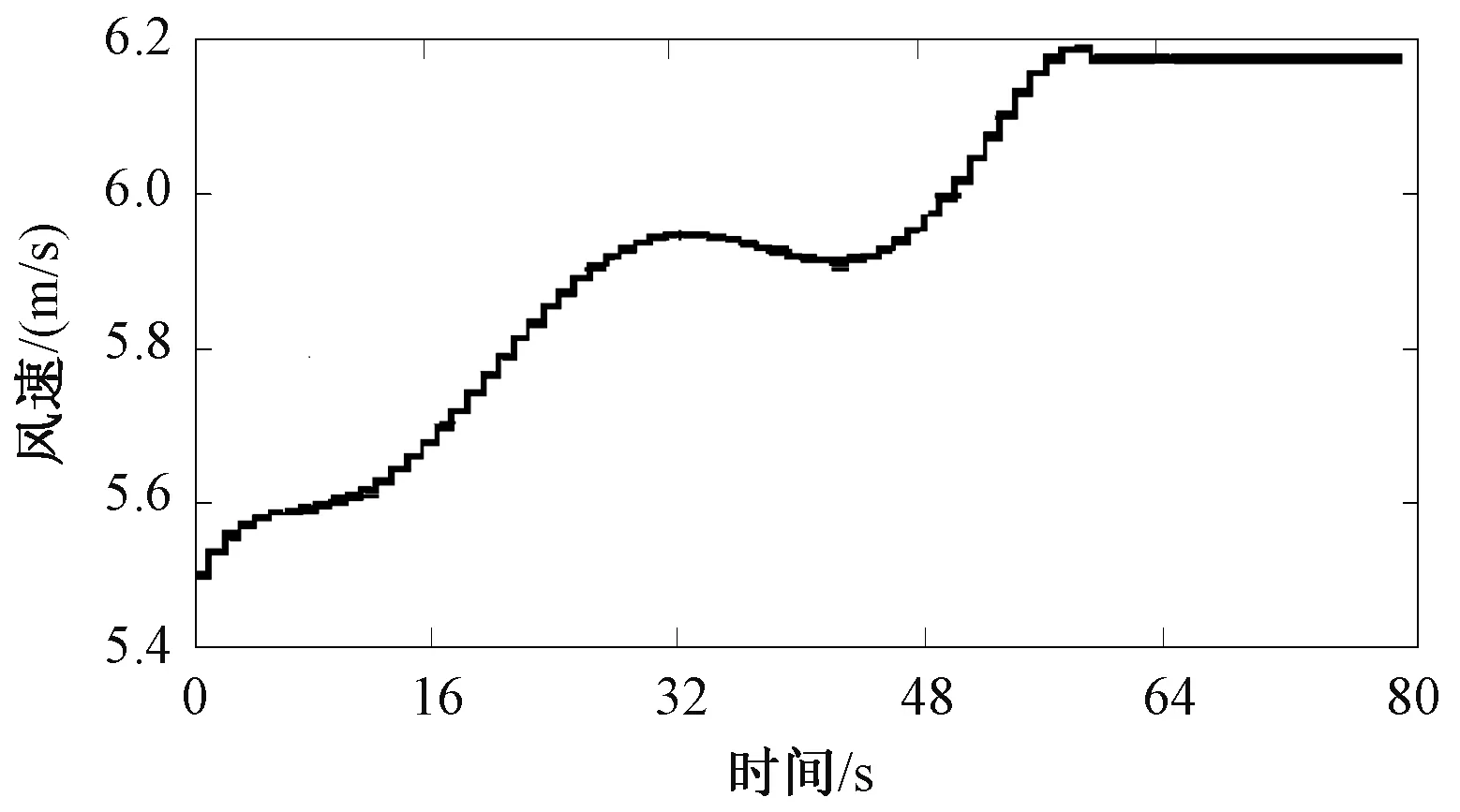
图7 风力机风速变化曲线图Fig.7 Wind speed variation curve of wind turbine

图8和图9分别为采用传统风速-功率曲线以及本文所提风速-功率曲线的计算结果。其中Pm为风力机有功功率参考值，Pout为风力机模型输出的有功功率，Preal为实测的风力机输出功率。在控制器的作用下Pout对Pm进行追踪。

图8 采用传统方法的仿真计算结果Fig.8 Simulation results using traditional methods

图9 采用本文方法的仿真计算结果Fig.9 Simulation results using method of this paper

由图8和图9可知，采用传统风速功率曲线计算结果与实测数值存在约60kW的误差，误差率超过30%，计算结果精度较差；采用本文所提方法可以很好模拟风力机有功出力，证明了概率序列拟合数据生成方法以及广义最小二乘拟合的精确性。

7 结论

本文针对传统最小二乘法的固有缺陷，提出基于广义最小二乘的风力机风速-功率曲线拟合模型，经过理论及仿真验证得到如下结论：

(1)概率加权序列法产生的拟合数据序列本身具有数量级宽度平抑特性，且拟合曲线最能体现风力机出力波动特性及分散特性，模拟效果最好。

(2)经过数据重构，可以明显压缩数量级分布范围，提高拟合精度和收敛性。

(3)采用自适应原理的广义最小二乘法可以迅速找到最佳拟合次数，并且引入广义逆极大增加了解域空间，保证算法可解。

(4)采用自适应原理可以快速得到数据最佳拟合次数，保证算法的高精确性。

本文研究为大型风电场及集群等效聚合模型研究奠定了良好的基础。