考虑光伏和电动汽车不确定性的配电网鲁棒经济调度

卢 艺， 梁俊文， 程韧俐， 卢 苑， 林舜江， 刘明波

(1. 深圳供电局有限公司电力调度控制中心， 广东 深圳 518001；2. 华南理工大学电力学院， 广东 广州 510640)

1 引言

随着新能源技术的不断发展，以光伏为代表的可再生能源发电和电动汽车负荷接入配电网的容量不断增加，其注入功率的随机波动使得配电网的运行调度面临着新的挑战[1,2]。光照强度、环境温度和阴晴雨雾等气象条件决定了光伏电站出力的不确定性较大，电动汽车用户的出行特性和行驶里程也使得电动汽车充电站负荷功率具有较大的随机性。因此，配电网运行中面临的不确定性日益增强，运行风险日益增大。传统的确定性优化调度方法已不能满足配电网实际发展的需要，必须采用不确定性方法对配电网优化调度问题进行建模和求解。

在电力系统优化运行调度中，为了考虑间歇性能源出力及随机负荷的不确定波动特性，常使用随机规划、场景法和模糊规划等不确定性优化方法。文献[3,4]通过概率密度函数分析和随机模拟结合的方式考虑配电网中间歇性能源出力等不确定性因素，建立机会约束规划模型。文献[5,6]基于场景法考虑间歇性能源随机特性建立了含风电电力系统经济调度模型；但机会约束规划和场景法都需要事先知道不确定变量的概率分布函数，这需要通过对大量的历史数据进行统计计算才能获得准确的概率分布函数。文献[7,8]采用模糊规划考虑优化问题中的不确定因素，将不确定性表示为模糊变量，约束条件表示为模糊集合，并且用模糊隶属度表征约束条件的满意程度。但是，模糊规划中不确定隶属度函数的确定依赖于有限的样本数据和决策者的经验，容易造成结果误差。相比于上述方法，鲁棒优化方法以不确定集的形式描述问题中的不确定性，通过优化方法得到不确定变量在极端场景下的目标函数最优的系统调度方案。它与随机规划不同，不需要知道不确定变量的概率分布，只需要知道不确定变量分布的区间范围，具有较好泛化性，近年来在含不确定变量的电力系统优化问题研究中受到广泛关注[9-13]。文献[9]考虑可再生能源的随机特性，构建了计及可再生能源、储能和冷热电联产系统的微电网经济运行鲁棒优化模型。文献[10]以椭球不确定集描述风电场的不确定性，建立了基于椭球鲁棒优化理论的风电场出力最大且满足安全约束的优化模型。文献[11]建立了考虑可再生能源不确定性微电网能量优化鲁棒模型。文献[12]针对高渗透率的风电、光伏等新能源并网的微电网调度问题，建立了基于不确定集优化的鲁棒经济调度模型。文献[13]利用解的鲁棒性可控的鲁棒优化方法，以微电网内发用电成本最低为目标，建立了含风电的工业微电网经济调度模型。然而，文献[9-13]的鲁棒优化方法主要研究微电网优化调度问题，较少应用于配电网优化调度中；并且，这些文献只涉及微电网调度中的发电与负荷的功率平衡问题，没有考虑供电网络运行的功率损耗，且没有考虑供电网络运行的安全约束。

鉴于此，本文针对考虑光伏电站出力和电动汽车充电站负荷不确定波动的配电网优化调度问题，利用鲁棒优化的方法，以可控发电机组出力和储能充放电功率为决策变量，定义使得网络损耗费用最大的不确定变量集中的元素为极端场景，以极端场景下配电网运行总成本最小为目标函数，建立了含光伏和电动汽车的配电网鲁棒经济调度模型。并且运用Benders分解算法将Min-Max问题分解为主问题和子问题进行交替迭代求解，快速得到鲁棒优化调度方案。

2 光伏电源和电动汽车充电负荷特性

2.1 光伏电源特性

光伏电源是利用光伏效应将太阳能转化为电能的装置，其输出功率和光照强度、环境温度和阴晴雨雾等气象条件密切相关，可由温度和光照强度表达[12]，如式(1)所示：

(1)

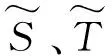
2.2 电动汽车充电负荷特性

电动汽车的充电行为具有随机性和分散性，要获得电动汽车充电站的负荷特性，可运用历史数据对电动汽车的出行规律进行统计分析得到电动汽车的行驶特性，然后采用蒙特卡洛仿真方法求得单台电动汽车充电功率需求，进而计算出多台电动汽车的总体功率需求。电动汽车充电站负荷主要受到电动汽车的行驶特性影响，如用户出行和返回时间以及日行驶里程等。根据2009年美国交通部对全美家用车辆出行统计分析的结果[14]，车辆的返回时刻(即充电起始时刻)满足正态分布，如式(2)所示，日行驶里程满足对数正态分布，如式(3)所示[15]。

(2)

(3)

式中，t为车辆的充电起始时刻；us=17.47，为充电起始时刻的均值；σs=3.41，为充电起始时刻的标准差，代表充电起始时刻分布的离散程度；x为车辆的日行驶里程；uD=2.98，为日行驶里程的对数均值；σD=1.14，为日行驶里程的对数标准差，代表行驶里程分布的离散程度。

假设电动汽车每次出行结束时刻即开始充电，每次充电都充满，充电过程近似于恒功率特性，则根据电动汽车的每千米耗电量及行驶日里程，可得到电动汽车的充电时长，如式(4)所示：

Tc=DW/Pev0

(4)

式中，Tc为充电时长；D为日行驶历程；W为每千米耗电量；Pev0为电动汽车的额定充电功率，取3kW。

假设电动汽车充电起始时刻和日行驶历程相互独立，根据式(2)～式(4)，通过蒙特卡洛模拟仿真，可以得到充电站在不同电动汽车规模下自由充电一天的充电负荷功率预测曲线，如图1所示。在一定电动汽车规模下，通过足够多次蒙特卡洛模拟仿真(如500次)，可得到该充电站在此电动汽车规模下的多条负荷功率预测曲线，由此可以估计充电站在此电动汽车规模下各时段充电负荷功率的期望值和波动范围。

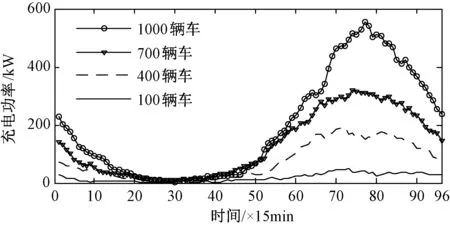
图1 充电站在不同汽车规模下的充电负荷曲线Fig.1 Load curves of charging station with different number of electric vehicles

3 配电网鲁棒经济调度模型

含光伏和电动汽车的配电网经济调度问题中涉及到光伏电站出力、电动汽车充电负荷功率等不确定因素，本文以鲁棒优化的思想考虑不确定因素，建立配电网鲁棒经济调度模型。该模型以配电网网络损耗最大对应的不确定变量取值为极端场景，通过安排可控发电机组和蓄电池的出力使得配电网在不确定变量的极端场景下的总运行成本最小，且满足系统安全约束和设备运行约束。

3.1 目标函数

(5)

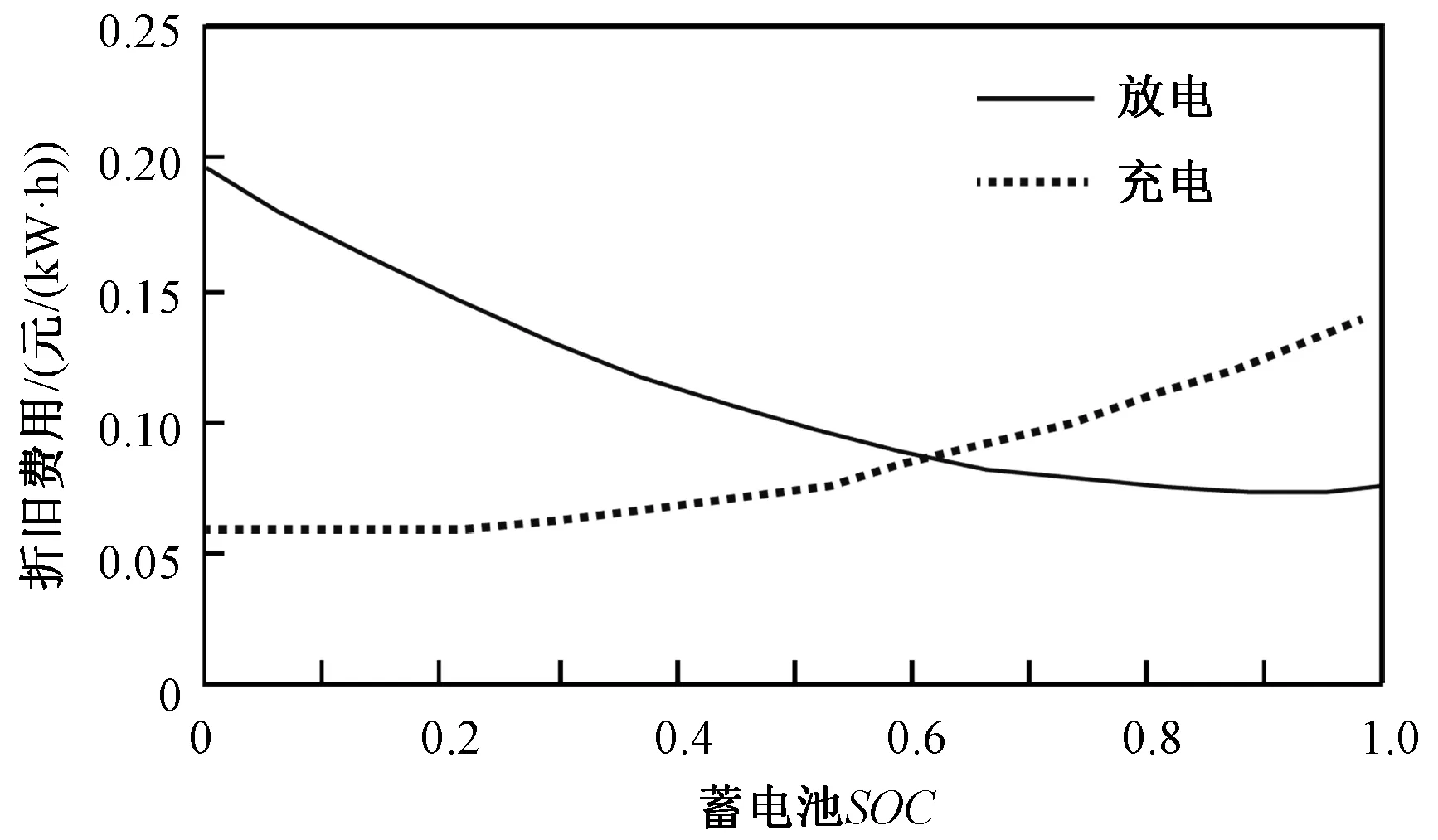
图2 蓄电池充放电系数σ曲线Fig.2 Curves of coefficient σ for battery charge and discharge

3.2 约束条件

(1)功率平衡约束。各个节点的功率平衡约束如式(6)所示：

(6)

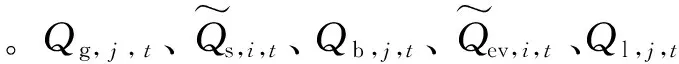
(2)系统运行安全约束。为保证配电网的安全运行，配电线路的传输功率不能超过线路本身的载流量，各节点的电压偏差不能超过安全允许范围，如式(7)所示：

(7)

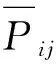
(3)配电网关口注入功率约束。为抑制配电网功率波动对上层输电网的影响，需将配电网根节点的关口注入功率控制在某一范围内，如式(8)所示：

(8)

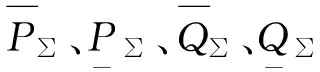
(4)可控发电机组约束。包括输出功率的上下限约束和爬坡约束，如式(9)所示：

(9)

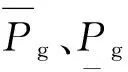
(5)蓄电池储能约束。为了平抑配电网中光伏电站和电动汽车充电站功率的不确定波动，引入蓄电池储能装置，其模型约束包括最大充放电功率约束、储能装置荷电状态约束、运行状态互补约束。运行状态互补约束指蓄电池在实际运行中每个时段t只能处于充电或者放电的其中一种状态。

(10)

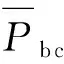
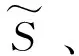
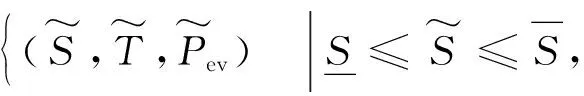
(11)

4 Benders分解法求解鲁棒优化模型

求解配电网鲁棒经济调度模型的关键在于：①如何在不确定变量集合中，找到1组不确定变量值，与最大化网络损耗费用的极端场景相对应；②如何在决策变量集合中，找到1组决策变量值，使得在不确定变量的任意取值下该组决策变量都能够满足优化模型中的约束条件，且使得在极端场景下对应的目标函数最小。

本文采用Benders分解法求解配电网鲁棒经济调度模型[17]。Benders分解法的主要思想为将Min-Max优化问题分解为内外两层问题交替求解，在确定内层解/外层解的情况下求解相应的外层解/内层解，并循环迭代，其中由固定内层解求解外层解的过程中根据内层解的性质加入极点约束或极线约束到外层主问题，由此得到收敛的最优解。按照Benders分解法的思想，可将本文的Min-Max结构优化模型分解为主问题和子问题两部分。子问题寻找使得系统网损费用最大的不确定变量极端场景；主问题则针对极端场景，求解使得系统运行总成本最小的可控发电机组出力和蓄电池出力。子问题和主问题分别描述如下。

4.1 子问题

(12)

式中，z1为求解过程中构造出的辅助变量。

约束条件包含式(1)、式(6)、式(11)。在子问题中，不确定变量作为未知变量，决策变量(Pg,j,t，Pc,j,t，Pd,j,t)为已知量。求解子问题得到最优解后，向主问题约束条件中增加一个最优割集，如式(13)所示：

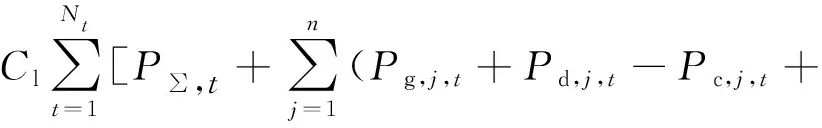
(13)

4.2 主问题

主问题的目标函数为在不确定变量处于极端场景情况下，配电网总运行成本最小，如式(14)所示：

(14)

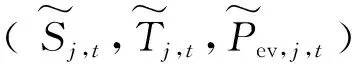
4.3 Benders分解法的计算过程

采用Benders分解法求解配电网鲁棒经济调度模型的流程如图3所示。具体步骤如下。

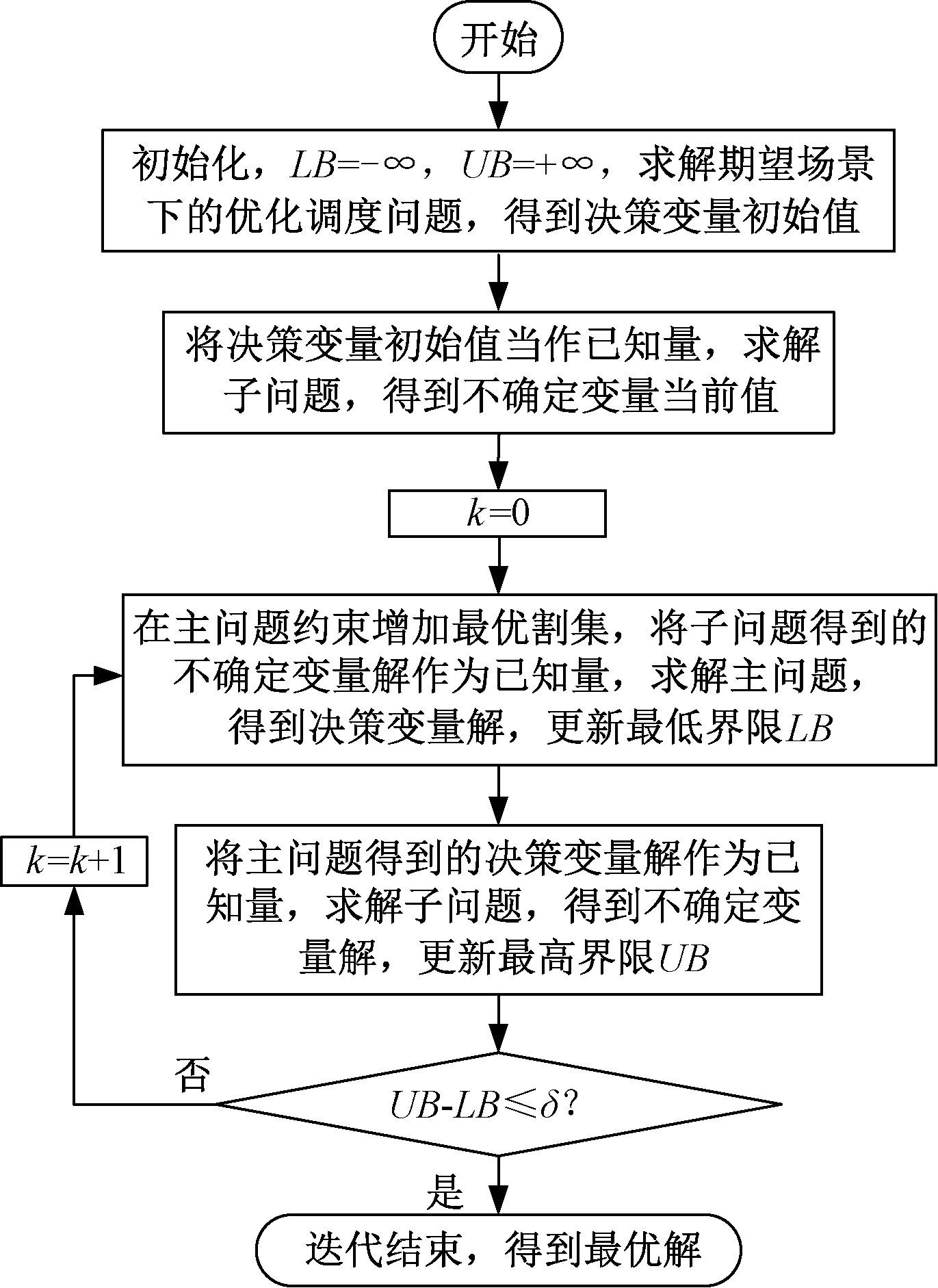
图3 Benders分解算法流程图Fig.3 Flowchart of Benders decomposition algorithm

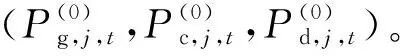
(15)

(16)

(5)当UB-LB≤δ，则迭代结束，输出最优解；否则，令k=k+1，返回步骤(3)。

5 算例分析

算例分析采用IEEE33节点系统，如图4所示。系统包含节点8和节点30的两台可控发电机组，节点15的储能装置，节点16和节点22的两个光伏电站，节点12和节点28的两个电动汽车充电站，车辆的规模各为700辆。可控发电机组的最大出力为600kW，最小出力为0，爬坡和滑坡速率为200kW/h，发电成本系数bg为0.66元/(kW·h)；节点15储能最大充电和放电功率为200kW，容量为800kW·h。光伏、储能及电动汽车的无功功率均以恒功率因数控制，功率因数为0.95。节点1为平衡节点，电压为12.66kV，相角为0°；关口注入有功上下限分别为3200kW和2000kW，注入无功上下限分别为2500kVar和1000kVar，主网购电单价C0采用分时电价，如图5所示[13]。单位网损费用Cl为0.68元/(kW·h)。该地区光伏电站典型日的温度和光照强度的变化曲线分别如图6和图7所示。各个负荷功率按照96点归一化日负荷曲线变化，如图8所示，其中第68时段负荷1.0pu对应于系统中原来的负荷值，并且各时段负荷功率因数都保持不变。电压安全限制的上下限设置为1.06pu和0.94pu。Benders分解法中收敛判据常数δ为10-5。所采用的计算机为Intel(R) Xeon(R) CPU E3-1270 v3 @ 3.50GHz，16GB内存。采用GAMS软件中的CONOPT求解器求解主问题和子问题的非线性规划模型[18]。

图4 IEEE33节点配电网系统Fig.4 IEEE 33-bus distribution system

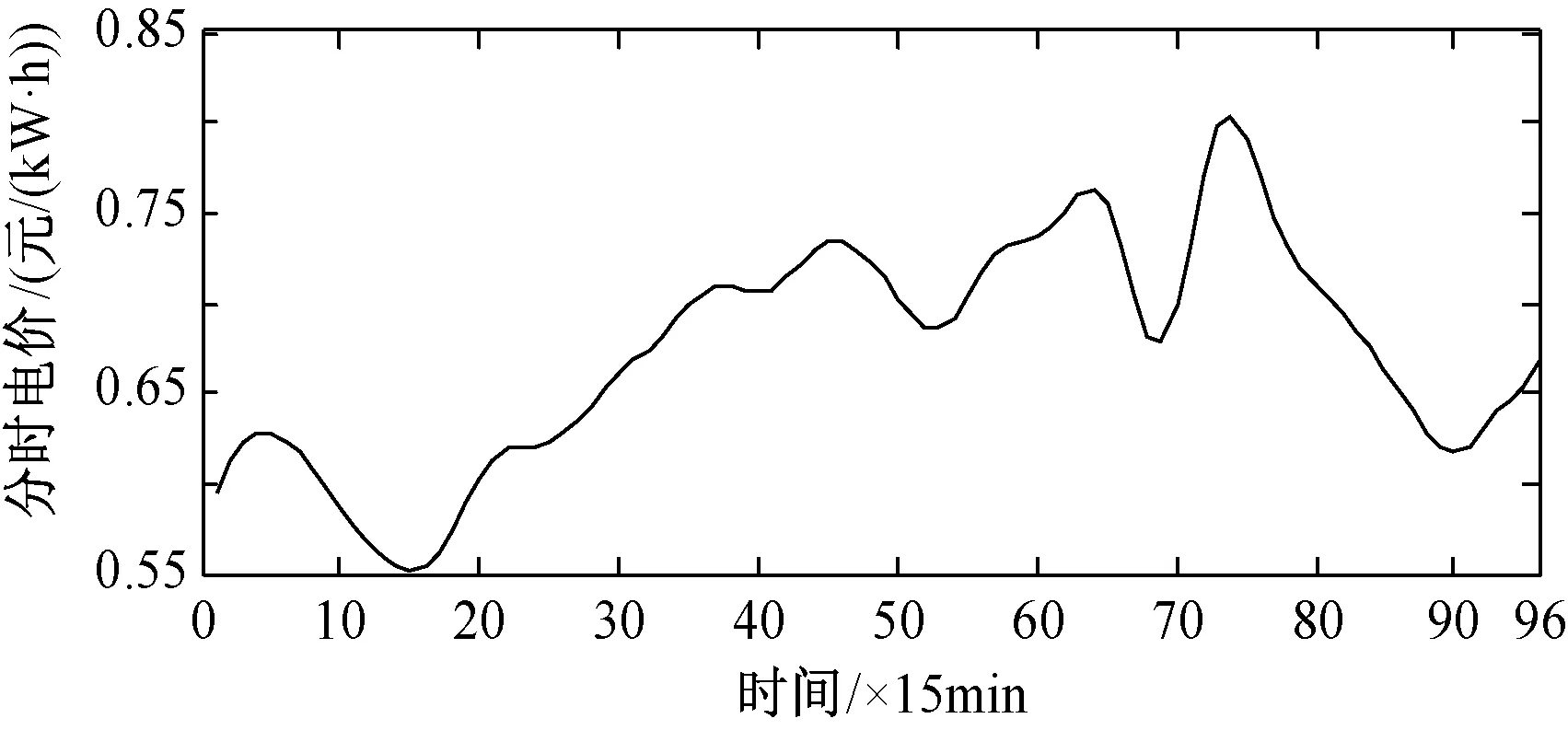
图5 分时电价Fig.5 Time varying factor of electric purchasing

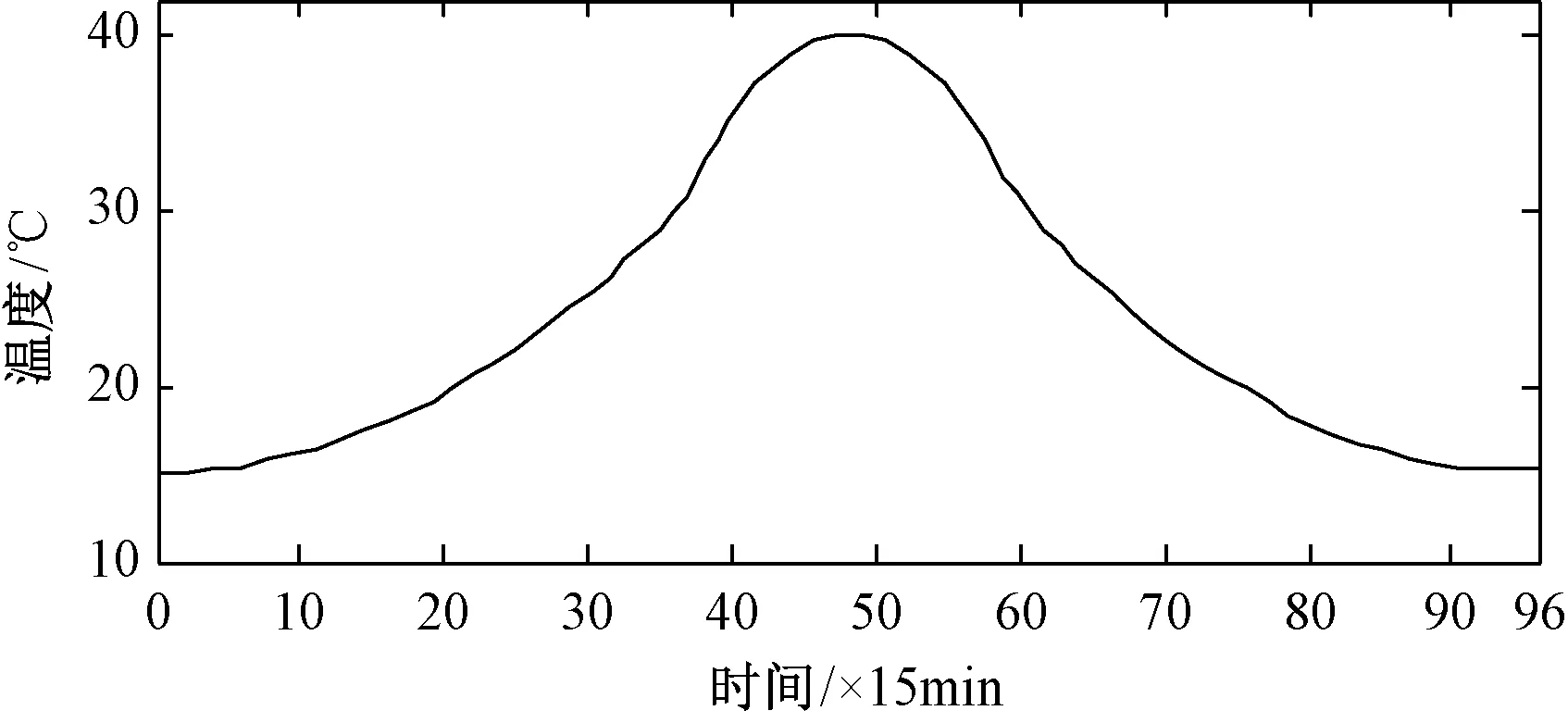
图6 光伏电站典型日的温度变化曲线Fig.6 Typical day temperature curve of photovoltaic power station

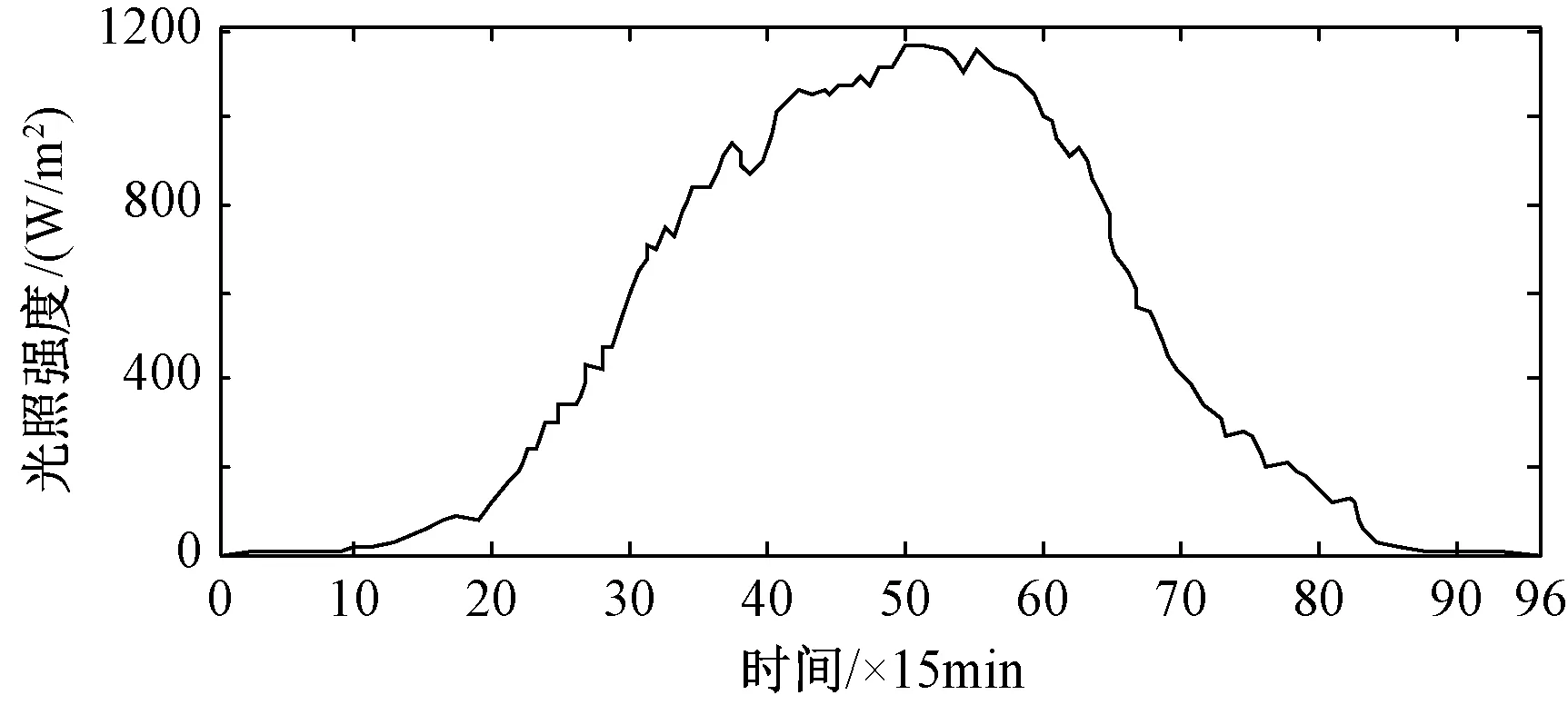
图7 光伏电站典型日的光照强度变化曲线Fig.7 Typical day light intensity curve of photovoltaic power station

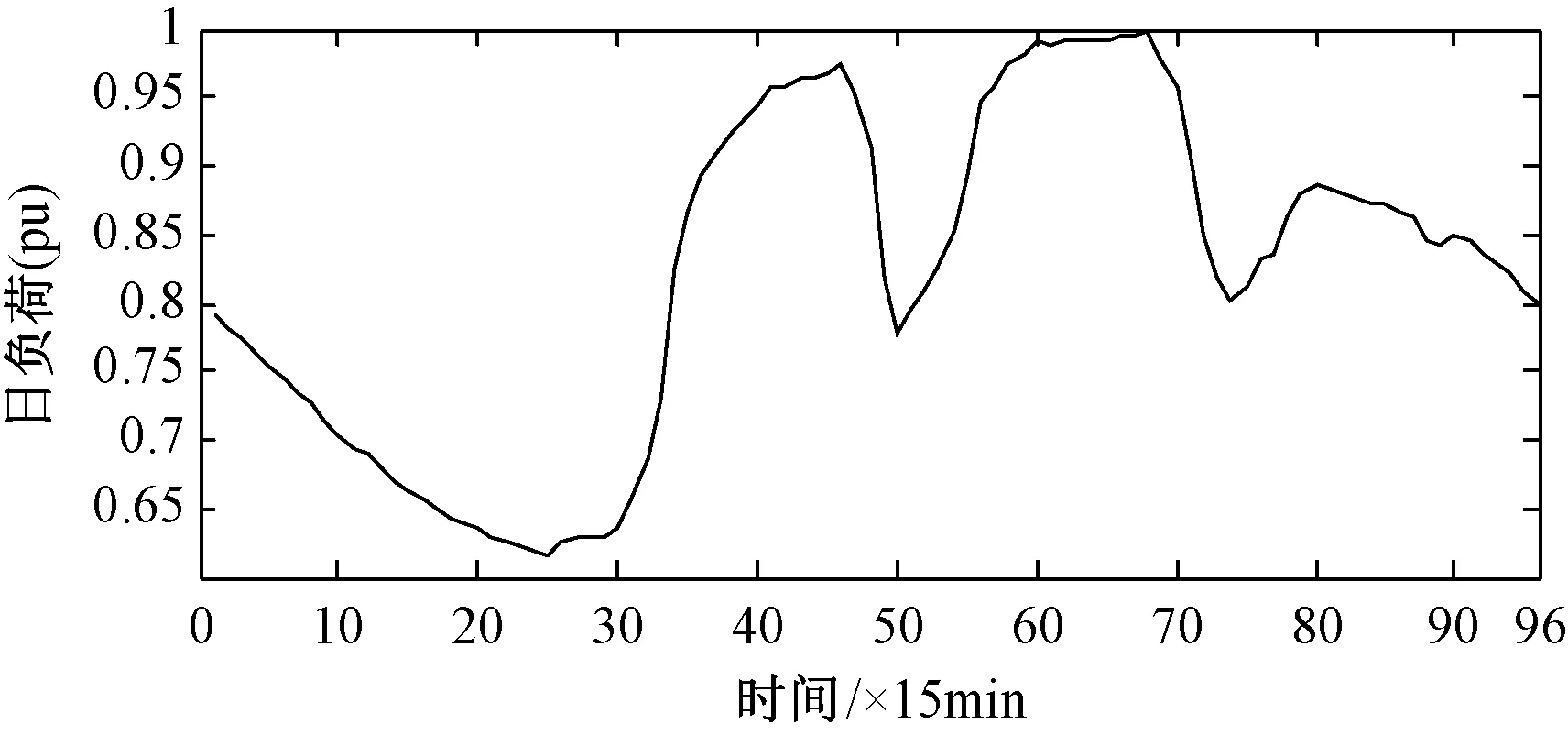
图8 归一化日负荷变化曲线Fig.8 Normalized daily load curve

为了验证本文鲁棒经济调度模型的正确有效性，与确定性优化调度和场景法优化调度进行对比。在确定性优化调度中，光伏电站的光照强度和温度及电动汽车充电站的负荷都为期望值，目标函数为配电网总的运行成本最小。场景法优化调度中，光伏电站的光照强度和温度及充电站负荷的误差场景设定为一系列误差范围在期望值±20%以内的场景，目标函数与确定性优化相同。鲁棒经济调度中，假定不确定变量集合的波动范围为期望值的±20%。三种方法优化得到的结果对比如表1所示。

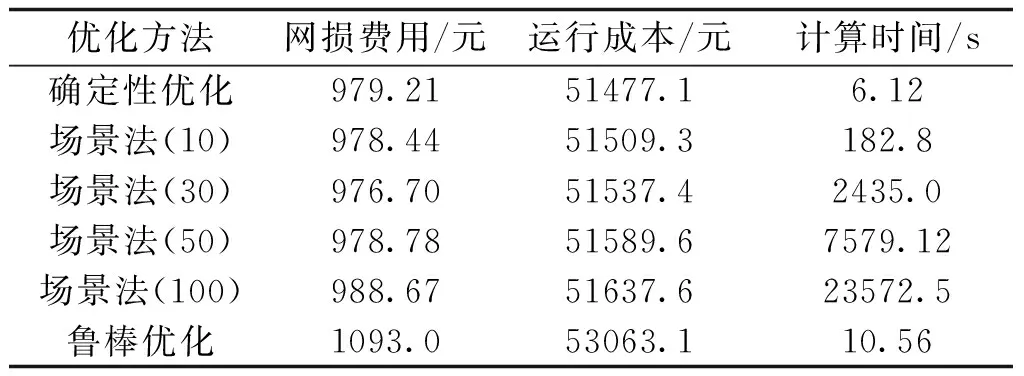
表1 不同方法优化结果对比Tab.1 Comparison of optimization results of different methods

注：场景法括号中的数字表示误差场景数。

由表1可知，鲁棒优化得到的网损费用为1093.0元，比确定性优化得到的网损费用979.21元大，也比场景法优化得到的网损费用大，因为鲁棒优化是寻找对应于网损费用最大的极端场景下总运行成本最小的调度方案。同时，鲁棒优化得到的运行总成本为53063.1元，比确定性优化得到的系统总运行成本51477.1元大，也比场景法优化得到的总运行成本大，这是因为鲁棒优化求解得到的调度方案在光伏出力、电动汽车充电站负荷不确定集范围内的任何取值情况下都满足约束条件，保守性大。另外，当场景法中误差场景的数目越多，得到的总运行成本就越接近鲁棒优化的总运行成本。因为场景法通过误差场景描述光伏出力和电动汽车充电站负荷的不确定性，误差场景越多越容易出现比较恶劣的场景。当场景法中的场景数目取得足够多时，相当于在不确定变量集合中寻找优化调度结果，其结果应该满足这个集合所有可能取值下的约束。而鲁棒优化则是寻找不确定变量集合中极端场景下目标函数最优的结果，同时保证结果满足这个集合所有可能取值下的约束。这时抽样足够多的场景法和鲁棒优化方法的核心思想一致，因此它们的结果会接近。

对比三种方法的计算时间可知，确定性优化的计算时间最短，鲁棒优化计算时间较长，场景法的计算时间最长。确定性优化的只有单个期望值场景约束，场景法优化包含期望值场景和多个描述不确定变量的误差场景约束，随着误差场景数目的增多，需要满足的约束成倍增长，计算量急剧增大，计算时间也快速增长。鲁棒优化用集合的方法描述不确定变量，首先寻找在不确定变量集合中极端场景下目标函数最优的解，在交替求解过程中的每一步其约束条件只涉及到单个极端场景，约束条件较场景法大大减少，因此鲁棒优化的计算时间比场景法明显减少，计算效率大大提高。

鲁棒优化调度方案与确定性优化调度方案对比如图9～图11所示。其中，图9为发电机组的计划曲线，图10为储能装置的计划曲线，图11为关口出力变化曲线。可见，两种方法得到的优化调度方案的变化趋势基本一致。鲁棒经济调度得到的发电机出力、储能出力和配电网关口出力在负荷高峰时期(时段60～96)比确定性经济调度要大，以应对网损费用最大的极端场景，使得鲁棒经济调度方案的总运行成本最高，验证了本文的鲁棒经济调度结果的正确性。

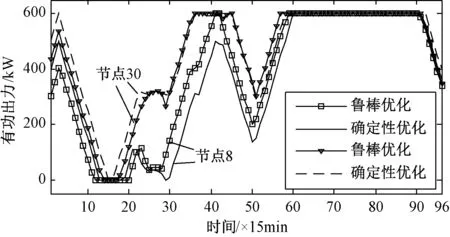
图9 节点8和节点30发电机出力计划曲线对比Fig.9 Comparison of planed real power of generator in bus 8 and bus 30 between different methods

图10 节点15蓄电池出力计划曲线对比Fig.10 Comparison of planed real power of storage battery in bus 15 between different methods

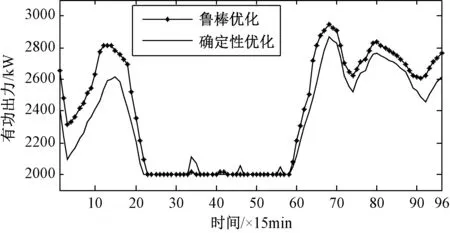
图11 节点1配电网关口注入功率曲线对比Fig.11 Comparison of real power of transformer in bus 1 between different methods

对比在极端场景下，确定性经济调度和鲁棒经济调度方案所得到的电压最低点即节点18的电压，如图12所示。可见，当系统因为光伏电站出力和电动汽车充电站负荷波动出现极端场景时，确定性优化调度在负荷高峰期不能保证系统的电压满足电压安全限制，存在节点电压越下限的情况，危及系统的安全运行；而鲁棒经济调度则能保证系统运行的每一个时段都满足电压安全约束，证明了本文方法获得的调度方案对于光伏电站出力和电动汽车充电站负荷波动的鲁棒性。另一方面，在极端场景下确定性调度方案对应的总运行成本为53108.1元，比鲁棒经济调度的总运行成本53063.1元要大，符合鲁棒经济调度最小化极端场景下的总运行成本的要求。

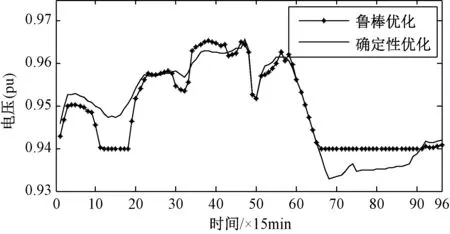
图12 极端场景下不同优化调度方案节点18电压对比Fig.12 Comparison of voltage of bus 18 between different methods

6 结论

本文考虑了光伏电站出力和电动汽车充电站负荷的不确定性，建立了配电网鲁棒经济调度模型。通过算例分析得到以下结论：

(1)运用Benders分解算法将Min-Max鲁棒经济调度问题分解为主问题和子问题的交替迭代求解，得到了对应于网络损耗费用最大极端场景下的鲁棒经济调度方案。

(2)通过与确定性优化调度对比验证了本文鲁棒经济调度模型求解结果的正确性，通过与场景法优化对比，验证了鲁棒经济调度方法比场景法经济调度在计算时间上的高效性。

(3)在光伏出力及电动汽车波动的极端场景下，对比了确定性优化调度和鲁棒优化调度所得到的系统电压，结果表明鲁棒经济调度能够在极端场景下满足电压安全，而确定性优化方案则无法满足。验证了本文鲁棒经济调度模型对光伏和电动汽车功率等不确定性变量的波动具有鲁棒性。