基于改进KH算法优化ELM的目标威胁估计

傅蔚阳，刘以安，薛松

严格来讲，目标威胁估计是一个NP困难问题[1]。在进行威胁估计时，给出一个各种因素与威胁程度的函数关系困难很大。文献[2]使用BP神经网络处理目标威胁估计问题获得了不错的结果，但BP神经网络也有着明显缺点，比如训练时间长、易陷入局部极值、学习率η选择敏感等。所以本文提出了改进的磷虾群算法(oppositionbased learning Krill Herd optimization, OKH)优化极限学习机的目标威胁估计模型。磷虾群算法是2012年由Gandomi等[3]提出的一种新的仿生优化算法。由于其参数少、模型简单、算法性能好而获得大量运用。但是在处理复杂的优化问题时，其易陷入局部极值和出现算法后期收敛速度变慢的问题[4]。极限学习机[5-6]是一种针对单隐含层前馈神经网络(single-hidden layer feedforward neural netwark, SLFN)的算法。该算法与传统训练方法相比，具有学习速度快、泛化性能好的优点，但对初始权值与阈值过度依赖[7]。为解决上述缺点，本文提出了OKH算法，利用收集到的目标威胁度数据建立了目标威胁估计模型 (extrem learning machine，ELM) ，并使用反向磷虾群算法优化ELM模型的初始参数。为了验证本模型的可靠性，将本模型与其他几种神经网络模型作了对比研究。

1 反向磷虾群算法

1.1 标准磷虾群算法

KH算法是基于自然界磷虾群寻找食物和相互通信的模拟，采用拉格朗日模型模拟磷虾的移动且引入了遗传算子来提高物种多样性[8-9]。在KH算法中，每个磷虾都代表了n维解空间中的一个潜在解，磷虾食物代表了算法寻优需要找到的全局最优解。与其他仿生算法相比，磷虾群算法实现起来较为容易，除了时间间隔依据需求人为设定，剩余参数都取自真实生态的研究结果，所以有效避免了因参数设置不当而导致的算法性能下降问题[10]。该算法具体流程如下。

1)磷虾个体的速度更新公式为

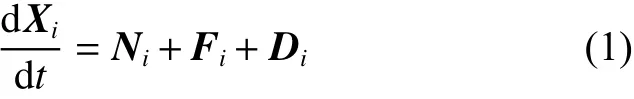
式中：Xi为磷虾的状态；Ni为受诱导运动的速度矢量；Fi为觅食行为的速度矢量；Di为随机扰动的速度矢量；下标i表示第i只磷虾。

2)受诱导运动：

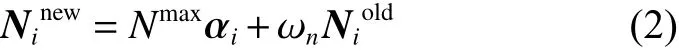
3)觅食行为：

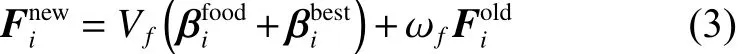
式中：Finew表示觅食行为产生的速度矢量；Vf是觅食速度，一般取0.02 m/s；ωf(0,1)是觅食行为的惯性权重；βifood是食物的吸引力；βibest是从迭代开始到当前时刻个体i的最优状态；Fiold是上一次觅食行为产生的速度矢量。

4)随机扰动：

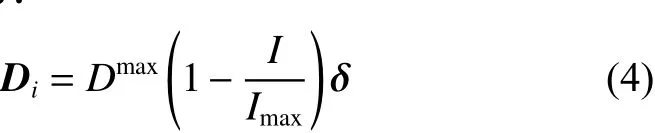
式中：Dmax∈[0.002，0.010] m/s是最大扰动速度；δ为每个变量服从(–1，1)均匀分布的方向矢量。

5)状态更新：

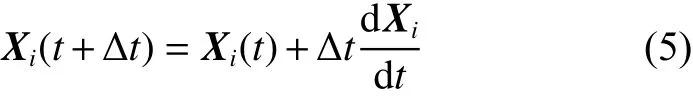
式中： Δ t为时间间隔，必须根据实际问题进行选择。

最后，重复进行受诱导运动、觅食行为、随机扰动，直到满足最大迭代次数后寻优停止。

1.2 改进的磷虾群算法

研究可以发现，对于标准磷虾群算法，随着迭代次数的不断增加，所有磷虾个体都朝同方向运动，使得磷虾群趋同性变得严重[11-12]。本文采用反向学习策略[13-14]对标准磷虾群算法的初始种群与迭代后的种群进行改进，成功改善了磷虾个体的分布特性和算法的寻优范围，使得算法精度和收敛速度得到较大提高。本算法主要有以下两点改进。

1)优化初始种群位置

即使没有先验知识的情况下，利用反向点，也能获得一组较好的初始候选解(初始种群)。过程如下：

①随机初始化种群P。②计算反向种群OP，即

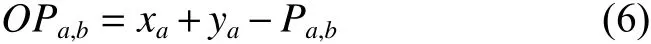
式 中 ： a =1,2,···,Np； b =1,2,···,n ； O Pa,b和 Pa,b分 别表示反向种群位置与种群位置中a维第b个变量的值；分别表示第a维元素的最大值和最小值。

③分别计算P与OP中个体的适应度，从中取适应度值较好的n个体生成新的初始种群NP。

2)优化迭代过程中的种群位置

同理，如果在迭代的过程中也使用类似的反向学习方法，就能够提高算法的全局搜索能力。算法迭代开始前，设置反向学习优化选择概率p。每当完成一次迭代，计算出新的种群位置后，依据p来决定是否对种群进行反向学习优化(p的大小根据实际需要决定)。过程如下：

①生成一个随机数rand(0,1)。如果rand(0,1)＜p，则转入②，否则，直接进入算法下一轮迭代。

②计算动态反向种群OP：

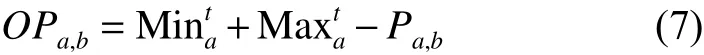
式中， M inta与 M axta分别表示第t次迭代第a维元素的最小值与最大值。

③使用适应度评价函数计算P和与其对应的OP中个体的适应度值。如果，则用OPi替代Pi，全部比较、替换后的种群P就是新的种群。其中，、分别表示第i个个体和与其对应的反向个体的适应度值，OPi表示第i个反向个体。

④进入下一轮OKH迭代。

随着搜索进程的深入，当前迭代的搜索区间远小于最初的搜索区间，使得种群快速逼近最优解。

OKH算法流程：①参数初始化，即最大迭代次数I、种群规模N、最大扰动速度Dmax、时间间隔以及优化选择概率p；②初始化种群位置并利用反向学习优化初始种群位置；③计算此时每个磷虾个体对应的适应度值；④分别计算受诱导运动、觅食行为、随机扰动所产生的个体位置变化量；⑤使用公式(5)更新磷虾位置；⑥生成rand(0,1)，如果 rand (0,1) ＜ p，根据公式 (7)计算动态反向种群并计算P与OP中个体的适应度值。如果，则用OPi替代Pi，生成新的种群，否则直接进入⑦；⑦计算磷虾个体新位置矢量的适应度，然后重复④～⑦，直到达到最大迭代次数，算法结束；⑧输出最终的迭代结果，即最优解。

1.3 算法性能分析

为了验证OKH算法，选择6个基准测试函数进行仿真分析并与标准KH算法、PSO算法作比较。测试函数见表1。

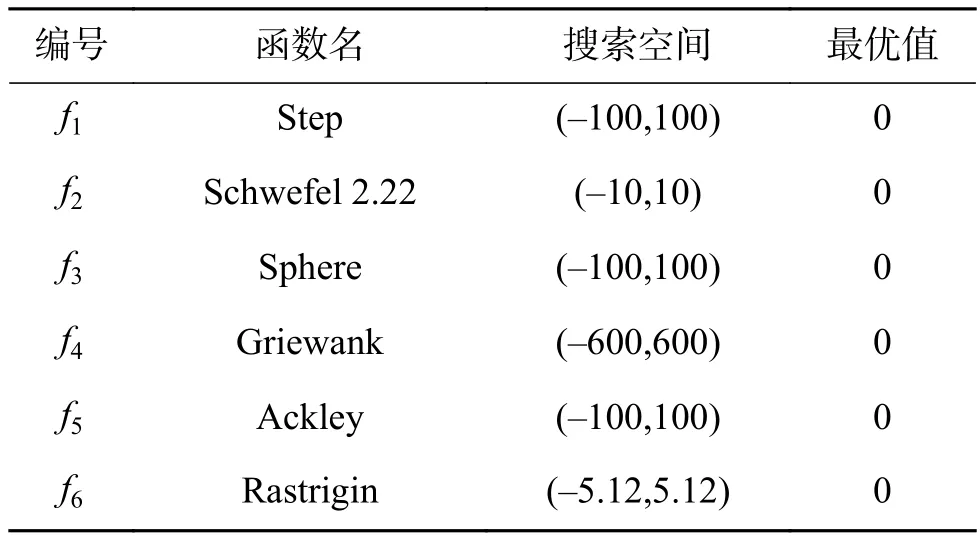
表1 测试函数Table 1 Test functions

OKH算法和KH算法的参数设置一致：最大扰动速度Dmax=0.005 m/s，觅食速度Vf=0.02 m/s，最大诱导速度Nmax=0.01 m/s。特别的，OKH中反向学习优化选择概率p=0.5。PSO参数设置为学习因子c1=c2= 1.5。为保证公平性，3种算法的其他参数一致：初始种群规模为30，最大迭代次数为200，维数为10，运行次数为10。将10次寻优的最优值、最差值、平均值以及均方差记录下来。实验结果如表2所示。

表2 3种算法的性能比较Table 2 Comparison of three algorithms

由表2可以发现，相较于KH算法、PSO算法，OKH算法具有更好的寻优效果。尤其在多峰函数中表现更为优异，不仅搜索精度更高而且跳出局部最优的能力更强。从均方差可知，OKH算法的鲁棒性也优于另外两种算法。

2 基于OKH-ELM的目标威胁估计

2.1 目标威胁估计因素

目标威胁估计问题需要统筹的因素很多，比如天气、地形、敌、我、邻军的战斗力及兵力部署和指战员作战风格等[15-16]。进行威胁估计时，通常需考虑以下的因素：

1)目标类型：大型目标(强击机、轰炸机等)、小型目标(隐身飞机、空地导弹等)、武装直升机。

2)目标速度：如 30 m/s、44 m/s、120 m/s等。

3)目标方位角：如 3°、6°、9°等。

4)目标高度：如低空、中空、高空。

5)目标抗干扰能力：如无、弱、中、强。

6)目标距离：如50 km、100 km、150 km等。

2.2 OKH-ELM目标威胁估计模型

对于随机产生初始输入权值和阈值的极限学习机,很难保证训练的ELM模型拥有较好的泛化能力和较高的预测精度[17-18]。针对以上不足，本文在采用极限学习机建立目标威胁估计模型的基础上，利用OKH算法优化ELM初始输入权重和偏置，提出了基于OKH-ELM的目标威胁估计模型。模型优化过程如图1所示。

1)数据预处理

收集105组数据，大型目标、小型目标和武装直升机各35组。随机选择大型目标、小型目标和武装直升机各30组，共90组，做训练集，剩余15组做测试集。部分数据如表3所示。

使用9级量化理论对威胁属性量化[19]。对定性属性做如下预处理。

①目标高度：超低、低、中、高，依次量化为2、4、6、8。

②目标抗干扰能力：强、中、弱、无，依次量化为 2、4、6、8。

③目标类型：大型目标、小型目标、武装直升机依次量化为 3、5、8。

对于目标距离、目标方向角和目标速度则直接进行归一化操作。

2)确定ELM网络拓扑结构

ELM隐含层神经元个数与训练集样本个数有关，经多次实验，设置20个神经元预测结果较好。ELM三层网络拓扑结构为6-20-1，输入层与隐含层间连接权值及隐含层神经元阈值的寻优范围均为[-1,1]，隐含层激活函数为Sigmoid。

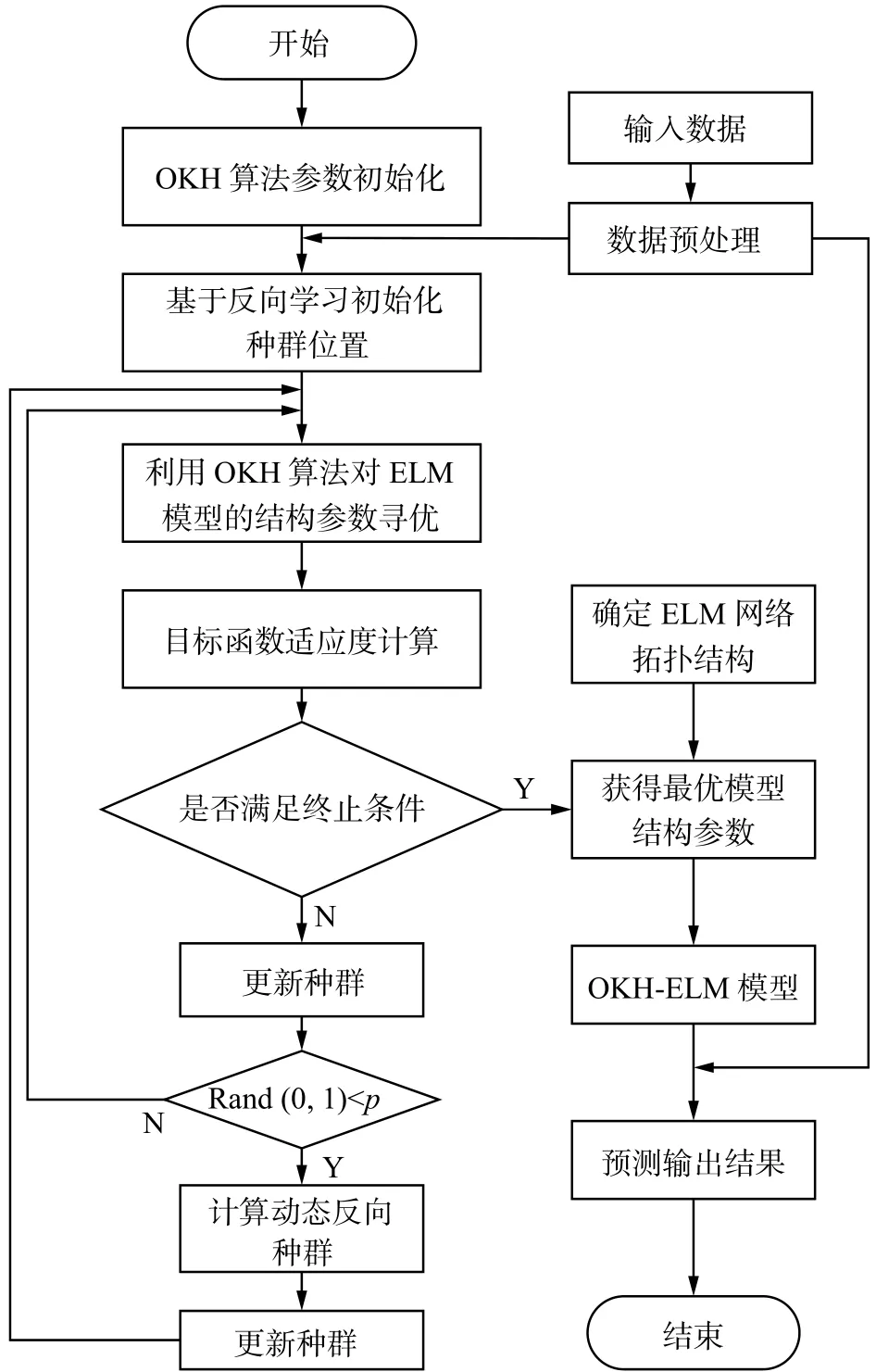
图1 基于OKH-ELM的目标威胁估计模型Fig. 1 Model of target threat assessment using OKH-ELM

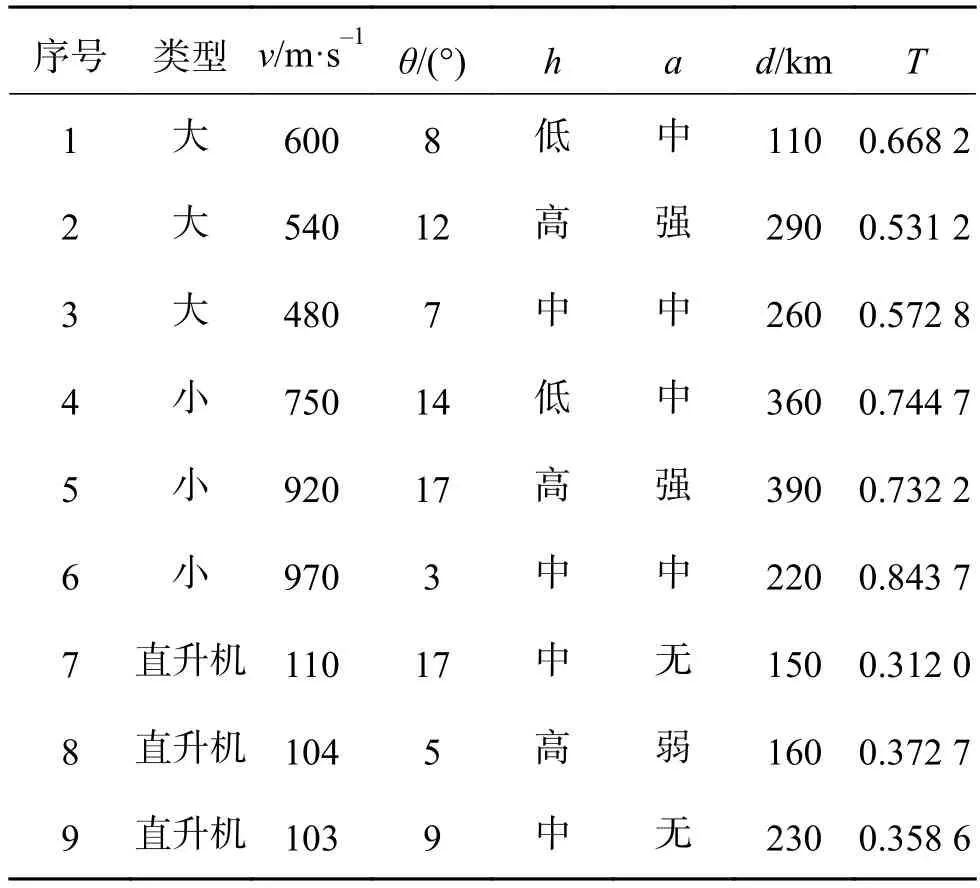
表3 部分数据Table 3 Parts of data

3)OKH参数初始化

OKH算法的参数设置与1.3节的OKH参数设置相同。

4)OKH初始化种群

个体编码方法采用实数编码，用实数串表示每个个体。该实数串由ELM输入层与隐含层之间的权值和隐含层的阈值两部分组成。因为ELM网络结构为6-20-1，所以磷虾个体的编码长度为 6×20+20=140。

5)目标适应度函数

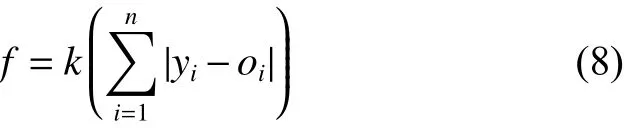
式中：n为测试样本数，yi为模型的训练输出威胁度，oi为实际威胁度，k为常数。

6)执行OKH算法

OKH算法流程与1.2节的OKH算法流程相同。

7)预测输出

利用OKH算法优化好的初始权值与阈值来构造ELM。将测试集数据输入已经训练过的ELM，预测目标威胁度。

3 模型性能分析

为测试OKH-ELM目标威胁估计模型的有效性，将测试数据分别输入OKH-ELM、ELM、KHELM、KH-BP、PSO-ELM模型比较预测输出。

KH-ELM模型、PSO-ELM模型的建立与OKH-ELM相似，仅将优化函数分别改成标准KH算法和PSO算法。KH-BP模型利用KH算法优化BP神经网络初始的全部权值和阈值[20]，采用6-11-1的网络结构，磷虾个体编码长度为6×11+11+11+1=89。采用训练好的上述5种模型分别对相同的威胁度测试集进行预测，实验结果如图2、图3和表4所示。

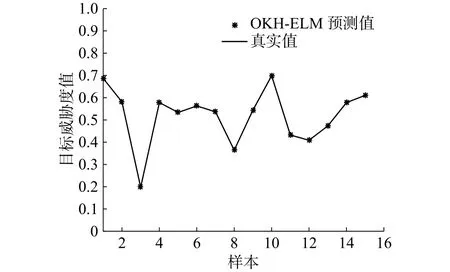
图2 OKH-ELM的预测威胁值与真实威胁值对比Fig. 2 Comparison between forecasting values and real threat values based on OKH-ELM

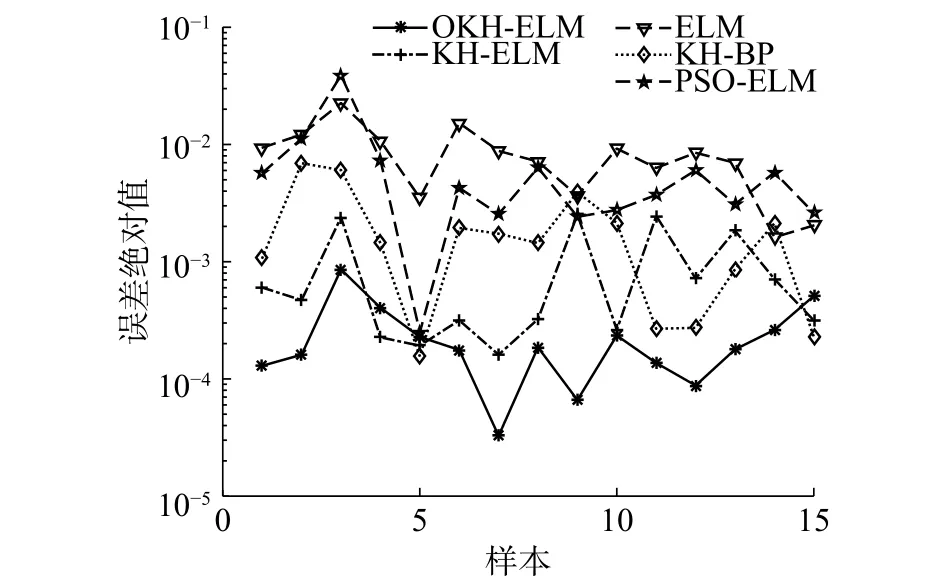
图3 5种模型的预测误差绝对值Fig. 3 Absolute predictive error for five models

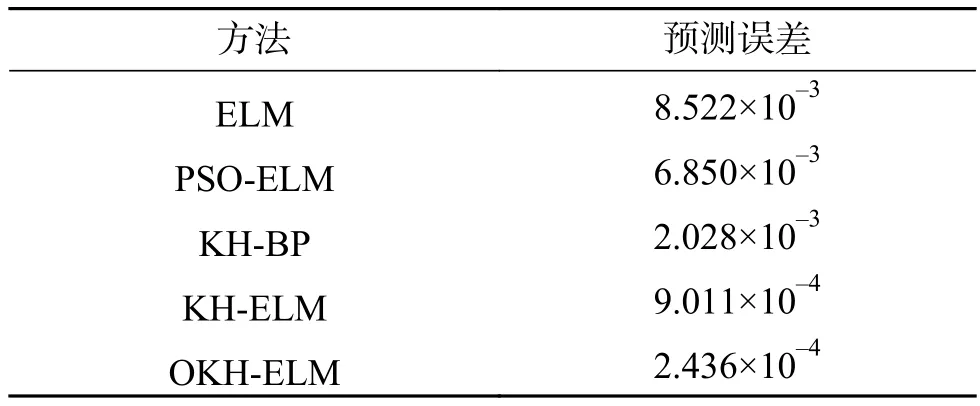
表4 5种优化方法的绝对预测误差平均值Table 4 Average of absolute predictive errors of five optimization methods

由图2可知，OKH-ELM模型输出的预测威胁值与真实威胁值拟合度很高。由图3、表4可知，OKH-ELM威胁估计模型的预测误差平均值小于其他4种威胁估计模型，预测结果最接近真实值。除了在第4、5、15个样本处，OKH-ELM模型预测误差不是最小(但也十分接近最小误差)，其余样本点预测误差均最小。5种模型的优异度排序为：OKH-ELM＞KH-ELM＞KH-BP＞PSOELM＞ELM。实验结果显示，本文构造的OKHELM目标威胁估计模型能够较好地应对目标威胁估计问题，模型性能优于另外4种模型。

4 结束语

本文针对多源信息融合中目标威胁估计的特点，利用改进磷虾群算法与极限学习机，建立了一种基于改进磷虾群算法优化极限学习机的目标威胁估计模型，并提出了该模型的算法。文中选取影响目标威胁估计的6个典型指标，采集了105组数据用于仿真实验。结果表明，相比于ELM、PSO-ELM、KH-BP、KH-ELM，OKH-ELM模型能够更加准确、有效地预测目标威胁值，为目标威胁估计提供了一种新的方法。