如何在数学探究活动中充分利用各类教学资源——以“乘加、乘减解决问题”教学为例

江苏省常州市武进区实验小学 吴志远

“乘加、乘减两步计算解决问题”是二年级下册中的内容，之前学生学习了加减法两步计算解决问题，主要是求和，还有比较多少问题，只要涉及差值计算，而“乘加和乘减分步计算”则主要针对倍率关系计算。因此，学习本知识之前，学生已经积累了分步计算的经验，搭建了分步计算的模型，在此基础上进一步强调计算顺序。紧紧依靠教材，相机处理教材，才能起到实效。

一、活用“学生”资源，调动儿童思维活动

教育家陶行知先生曾言道：“教学内容和教学方式，绝不是凭空臆造，都是遵循人的发展需求，人的需求不同，则内容和方法均不同，教育方式、处置轻重、教学次序都会随之变化。”这句话至今仍不过时，教师要善于分析学情，充分开发利用“学生”资源，为课堂教学服务。

例如，针对小班教学。小班就是“以学定教，提高课堂效率”的最好施展舞台。研判学生的知识基础和接受能力，笔者采纳了异形组合为主、同质组合为辅的方式，来进行排座分组。

新课程的核心理念是，兴趣为先导，知识为负载，过程为评议标准，信心的重要性比成绩的重要性要大。于是，笔者综合考虑学生的现状与差异，科学合理分配小组，二次挖掘学生资源，辩证统筹同形组合和异形组合规则，这样最大面积、最大限度激发了群体热情，鞭策他们以充沛的感情，积极的态度，活跃的思维，迎接新知识的洗礼。

二、细化“目标”资源，引导儿童获取新知

教师对知识的“最近发展区”应该深入调研，学习的本质是在接受能力许可的直径内，囊括吸纳新的认知，满足自我实现的需要。因此，教师必须摒除成人的保守思维，抛弃成人已知先知的带来的重建障碍，在学生的已知和未知之间，开凿一条高速通道，让学生经过摸索探究后沿着预定轨道抵达终点，指点的痕迹不能太明显，要多暗示少明示，要让学生自己体验到成功的喜悦。因此，根据学生的不同情况，制订了如下教学目标。

基本性目标：

1.在具体教学情境中，使学生透彻理解数学问题的含义，学会运用乘加、乘减两步计算间接求解法。

2.初步分辨分步算式、综合算式的联系和区别，感知两步求解的过程。

发展性目标：

1.分组探究，培养学生独力思考解题能力。

2.初步培养学生多元化思考、多策略应对的思维模式，如通过线段图、列表等建立展示分析数量关系。

另外，按照“以生为本，构建童心的课堂”的理念要求，对于这节课，分层设定目标。高级目标：学习能力处于A、B等级的学生，能熟练列出分步算式和综合算式。

基础目标：学习能力处于C档的同学，能在合作环境下提出问题并顺利解决；学习能力处于D档的同学，在老师的提点下，能够用分步算式解决乘加、乘减问题。

三、巧设“环节”资源，建构儿童有效课堂

步骤一：创设情境，出示情境图（略）。

提出问题：欢乐谷里参观的有几人？坐过山车的有几人？欢乐谷里一共有几人？直接从学生的知识基础和学习能力出发，试探他们的读图、提取数字信息、提出问题的能力。

步骤二：独力探究，合作交流。

1.独力探索。

提出问题：坐过山车的一共有多少游客？怎么计算？请将自己的思路，与同学交流一下。想出的方法越多越好。

2.小组讨论。

分析前测形势，大部分学生感觉很容易，主要难点集中在分步算式向综合算式的转化，对运算顺序的理解有障碍。因此，通过小组合作的助推，让先学会的学生教导后学会的学生，让不同资质的学生带着不同的任务展开交流，教知识，教方法，最大限度利用学生资源。

3.集体交流。

根据学生的反馈，整理不同的解题方法。

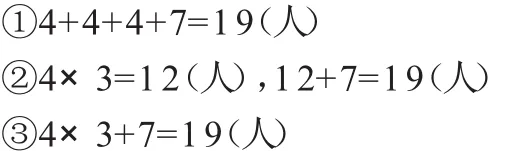
个性解决：7+4×3=19（人）反馈时，抓住以下两点进行交流。

(1)理清不同方法的关联度。

乘加互换：算式4+4+4+7简写成4×3+7。

分步整合为综合：先算坐过山车游客人数，再计算欢乐谷总游客数，整体思路是一致的。

(2)综合算式数字顺序与计算顺序辨析。7+4×3，行吗？小组讨论并思索，7+4×3与4×3+7，这两个算式虽然数字顺序不同，但是，计算顺序却相同，都是先算4×3，算出坐过山车人数，再算欢乐谷里的总游客数。在探究过程中，重点探讨算式形式与算理，实现解题算式多样化。

环节三：学以致用，深入开发练习效果，设计变式习题、拓展训练，不但要巩固，还要拓展延伸，既符合学生的“思维最近发展区”，也容易刺激学生未来深造区。

加强对比练习，理清运算顺序。

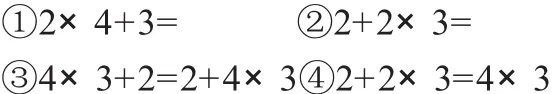
研究错例：2+2×3=4×3，对吗？错在哪里？如何修改？让乘加中引入小括号概念。

数学课堂具有开放性，是不断发展变化的过程，而学生掌握知识技能，也需要一个反复试错磨练的过程，并非一蹴而就。因此，面对“错例”，不要慌乱，也不要排斥，更不能回避和全盘否定，应及时加以疏导和改造，在错误中找出有价值的地方，让学生审视问题的角度更宽广，思维更成熟。在纠错过程中深化对知识的理解。

总而言之，在数学教学中，教师要充分盘活各种资源，结合低龄儿童的心理特征和认知规律，采取符合儿童心智特征的教学方式，达到“以学定教”的目的。这样，才能真正做到让学生善学乐学！让数学课堂充满生气！