谈课程资源的整合—— 以“直线与平面垂直”的教学为例

☉江苏省口岸中学 杨 翠

随着时代的发展，越来越多的技术和理论融入了我们的教学，这些都是需要我们妥善使用的课程资源.笔者认为，我们的教学不但要让这些新兴资源物尽其用，更要让一些传统资源也能发挥其作用.下面笔者就以“直线与平面垂直”第一课时的教学为例，探讨一下自己对这一问题的看法.

一、新课导入

师：物体形状、大小以及位置等方面的特征是几何研究的主要内容，而平行和垂直是最为特殊的两种位置关系，在之前的学习过程中，我们已经认识过平行，今天我们所要研究的问题是垂直.

（教师板书：直线与平面垂直的判定）

设计思路：由于课前学生已经拿到学案进行了预学，再加上教材上的描述也比较完备，所以学生已经知晓即将研究的内容和目标.因此，教师直奔主题，通过语言引导并辅以板书，强化学生的目标意识，揭示了课题.

二、活动开展

探究活动（一） 探索线面垂直的概念

1.引导学生在阅读中提炼知识

师：请大家结合学案上的安排，阅读教材上有关线面垂直的内容，请将你认为重要的文字圈画出来.

（学生按照要求开始阅读）

设计思路：在整合教学资源的过程中，教师要引导学生充分用好教材，而最佳的使用方式就是阅读，所以课堂绝不是导学案的独角戏，更不是课件的展示平台.此外，学生的阅读能力和概括能力在阅读过程中都能得到发展.

2.通过问题来引导学生探索

师：请你围绕线面垂直，列举一些生活中实例.

生：马路边路灯杆子和地面的垂直关系，教室里墙壁的边线和地面的垂直关系等等.

（教师再通过一些图片来进行适当补充，丰富学生的感性认识）

设计思路：生活应该是学生建构认识最为基础的源泉，教学中让学生列举生活实例可以唤醒学生的回忆，由此让学生围绕已有认知来建构认识，同时他们数学直观的相关素养也会得到发展.

师：如图1所示，AB表示的是一根旗杆，BC是太阳光照射下它的影子，请问它们之间有着怎样的关系？随着时间的推移，BC位置会发生调整，它们的关系又如何？AB与其他不经过B点的直线又有怎样的关系？

生：它们都有相互垂直的关系.

（教师同步以课件的方式进行了动态演示）

设计思路：这里的教学，我们充分利用多媒体课件的优势，让原本静态的数学知识以动态的形式展示出来，有效激活学生思维，有助于学生加深理解和认识.

师：你能总结出线面垂直的概念吗？

（学生在问题的引导下，展开讨论，他们在相互讨论中强化了理解和认识）

结合学生的展示，教师板书如下：

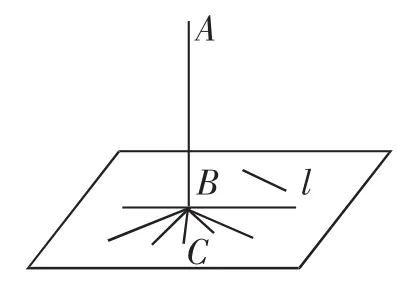
图1

设计思路：概念教学是本课的一大重点，教师要充分尊重学生的主体意识，引导学生在探索中进行总结.而且，教师还要适当地进行板书，将文字语言翻译为数学语言，以此来加深学生的印象.

3.引导学生在辨析中理解

师：以下有关线面垂直的表述正确吗？请阐明理由.

（1）若存在某直线和一平面中的无数条直线垂直，则直线垂直于该平面；

（2）若一直线垂直于某平面，则该直线和平面中的任意一条直线垂直；

（3）如果直线与平面中某一条直线不垂直，那么该直线必然与平面之间没有垂直关系.

（学生先进行思考，并在小组讨论中完善自己的答案）

设计思路：上述问题都是对线面垂直概念的直接辨析，三个问题可以让学生从不同角度来形成对线面垂直的认识和理解.

探究活动（二） 探索线面垂直的判定定理

1.指导学生在操作中展开探索

师：请大家拿出课前准备的三角形纸板，我们一起来完成一个实验，过△ABC的顶点A对纸片进行翻折，由此可以得到一个折痕AD，将翻折后的纸片放在桌面上，使得BD、DC接触桌面，请大家进行观察和思考：折痕和桌面垂直吗？

（学生自主展开实验，由于折痕的操作具有随意性，有的小组汇报折痕与平面垂直，有的小组汇报折痕与平面不垂直.这时教师引导学生展开比较，他们发现构成垂直关系的三角形折痕如图2所示，判定定理呼之欲出）

图2

设计思路：这一实验操作将学生充分发动起来，他们在主动操作中展开比较和思考，进而明确了继续探索的方向.

教师发动学生重复之前构成线面垂直关系的那一组学生的操作，并启发他们对结论进行总结.当学生汇报了自己的结论之后，教师再安排学生回归课本，结合教材上内容的表述进一步明确认识.

设计思路：这一块是本节内容的重点所在，教师在授课时要充分整合实验、课件等资源，让学生在自主操作中形成认识，这样的处理能够有效引导学生发现问题，并解决问题，学生通过自己的双手来发现结论，能够产生更加深刻的印象.

2.通过问题来引导学生深入探索

师：请复述你对判定定理的认识，你能用符号进行表达吗？

设计思路：针对重要的概念和理论，教师让学生进行复述可以起到强调的效果，而且安排学生用数学符号进行表述，有助于提升他们对符号语言的熟悉程度.

3.通过典型例题来帮助学生巩固认识

师：大家看到学案上所准备的两个问题，请尝试解决.

例1 如果a∥b，a⊥c，那么b⊥c吗？请说明原因？

例2 如图3所示，如果a∥b，a⊥α，那么b⊥α吗？请说明原因.

图3

学生完成对两个问题的作答后，教师则继续引导学生围绕两个问题进行总结：（1）如果两条平行直线中的某一条垂直于已知直线，那么另一条也垂直于已知直线；（2）如果两条平行直线中的某一条垂直于已知平面，那么另一条也垂直于已知平面.

设计思路：学习立体几何有着这样的重要方法，即类比平面几何的知识来学习立体几何的知识，将立体几何问题转化为平面几何问题来处理.在这里，我们通过例1来唤醒学生的回忆，再通过例2来引导学生采用类比的方式总结出判定线面垂直的又一个方法.这样的过程降低了知识的获取难度，学生更容易理解，同时立体几何和平面几何相互转化的思路也将深入他们的大脑，进而形成一种自觉的意识.

三、随堂检测

师：请大家完成以下问题.

习题：如图4所示，在三棱锥VABC中，已知VA=VC，AB=BC，且K为AC的中点.

（1）求证：AC⊥平面VKB；

（2）求证：VB⊥AC；

（3）如果AB的中点为E，BC的中点为F，请分析EF和平面VKB之间的位置关系.

（学生自主探究，教师安排部分学生进行板演处理）

设计思路：学生在探究过程中已经对基本规律形成认识，这时教师要结合习题来对学生的掌握情况进行检查，这一过程事实上也将促使学生进一步熟悉规律的使用.

图4

四、课堂小结

最后在课堂小结阶段，教师安排学生自主进行总结，有助于学生巩固自身认识，教师结合板书和课件将知识脉络呈现出来，能够让学生更加清晰地把握知识结构.

综上所述，在高中数学教学的过程中，教师要善于使用各类教育资源，同时我们还必须深刻认识到：学生不仅是我们的教育对象，更是一种资源，发动学生积极参与科学探究，有助于提升他们的认识效率.