铁路环形班列开行方案优化方法研究

马 利，王鹏翔，李海鹰，王 莹

（1.中国铁路北京局集团有限公司 货运处，北京 100860；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；3.北京交通大学 交通运输学院，北京 100044)

随着国家经济结构转型升级，铁路部门于2014年开行了环形班列，专门受理区域零散货物快运业务。环形班列为区域经济的发展起到了良好的促进作用，但在运营过程中仍存在一些问题，一是班列在运量小的车站停站过多，影响了环形班列的运输时效；二是班列开行时间与货流需求配合难度大，导致货物在车站的等待装车时间过长。这些问题降低了班列运输的时效性，一定程度上影响了环形班列对货主的吸引力，因而有必要对环形班列开行方案进行优化，提升市场竞争力。

环形班列提出的时间较晚，专门针对其开行方案的研究基本处于空白阶段，普通快运班列开行方案的研究主要集中在班列开行频率和运输路径的选择上，涉及到班列开行具体时间的研究较少。Jeong[1]以最小成本为目标函数建立模型，考虑了运输成本问题，对开行进路的选择、开行数量的确定等问题进行了研究。张文斌[2]利用复杂网络的方法对行包运输网络进行了研究和规划。李昂[3]考虑站点之间的距离，以“门到门”广义费用最小为目标对环形班列停站方案进行了优化，解决了班列停站过密的问题。赵婷[4]考虑了货源情况、路网能力、编组辆数、经济条件等影响因素下的开行方案编制问题，对班列的开行频率和停站方案进行了优化。王莹等[5]对路网条件下多方式、多模式的“五定”班列开行方案的优化方法进行了研究。李海鹰等[6]以动态服务网络为基础，引入了货物发送、到达和运输时限3个时间窗对班列运到时限进行约束，以利润最大为目标建立了班列开行方案优化模型，并设计了相应的启发式算法进行求解。杨毅凡[7]综合考虑了运送的需求量最大化、铁路运营效益最大化、货主成本最小化3个目标下开行方案的编制问题。张玉召等[8]以货运量最大化及货主支出运输成本最小化为目标，构建快捷货物列车开行方案的多目标优化模型，实现了货流在可选走行路径上列车内的分配。李小波[9]按不同班列产品分析影响快运班列运输时效性的主要因素，提出了提高铁路快运班列运输时效性的方法。综上，在现有研究的基础上，以动态服务网络为基础，重点考虑班列的时效性，对环形班列开行方案优化方法进行研究。

1 铁路环形班列动态服务网络构建

每趟环形班列都可以为其所经过的站点提供运输服务，如果将这些运输服务看作站点之间的弧，那么班列开行方案编制问题就可以转化为动态服务网络设计问题。

用G= (N，A)来表示动态服务网络，其中N为网络中的节点集合，表示带有时间属性的站点；A为网络中弧段的集合，是环形班列提供的运输服务集合，包括运行弧As和停站弧Aw。运行弧表示班列在线路上运行，其弧长表示两节点之间的运行时间；停站弧表示班列在车站停站，其弧长表示班列在该站的停留时间。

动态服务网络构建方法如图1所示，环形班列基础路网如图1a所示，在其基础上简单建立的环形班列动态服务网络如图1b所示。在图1b中，同一列的点代表同一站点的不同时间状态，同一行的点代表同一时间状态下的不同站点，黑色实线代表运行弧，黑色虚线代表停站弧。A与A'都表示中心站，A表示始发状态下的A站，A'表示终到状态下的A站。网络中的弧首尾相连构成一个班列运输路径，图中的路径表示t1时刻由A站出发，最终在t16时刻返回A站的班列，运行途中在中间站点B，C，E分别停留了一段时间进行装卸作业，停站的时刻依次为t5，t9和t13。

通过这种方式可以将班列的开行方案用上述动态服务网络来表示，对于一个特定的服务网络，可以通过配流，得到各个需求的运输路径，从而计算货物运输过程中的各项费用指标，而不同的网络结构代表不同的开行方案，其配流结果不同，各项费用指标也不同。开行方案优化问题，对应在服务网络上则是在给定运输物理起点、终点条件下，利用网络设计优化的理论，获得使费用和收入等指标最优的班列运输路径，从而得到一个快捷、经济、高效的班列开行方案。

2 铁路环形班列服务网络优化模型

环形班列服务网络设计就是确定各班列在网络上的运输路径，通过减少货物等待装车时间及旅行时间来提高班列运输的时效性，因而在模型中引入出发时间窗和到达时间窗对等待装车时间和旅行时间进行约束，对超出约束的部分进行惩罚，从而达到提高班列时效性的目的。据此，以总利润最大为目标，以网络容量为约束，以服务弧是否被构建及各站之间的运输需求是否被满足为决策变量构建环形班列服务网络优化模型。

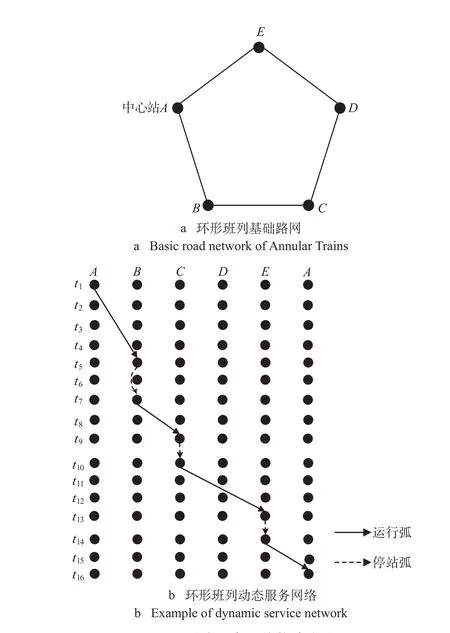
图1 动态服务网络构建方法Fig.1 Establishment of dynamic service network

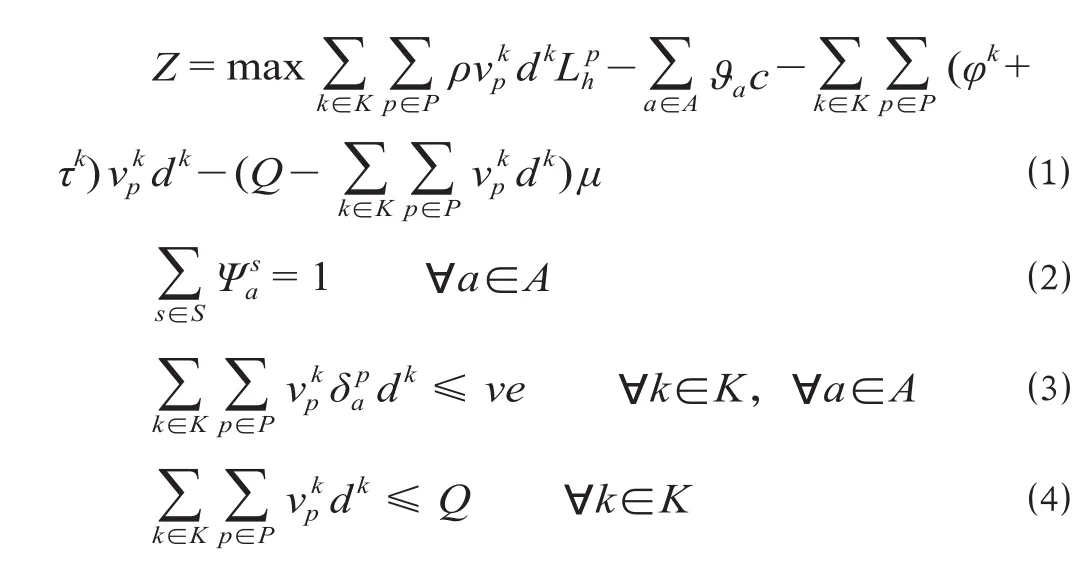
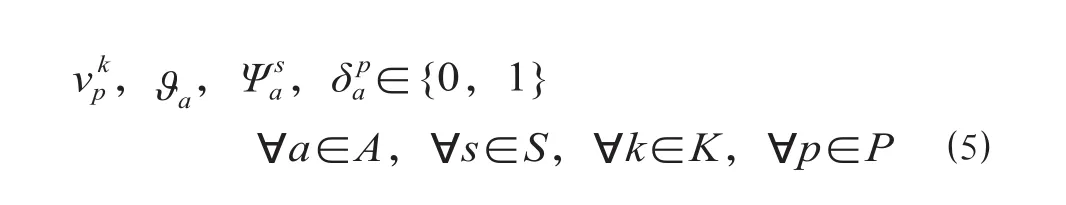
式中：v为列车最大编挂辆数；e为车辆标准载重；S为班列集合；A为服务网络中弧的集合；K为OD需求集合；dk表示需求k的需求量大小；P为需求经过的路径集合；ρ为运输收入；c为班列固定成本；μ为需求不满足时的惩罚费用；Q为周期内OD需求总量；φk和τ k分别为出发时间窗惩罚函数和到达时窗罚函数；为0-1变量，当取值为1时表示服务弧a属于班列s；ϑa为0-1变量，当取值为1时表示弧a是始发弧；为0-1变量，当取值为1时表示需求k被路径p运送；la为弧a对应的物理区段的里程；为0-1变量，当取值为1时表示弧a属于路径表示路径p的里程，其中，模型的决策变量为前者决定了班列的发车时间和停站方案，后者决定了在特定网络结构下各弧段的流量分配情况。

⑴ 式表示模型目标为利润最大化，该利润由运输收入、班列固定成本、时间窗惩罚费用和未完成周期内全部需求的惩罚费用4部分组成。在目标函数中引入货物的发送和到达时限惩罚项对等待装车时间和旅行时间进行约束，尽可能地满足货主对于运到时限的要求。其中，φk和τ k分别为出发时间惩罚和到达时间惩罚，具体取值如下。①出发时间惩罚。出发时间惩罚是指货物必须要在规定的时间段内发出，否则就给予一定的惩罚。出发时间惩罚能够有效地对货物在车站等待装车时间进行约束，计算公式为其中，tps为需求k的实际发车时间；为需求k的期望发车时间，不同种类的需求具有不同的期望发车时间；ω为出发惩罚系数。②到达时间惩罚。到达时间惩罚是指货物必须要在规定的时间内到达，否则就要给予一定的惩罚，在出发时间惩罚的基础上对到达时间进行惩罚，能够有效地对旅行时间进行约束，从而减少班列不必要的停站，计算公式其中，tpe为需求k的实际到达时间；Tak为需求k的期望到达时间，不同种类的需求具有不同的期望到达时间；σ为到达惩罚系数。⑵ 式是服务弧的逻辑约束，表示网络上的服务弧必须属于班列运输路径的一部分。⑶ 式为班列容量约束，表示班列上装载的运量不超过班列的运输能力。⑷—⑸ 式是逻辑约束。⑷ 式表示总运量不能超过总运输需求。⑸ 式表示变量取值为 0或1。

3 算法与实例分析

3.1 求解算法

上述模型是一个大规模混合非线性整数规划模型，传统的数学优化方法求解较为困难，根据问题的特性，将开行方案优化拆分为“停站方案优化”和“发车时间优化”2个阶段顺次计算，分别设计遗传算法和启发式算法进行求解，进而得出最优的班列开行方案，算法流程如图2所示。

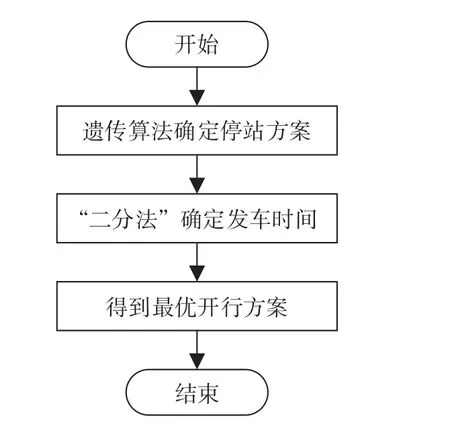
图2 算法流程图Fig.2 Flow chart of algorithm

3.1.1 确定停站方案

由于停站方案的决策变量为0-1变量，采用遗传算法编码方便，适合求解。结合问题特征，采用0-1变量对染色体进行编码，1代表在该站停站，0代表在该站不停站，基因编码如图3所示，适应度函数采用模型中建立的目标函数，交叉方式采用单点交叉，种群规模设为32，交叉概率设为0.3，变异概率设为0.1，当种群适应度函数趋于稳定时终止算法。遗传算法流程如下。

步骤1：生成初始染色体种群，包含16条染色体。

步骤2：按次序计算每一条染色体的适应度函数。

步骤3：判断是否达到终止条件，是则转到步骤6，否则继续向下执行。步骤4：通过轮盘赌算法对染色体进行选择。步骤5：对染色体进行交叉、变异以产生新一代种群，转到步骤2。

步骤6：算法终止，种群中适应度函数最大的染色体对应的停站方案即是最优停站方案。

3.1.2 班列发车时间优化

考虑到班列可选的发车时间较多，研究采用逐步逼近的思想，设计了基于“二分法”的启发式方法，通过反复迭代逐步逼近最优解。首先，将周期内每一天划分为2个等分时间段，规定周期内每趟班列的发车时间只能是时间段的下限，即12 : 00或24 : 00，通过枚举法计算出周期内班列发车时间的最优组合；在此基础上，将每趟班列发车时间所在的时间段继续细分为2个等分时间段，通过枚举法找出此精度下最优的发车时间组合，循环往复，直到满足精度要求为止。“二分法”流程如下。

步骤1：初始状态，时间段长度为1 d，没有进行拆分，每趟班列发车时间默认为24 : 00。

步骤2：将时间段拆分为更小的2个时间段，拆分后的2个时间段的长度必须为服务网络时间段长度的整数倍，拆分时保证拆分后的时间段长度相同或相近。

步骤3：通过枚举法计算出本精度条件下最优发车时间组合。

步骤4：判断是否达到精度要求，是则转到步骤6，否则继续下一步。

图3 基因编码Fig.3 Gene encoding

步骤5：选取步骤3得到的每趟班列发车时间，将其所在的时间段作为下轮循环拆分的时间段，转到步骤2。

步骤6：算法终止，所得到的发车时间组合即为要求精度下的最优发车时间组合。

3.2 实例分析

采用京津冀环形班列北逆环线的数据进行实例验证，北逆环线共41个站点，里程1 379 km，原有方案固定每日22 : 55发车，开行频率为每日1列，在41个站点均进行停站作业。根据现有环形班列各站的运量数据，经初步测算，设计一个以3 d为周期的班列开行方式，即每天仍然开行1列，但前2天的班列仅停靠部分车站，第3天的班列在41个站点均停站。在该环形班列开行方式下，每3天为一个循环，开行2列择站停和1列站站停列车。基于该开行方式，运用优化方法，对其具体的停站方案和每日发车时间进行优化。考虑到第3天开行的班列最晚第5天才能返回，因而求解5天内班列在各站的到发时刻，如图4所示，实线为前3天发出的列车，属于周期内班列，需为其确定在各站的到发时刻，虚线为后2天发出的列车，属于下一周期，计算时不予考虑。

不同种类的需求对运输时效性有不同的要求，按时效性高低将其分为3类，并将其出发时间窗分别设为起票后的2 h，4 h和6 h；需求的到达时间窗统一设为货物最快到站后的6 h，最快到站指货物通过直达的运输方式到达目的站点。模型中的相关参数取值如表1所示。

原方案停站数量41个，采用遗传算法对停站方案进行优化，第1天停站数量减少了18个，第2天停站数量减少了17个，停站方案优化结果如表2所示。从计算结果可以看出，与优化前相比，运输利润提高了4.3%，出发时间惩罚减少了4.5%，到达时间惩罚减少了2.7%，说明优化停站后运输时效性得到了一定程度的提升，同时运输收益有所增加。

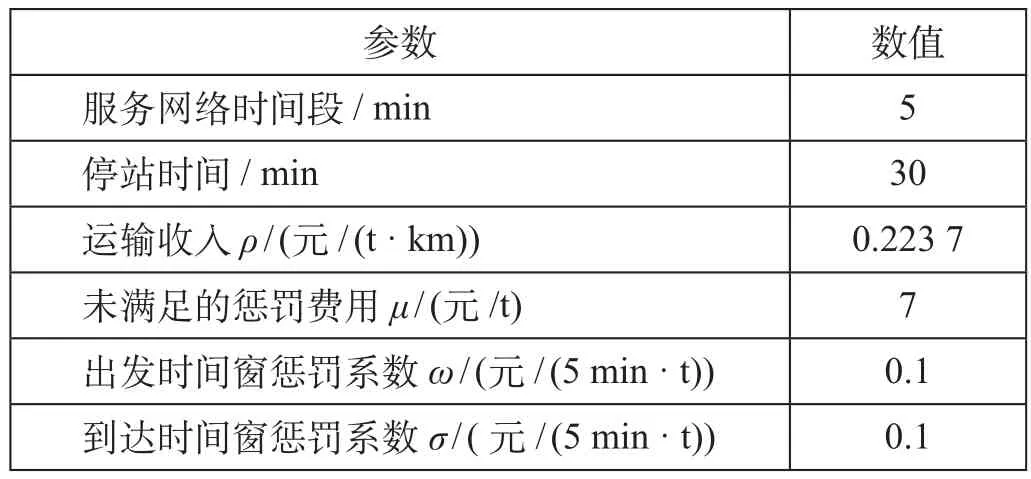
表1 参数取值Tab.1 Parameter value

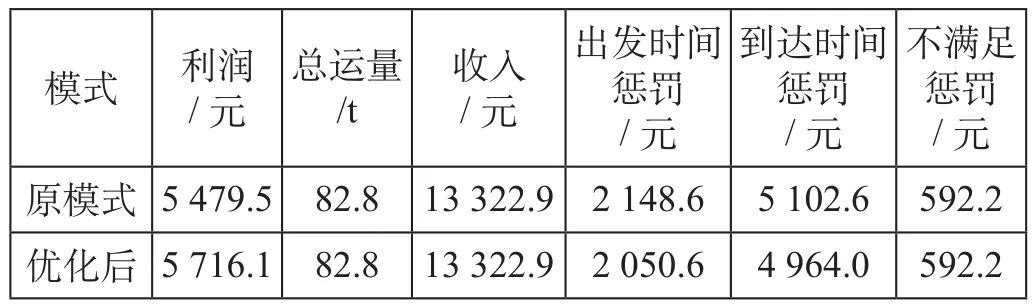
表2 停站方案优化结果Tab.2 Optimization results of stop plan

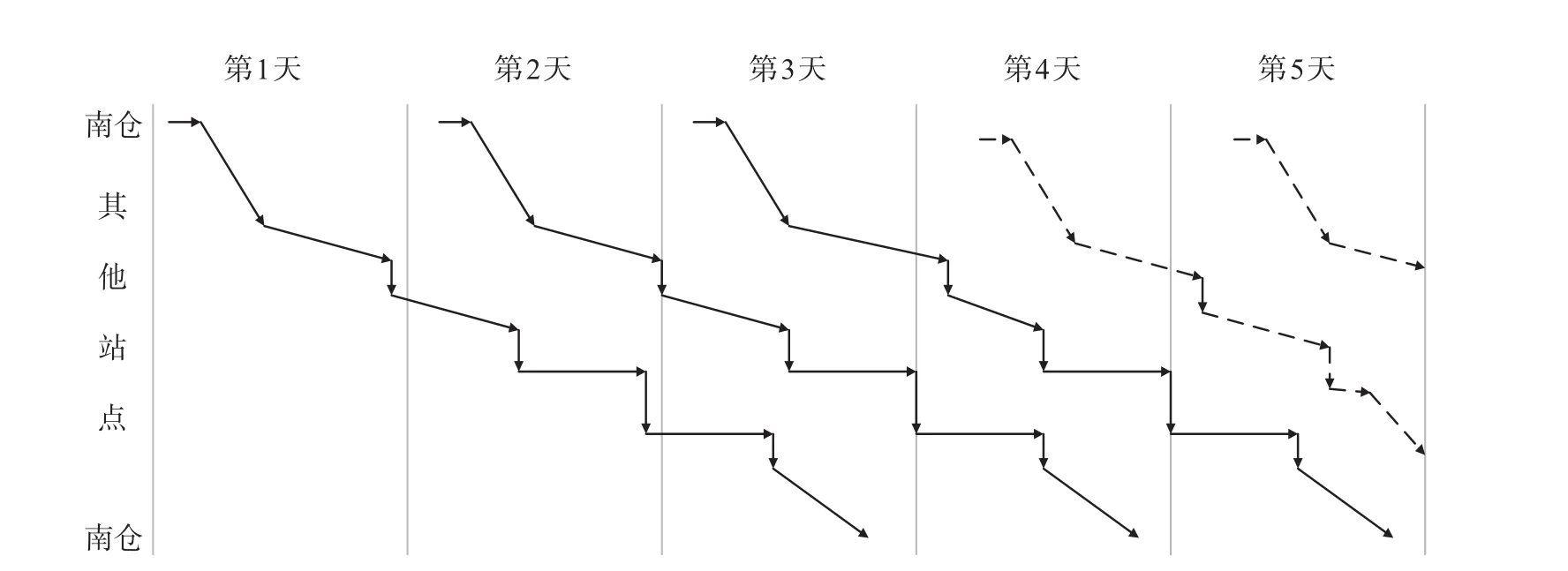
图4 运行周期示意图Fig.4 Schematic of operation cycle

在优化停站方案的基础上，进一步采用“二分法”对发车时间进行优化，班列发车时间从原先的每日22 : 55变为前2天17 : 35，第3天14 : 25，发车时间优化结果如表3所示。与优化前相比，运输利润值提高了22.4%，出发时间惩罚减少了38.8%，到达时间惩罚减少了13.3%，说明货物在车站等待装车的时间减少了很多，班列到达各站的时间更好地满足了客户需求，运输时效性得到了大幅提升，同时运输收益也有了较大提升。

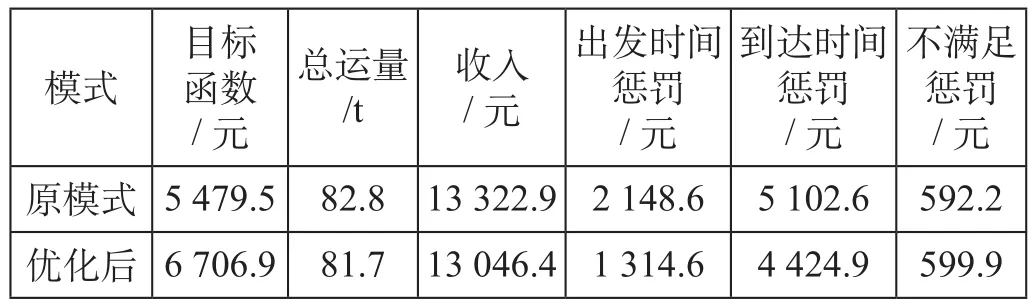
表3 发车时间优化结果Tab.3 Optimization results of departure time

由以上2步的优化结果可以看出，通过对现有班列的停站方案进行优化，运输时效性和运输收益均有所改善，但优化幅度不高。在此基础上，通过进一步优化班列的发车时间，可以大幅提升运输时效性及增加运输收益。该优化结果说明，通过合理设置班列停站方案和班列开行时间可以大幅提升环形班列的时效性。

4 结束语

铁路环形班列满足了中小企业灵活分散的运输需求，具有快捷、安全、方便的特点，适合运送小件零散货物。但是，铁路部门在提供物流服务过程中，依然存在重运输成本、轻时间成本的问题，研究以动态服务网络为基础，构建了考虑发车时间的环形班列开行方案优化模型，将问题分为2个阶段顺次求解，先设计遗传算法对停站方案进行优化，再采用“二分法”对班列发车时间进行优化，进而完成开行方案的优化。实例计算表明，该优化方法可以为环形班列发车时间、停站方案的确定提供理论指导，减少班列不必要的停站和货物等待装车的时间，从而提高环形班列的运输时效性，提升铁路运输企业的竞争力。此外，上述模型及算法经过改进，也可用于解决其他运输模式下快运班列的开行方案编制问题。