高速铁路列车运行图与动车组运用一体化优化模型与算法研究

王 超，王淑姗，王 鹏，王小京，陈 磊

（1.中国铁路总公司 运输统筹监督局，北京 100844；2.北京交通大学 交通运输学院，北京100044；3.中国铁路呼和浩特局集团有限公司 概预算审查所，内蒙古 呼和浩特 010057；4.中国铁路呼和浩特局集团有限公司 调度所，内蒙古 呼和浩特 010057)

高速铁路列车运行图和动车组交路计划是高速铁路运输组织的重要组成，是铁路组织列车开行的基础。高速铁路列车运行图规定了列车开行计划，动车组运用规定了动车组交路计划，因而应统筹考虑列车开行计划和动车组交路计划，以最少的动车组运用，达到列车开行数量的最大化，实现列车运行图和动车组运用的一体化优化。从目前研究情况看，列车运行图与动车组交路计划都是分别优化，即：列车运行图的优化，一般不考虑动车组交路计划的编制；而动车组交路计划的优化，一般将运行图作为已知输入条件，很少有研究将两者同步考虑、同步优化[1-2]。在动车组不固定运用的条件下，一旦遇到突发情况，高速铁路列车运行图结构将发生较大变化，可能会导致该运行图对应的最优动车组运用计划随之改变，最终会影响动车组的使用数量和运用效率。如果能够科学运用优化方法，及时调整动车组交路计划，可以节省动车组运用，有效提升运输效率效益。通过对列车运行图优化与动车组运用优化进行一体化考虑，研究在列车开行对数一定的条件下，如何实现车底运用数量最小这一目标[3]。

1 高速铁路列车运行图与动车组运用一体化优化模型

1.1 理论基础

车辆路线问题(VRP问题)最早是由Dantzig和Ramser于1959年首次提出，它是指一定数量的客户，各自有不同数量的货物需求，配送中心向客户提供货物，由一个车队负责分送货物，组织适当的行车路线，目标是使得客户的需求得到满足，并能在一定的约束下，达到例如路程最短、成本最小、耗费时间最少等目标。随后VRP问题由货物运输扩展到旅客运输，最典型的案例是单位巴士接送本单位员工上下班，员工居住于不同地点，需要对巴士进行径路规划。实际上，动车组在铁路网的运行过程中，将旅客从O运输到D，完全可以转化为VRP问题。列车运行图的本质是动车组运行后留下的轨迹[4]。因此，构建高速铁路列车运行图与动车组运用一体化优化模型研究是典型的VRP问题[5]。

1.2 符号说明

首先，将列车运行图与动车组运用一体化优化模型中需要使用的变量定义如下。

（1）运行图指标：A为高速铁路线路上所有车站的集合；i，j，k为该线路上的任一车站，即有i，j，k∈A；t，t'为时间索引；Bj为列车在车站j的总停站次数，次/d；B为列车在该线路上的总停站次数，次/d；C为高速铁路线路上终点站的集合；D为列车在中间站的停站时间标准，min；E为列车在终点站折返的时间标准，min；I发为该线路上列车的出发时间间隔，min；T运为列车在区间中的纯运行时间，min；I到发为列车到达车站至从车站出发的时间间隔，min；mi-j为车站i与车站j在该线路上的实际距离，km。

（2）动车组运用指标：N为动车组车底的最大取值；n为动车组车底索引，n∈N；ti(n)为编号为n的动车组车底从车站i出发的时刻；tj'(n)为编号为n的动车组车底到达车站j站的时刻表示动车组车底n ti(n)时刻从i站出发，在tj'(n)时刻到达j站；yi表示动车组是否在j站停车。

1.3 高速铁路列车运行图与动车组运用一体化模型

动车组运用的首要任务就是能完成给定的运行任务，在此基础上，区间运行线数量越多，高速铁路列车运行图与动车组运用一体化优化程度越优[6]。因此，在一体化优化模型中，通常采用区间线路数量最大为优化目标，即

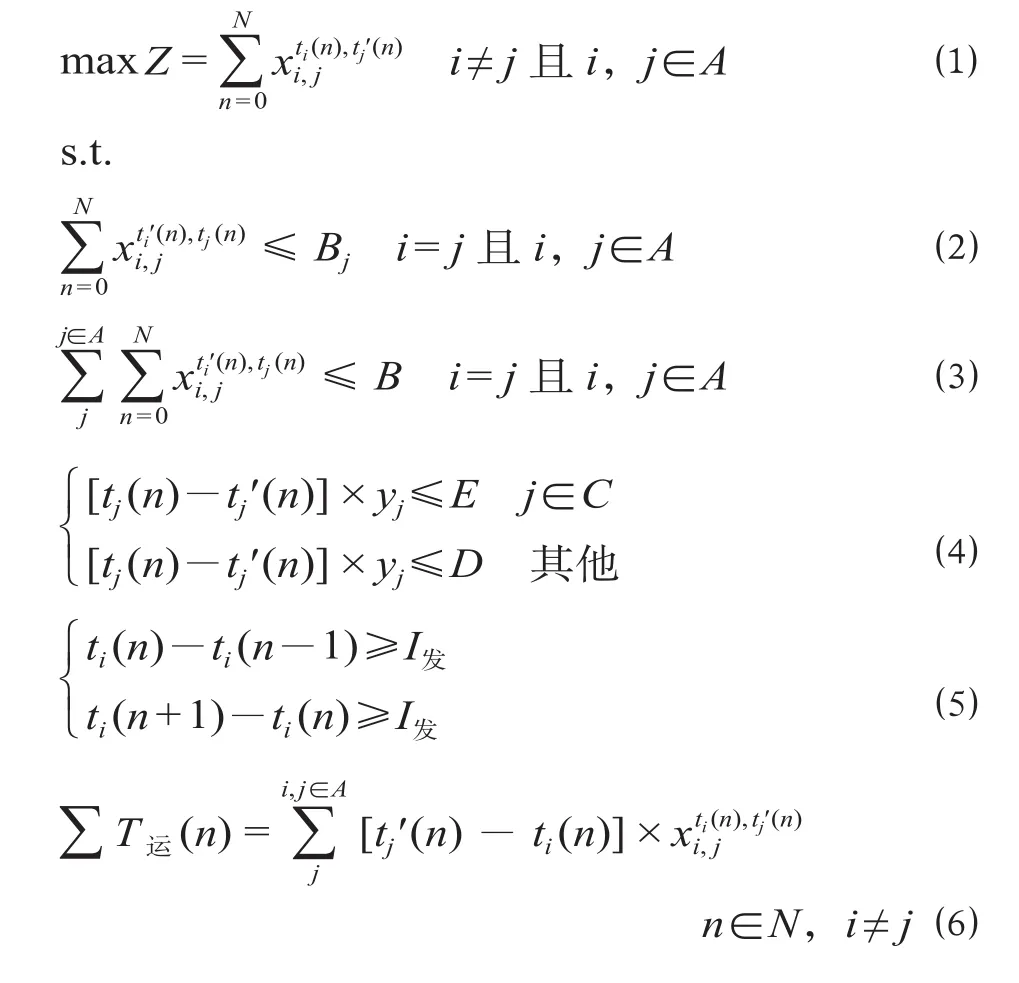
公式 ⑵ 表示所有的列车在j站的停站总次数不大于参数Bj，其中参数Bj随着j车站的不同而改变。公式 ⑶ 表示所有的列车在所有车站的停站总次数不大于参数B，其中参数B随着车站集的不同而变化。公式 ⑷ 表示列车在j站的停站时间，包括4种情况，即列车在终点站是否折返(折返时间标准是E)，以及列车在中间站是否停车(停站时间标准是D)，其中参数D，E随着车站的不同而发生变化。公式 ⑸ 表示避免列车的车站间隔时间小于最小间隔时间，即当列车的时空路径经过一个点时，与该点的间隔时间不满足最小间隔时间的相邻点都不能被其他的列车时空路径所占用[7]。公式 ⑹ 表示动车组车底n在车站间的纯运行时间之和。公式 ⑺ 表示动车组车底n的停站时间之和。公式 ⑻ 表示动车组车底n的总运行时间不可超过48 h。公式 ⑼ 表示动车组车底n的总运行公里数不超过4 000 km。此外，规定动车组在线路上运行的时间是6 : 00—24 : 00。

2 高速铁路列车运行图与动车组运用一体化优化模型求解

由于研究模型是单目标模型，包括多个车站，具有一定规模，为了验证高速铁路列车运行图与动车组运用一体化优化模型及求解方法的正确性和适应性，通过构建案例，运用GAMS软件对模型进行求解。

2.1 基础数据

假设线路i-j-k为双线铁路，专门用于高速铁路旅客列车运行。其中i表示动车段所所在站，j，k为普通高速铁路车站，线路i-j-k简化示意图如图1所示。

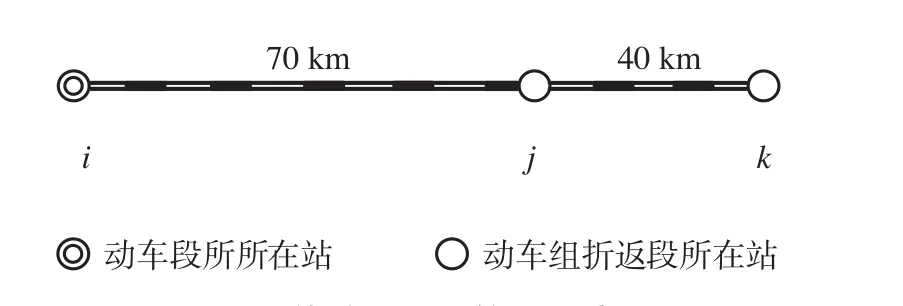
图1 线路i-j-k简化示意图Fig.1 Simplified schematic diagram of route i-j-k

动车组在中间站j站的停站时间标准为1 min；运用动车组数量为2组，i站共发送13列动车组，j站共发送10列动车组，k站共发送13列动车组；第1列动车组的发车时间为6 : 11；最后一列动车组的到达时间为23 : 57；列车的最小追踪间隔时间为80 min；动车组在终点站的最小停站时间为20 min。列车在区间的纯运行时间T运如表1所示。

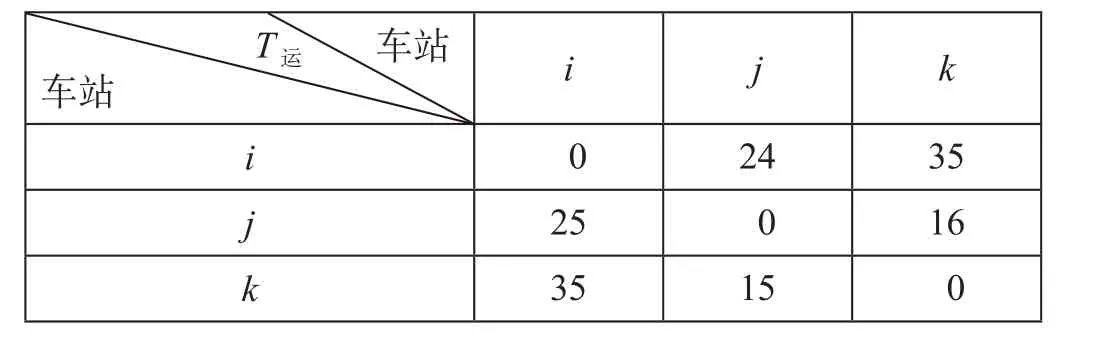
表1 列车在区间之间的运行时间T运 minTab.1 Train running time TYun in the section

满足上述要求的前提下，考虑实际旅客的出行需求，可以得出一个列车时刻表。根据列车时刻表可以编制出列车运行图，线路i-j-k的列车运行图如图2所示。根据图2给定的列车运行图，以及只能在车站i进行日常检修和定期检修的已知条件，得到动车组周转计划如图3所示。直接在列车运行图上勾画动车组运用方案如图4所示。

统计线路i-j-k上各车站的停站次数，i站为13次/d，j站为10次/d，k站为13次/d。

2.2 算例说明

根据实际情况，假设动车组在终点站的停站时间标准为15 min，即E= 15 min；动车组在中间站j站的停站时间标准为1 min，即D= 1 min；列车的追踪间隔时间为60 min，即I发= 60 min；第一列动车组的出发时间为6 : 11，即ti(1) = 6 : 11；考虑每天的天窗时间，仅以6 : 00—24 : 00时间段为例，用GAMS求解出线路i-j-k的列车时刻表。首次输入运用的动车组数量为2组；列车在该线路上车站i与车站j之间的距离mi-j为70 km，mi-k为40 km；列车在区间之间的运行时间T运如表1所示；设定列车在每个车站的总停站次数最大值i站为16次/d，j站为12次/d，k站为16次/d。

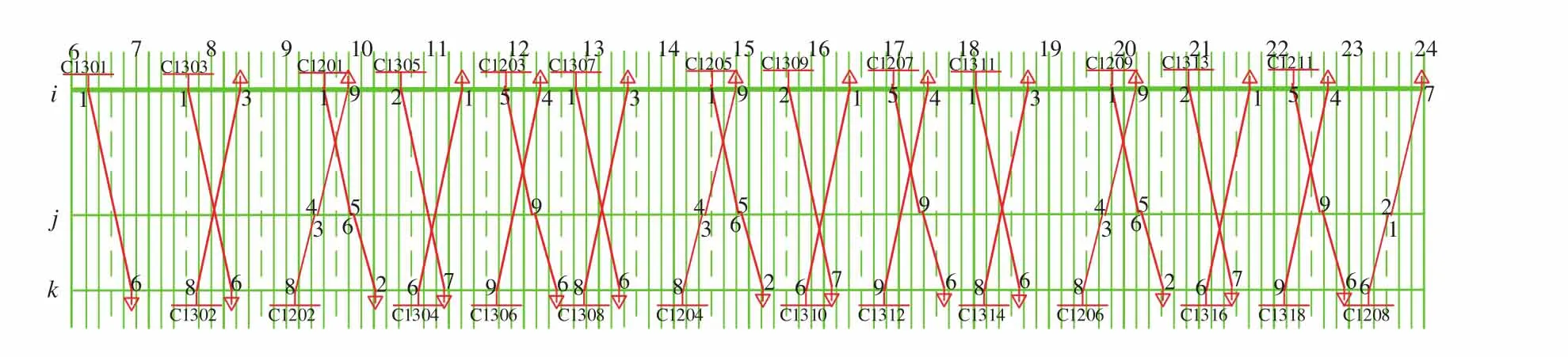
图2 线路i-j-k的列车运行图Fig.2 Train working diagram of route i-j-k

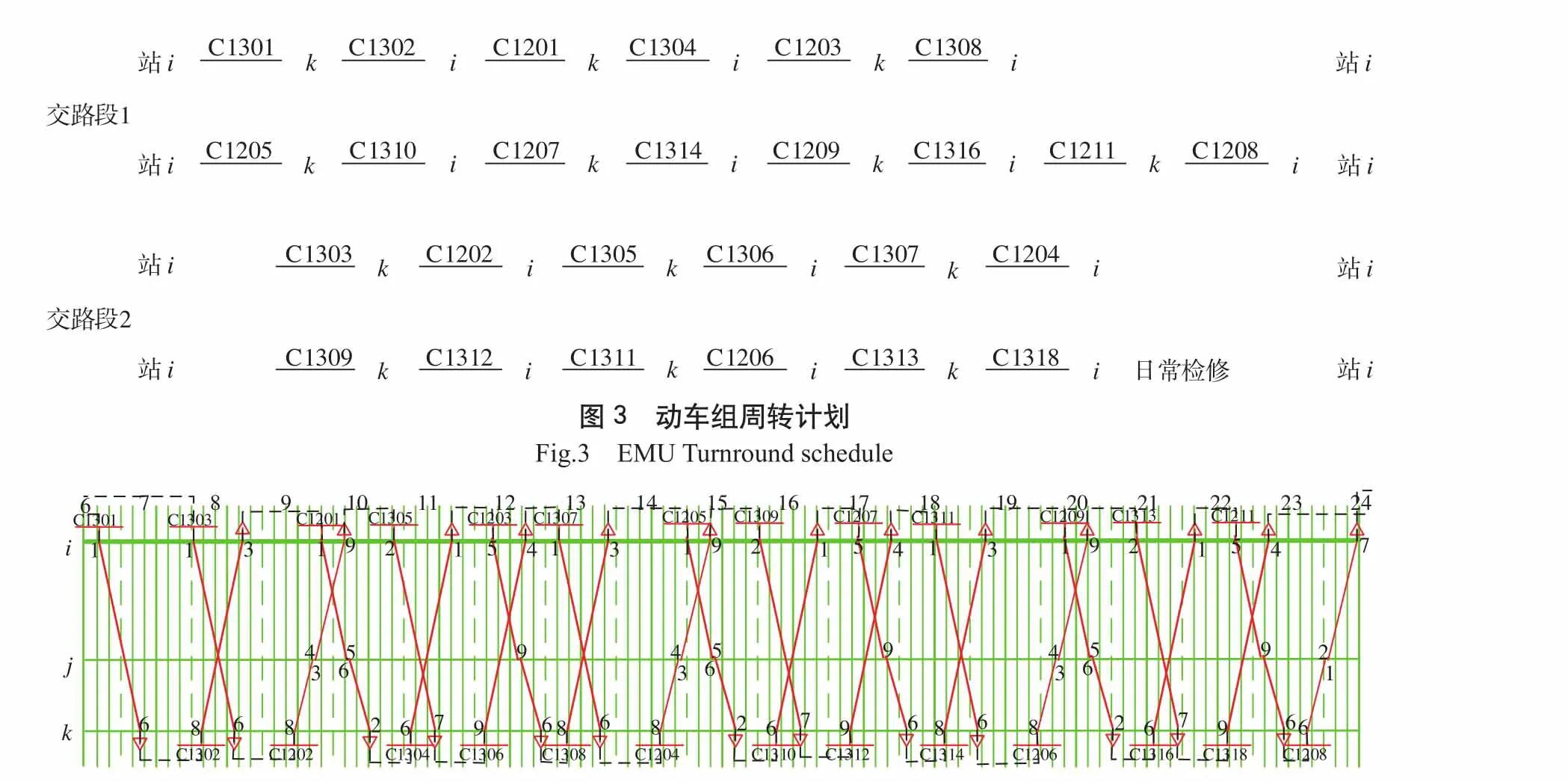
图4 动车组运用方案Fig.4 EMU operation plan

2.3 模型求解

编写GAMS程序代码，在GAMS软件运行以上模型，可求解得到结果。根据上述数据，可知运用动车组数量为2组，i站共发送16列动车组，j站共发送12列动车组，k站共发送13列动车组，可以满足实际情况。

当动车组数量减少为1组时，i站共发送10列动车组，j站共发送10列动车组，k站共发送10列动车组，其动车组运用方案(运用动车组数量为1组)如图5所示，不符合实际情况，即不可以满足i站共发送13列动车组，k站共发送13列动车组的实际情况。

由此输出当动车组为2组时的数据，即运用动车组数量为2组时，线路i-j-k的列车时刻表。将GMAS输出的表格铺画到十分格运行图上，得到动车组运用方案(运用动车组数量为2组)如图6所示。其中的动车组运行轨迹可构成高速铁路列车运行图(运用动车组数量为2组)如图7所示。

上述案例说明，可以运用GAMS软件编写代码[8]，求解线路i-j-k的高速铁路列车运行图与动车组运用一体化优化模型，并得到最优化方案[9]。

2.4 算例分析

京津城际全长120 km，共5个站，包括北京南、亦庄(未开通)、永乐(未开通)、武清及天津站。由于上述5个车站中亦庄和永乐站还未开通，因而在研究动车组运用时不予考虑，只考虑有列车到发作业的车站。北京南站有北京动车段、天津站有天津曹庄动车运用所，在此基础上，可以将京津城际进行简化，京津城际简化线路示意图如图8所示。

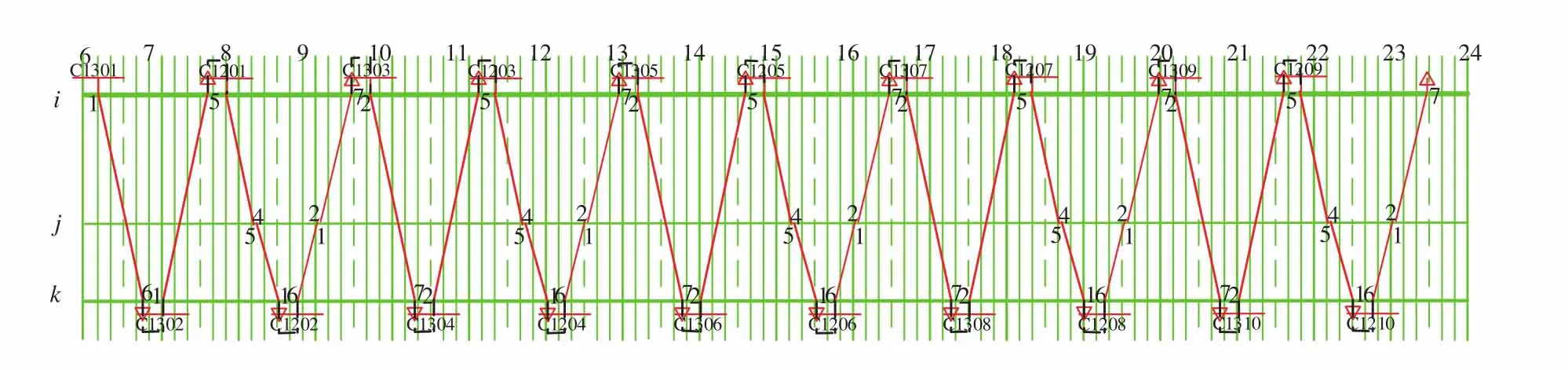
图5 动车组运用方案(运用动车组数量为1组)Fig.5 EMU operation plan (the number of EMU is 1 unit)

图6 动车组运用方案(运用动车组数量为2组)Fig.6 EMU operation plan (the number of EMU is 2 units)

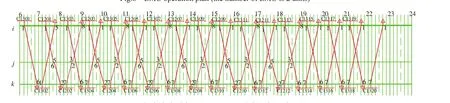
图7 高速铁路列车运行图(运用动车组数量为2组)Fig.7 High speed train working diagram (the number of EMU is 2 units)

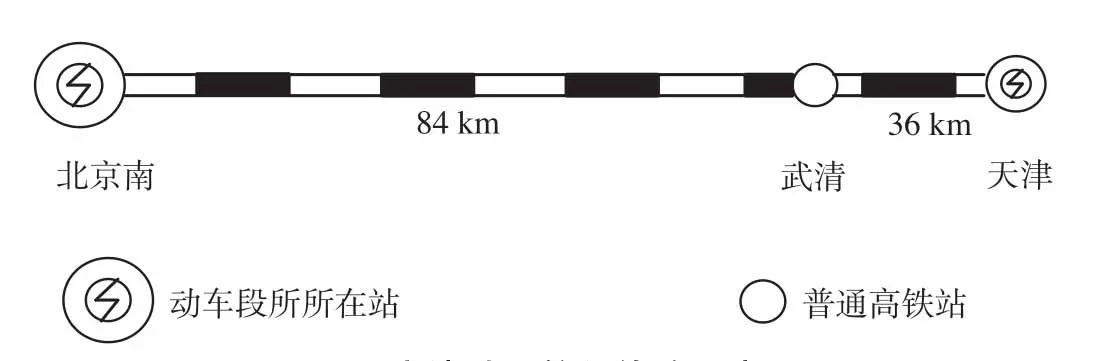
图8 京津城际简化线路示意图Fig.8 Simplified route schematic diagram of Beijing-Tianjin intercity railway

以京津城际为研究对象，可用动车组数量为9组，编写GAMS程序代码，并运行以上模型，可求解得到结果，即京津城际动车组运用方案(运用动车组数量为9组)如图9所示。北京南站共发送80列动车组，武清站共发送48列动车组，天津站共发送78列动车组。

比较目前京津城际实际列车运行图，在运用相同动车组数量的前提下，一体化优化方案可多发6列车，从而为实际列车运行图铺画提供一定参考。

3 结束语

随着我国社会经济快速发展，旅客出行需求逐年增加。目前，我国京沪(北京南—上海虹桥)、京广(北京西—广州南)等高速铁路繁忙干线运输能力逐步趋于饱和，同时每年需要投入大量资金增加动车组采购数量，对列车开行和动车组运用两者进行同步优化，以最少的动车组实现列车开行数量的最大化，对于提高运输能力、节约动车组运用、提升运输效率效益，具有重要的实用价值和社会经济效益。研究虽然构建了一体化模型，但受数据搜集、运算工具等条件限制，仅以京津城际为例进行了算例验证，后续一方面需要结合不同的路网规模、列车开行需求、客流需求、动车组类型等条件对模型进一步补充和完善，使之更加贴近高速铁路运营实际。另一方面，随着路网规模的扩大，计算过程将变得更加复杂，需要对算法进一步简化和深度优化，以取得较优的运算结果[10]。

图9 京津城际动车组运用方案(运用动车组数量为9组)Fig.9 EMU operation plan of Beijing-Tianjin intercity railway (the number of EMU is 9 units)