动车组运用作业调度问题研究

刘禹显，牛 丰

（1.铁道党校 研修培训中心，北京 100088；2.中国铁路总公司 办公厅，北京 100844)

0 引言

动车组在我国铁路旅客运输中得到广泛应用，我国高速动车组列车在旅客列车中的比重已超过50%。推进包括动车组运用在内的铁路运输组织和调度指挥智能化，是“十三五”期间我国铁路面临信息化的重要任务。目前我国铁路运输的实际生产操作中，动车组列车作业调度计划主要依靠人工经验制订，存在着环境适应性差、计划效率低等问题。因此，建立能够为相关信息系统开发奠定基础的优化方法具有重要意义。

目前在动车组运用方面的研究主要集中于动车组运用计划安排和动车组运用作业调度2个方面。前者主要关注动车组运用数量和循环运用；后者主要研究在日常运输组织过程中一定动车组资源的合理运用问题。一些学者将动车组运用计划编制转化成不考虑检修约束的指派问题和考虑动车组检修约束的(多)旅行商2类问题。由于我国路网和列车开行数量规模较大，因而在求解时常采用启发式算法，包括基于概率的局域搜索算法、蚁群算法、模拟退火算法、遗传算法、大规模邻域搜索算法[2-4]，以及采用列生成法等精确算法求解[5]。在国外，Lin等[6]、Cacchiani等[7]分别采用分枝定界和拉格朗日松弛方法求解动车组运用作业调度问题。

动车组运用作业调度(Train Unite Scheduling Problem，TUSP)是以列车运行图中各列车始发终到时间关系和可使用的动车组资源为基础，结合运输组织实际情况[8]，特别是动车组状态约束、动车组类型约束、动车组运用接续条件约束，有效降低动车组接续成本，对动车组日常运用方案进行合理安排的问题。研究基于TUSP问题和列车运行图之间的关系，构建混合整数规划模型，并采用模拟退火求解算法，通过高速铁路网络实际算例进行分析。

1 TUSP问题描述与模型构建

TUSP问题通常以在给定列车运行图和动车组资源条件下，确定出每一动车组所需担当车次及其顺序的合理方案，以实现最低动车组接续成本最小化的目标。同时，TUSP问题还需满足下列要求。①可使用动车组资源的运用时间范围：每个动车组可被运用的时间范围是全日列车运行图的运营时段。②动车组状态约束： 每个动车组投入运用的起始空间位置已知，动车组状态由运用作业调度方案决定。③动车组类型约束：每个车次的担当动车组类型符合要求。④动车组运用接续条件约束：每个动车组担当的相邻车次间满足接续时间要求。根据上述描述，TUSP问题的集合、参数和变量定义如下。

1.1 符号定义

车站集合S = {1，2，…，l}；列车运行图车次集合为T = {1，2，…，n}；动车组运用的车次集合T' = {0，…，n + 1}，其中0和n + 1是虚拟车次，0为所有动车组的起始虚拟车次，n + 1为动车组的终止车次，即每个动车组的运用工作必须从0开始，以n + 1结束；可用动车组集合D = {1，2，…，m}；车次i的类型要求为TRi，i ∈ R；车次i的始发终到时刻分别为REi和RLi，i ∈ R；动车组k的类型为DCk，k ∈ D；动车组k从车次i接续车次j的成本为 Cijk，i，j ∈ T'，k ∈ D，Cijk包括列车始发终到站和始发终到车站位置相关的接续成本，包含接续时间成本Tijk、异地接续空驶成本dijk两部分，计算公式为Cijk= Tijk+ Mdijk，其中M为动车组回送的权重系数，可取为一个很大的常数；车次i与车次 j间的接续时间为 Tij，i，j ∈ T'，k ∈ D，其与车次i的终到时刻和车次j的始发时刻有关；动车组整备时间为P。

1.2 决策变量和模型建立

引入动车组的车次担当次序变量xijk和动车组的车次接续关系变量。其中，若动车组k (k ∈ V)先担当车次i再接续担当车次j，则xijk= 1，否则xijk= 0；若车次i与车次j由某一动车组担当，并存在接续关系，则yij= 1，否则yij= 0。将xijk和yij作为求解动车组运用作业调度方案的决策变量，以最小化接续成本为目标，建立TUSP问题的优化模型如下。

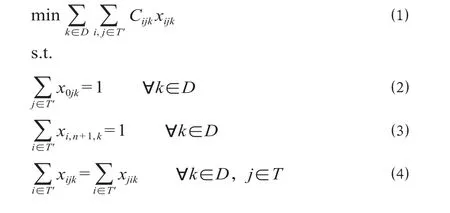
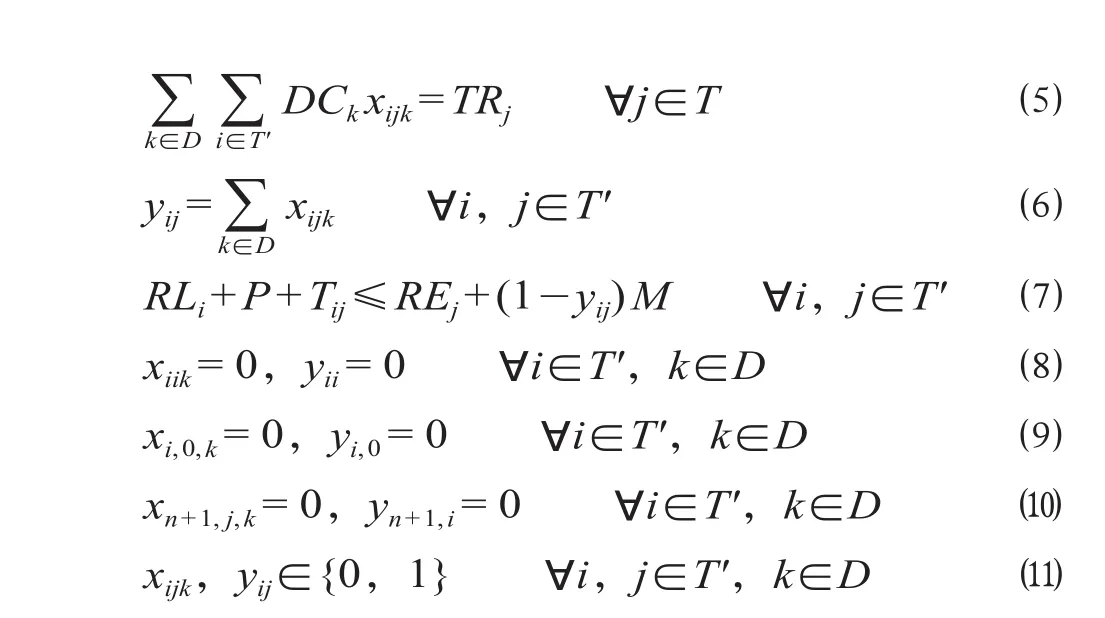
其中，公式 ⑴ 为最小化接续成本的目标函数。公式 ⑵—⑸ 为动车组状态约束：公式 ⑵—⑶ 表示每一动车组从担当车次0开始到车次n + 1结束；公式⑷ 表示每一动车组担当车次存在紧前紧后的守恒关系；公式 ⑸ 为 yij与 xijk间的关系。公式 ⑹ 为动车组类型约束，也即执行车次j的动车组类型与该车次所需车型需求相匹配；公式 ⑺ 为动车组运用接续条件约束，即当车次i、车次j间存在紧前紧后接续关系时，担当车次j的开始时刻不能早于车次i的完成担当时刻加上整备时间和接续时间。公式 ⑻—⑾为变量的取值约束，其中公式 ⑻ 表示若i = j，则xiik和yii为0，即动车组运用不存在重复车次；公式 ⑼ 表示0车次不存在紧前车次；公式 ⑽ 表示n + 1车次不存在紧后车次；公式 ⑾ 表示任何xijk和yij的0-1变量取值约束。

上述TUSP模型是一个混合整数规划，以动车组接续成本最小化作为优化目标，约束条件全面考虑了动车组运用作业调度的各项要求，使得模型的解能够满足动车组运用作业调度的实际需求。

2 基于车次顺序的模拟退火算法

由于TUSP较为复杂，属于NP-hard问题，现有商用软件很难在可控时间内完成实际规模问题的求解，因而采用模拟退火算法求解。模拟退火(Simulated Annealing，SA)算法最早由Ward等[9]引入组合优化领域。这一算法是一种局部搜索算法，但能以一定概率接受一个劣解，从而有效避免陷入局部最优。

2.1 基于车次顺序列表的构解方法

将动车组运用作业调度方案表示为一个车次顺序列表。根据列车运行图车次集合T，随机生成一组包含1-n的车次顺序列表T_list。例如，当列车集合有10个车次时，车次列表T_list为一包含1—10的列向量 (5，7，8，9，2，10，3，6，1，4)。

在车次顺序列表中，一个动车组担当车次的范围从上一动车组担当车次之后一车次起，至在运营时间内，满足各项约束条件，可担当车次止的一个连续的车次顺序列表片段。

2.2 动车组运用作业调度方案目标计算

根据动车组运用作业调度方案和车次顺序列表对应关系，其目标函数值计算流程如下。

（1）按照车次顺序列表T_list顺序选取分配的车次i。

（2）可用动车组列表D_list生成。校验动车组集合D中车辆k空闲时间段与车次i所需起止时间段是否匹配。如果有满足上述条件的匹配，则将该车次存入可用动车组列表D_list。

（3）动车组任务指派。选取D_list中满足车次i的动车组类型需求的调运成本最低动车组组合，将对应动车组时间段安排车次i。

（4）更新动车组任务安排状态。将D_list中被分配动车组在车次i起止时间状态更改为被占用。

（5）调运成本计算。待任务列表中所有车次都分配完毕，计算所使用的动车组的接续成本，得到目标函数值。

2.3 解的扰动策略和接受机制

采用随机置换方法对当前车次顺序列表进行扰动，即在当前任务列表中随机选2个车次位置id_1与id_2，交换2个车次位置D_list (id_1)与D_list (id_2)。例如，随机选择到2.2节中车次顺序列表的第3位与第6位，置换对应位置的车次后，新的车次顺序列表变为(5，7，10，9，2，8，3，6，1，4)。

由于优化模型属于最小化问题，若Δf＜0，则接受新车次顺序列表以及所求得的新解；若Δf≥0，则采用Metropolis接受准则，即计算接受概率exp (-df / T )，若大于(0，1)之间的随机数rand，则同样接受新车次顺序列表及新解；否则保留当前车次顺序列表及当前解。

2.4 模拟退火冷却进度表和终止规则

冷却进度表影响模拟退火算法的性能，其包括初始温度T0，结束温度Tend，冷却速率r，Markov链长L。

2.5 算法框架和求解步骤

根据以上算法设计思想，基于车次分配列表的模拟退火算法框架如图1所示。

图1 模拟退火算法框架图Fig.1 Algorithm framework of SA

模拟退火算法的步骤如下。

步骤1：初始化参数，设定初始温度T = T0。

步骤2：随机生成各动车组担当车次顺序的初始列表T_list，并计算目标函数f (T_list)。

步骤3：扰动产生各动车组担当车次顺序的列表T'_list，重新计算目标函数f (T'_list)。

步骤4：判断目标函数是否更优，若是，则接受新车次列表与新解；否则按Metropolis准则以一定概率接受新车次列表与新解。

步骤5：判断是否达到迭代次数，若是，则执行步骤6；否则执行步骤3。

步骤6：降温过程，以一定速率进行冷却退火。

步骤7：判断是否达到终止条件，若是则输出解；否则执行步骤3。

3 算例分析

3.1 算例数据

为了验证所设计的基于任务列表的模拟退火算法对TUS问题的求解效果，选择我国中东部高速铁路网络和列车运行图数据进行仿真实验，我国中东部高速铁路网络如图2所示。可用动车组集合的信息如表1所示，需要承担列车运行图上26个车次的担当任务，各车次所需动车组类型、始发站、终点站及始发终到时刻等列车运行图信息如表2所示。

考虑到算例规模，所采用的模拟退火算法参数为：T0= 1 000，Tend= 0.001，r = 0.95，L = 100。这些参数可使Metropolis接受概率在高温状态接近

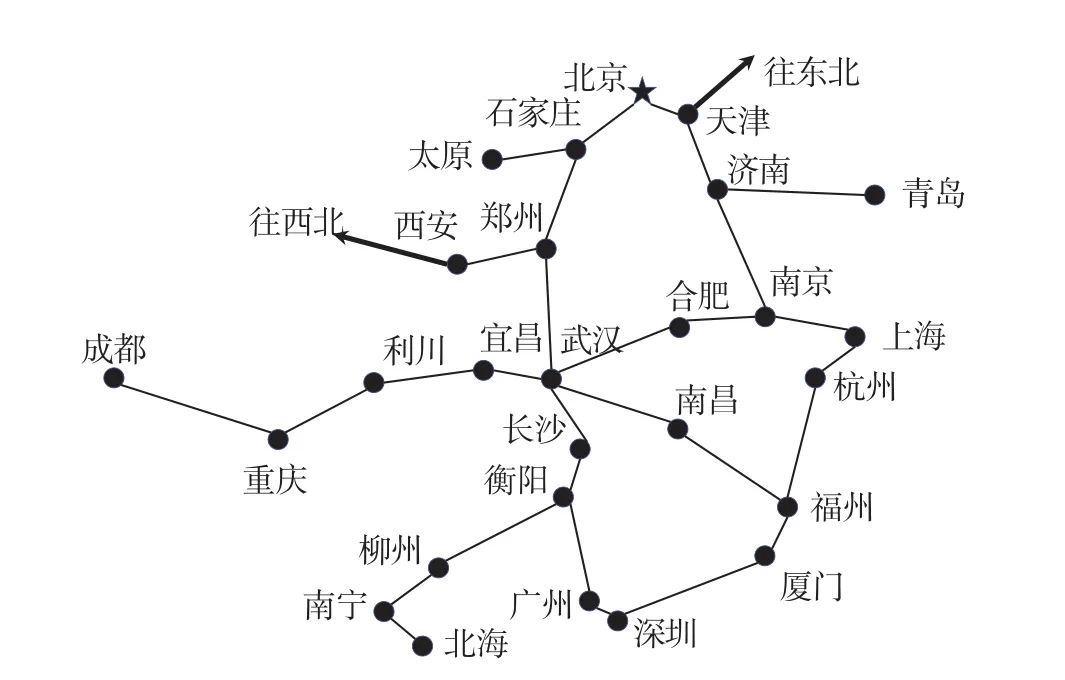
图2 我国中东部高速铁路网络Fig.2 High-speed railway network in Central and East China

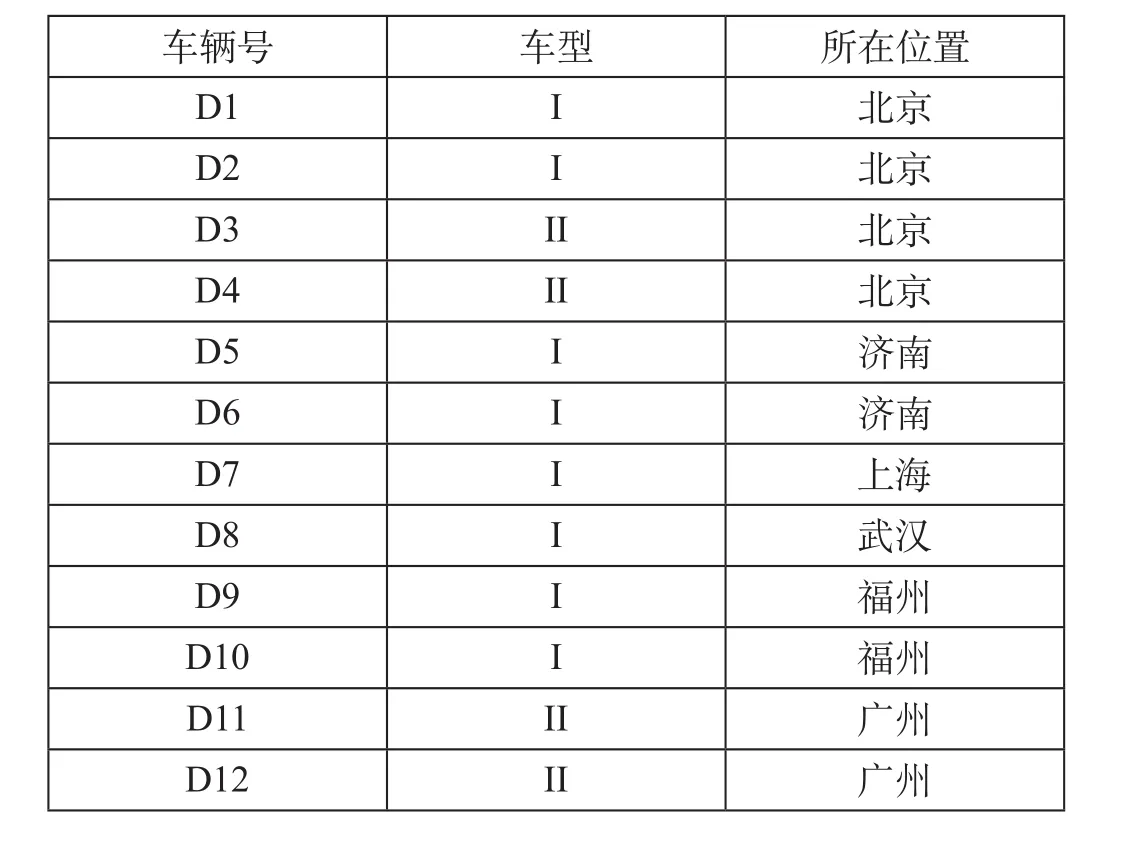
表1 可用动车组集合的信息Tab.1 Available EMU groups information

1，在低温时概率接近0，符合模拟退火算法的收敛要求。

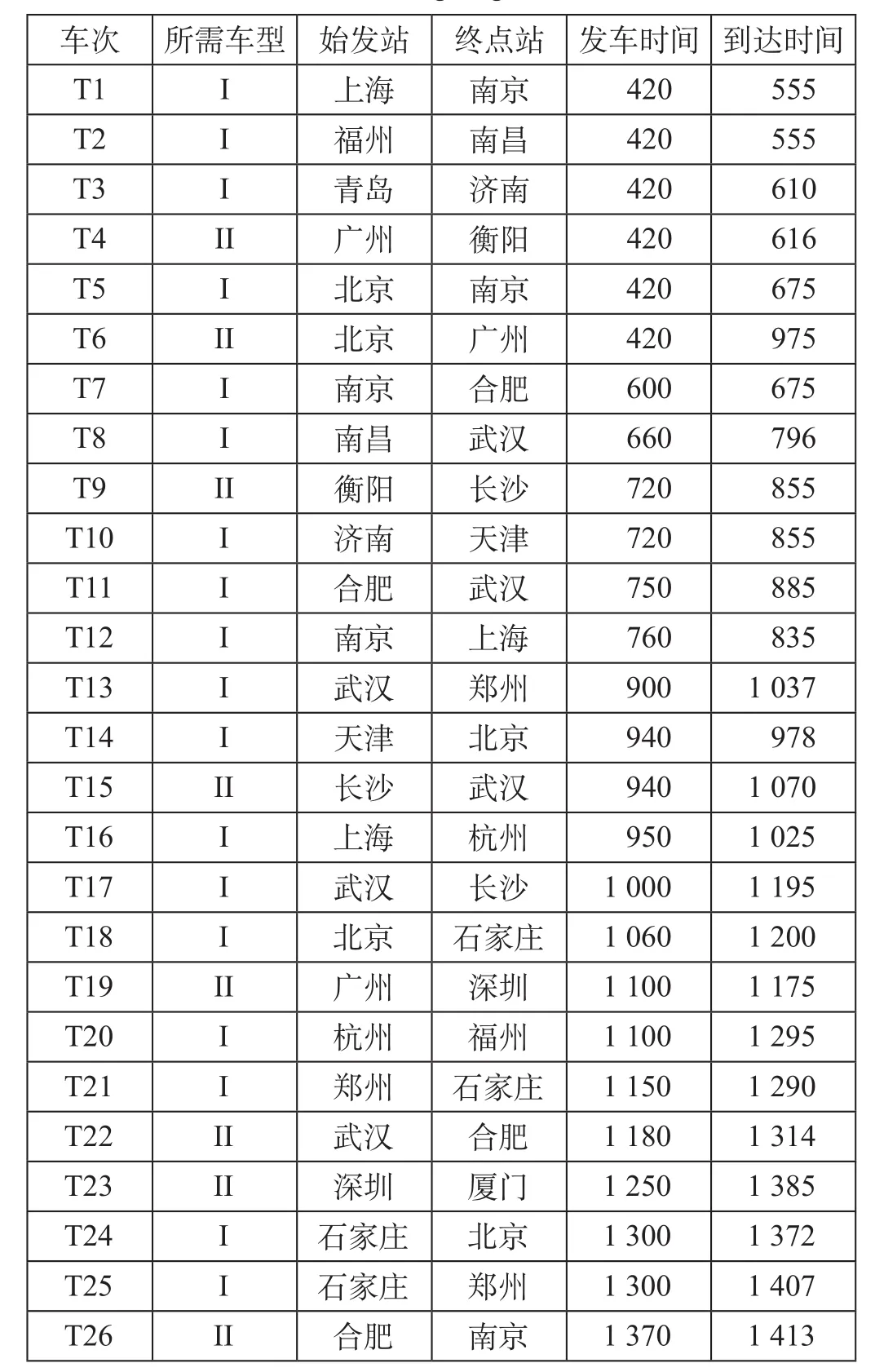
表2 列车运行图信息Tab.2 Train working diagram information

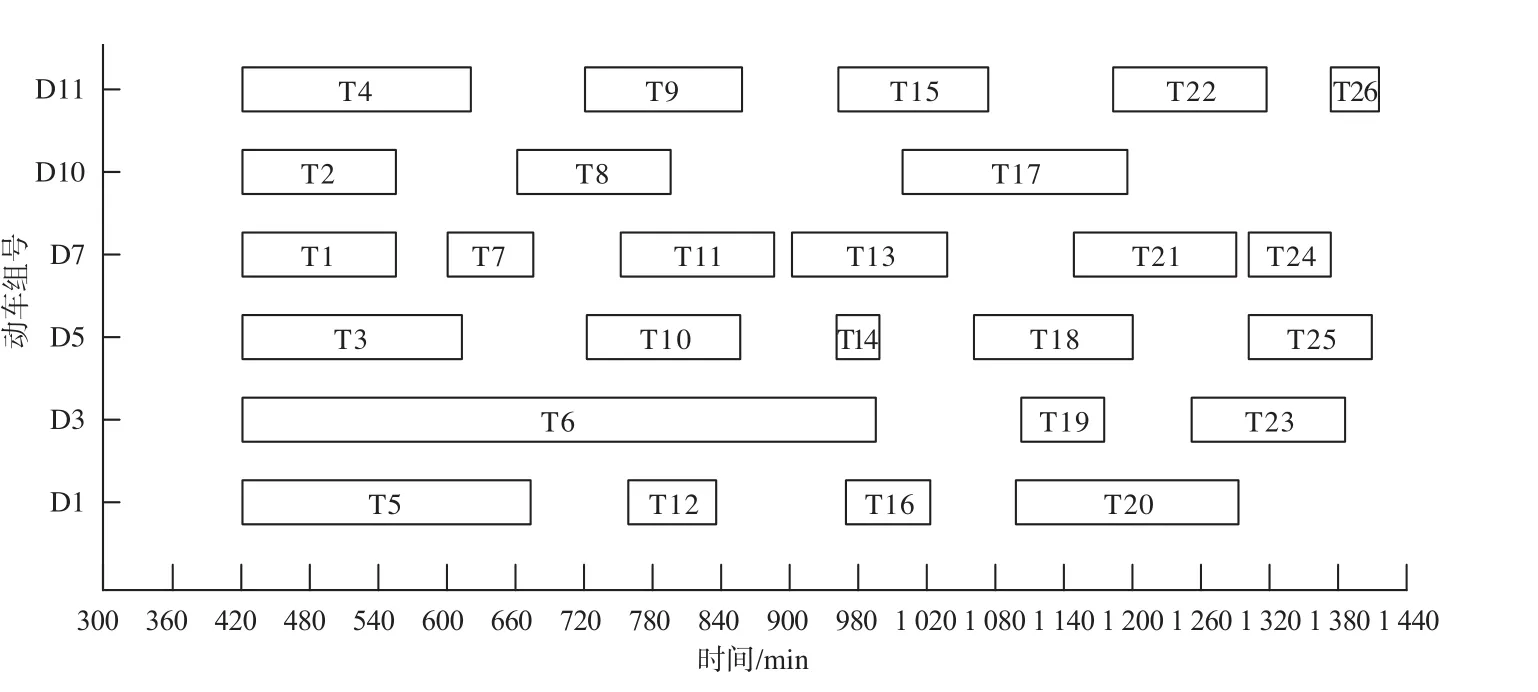
图3 动车组运用作业调度优化方案的甘特图Fig.3 Gantt chart of EMU operation scheduling optimization

3.2 算例结果

根据算例数据和算法参数，利用基于车次顺序列表的模拟退火算法求解。优化方案需使用动车组6列，即D1，D3，D5，D7，D10，D11， 动车组运用作业调度优化方案的甘特图如图3所示。在优化方案中，D5为济南—青岛间异地接续，其他均为本地接续。各动车组完成当日运用任务后，可依据所处位置进行下一日运用作业调度安排。

4 结束语

动车组运用作业调度问题是高速铁路运输组织研究的重要问题。由于动车组运用作业调度问题是一个复杂的组合优化问题，无论在理论上还是实践中都难以得到精确最优解。通过对列车运行图和动车组作业调度计划之间关系的分析，将其归结为以最小化接续成本为目标的混合整数规划模型，并设计了一种基于车次顺序列表的模拟退火算法对该问题进行求解。利用我国中东部区域部分高速铁路列车实际数据进行仿真实验，优化结果表明算法可以有效解决动车组运用作业调度方案制订问题。研究所建立的优化模型和优化算法具有较好的可拓展性，对更大规模的路网和更多高速铁路车次的实际问题同样适用，能够为动车组运用调度工作提供高效的决策支持。但是，由于我国高速铁路网络存在多种类型动车组运用的实际情况，下一步研究工作可以通过模型和算法的扩展，使之能够适用于多种类型动车组列车等更复杂情形。