聚酯纤维FRP加固钢筋混凝土梁抗弯性能
赵良科 黄 靓,* 曾令宏 许 颀 许仲远 高 畅
(1.湖南大学土木工程学院,长沙 410082; 2.中机国际工程设计研究院有限责任公司,长沙410021; 3.广州地铁设计研究院有限公司,广州 510010)
0 引 言
FRP(Fiber Reinforced Plastics)加固钢筋混凝土结构是目前土木工程学术研究领域和建筑业工程应用领域的重要方向之一。FRP材料具有抗拉强度高,密度小,耐久性好,耐腐蚀性强,热膨胀系数低等特点[1-3],并已应用于工程实例,美国、日本、欧洲等国已有相关FRP加固规范[4]。1982年,在瑞士联邦材料实验室首次进行了碳纤维增强塑料(Carbon Fiber Reinforced Plastics)加固钢筋混凝土的试验研究,开启了FRP在结构领域发展的序幕。随后玻璃纤维增强塑料(Glass Fiber Reinforced Plastics)等其他FRP材料在结构加固方面的研究也逐渐开展,并取得了诸多成果。BrenA S F等[5]和Alagusundaramoorthy P等[6]均对CFRP加固钢筋混凝土梁的抗弯性能进行了研究。结果表明:CFRP加固能够明显增强钢筋混凝土梁的承载能力。徐志胜[7]采用CFRP加固,明显提高了构件的承载力,单层与双层加固梁承载力相比对比梁能够分别提高15%和26%。吴刚[8]研究了CFRP加固混凝土梁的抗弯和抗剪试验。研究发现,钢筋混凝土梁经CFRP加固后,梁截面应变仍符合平截面假定,并且CFRP加固能够在一定程度上提高梁的抗剪承载力。甘贤军[9]采用GFRP加固混凝土梁。结果表明,梁裂缝发展缓慢,刚度和延性均有较大提高。Bahn B Y等[10]对CFRP和GFRP加固钢筋混凝土梁进行了端部锚固,试验表明:端部锚固能够有效地避免纤维布的端部剥离破坏,从而更加充分地利用纤维布的加固效果。
FRP加固混凝土梁是目前工程应用较广泛的加固方法之一,其破坏有弯曲破坏、剪切破坏、粘结破坏。为充分发挥FRP材料的优异性能,在采用FRP加固时,一般会避免加固梁出现剪切破坏和粘结破坏,Sebastian W M[11]通过研究粘结破坏模式及其影响得出粘结破坏为脆性破坏。这种粘结破坏没有破坏征兆,而且不能达到适筋破坏梁的承载力,甚至低于未加固梁的承载力[12]。因此FRP加固梁的承载力一般是指梁弯曲破坏时的承载力。基于以上分析,本文对聚酯纤维增强塑料(PFRP)加固钢筋混凝土梁常见的弯曲破坏模式进行了分析,并推导出了抗弯承载力计算公式。
目前采用的FRP加固材料主要为CFRP、GFRP等。这些FRP材料虽然有优异的物理力学性能,但其基体为树脂,且生产成本较高,并为不可再生材料。其中,碳纤维材料主要由日本生产,美国其次,其他国家产量很少,碳纤维国产化还有很大难度[13-15]。因此,传统的人造纤维在大规模推广应用方面有很大不足,并且不符合国家节能环保的要求。聚酯纤维(Polyester Fiber)是新型的人造纤维,是一种绿色可再生材料。聚酯纤维织物适用于衣着、室内装饰织物和地毯等方面。2009年,世界聚酯纤维产量3 190万吨[16],2010年,世界聚酯纤维产量为3 730万吨[17],2015年聚酯纤维产量达到5 800万吨。因此聚酯纤维的来源十分广泛。PFRP尽管在力学性能方面不及CFRP和GFRP,但因其较高的性价比以及良好的物理力学性能使之能够在结构加固中起到重要作用[18]。本文通过试验研究了PFRP加固混凝土梁的抗弯性能,同时将承载力试验值与理论值进行了对比。
1 PFRP轴向拉伸材性试验
用湿粘法分别制作4层和6层聚酯纤维布试件。每组5个试件,共10个。试件总长度170 mm,试件测试长度90 mm。在构件成型后并进行拉伸试验开始前,量取试件的厚度和宽度。
环氧树脂相对于聚酯树脂和乙烯基树脂而言,其拥有良好的力学性能和化学耐久性,固化收缩率较小且与纤维之间粘结性能好。因此,本试验的胶粘剂采用湖南固特邦土木技术发展有限公司研发的JN-C3P改性环氧胶粘剂。其物理和力学性能如表1所示。
表1环氧树脂的物理和力学性能

Table 1Physical and mechanical properties of the epoxy adhesive
PFRP轴向拉伸材性试验在湖南大学建材试验室进行,采用型号为C43.304的MTS微机控制电子万能试验机进行试验。加载时,采用位移控制的加载方式。加载速率为0.05 mm/min。在试验过程中,当施加的荷载达到极限荷载的60%~70%时,试件开始出现断断续续的轻微响声。随着荷载的不断增大,响声也逐渐增大且连续不断,直至试件发生断裂。试件拉断时,纤维布断裂成几条,并伴有清脆的撕裂声,断裂位置基本位于试件中部。通过试验得到的PFRP试件拉伸强度、弹性模量和断裂伸长率见表2。PFRP试件的应力应变曲线见图1。
由表2可知,4层和6层PFRP试件的拉伸强度平均值分别为42.9 MPa、44.3 MPa,弹性模量平均值分别为6.6 GPa、6.5 GPa,断裂伸长率为1.7%左右。
表2PFRP拉伸试验结果

Table 2Tensile test results of PFRP
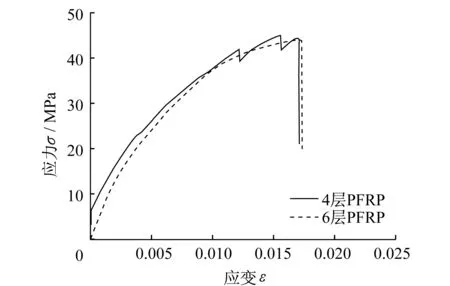
图1 PFRP应力-应变曲线Fig.1 Tensile stress-strain curves of PFRP
2 PFRP加固梁弯曲破坏模式及承载力分析
外贴FRP加固钢筋混凝土梁的破坏模式主要有以下几种类型:①FRP被拉断;②受压区混凝土压碎;③FRP纤维布剥离破坏;④梁底混凝土保护层剥离破坏;⑤梁斜截面剪切破坏。其中,①②属于弯曲破坏,③④属于剥离破坏,⑤属于剪切破坏。
如果在FRP加固钢筋混凝土梁的端部进行可靠的锚固,那么FRP加固梁的承载能力极限状态将主要取决于FRP被拉断或受压区混凝土压碎。剥离破坏主要是因为材料质量或施工质量不过关而引起的。本文采用的PFRP的抗拉强度远远小于CFRP,并且保证了材料质量和施工质量。因此,PFRP加固钢筋混凝土梁最常见的弯曲破坏模式主要有以下2种:①PFRP未拉断,受压区混凝土被压碎;②PFRP被拉断,受压区混凝土未压碎。
本文中所有材料性能均采用《混凝土结构设计规范》(GB 50010—2010)[19]中的有关规定。
文中,h为梁截面高度,b为梁截面宽度,h0为受拉钢筋合力作用点到梁受压边缘的距离,as为受拉钢筋合力作用点到梁受拉边缘的距离,x0为梁截面中和轴高度,εcu为混凝土极限压应变(本文取0.003 3),εc为混凝土压应变,εs为受拉钢筋应变,εf为PFRP纤维布应变,C为梁受压区混凝土合力,Es为受拉钢筋弹性模量,Ef为PFRP纤维布弹性模量,Ts为受拉钢筋合力,Tf为PFRP纤维布合力,fc为混凝土抗压强度,fy为受拉钢筋的屈服强度,As为受拉钢筋横截面积,Af为PFRP纤维布横截面积,Mu代表梁横截面弯矩。
2.1 破坏模式(1)
当PFRP加固钢筋混凝土梁的钢筋和PFRP配置量适中时,可能会发生PFRP未拉断,受压区混凝土被压碎的破坏模式。此时,εf<εfu,εc=εcu,εs≥εy。截面的应力-应变图如图2所示。
由平截面假定得:
εcu
(1)
受压区混凝土合力可采用等效的矩形应力图来进行计算,根据《混凝土结构设计规范》(GB 50010—2010)[19],α1=1.0,β1=0.8。
由轴向方向力的平衡可得:
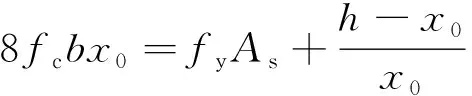
(2)
式(2)为关于x0的一元二次方程,可求解出混凝土梁截面中和轴高度x0,进而可求解出εf。因而可得此破坏模式下,PFRP加固钢筋混凝土梁的极限承载为

图2 破坏模式(1)应力-应变图Fig.2 Stress-strain distribution of failure mode (1)
(3)
2.2 破坏模式(2)
当PFRP加固钢筋混凝土梁的钢筋和PFRP配置量较少时,可能会发生PFRP被拉断,受压区混凝土未压碎的破坏模式。此种破坏模式下,截面的应力-应变图如图3所示。此时,εf=εfu,εs≥εy。由平截面假定得:
(4)
由轴向方向力的平衡可得:
α1β1fcbx0=fyAs+ffAf
(5)
文献[20]根据混凝土本构关系推导出了此种破坏模式下任意εc所对应的α1和β1的值,并绘制成了速查表。
先将x0赋值,根据式(4)计算出εc,然后根据速查表查出α1和β1的值,并将α1和β1代入式(5),判断等号两边是否相等。若相等,则此时x0即为所求值;若不相等,则不断调整x0,重复上述计算,直至等号两边相等为止,即可求出x0。求出x0后,可得PFRP加固钢筋混凝土梁的极限承载力为:
(6)

图3 破坏模式(2)应力-应变图Fig.3 Stress-strain distribution of failure mode (2)
3 PFRP加固钢筋混凝土梁抗弯试验
3.1 试验概况
本试验测试了3根试件梁。试件梁底粘贴PFRP进行加固。加载方式为四点弯曲加载。试件详细信息如表3所示。加载装置如图4所示。钢筋的材料特性如表4所示。
3.2 加载及破坏
在钢筋屈服前采用荷载控制的加载方式,加载速率为5kN/级。钢筋屈服后,采用位移控制的加载方式,加载速率为2 mm/级。试验中,3根试件梁的弯曲裂缝开展过程基本相同。加载初期,整个试件梁处于弹性工作状态,钢筋、混凝土、PFRP协同工作。加载至0.25Pu时,跨中梁底开裂,受拉区混凝土失去作用。随着荷载的不断增大,裂缝逐渐开展,并伴有新的裂缝产生。加载至0.5Pu时,受拉钢筋屈服。继续加载,加固梁PFRP时而出现细微响声。最终B-1的破坏模式为竖向裂缝过宽,不满足《混凝土结构设计规范》(GB 50010—2010)[19]第3.4.5条的要求。B-2出现清脆响声,破坏模式为PFRP被拉断。B-3破坏模式为受压区混凝土被压碎。
表3试件参数

Table 3Details of specimens

图4 试验加载装置Fig.4 Test Setup
表4钢筋物理力学性能

Table 4Material properties of steel bars
4 试验结果与分析
4.1 验证平截面假定
平截面假定是钢筋混凝土梁理论分析中被广为接受的基本理论之一。本文中PFRP加固混凝土梁的承载力计算即在平截面假定的基础上进行的。因此,验证平截面假定是十分必要的。本文在钢筋混凝土梁侧等间距布置了5个应变片,用来监测混凝土应变,部分荷载等级下试件的混凝土应变情如图5所示。

图5 梁侧混凝土应变分布图Fig.5 Concrete strain distribution diagram
由图5可知,试件梁在加载时,混凝土应变与截面高度基本接近于一条直线,因此试件梁符合平截面假定,因而可采用理论推导的计算公式进行预测PFRP加固梁的承载力。
4.2 承载力分析
试件梁的抗弯极限承载力如表5所示。其中,Pu代表承载力试验值,Pp代表承载力预测值。根据不同的破坏模式选取相应公式预测其抗弯承载力。从表5可知,承载力预测值比试验值略小,因而采用本文中公式计算PFRP加固梁的抗弯承载力是安全的,并且是合理可行。由于PFRP、混凝土等试验参数有一定误差,因此承载力理论计算值与试验值有一定误差属于正常现象。此外,B-1承载力相比于对比梁CB-1提高了22.3%,B-2承载力相比于对比梁CB-1提高了23.9%。因此,采用PFRP加固能够提高钢筋混凝土梁的承载能力。
表5
试件破坏模式及抗弯承载力理论值与计算值对比

Table 5Failure modes and comparison between calculation values and experiment values of bending capacity
未配置FRP的梁CB-1破坏模式为竖向裂缝过宽,不满足《混凝土结构设计规范》[19]中的规定。虽然这种破坏模式属于适筋延性破坏,但CB-1的延性性能较差,并且跨中挠度较低,裂缝间距也较大,因此其耗能能力较差。对于B-1来说,其破坏模式为PFRP被拉断,类似于少筋破坏。虽然其最终破坏模式并不满足延性破坏的要求,但相比于CB-1,其破坏过程中的竖向裂缝宽度大为减小,并且裂缝更加密集,裂缝间距较小,跨中挠度有较大增加,表现出更好的耗能能力和延性发展的能力。因此B-1虽为脆性破坏,但其破坏前的延性发展更为明显,抗弯性能也得到了很大提高。在工程应用中,关于梁破坏模式的设计有相关的规定,但对于FRP加固梁来说,也应注重其破坏前的性能提高。因此,对于PFRP加固梁,应设计成综合性能最优的梁B-2。
此外,对于B-1来说,因为本试验采用了较高强度的混凝土,因而采用4层PFRP加固钢筋混凝土梁的破坏模式为PFRP被拉断,此种破坏模式虽属于弯曲破坏,但由于其破坏表现出明显的脆性,应用中应避免出现这种破坏模式。钢筋混凝土梁的配筋率对其延性有着很大的影响。配筋率越高,梁延性越小,此时采用PFRP加固,PFRP变形较小,因此PFRP可在保持部分塑性的同时发挥其强度。因此,当采用4层PFRP加固时,为防止发生PFRP被拉断的脆性破坏,应适当提高钢筋混凝土梁的配筋率或用于加固较低混凝土强度钢筋混凝土梁。除此之外,还可适当增加PFRP的层数,以避免出现脆性破坏,如B-2所示。
5 结 论
本文对PFRP进行了轴向拉伸材性试验,并通过试验研究了PFRP加固钢筋混凝土梁的抗弯性能,推导出了PFRP加固钢筋混凝土梁常见破坏模式下的承载力计算公式。根据本文分析,可以得出以下结论:
(1) PFRP的轴向拉伸性能较为稳定,离散性小。
(2) PFRP加固梁的梁侧混凝土应变符合平截面假定。
(3) PFRP加固能够提高钢筋混凝土梁的抗弯承载力。4层PFRP加固能够提高22.3%,6层PFRP加固能够提高23.9%。
(4) PFRP加固梁极限荷载试验值与理论值较为吻合,并且偏于安全。同时对PFRP加固钢筋混凝土梁的设计提出了建议。

