长周期地震动作用下高层结构地震反应的对比研究
蒋连接 白国良 蔡万军 巩思锋
(1.宿迁学院建筑工程学院,宿迁 223800; 2.西安建筑科技大学土木工程学院,西安 710055; 3.盐城市建筑设计研究院有限公司,盐城 224002; 4.融侨地产集团股份有限公司,南京 210000)
0 引 言
在近年来发生的大地震中,如1994年美国北岭地震、1999年台湾集集地震、2003年日本十胜冲地震、2008年汶川地震和2011年东日本大地震等,由于地震动中含有丰富的长周期分量,(超)高层结构、石油油罐、大跨桥梁等长周期结构出现了不同程度的破坏[1-3]。高层结构自振周期比较长,对长周期地震动比较敏感,其在长周期地震动作用下地震反应的问题引起了学者们的广泛关注。长周期地震动分为远场长周期地震动和近场长周期地震动。张振炫对比研究了远场长周期地震动和普通地震动作用下某50层钢筋混凝土框筒结构的弹性地震反应[4],Liao Wi比较分析了近场长周期地震动和普通地震动作用下某5层和12层钢筋混凝土框架结构的弹塑性地震反应[5],结果表明近、远场长周期地震动作用下高层结构的地震反应均大于普通地震动作用下的地震反应。然而,两类长周期地震动在峰值、频谱、持时、脉冲特性等方面存在较大的差异[6-7],对高层结构地震反应的影响规律也有所不同,目前缺乏两类长周期地震动作用下高层结构地震反应的对比研究。鉴于此,以某32层钢筋混凝土高层结构为背景工程,选取4条远场长周期地震动、4条近场长周期地震动作为输入,通过弹性时程分析法,探讨两类长周期地震动作用下高层结构的地震反应的差异。
1 工程概况与结构动力特性
某住宅小区9#楼,地下2层,地上32层,采用钢筋混凝土框架-剪力墙结构体系,首层层高5.4 m,2层层高3.8 m,3层(设备夹层)层高2.0 m,4~32层层高2.9 m,总高度95 m,结构平面尺寸为44 m×14.4 m,标准层平面布置图如图1所示。该工程的设计基准期为50年,安全等级为二级,抗震设防烈度为7度(0.1g),场地类别为Ⅲ类,设计地震分组为第二组,抗震设防分类为丙类。剪力墙厚度:基础顶至3层为200~400 mm,4~32层为200~250 mm,4层以下为剪力墙加强区;柱尺寸,400 mm×400 mm、500 mm×500 mm、500 mm×650 mm、500 mm×800 mm、550 mm×800 mm、600 mm×600 mm、600 mm×700 mm;梁尺寸:250 mm×400 mm、250 mm×450 mm、250 mm×500 mm;楼板厚度,120 mm。剪力墙、柱的混凝土强度等级:基础顶至11层C40,12~19层C35,20~32层C30;梁、板的混凝土强度等级:地下2~11层C35,12~32层C30;纵筋、箍筋,HRB400。
采用ABAQUS建立结构有限元分析模型。梁、柱采用铁木辛科梁单元B31,剪力墙、楼屋面板采用分层壳单元S4R;梁、柱纵筋采用rebar插入指定位置,剪力墙、楼屋面板分布钢筋采用rebar lay布置。所建模型如图2所示。对结构进行模态分析,提取前6阶振型,其中第1阶振型为横向水平振动,第2阶振型为纵向水平振动,第3阶振型为绕竖向的扭转振动。各阶振型的自振周期详见表1。结构的第一平动周期T1=3.48 s,第一扭转周期Tt=2.73 s,Tt/T1=0.78<0.9,满足规范要求,说明结构具有足够的抗扭刚度。
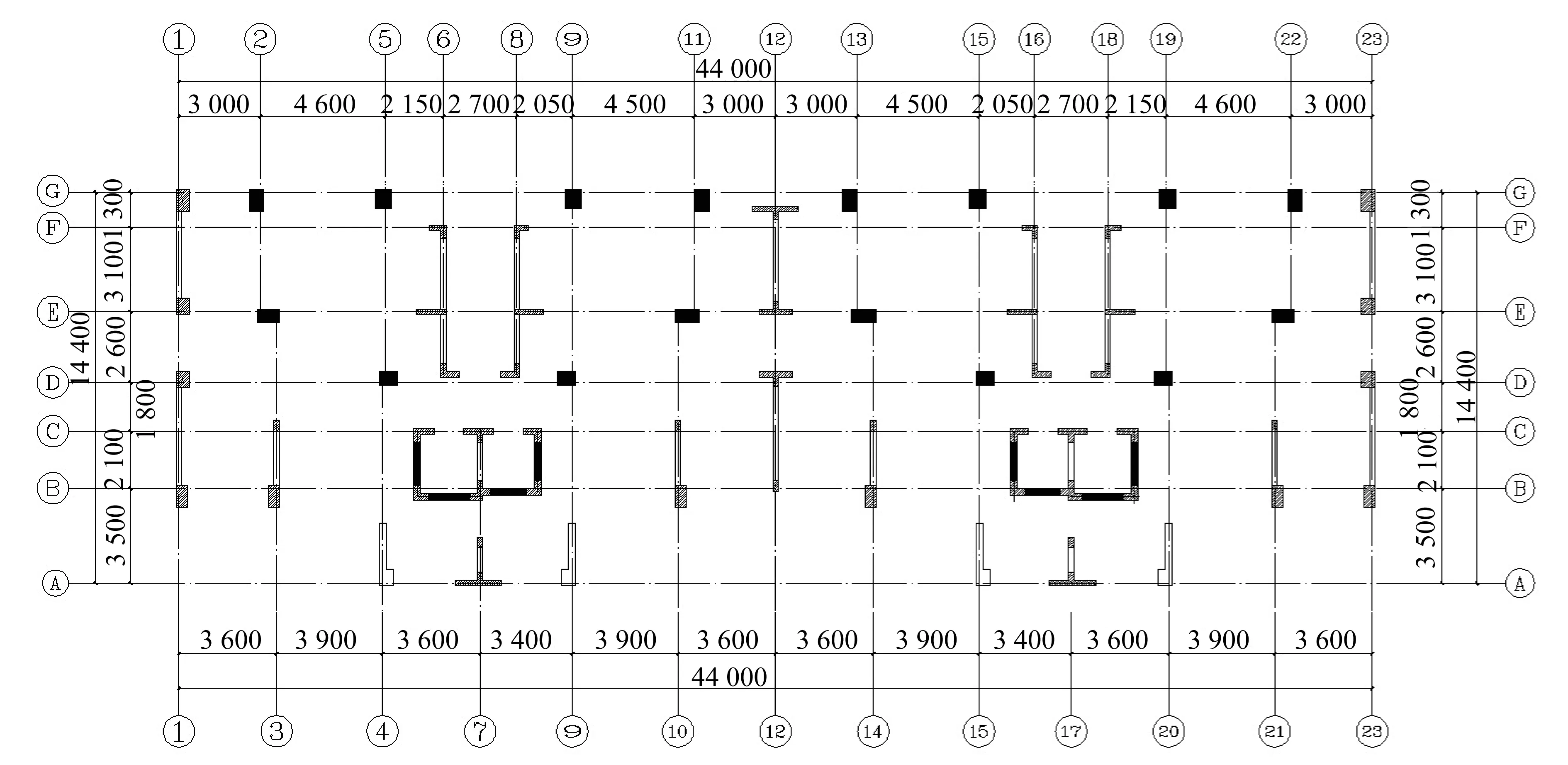
图1 结构标准层平面布置图(单位:mm)Fig.1 Plan view of standard floor (Unit:mm)

图2 结构有限元模型Fig.2 Finite element analysis model
表1结构前3阶自振周期

Table 1Period of first 3 modes vibration period of structure
2 地震动选取与能量特性分析
为分析两类长周期地震动作用下高层结构地震反应的差异,从1999年台湾集集地震记录中选取ILA004-EW、ILA004-NS、ILA056-NS和TCU115-NS作为典型远场长周期地震动,选取TCU052-EW、TCU052-NS、TCU068-NS和TCU094-NS作为典型近场长周期地震动,各条地震动的基本信息详见表2。限于篇幅,仅列出远场长周期地震动TCU115-NS和近场长周期地震动TCU052-NS的加速度时程曲线,分别见图3(a)和图3(b)。
地震动能量能够综合反映地震动的幅值、频谱、持时等特性。为了解各条地震动的能量特性,采用Hilbert-Huang变换的方法分别计算其Hilbert能量谱,其中远场长周期地震动TCU115-NS和近场长周期地震动TCU052-NS的Hilbert能量谱分别如图4(a)-(b)所示。可以看出,TCU115-NS的能量主要分布在0.2~0.5 Hz区段,TCU052-NS的能量主要分布在0.1~1.0 Hz区段,1.0 Hz以上区段几乎均无能量分布。由此可见,长周期地震动能量主要集中在较窄的低频段内。
表2各条长周期地震动的基本信息
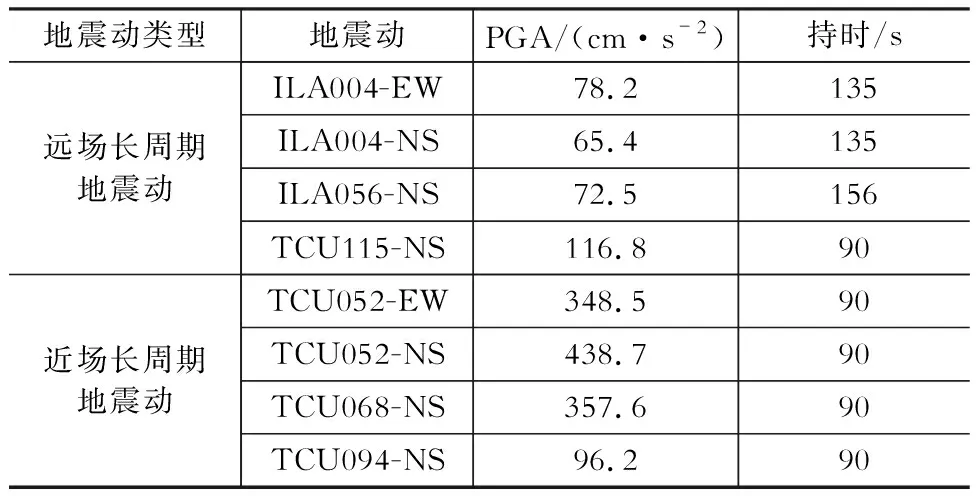
Table 2Basic information of long-period ground motions
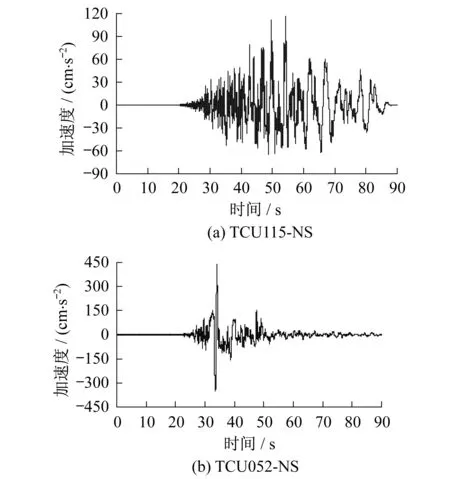
图3 典型长周期地震动的加速度时程曲线Fig.3 Acceleration time history curves of typical long-period ground motions
定义Hilbert能量平均周期TmE,按式(1)计算:
(1)
式中:fi为Hilbert能量离散频率,取0.1 Hz≤fi≤20 Hz;HEi为与fi对应的Hilbert能量。
相较于Fourier谱卓越周期,TmE能够反映地震动幅值、持时和主要频段对能量的影响,该值越大,地震动能量越集中在低频区段,长周期特性越显著。计算各条地震动的TmE,列于表3。从表3可以看出,各条地震动的TmE在3~5 s之间,长周期特性均非常明显;其中,远场长周期地震动ILA004-NS、近场长周期地震动TCU094-NS的TmE

图4 典型长周期地震动的Hilbert能量谱Fig.4 Hilbert energy spectrums of typical long-period ground motions
分别为3.72 s、3.25 s,与结构的基本周期3.48 s最为接近。
表3各条长周期地震动的平均周期TmE
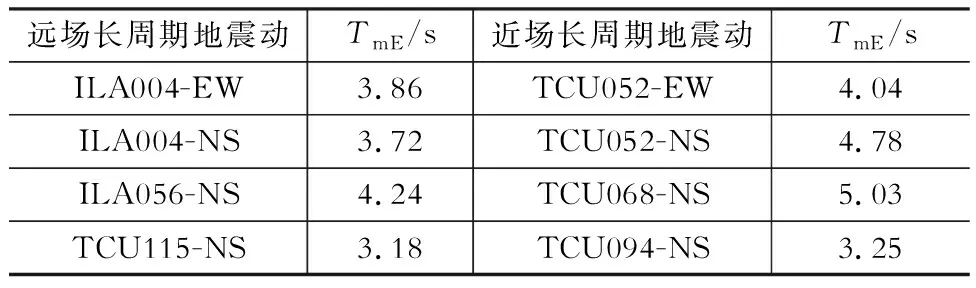
Table 3Average period TmE of long-period ground motions
3 长周期地震动作用下高层结构地震反应的对比分析
按照《建筑抗震设计规范》(GB 50011—2010)的规定,将各条长周期地震动的加速度峰值统一调整为35 cm/s,沿结构横向单向输入,进行该高层结构的弹性时程分析,计算其弹性地震反应,并提取各楼层的层间剪力、楼层位移和层间位移角等反应指标,比较其变化规律和差异。其中,结构的基底剪力、顶层位移、最大层间位移角和最大层间位移角所在楼层号的计算结果如表4所示。
表4长周期地震动作用下结构的弹性地震反应

Table 4Elastic seismic response of structure under long-period ground motions
3.1 层间剪力
远场、近场长周期地震动作用下结构的层间剪力分别如图5(a)和图5(b)所示,平均层间剪力如图5(c)所示。
分析图5(a)-(b)和表4可以看出,由于地震动的随机性,各条地震动的能量特性互不相同,各条地震动作用下结构的层间剪力也有所差异,但随着地震动的Hilbert能量平均周期TmE逐渐接近结构的基本周期,结构的层间剪力逐渐增大。例如,远场长周期地震动ILA056-NS、ILA004-EW、TCU115-EW、ILA004-NS的TmE与结构的基本周期3.48 s分别相差0.76 s、0.38 s、0.30 s和0.24 s,逐渐接近基本周期,计算结果表明,结构的层间剪力逐渐增大,以基底剪力为例,其值分别为11 345 kN、12 611 kN、13 263 kN和15 260 kN;近场长周期地震动TCU068-NS、TCU052-NS、TCU052-EW、TCU094-NS的TmE与结构的基本周期3.48 s分别相差1.55 s、1.30 s,0.56 s和0.23 s,逐渐接近基本周期,结果显示,除4层及以下,结构的层间剪力亦呈现逐渐增大的趋势。
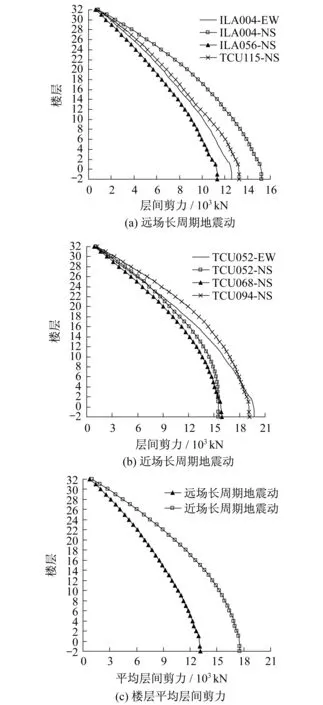
图5 长周期地震动作用下结构的层间剪力Fig.5 Inter-story shear forces of structure under long-period ground motions
综合比较图5(a)-(c)可以发现,近场长周期地震动作用下结构的层间剪力普遍大于远场长周期地震动作用。其中,近场长周期地震动TCU052-EW作用下结构的基底剪力最大,为19 714 kN,远场长周期地震动ILA056-NS作用下结构的基底剪力最小,为11 345 kN,前者是后者的1.74倍。近场长周期地震动作用下结构的平均基底剪力约为远场长周期地震动作用下的1.34倍。
3.2 楼层位移
远场、近场长周期地震动作用下结构的楼层位移分别如图6(a)和图6(b)所示,平均楼层位移如图6(c)所示。
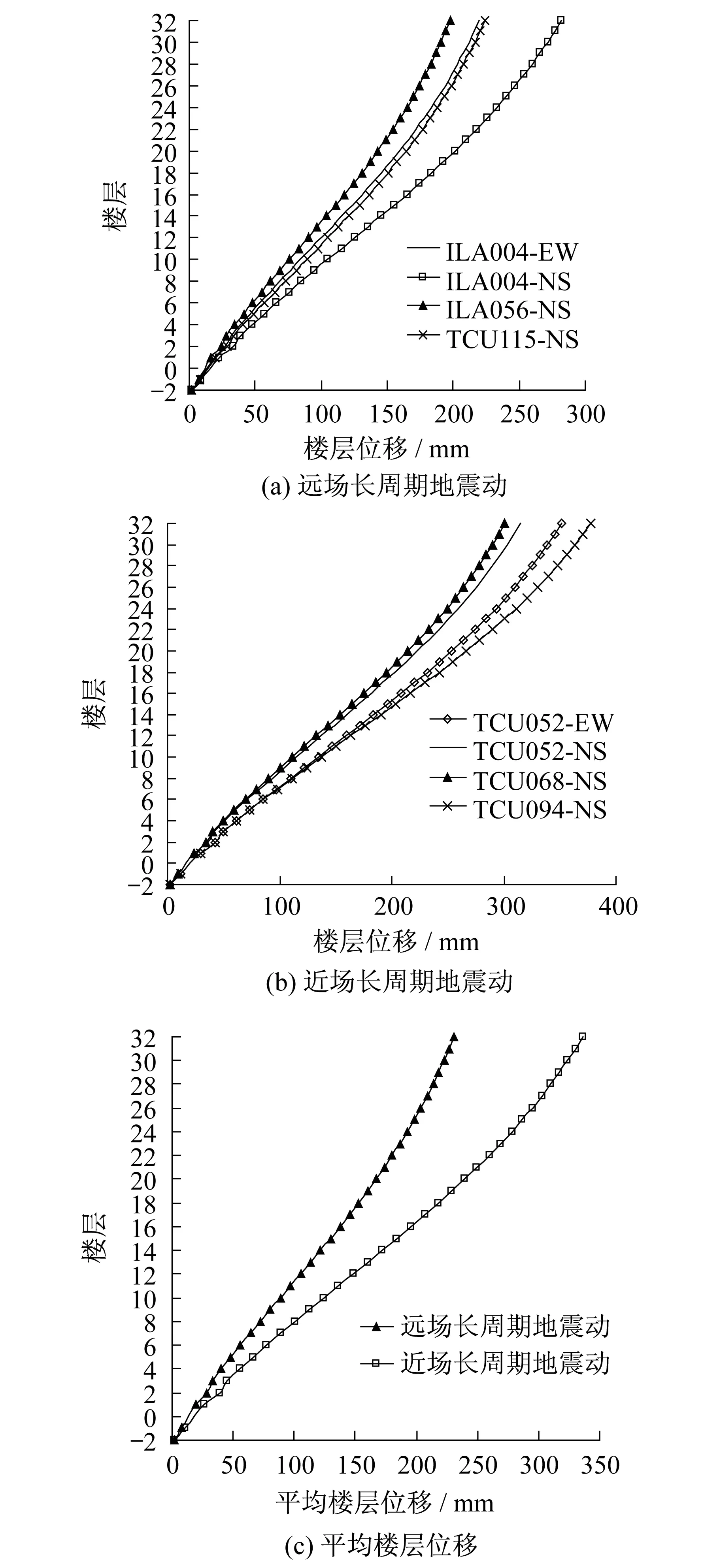
图6 长周期地震动作用下结构的楼层位移Fig.6 Floor displacement of structure under long-period ground motions
分析图6(a)-(c)和表4得出,两类长周期地震动作用下结构的楼层位移均随楼层的升高而逐渐增加,顶层位移最大;楼层位移曲线呈弯剪型。同时,楼层位移表现出与层间剪力相似的变化规律:
(1) 随着地震动的Hilbert能量平均周期TmE逐渐接近结构的基本周期,结构的楼层位移逐渐增大。以近场长周期地震动为例,TCU068-NS、TCU052-NS、TCU052-EW、TCU094-NS的TmE逐渐接近结构的基本周期,对应的结构顶层位移依次增加,分别为300.7 mm、315.22 mm、351.19 mm和377.44 mm,最大增加1.26倍。
(2) 近场长周期地震动作用下结构的楼层位移明显大于远场长周期地震动作用。虽然近场长周期地震动中TCU068-NS作用下结构的顶层位移最小,为300.7 mm,仍大于远场长周期地震动作用下最大的顶层位移282.12 mm,约为其1.07倍。近、远场长周期地震动作用下结构的顶层位移平均值相差1.45倍。
3.3 层间位移角
远场、近场长周期地震动作用下结构的层间位移角分别如图7(a)和图7(b)所示,平均层间位移角如图7(c)所示。
从图7(a)-(b)和表4可以看出,两类长周期地震动作用下结构的层间位移角的分布特点基本一致,从底层向上先逐渐增大,在中下部楼层达到最大后又逐渐减小,且最大层间位移角主要出现在12~15层。除地下2层外,各楼层的层间位移角均明显超出现行规范1/800的限值要求,远场、近场长周期地震动作用下结构的最大层间位移角甚至分别达到了1/285、1/213,超出了限值要求的2.81倍、3.76倍。
与结构的层间剪力、楼层位移的变化规律类似,随着地震动的Hilbert能量平均周期TmE逐渐接近结构的基本周期,结构的层间位移角亦逐渐增大。以远场长周期地震动为例,ILA056-NS、ILA004-EW、TCU115-EW、ILA004-NS的Tm逐渐接近结构的基本周期,对应的结构最大层间位移角依次增大,分别为1/403、1/362、1/348、1/285,最大增大1.41倍。
近场长周期地震动作用下结构的层间位移角普遍大于远场长周期地震动作用,由图7(c)易得,前者的最大层间位移角平均值约是后者的1.45倍。
4 结 论
在长周期地震动能量特性分析的基础上,探讨了两类长周期地震动作用下高层结构地震反应的变化规律和差异,得到如下结论:
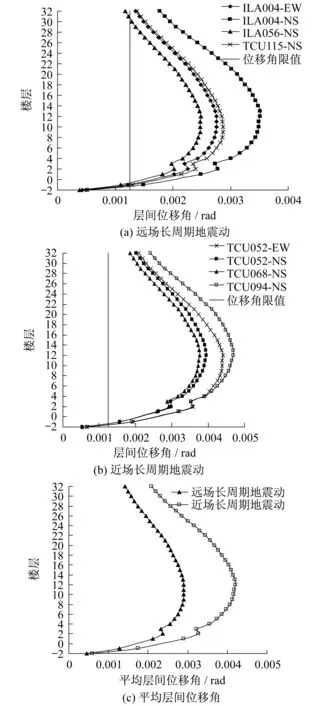
图7 长周期地震动作用下结构的层间位移角Fig.7 Inter-story displacement angle of structure under long-period ground motions
(1) 随着地震动的Hilbert能量平均周期TmE逐渐接近结构的基本周期,长周期地震动作用下结构的层间剪力、楼层位移和层间位移角呈现增大的趋势。
(2) 近场长周期地震动作用下结构的层间剪力、楼层位移和层间位移角普遍大于远场长周期地震动作用,前者的基底剪力、顶层位移、最大层间位移角的平均值分别约是后者的1.34倍、1.45倍、1.45倍。
(3) 两类长周期地震动作用下各楼层的层间位移角均明显超出现行规范1/800的限值要求,设计时应充分关注长周期地震动作用下高层结构的变形问题。

