高阻尼人-结构系统的共振频率研究

傅 豪 叶 茂 徐梅玲

(广州大学/广州大学-淡江大学工程灾害与控制联合研究中心,广州 511400 )

0 引 言

随着结构材料、工艺的不断更新,结构呈现出了跨度越来越大、整体越来越柔的特点,使得结构自振频率越来越低,人群的荷载作用致使结构更容易被诱发振动,此种现象在大跨度结构中尤为突出。2010年,山西藏山举行的某大型活动中,搭建的临时看台突然坍塌事件,导致数名人员受伤[1],孙昊[2]提出,在静止站立的单个人或人群会改变结构的动力学特性,所以人体自身对于结构有着重要的影响。因此,实际工程中考虑人体对结构的影响是必要的。目前,关于人体-结构相互作用的研究主要分为两方面:人体生物动力学和结构动力学[3]。在人体生物动力学中,Y.Matsumoto和Griffin[3]主要通过研究人体表观质量,分析人体静止站立的自然频率:其中,人体静止站立时水平方向的自振频率为0.5 Hz左右[4],竖直方向为5～6 Hz[5],并结合数学模型进行模拟[5]。在土木工程领域,早期研究人员将人体简化为附加质量作用于结构上,导致结构自振频率减小,阻尼不变,这与实际测结构不相符。直到1987年,Foschi和Gupta基于体系阻尼增加的现象,提出了人体应当被简化为一个有阻尼的动力模型[7]。再后来,Eills和Ji将人体简化为单自由度质量-弹簧-阻尼体系(SDOF)[8]和考虑质量器单自由度及两自由度质量-弹簧-阻尼体系[9-10]。E.Shahabpoor等[11]同样采用单自由度体系分体人体在结构上行走时对结构的影响。国内这方面的研究较少,杨予等[11]将人体站立竖直方向振动等效为单自由度模型进行参数研究,王海等[13]采用SDOF研究人体与梁相互作用的动力学模型以及其耦合作用时体系的响应。

已有的研究成果,有将人体简化为单自由度质量-弹簧体系,这种模型的缺点是无法解释人-结构相互作用体系的第二阶共振频率低于结构频率的特性[8]。同时,以往研究人员在探讨人-结构系统的动力特性时,采用系统的固有频率来代替共振频率进行讨论[13],这种简化对于低阻力的系统是能够接受的,但人体的高阻尼特性,使得这种简化在分析人-结构系统动力特性时存在一定的问题。基于以上讨论,本文将人体简化为两自由度质量-弹簧-阻尼系统[6],并结合Griffin[4]关于两自由度人体模型参数,提出了三自由度质量-弹簧-阻尼系统的人-结构系统模型,并以共振频率为研究对象,探讨人-结构系统的动力特性。

1 人-结构系统模型

高阻尼三自由度人-结构系统模型如图1所示,其中上面两自由度用于模拟人体。其中两自由度人体模型对应的模态质量为M1、M2,模态刚度为K1、K2,模态阻尼为C1、C2。该三自由度模型的最下面一个自由度用于模拟结构,MS、KS、CS分别为结构的模态质量、模态刚度、模态阻尼。采用x1、x2、xs分别表示三自由度M1、M2、MS的位移。F为对结构施加简谐荷载(Ps(t)=P0sinωt)的激振器,S为拾振器,用于采集结构在激振器作用下的加速度和位移,并计算共振频率。

2 人-结构系统共振频率

图1所示三自由度质量-弹簧-阻尼模型的运动方程下:

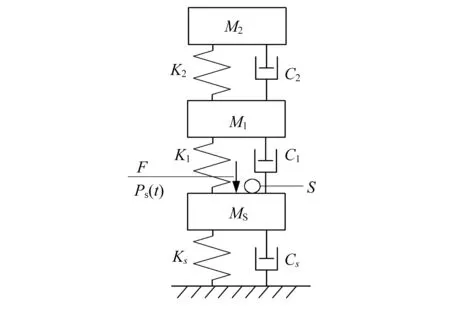
图1 人-结构体系模型Fig.1 Models of human-structure interaction

(1)

式中:

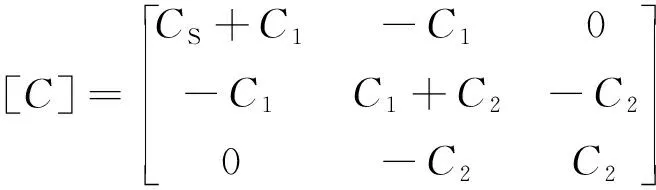
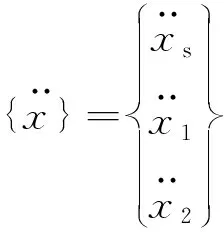
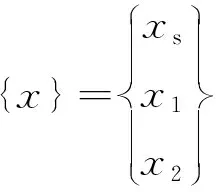
对式(1)进行傅里叶变换,变形得:

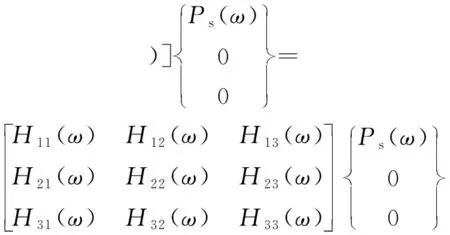
式中:

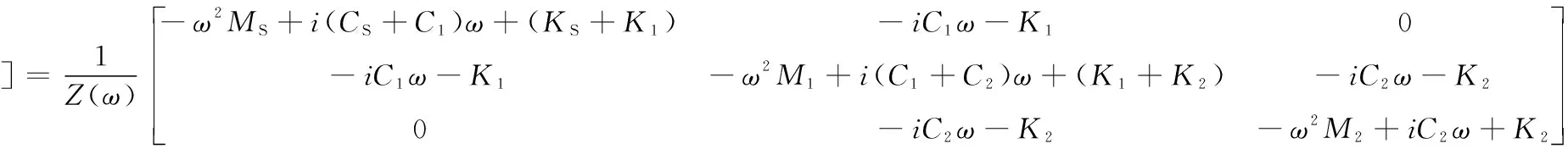
(2)

其中:

Z(ω)=[-MSω2+i(CS+C1)ω+(KS+K1)][-M2ω2+i(C2+C1)ω+(K2+K1)][-M2ω2+iC2ω+K2]-

(iC1ω+K1)2[-M2ω2+iC2ω+K2]-(iC2ω+K2)2[-MSω2+i(CS+C1)ω+(KS+K1)]

通过式(1)和式(2),可得结构加速的频率响应函数:

ω2H11(ω)=

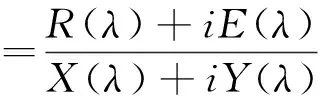
(3)

其中:

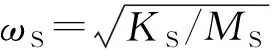
式(3)加速度频响函数的极大值点为系统的共振点,对该式求导,如下式所示:

(4)

要使式(3)的计算结果为系统的共振点,计算结果应满足式下式:

(5)

由式(4)知影响体系共振频率的因素有8个:α,α1,β1,β2,ξ1,ξ2,ξS和MS,其中MS为常数对方程(4)的根无影响,不影响体系的共振频率。在本文中,结构的阻尼比取ξS=0.01,于是主要影响体系响应共振频率的因子为6个,即:质量比α,α1,阻尼比ξ1,ξ2,频率比β1,β2(取β2=εβ1,故分析ε即可)。

3 人体模型参数

曼彻斯特大学JI教授团队[9]发表了关于竖直方向人-结构相互作用实验研究成果,测得单人(66.4 kg)站立于平台、4人(276.7 kg)站立于平台时结构响应的加速度如图3所示。其中该试验竖直固有频率为2.88 Hz,模态质量为180 kg,低阻尼体系。

根据人体生物学,Griffin等[6]关于人体竖直方向两自由度模型(图2)的参数,计算得到质量比为α=1.46,阻尼比为ξ1=0.37、ξ2=0.4,圆频率为ω1=87.34 rad/s、ω2=37.45 rad/s。于是,频率比β1=4.83、β2=2.07,质量比为α=1.46,JI的试验中,单人站立时有α1=0.21,4人时有α1=0.89。

将上述Griffin中人体模型参数,带入体系加速度频响函数式(3)中,并通过MATLAB绘制图形如图4所示。图中纵坐标为体系的加速度频响谱值A11(λ),横坐标为体系振动频率与结构固有频率的比值λ。将图4中模拟的结果与图3中进行对比得:单人站立平台时(图4(a)),试验中出现了一个比原结构频率低的共振频率,与试验的结果相符合(图3(a));4人站立于平台时,将模拟结果(图4(b))与实验结果(图3(b))对比知:图中出现了与试验结果相近的两个频率,这也与试验现象符合。但是,在图4(a)中,Griffin模型计算得到的结果在0～15 Hz范围内处还有出现一个共振值(5.429 Hz),但是Ji的实验中并没有识别这个结果,而图4(b)则展现出结果与实验结果非常相符,这应该与人-结构耦合程度(4人站立时,人-结构耦合更加明显)和测试分析技术的灵敏度有关。

上述与试验结果的对比分析表明,本文提出的高阻尼人-结构三自由度模型能较好地描述人-结构相互作用。为此,本文将以本模型为基础,对高阻尼人-结构三自由度模型进行系统分析,探讨人与结构间的质量比、频率比、阻尼比对人-结构体系共振频率的影响规律。

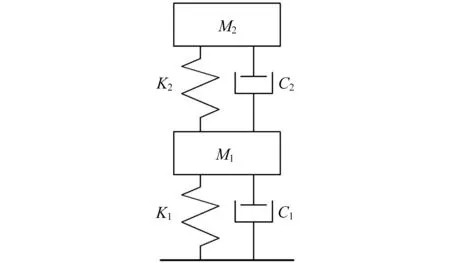
图2 两自由度人体模型模型(Griffin )Fig.2 TDOF of human body model (Griffin )

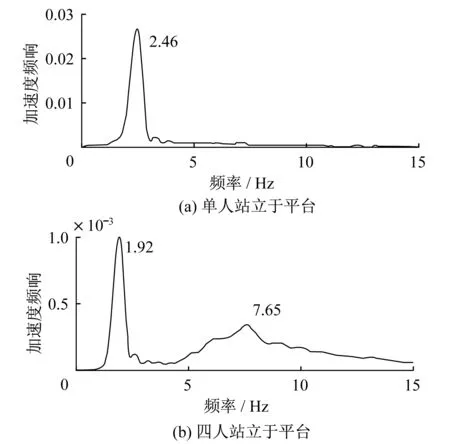
图3 加速度响应谱图(JI)Fig.3 Spectral response for acceleration (JI)

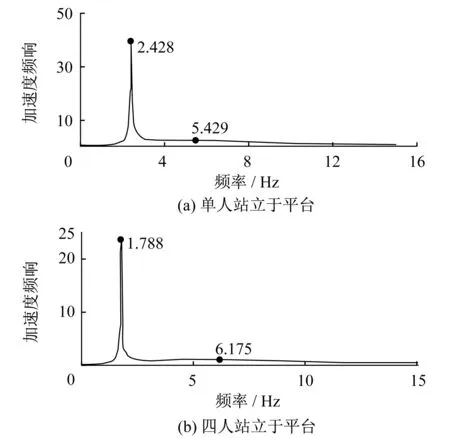
图4 模拟的加速度响应谱图(式(5))Fig.4 Spectral response for acceleration (Equation (5))

4 数值分析

将人-结构系统简化为三自由度质量-弹簧-阻尼模型,通过理论分析得到结构响应加速度频响函数解析式(4),可知影响体系共振频率主要因子有:两自由度人体模型模态质量比(α)、阻尼比(ξH1、ξH2),以及人与结构的模态质量比(α1、α2)、频率比(β1、β2)等。通过结合Griffin两自由度人体模型参数,分别对α1,β1,ξ1,ξ2进行定值数值分析。如秦敬伟等[15]展开单人一简支梁系统静态耦合下人梁质量比、频率比、阻尼比、人体位置等参数对系统竖向振动特性影响的理论研究中,分别独立的来研究对体系共振频率的影响,在研究其中一个参数,如频率比时,其他参数为定值,通过其数值分析导出的共振频率影响图来判断对结构整体共振频率的影响。则本文其结构模态质量比α1,频率比β1,阻尼比ξ1、ξ2四个参数,也是分别独立讨论,研究其对体系共振频率的影响。

结构的阻尼比取ξS=0.01,人体阻尼比为0.1～0.5[5,16]。

图5中为研究各个影响因子对体系共振频率的影响情况,纵轴为结构响应的加速度频率谱值,横轴为体系振动频率与结构基频的比值λ,表2为对应图中极大值对应的λ值。

图5(a)及表2(a)为人体与结构频率比β1对体系共振频率的影响情况;其中,β1分别取0.1、

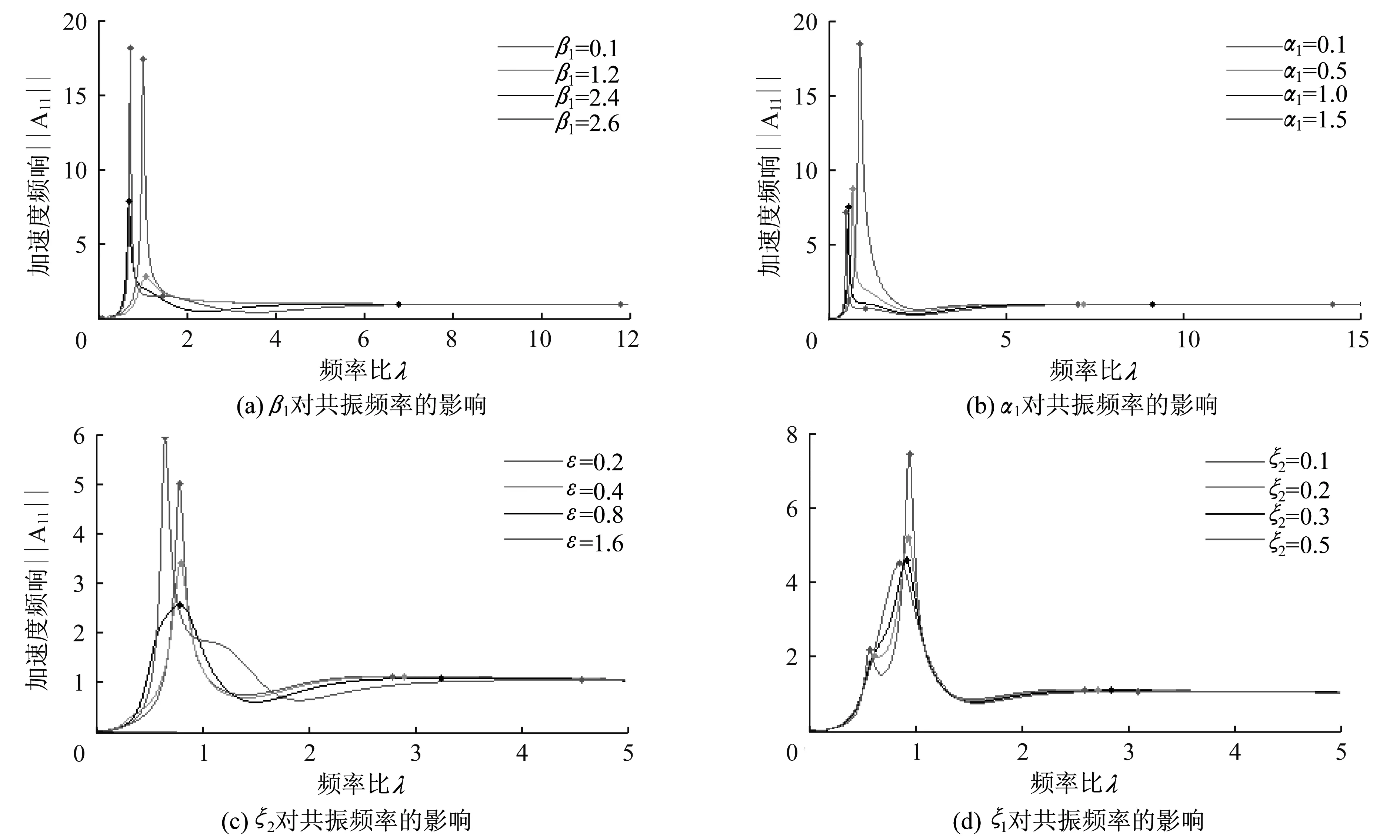
图5 各种参数对体系共振频率的影响图Fig.5 Effects of parameters on presence of resonance frequencies

表2各种参数对体系共振频率的影响

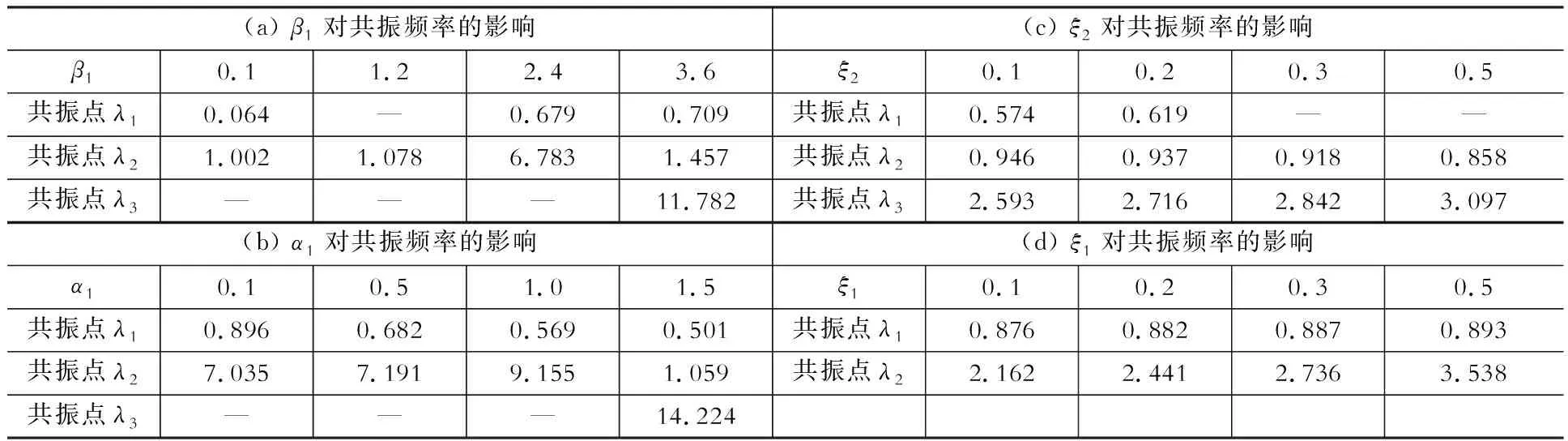
Table 2Effects of parameters on resonance frequencies

1.2、2.4、3.6,α=1.46,α1=0.25,ξ1=0.37,ξ2=0.4,ε=0.429。在此参数数取值情况下:随β1的增加,体系的共振频率成增大的趋势;同时,针对频率比β1,取(0,6)间隔为0.01的数值逐项计算知,当β1的取值在[3.47,6.00]内时,体系出现三个共振频率;取值在[0.44,0.87]内时,出现一个共振频率,其他情况均出现两个共振频率。

图5(b)及表2(b)为人体模型m1与结构模态质量比α1对体系共振频率的影响情况;α1取值为0.1、0.5、1.0、1.5,α=1.46,β1=2.5,ξ1=0.37,ξ2=0.4,ε=0.4。由于自由度m1占人体模型总质量的0.574倍,故人体模型总质量与结构的比值为α1/0.574。此参数数取值情况下:体系第一个共振频率随质量比α1的增加而成减小的趋势;同时,针对质量比α1,取(0,6)间隔为0.01的数值逐项计算知,当α1的取值在[1.41,1.90]内时(人体模型总质量与结构的比值取值为[2.46,3.31]),体系出现三个共振频率,其他情况均出现两个共振频率。

图5(c)及表2(c)和图5(d)及表2(d)分别表示人体阻尼比ξ1、ξ2对结构响应加速度响应情况的影响,其中α=1.46、α1=0.25、β1=1.5、ε=0.429:在ξ2=0.4时,阻尼比ξ1对体系第一阶共振频率的影响甚小;随着ξ1的增加,第二个共振频率呈增大的趋势;在ξ1=0.37时,随着ξ2的增加,第二个共振频率呈减小的趋势,且当ξ2取值较小时出现三个共振频率,且前两阶频率均小于原结构固有频率。同时,针对阻尼比ξ2,取(0,0.5)间隔为0.001的数值逐项计算知,当ξ2的取值在(0,0.208]内时,体系出现三个共振频率,其他情况均出现两个共振频率;同样范围内,分析ξ1的影响时,体系只出现两个共振频率。于是,可认为阻尼比ξ2对共振频率的影响比ξ1的影响更明显。

通过对每个影响因子,进行逐项数值分析可知:当采用Griffin的人体模型参数分析时,频率比β1对人-结构相互作用体系出现一个共振频率的影响,比质量比α1的影响更大;当质量比频率比取特定的值时,体系会出现一个、两个、三个共振频率。针对人-结构相互作用的三自由度模型分析。

5 结 论

(1) 本文针对人体的高阻尼特性,基于人体两自由度模型,提出了高阻尼人-结构相互作用系统的三自由度质量-弹簧-阻尼模型,推导得到结构响应的加速度频响谱的解析式。

(2) 通过模型与实验结果对比,Griffin人体模型参数能模拟出试验现象,能基本反映人-结构系统的动力特性。

(3) 在本文中,根据式(4)可知,主要影响体系响应共振频率的因子为:质量比α、α1,阻尼比ξ1、ξ2=,频率比β1、β2,本文通过结合Griffin两自由度人体模型参数,分别对质量比之一α1,频率比之一β1和ξ1、ξ2=进行定值数值分析。

(4)最后,对高阻尼人-结构三自由度模型进行了系统数值分析,分别独立的分析和研究了各个参数对体系共振频率的影响规律,表明:采用Griffin模型参数分析时,由于高阻尼的存在,只有当模态质量比α1、α2和频率比β1、β2取特定值时,才可能出现三个共振频率;同时,也解释了出现一个共振频率、两个共振频率以及前两阶频率均小于原结构固有频率的情况。在人-结构相互作用的的体系中,通过分析发现,若人-结构相互作用体系出现一个共振频率,频率比β1比质量比α1的影响更大;当质量比、频率比取特定的值时,体系会出现一个、两个或三个共振频率,阻尼比ξ2对共振频率的影响比ξ2的影响更明显。