四边简支CLT板的动力特性分析

王章进 周 叮 陆伟东

(南京工业大学土木工程学院,南京211816)

0 引 言

CLT[1]是由至少三层以上实木锯材或结构复合板材正交层合叠放,采用结构胶黏剂压制而成的一种新型木质工程材料,如图1所示。

对于CLT力学性能的研究,国外正在展开大量相关研究并取得了一系列成果。2010-2011年,R.Stürzenbecher和K.Hofstetter[1-2]基于Lekhnitskii[3]和Ren[4]板模型,提出了高效、相对精确的叠层板计算方法,并对3层以内的CLT板进行了受弯承载力对比分析。时境晶等[5]对重型木结构梁柱植筋节点进行了抗弯承载力研究,分析了其破坏形态和破坏机理,并提出了粘结应力和梁柱节点的抗弯承载力计算公式。CLT相比其他建筑材料,除了天然、可持续[6-7]的优点外,还具有良好的抗震性能,由CNR Ivalsa实施的SOFIE[8]项目和后续的关于CLT地震作用实验[9],展示了CLT在抗震方面的巨大潜力。Hirofumi Ido等[10]试验研究了宽度和层数对CLT简支梁弹性模量和抗拉强度的影响。熊海贝等[11]通过试验研究了不同支承形式和螺栓数目对梁柱式木框架体系的承载力和抗侧力影响。Bhaskar等[12]采用弹性力学精确方向研究了四边简支正交各向异性加筋板的动力性能。与轻型木结构相比,CLT结构还具有很好的绝热性能、隔声性能和耐火性能[13-14]。CLT技术在欧洲的住宅及非住宅的应用十分广泛,其中一些地区是地震多发区。梁、板是工程结构中最为常见的构件,当外部荷载的频率和构件的自振频率接近,容易引发共振而造成严重破坏,因此CLT作为一种木质新型板,对固有频率的精确求解是一个基本而有重要的问题。刘杏杏等[15]对胶合木框架-剪力墙结构抗侧力性能进行了通用有限元分析。杨正光等[16]利用状态空间法并结合级数展开法求解了四边简支功能梯度矩形板的静力弯曲和自由振动问题。范家让[17]基于三维弹性理论,运用状态空间法,推导得到多种边界条件下的层合板、壳(指单层板壳按一定顺序和角度叠层起来)静力弯曲解和自由振动的解析解。根据人体对振动的敏感度,欧洲规范5和英联邦设计标准要求无活载楼板的固有频率不宜低于8 Hz,Jan Weckendorf和Ian Smith等[18-19]对木结构楼板的振动舒适度进了较为系统的分析,分别对不同类型的CLT板、不同支承和边界条件、施工细节以及人体对楼板的模态、频率及阻尼的影响。Jarnero K等[20]分别从施工现场和实验室测试木结构楼板振动特性进行了分析,发现现场测试的楼板阻尼比远高于实验室测试的楼板阻尼比。

本文将CLT板作为中厚板,采用弹性力学[21]的精确方法对CLT板的动力学[22]特性进行分析,首先确定整体坐标系下刚度系数与工程弹性系数的关系,然后由CLT板上下表面的界面条件,建立CLT板的状态传递方程,由初始位移不全为零,给出任意厚度CLT板的各阶固有频率的解法。

1 CLT板刚度系数与工程常数的关系

如图2所示为四边简支CLT的模型图,长度为a,宽度为b,密度为ρ,CLT板的厚度为h。以第一层板x轴为顺纹方向,y轴为横纹方向。第二层板则刚好相反,x轴为横纹方向,y轴为顺纹方向。每个相邻层依次交替正交铺设。共有p层,下标j表示第j层而言。

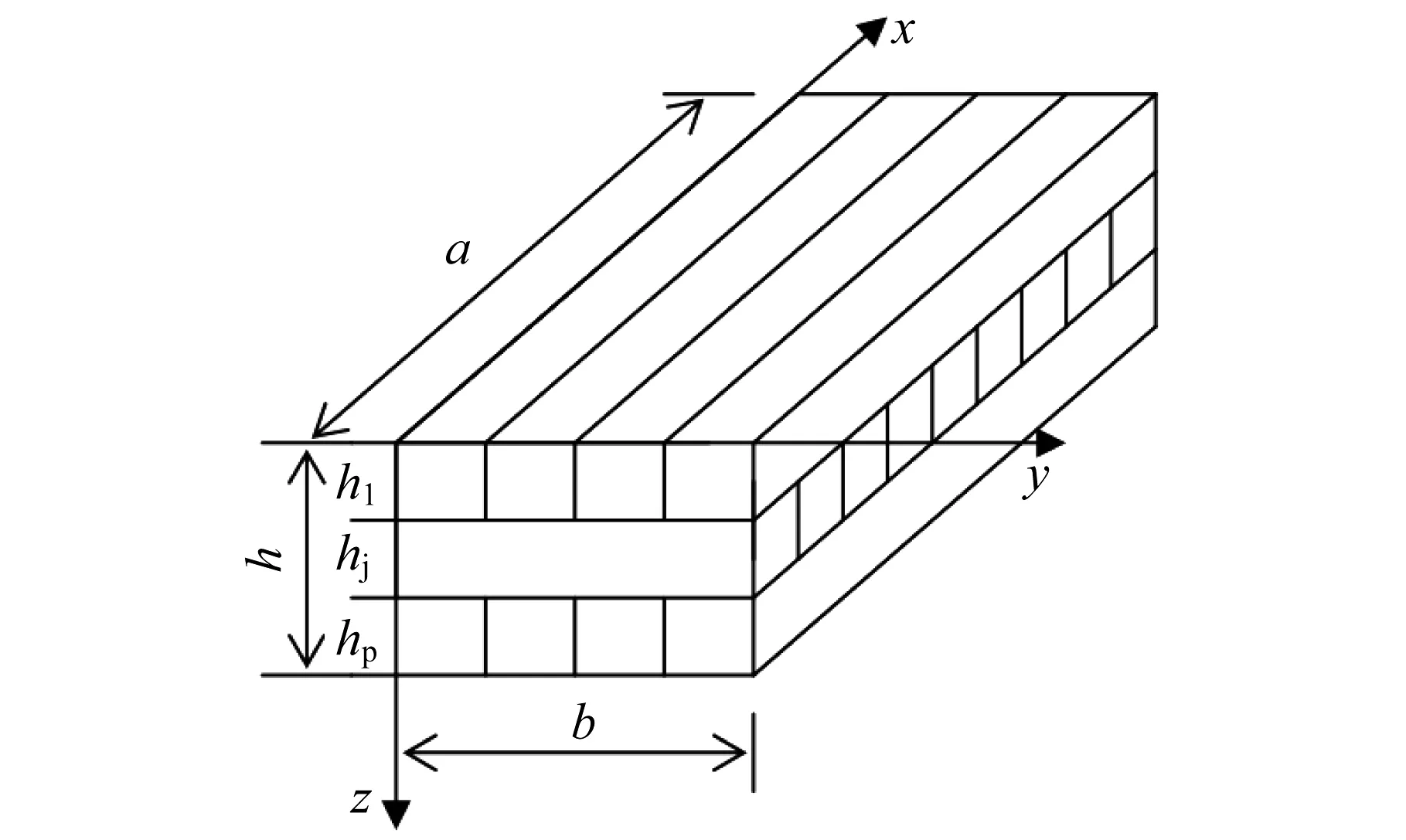
图2 CLT模型图Fig.2 Model of CLT

用E1,E2,E3分别表示木材在x、y、z方向的弹性模量。μ12表示x方向拉伸(压缩)引起y方向的缩短(伸长)的泊松比,其余类推。μ21表示y方向拉伸(压缩)引起x方向的缩短(伸长)的泊松比其余类推。G23表示y和z方向之间直角变化的剪切模量,其余类推。由广义胡可定律可知,对于正交异性体,刚度系数Cij=Cji(i,j=1,2,…,6),由应力-应变关系可得:

(1)

用工程弹性常数表示,由叠加原理可得

(2)

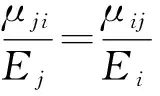
E1μ21=E2μ12,E2μ32=E3μ23,E3μ12=E1μ31

(3)

将式(3)代入式(2)进行求逆,与式(1)联立可求得:

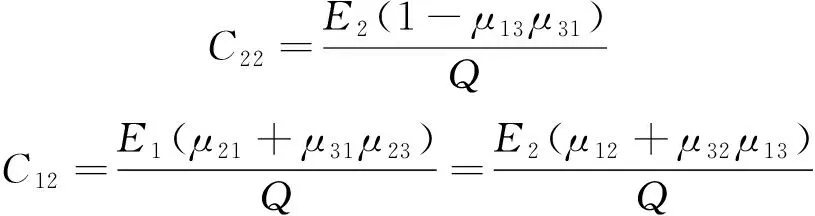
Q=1-μ12μ21-μ23μ32-μ31μ13-2μ12μ23μ31

(4)

以上公式可直接应用于木材沿x轴为顺纹的情况,对于正交铺设的木板,若y轴为顺纹方向,只需将式(4)中的工程常数E、μ、G的下标1与2进行互换,便可得到y轴为顺纹方向情况下的刚度系数。故只要知道这9个工程弹性常数即可得到任意一层板在整体坐标系下的刚度系数矩阵。

1.1 基本方程及单层板自由振动方程的解

如图3所示为单层的四边简支CLT板模型,长度为a,宽度为b,板厚度为h,密度为ρ。在直角坐标系中,x轴和y轴分别为木材的顺纹方向和横纹方向。

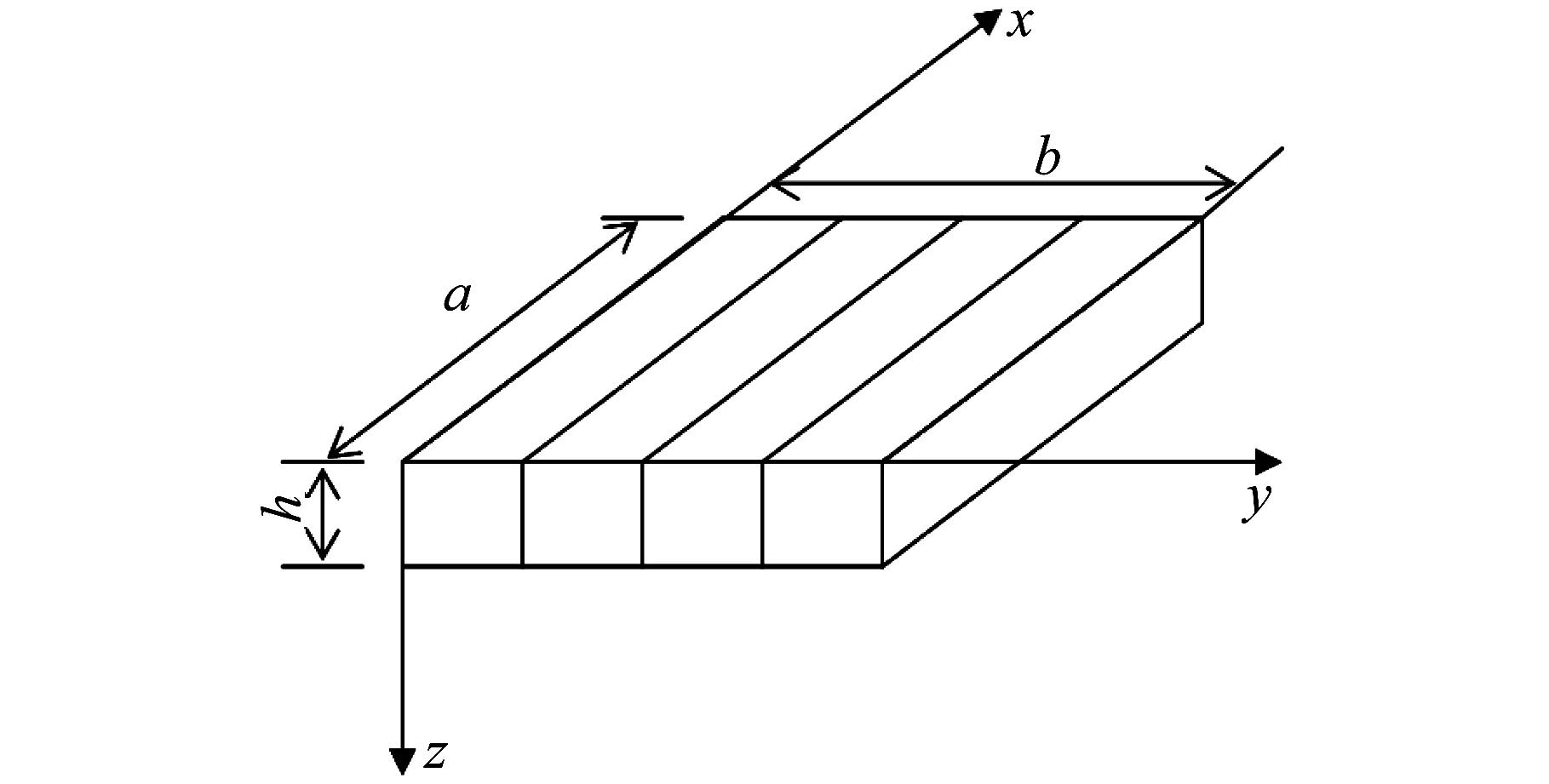
图3 单层CLT板模型Fig.3 Model of single-layer CLT plate

木材为正交异性弹性体,本构方程为:

(5)

αU+C5βV

(6)

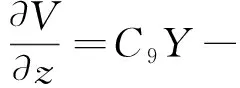
(7)

(8)

由应力位移表示的动力方程可知:

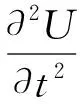
(9)

(10)

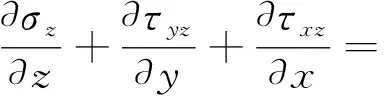
(11)

由式(11)可得:

ξ2U-αX-βY

(12)

由式(5)可得σx,σy,τxy:

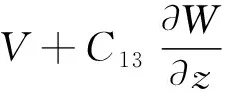
(13)

(14)

τxy=C6(αV+βU)

(15)

将式(13)和式(15)代入式(9),并用式(6)式简化可得:

(16)

将式(14)和式(15)代入式(10),并用式(6)进行简化得:

(17)

将式(6)至式(17)的6个方程写成矩阵形式,则有:

(18)

令

则式(18)转化为

(19)

将式(6)分别代入式(13)、式(14)和式(15)并化简得:

(20)

令

(21)

上式满足四边简支的边界条件:

x=0,a;σx=0,W=0,V=0,

y=0,b;σy=0,W=0,U=0

(22)

将式(21)代入式(19),对于每对m-n都有:

(23)

上式中,

(24)

由状态方程的解可知：

(25)

令

(26)

D(z,ω)=eD·z

(27)

则式(25)变为：

R(z)=D(z,ω)·R(0),z∈[0,h]

(28)

当z=h时,有R(h)=D(h,ω)R(0),R(0)为初始值,即CLT板上表面(z=0)处的3个位移分量和3个应力分量。矩阵的指数函数eD.z,有多种解析解法,这里采用凯莱哈密顿(Cayley-Hamilton)定理进行求解。

1.2 边界条件及固有频率的解

由已知条件可知CLT板在自由振动时,上、下表面外力:

上表面:Zmn(0)=0,Xmn(0)=0,Ymn(0)=0,

下表面:Zmn(h)=0,Xmn(h)=0,Ymn(h)=0,

(29)

将上式代入式(28),可得：

(30)

由上式可得：

(31)

令

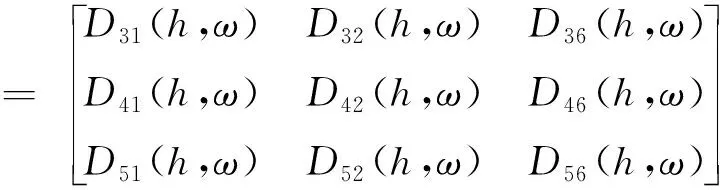
(32)

则式(31)转化为：

(33)

由于Umn(0),Vmn(0),Wmn(0)不全为零,故：

D*(h,ω)=0

(34)

上式即为单层正交异性板的频率方程,它是一个超越方程,该方程对于每一对m-n,都有无数个解,对应于无穷个固有频率,当m、n的值确定时,由MATLAB内置的搜根程序对式(34)的零点进行求解,可得到最小的非零实根,即为模态(m,n)的固有频率。

2 四边简支CLT板的自由振动求解

多层正交铺设CLT板模型如图2所示,重复单层CLT板自由振动方程推导过程可得：

Rj(z)=Dj(z,ω)·Rj(0),z∈[0,hj],

(35)

式(35)中,

(36)

(37)

在式(35)中,令z=hj得：

Rj(hj)=Dj(hj,ω)·Rj(0)

(38)

Dj(hj,w)为6阶常元素矩阵且因层而异。当j=1,2时,分别有：

R1(h1)=D1(h1,ω)·R1(0)

(39)

R2(h2)=D2(h2,ω)·R2(0)

(40)

R1(h1)为第一层下表面6个应力及位移量,R2(0)为第二层上表面6个应力及位移量。根据层间应力和位移的连续条件,该两组量相等,即：

R1(h1)=R2(0)

则由式(39)和式(40)得:

R2(h2)=D2(h2,ω)·D1(h1,ω)·R1(0)

(41)

逐层类推,可得:

Rp(hp)=Dp(hp,ω)·Dp-1(hp-1,ω)…

D2(h2,ω)·D1(h1,ω)·R1(0)

(42)

Rp(hp)=∏(hp,ω)·R1(0)

(43)

R1(0)为初始值,∏为6阶常元素矩阵,式(43)的显式为：

(44)

式(44)经过简单运算可得:

(45)

2.1 边界条件及固有频率的解

由已知条件可知CLT板自由振动时,上、下表面外力:

第1层上表面:

Zmn(0)=0,Xmn(0)=0,Ymn(0)=0,

第p层下表面:

Zmn(hp)=0,Xmn(hp)=0,Ymn(hp)=0

(46)

将式(46)代入式(45),可得：

(47)

令

(48)

由于Umn(0),Vmn(0),Wmn(0)不全为零,故有:

∏*(hp,ω)=0

(49)

式(49)即为四边简支CLT板的固有频率方程,这也是一个超越方程,求解方式与式(34)相同,由MATLAB进行求解,得到对应模态下的固有频率。

3 参数分析

CLT主要由杉木或松木制作而成,参考文献[23]给出的木材的材性参数,取花旗松的9个工程常数分别为:E1=10 800,E2=734,E3=540,G12=690,G13=843,G23=76(单位:MPa),泊松比μ12=0.292,μ13=0.449,μ23=0.390。四边简支CLT板的长度a=3 000 mm,宽度b=3 000 mm,密度ρ=0.49 g/cm3,板的总厚度h=200 mm,层数为p,每层等厚(h1=h2=…=hp=d),CLT板的第一层以顺纹方向为x轴方向。

下面分析四边简支CLT板的动力学特性,并与有限元软件Abaqus的结果进行比较。Abaqus分析四边简支CLT板采用三维实体建模,使用C3D8R单元,层间接触面采用tie绑定约束,对x=0,a和y=0,b界面采取反对称约束模拟四边简支边界条件,表1给出了p=3时,总厚度h=200 mm四边简支CLT板的前5阶固有频率,由表1可以看出,本文解与有限元解吻合得很好,前五阶频率中最大误差仅为2.0%,验证了本文解的正确性。

表1本文解与有限元解的比较

Table 1Comparison of present solutions with FE solutions

图4 四边简支CLT板自由振动第一阶模态Fig.4 Fundamental mode shape of simply supported CLT plate

图5 四边简支CLT板自由振动第二阶模态Fig.5 Second mode shape of simply supported CLT plate

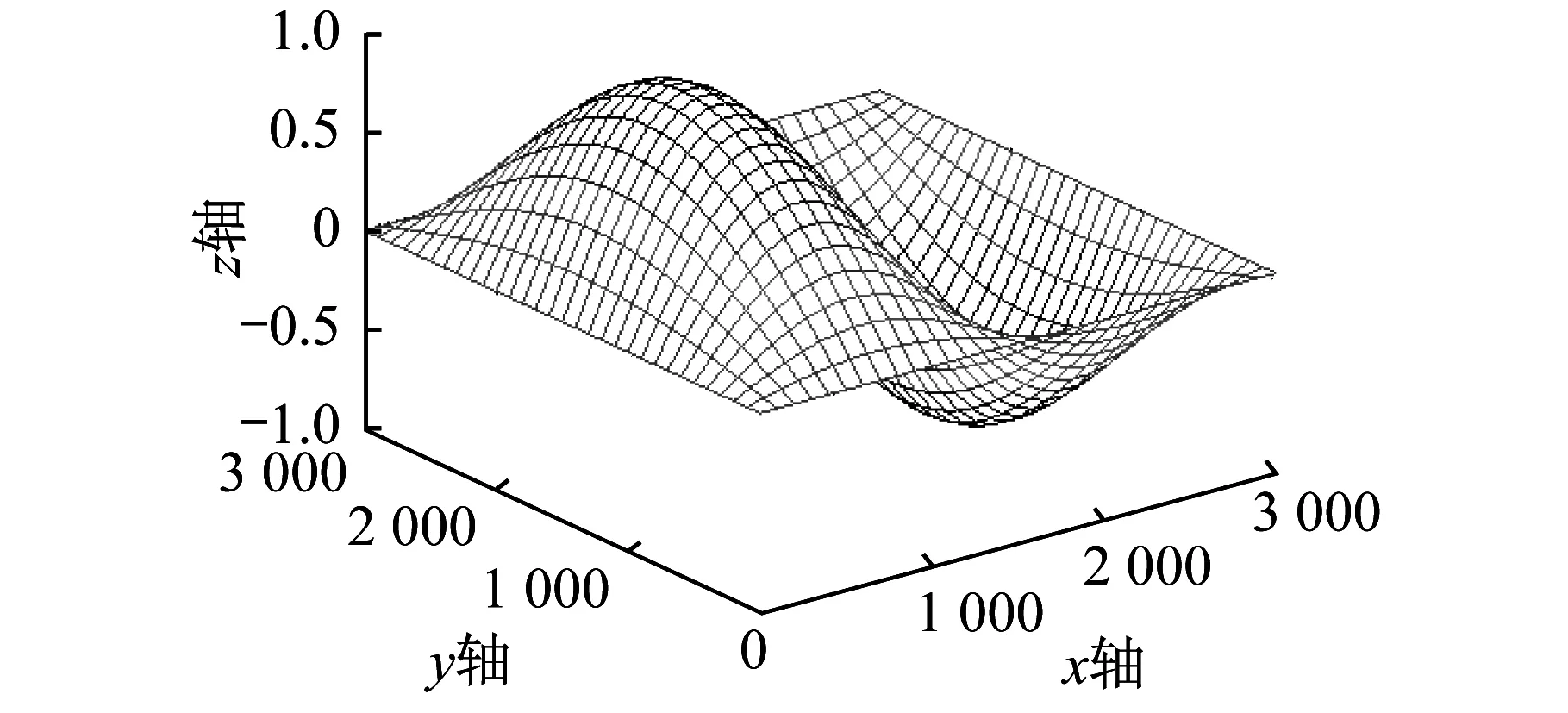
图6 四边简支CLT板自由振动第三阶模态Fig.6 Third mode shape of simply supported CLT plate

3.1 层数对四边简支CLT板固有频率的影响

CLT板的材料性质和模型尺寸如前所述,保持总厚度h=200 mm不变,取层数p=3,5,7时,研究不同层数四边简支CLT板的无阻尼自由动力特性。图7给出了不同层数对四边简支CLT板前5阶固有频率的影响。

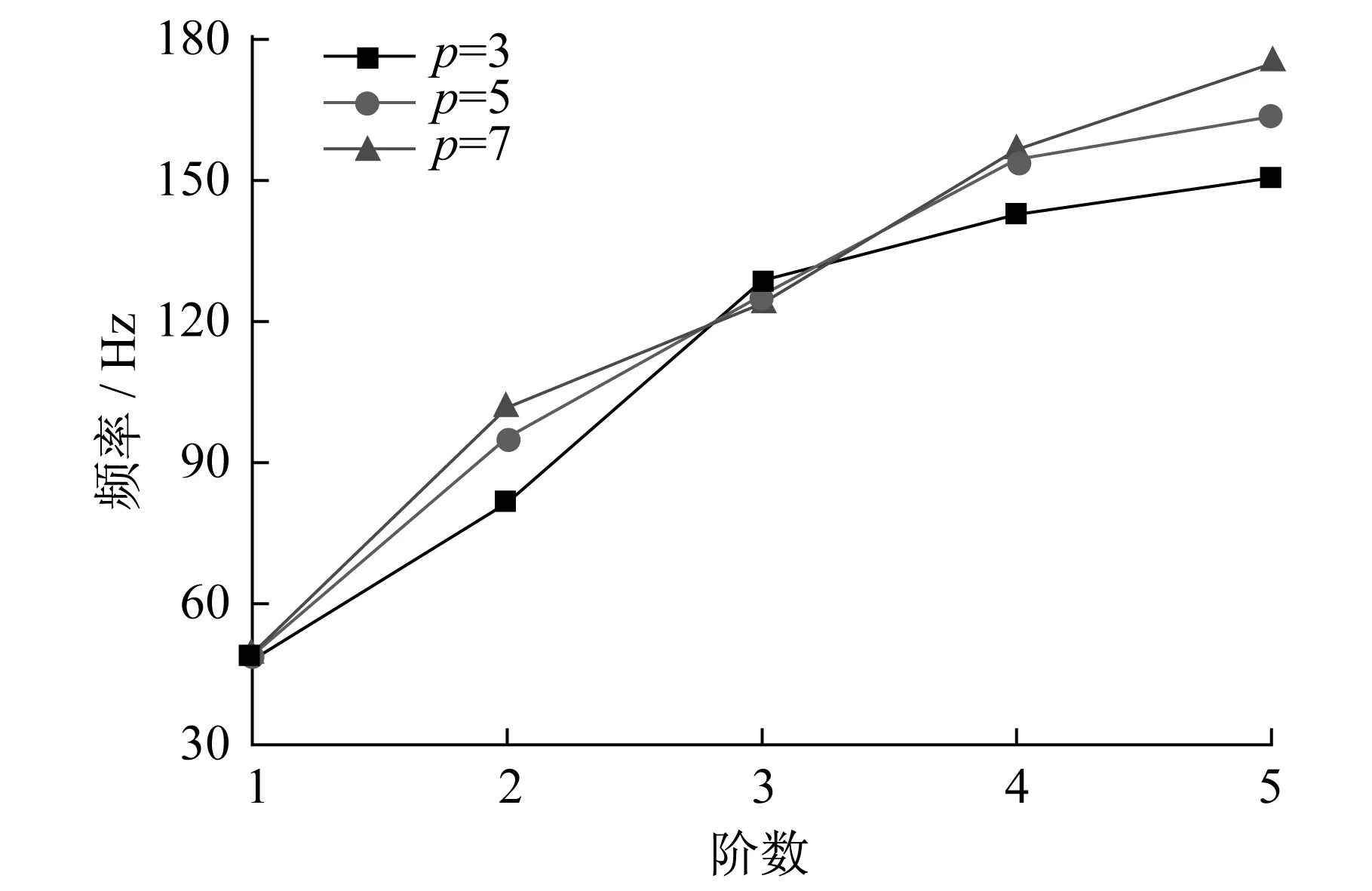
图7 不同层数对四边简支CLT板固有频率的影响Fig.7 Effect of different number of layers on vibration frequencies of simply supported CLT plates

从图7可以看出,四边简支CLT板除三阶固有频率外,其余各阶频率随着层数的增加而增大,四边简支CLT板的刚度随着层数的增加刚度增大。三阶固有频率对应的模态(m=2,n=1),如图6所示。由于CLT板采用正交铺设,在厚度保持不变的情况下,随着层数的增大,其x轴方向的刚度逐渐减小,而y轴方向的刚度则逐渐增大,所以对于第三阶模态,CLT板的三阶固有频率随着层数的增大而减小,符合工程实际情况。但是层数的变化对四边简支CLT板的自由振动频率影响不是很明显,层数p从3层到7层时,一阶频率只提高了2.9%。

3.2 宽厚比对四边简支CLT板固有频率的影响

四边简支CLT板的材料性质、模型的长和宽如前所述,保持CLT边长a不变,取层数p=3,改变总厚度h,研究具有不同宽厚比(h/a) 四边简支CLT板的无阻尼自由动力特性。表2给出了不同宽厚比对四边简支CLT板前5阶固有频率的影响。

由表2可以看出,四边简支CLT板的各阶固有频率均随着宽厚比(h/a)的增大而增大,即刚度随着宽厚比的增大而增大。宽厚比的变化对四边简支CLT板的固有频率影响较大,但各阶固有频率的增长率随着宽厚比的增大有所降低,如宽厚比(h/a)分别从0.05～0.1和0.1～0.2时,一阶固有频率增长率分别为67.3%和44.7%,固有频率增长率有所降低。

表2不同宽厚比(h/a)对四边简支
CLT板固有频率的影响

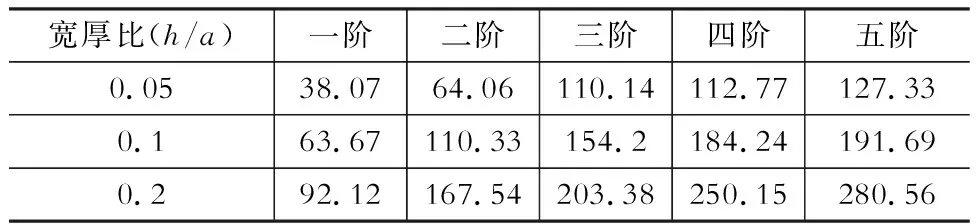
Table 2Effect of h/a-ratio on vibration frequencies of simply supported CLT plates

3.3 长宽比对四边简支CLT板固有频率的影响

四边简支CLT板的材料性质如前所述,保持CLT边宽b=3 000 mm,厚度h=200 mm不变,取层数p=3,改变边长a,研究具有不同长宽比(a/b) 四边简支CLT板的无阻尼自由动力特性。表3给出了不同长宽比对四边简支CLT板前5阶固有频率的影响。

表3不同长宽比(a/b)对四边简支
CLT板固有频率的影响

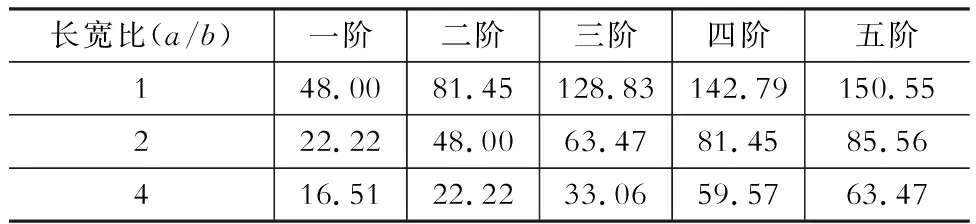
Table 3Effect of a/b-ratio on vibration frequenciesof simply supported CLT plates

从表3可以看出,四边简支CLT板的各阶固有频率均随着长宽比的增大而降低,即刚度随着长宽比的增大而减小。长宽比的变化对四边简支CLT板的固有频率也具有较大影响,但各阶固有频率的增长率随着长宽比的增大而有所降低,如长宽比分别从1～2和2～4时,一阶固有频率增长率分别-53.7%和-25.7%,固有频率增长率也有所降低。

4 结 论

本文对四边简支CLT板的动力特性进行了分析,分别研究了层数、宽厚比和长宽比对四边简支CLT板的自由振动特性影响。将CLT板视为正交各向异性材料,从三维弹性基本理论出发,不作任何假设,通过建立状态方程,导出四边简支CLT板的频率方程,由初始位移Umn(0),Vmn(0),Wmn(0)不全为零,从而得到以固有角频率为未知量的行列式为零,数值搜根求得各阶固有频率。数值结果与有限元软件Abaqus进行比较,显示出了很好的一致性。

(1) 研究结果显示四边简支CLT板的层数、宽厚比和长宽比对四边简支CLT板的各阶固有频率均有影响。宽厚比越大,长宽比越小,四边简支CLT板的各阶固有频率均相应增大;四边简支CLT板的各阶固有频率(除三阶频率外)随层数的增多而增大。

(2) 通过对比可知,宽厚比和长宽比对四边简支CLT板的固有频率影响远大层数对四边简支CLT板的固有频率影响,研究可以为四边简支CLT板作为楼板、墙体等结构构件的自由振动固有频率精确解的求解提供了计算方法,并对如何改善CLT板固有频率提供了指导。