单箱单室薄壁箱梁约束扭转分析

郭靖宇，管松，年玉泽，万水

(1.阜阳市公路管理局，安徽 阜阳 236000； 2.东南大学交通学院，江苏 南京 210096)

薄壁箱梁截面由于抗弯抗扭刚度大、截面整体性能好和施工适应性强等优点，广泛应用于桥梁结构[1-2]。目前桥梁设计主要采用平面杆系矩阵位移法[3]，该方法通过每个单元设有2个节点，每个节点6个自由度来分析宏观弯矩、剪力、扭矩沿梁轴向的分布规律。弯矩、剪力与正应力、剪应力已建立了比较完善的函数式[4]；而偏心荷载作用下扭矩与正应力、剪应力则难以建立对应关系，这就给目前的箱形梁桥设计造成了困难，无法从力学角度解释扭矩与应力之间的关系。

本文从静力学平衡方程、几何方程、物理方程出发，利用位移法建立微元体之间的微分方程，考虑边界条件的初始条件求解微分方程，得到扭矩与应力之间的数值函数关系。选取某单箱单室混凝土简支箱梁桥进行算例分析，进一步了解扭转作用下的翘曲正应力和约束扭转剪应力的分布规律。

1 纵向位移假定

对箱形梁约束扭转的求解思路是位移法求解，先要构造位移函数表达式，由于箱形梁的复杂性，无法直接根据边界条件得出位移函数表达式。我们从自由扭转的翘曲位移模式出发，通过类比研究，对约束扭转的翘曲位移模式进行假定。

如图1，根据微元体几何方程[5]16，可得自由扭转下的翘曲位移模式。

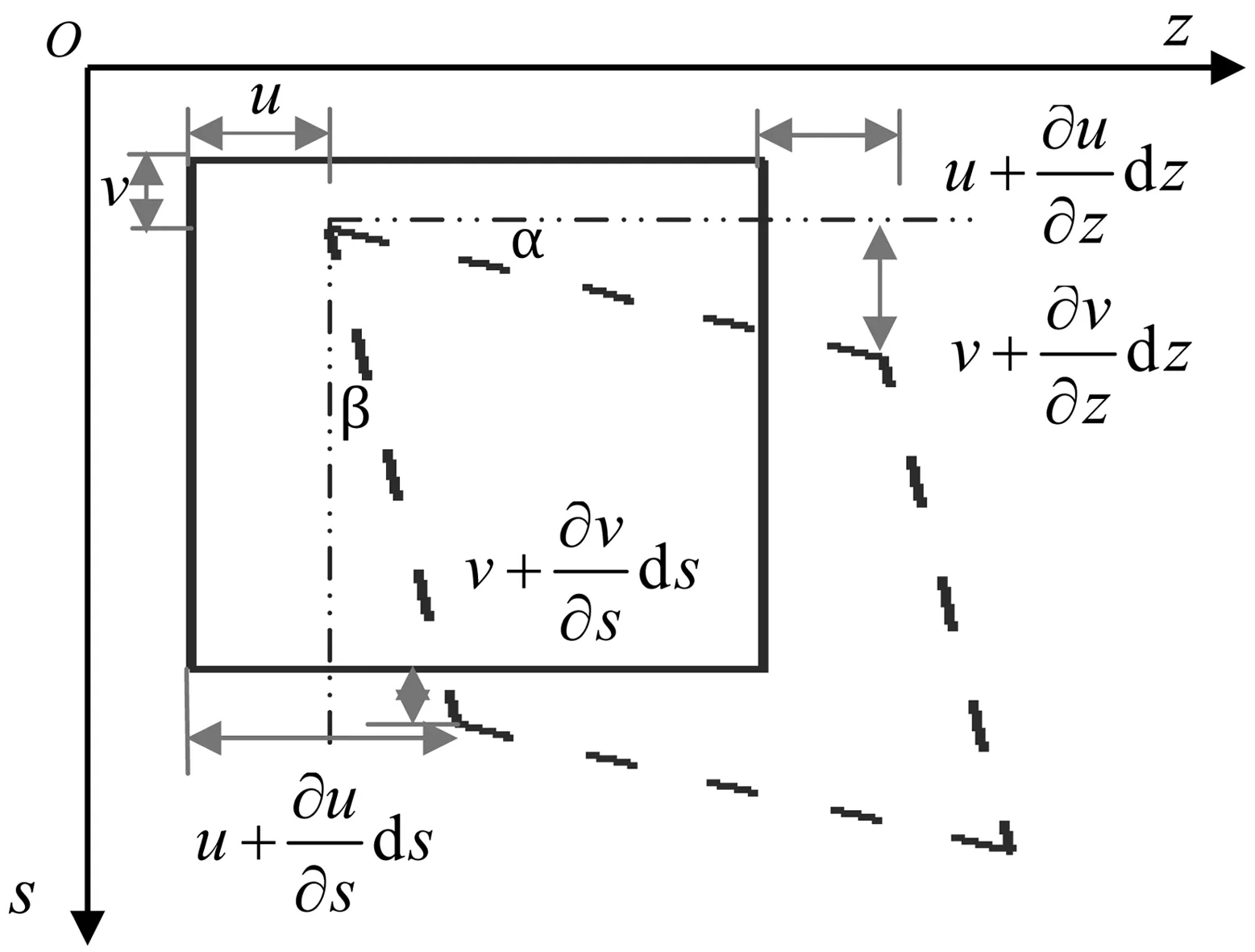
图1 箱形梁微元形变示意图

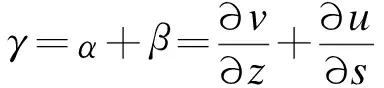
(1)

v=hθ(z)

(2)

式中，h为截面中心轴到箱壁中心的距离。将式(2)代入式(1)，可得

(3)

(4)

对式(4)沿箱梁路径积分一周，

∮γds=∮hθ′(z)ds

(5)

(6)

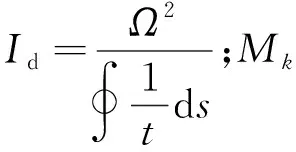
式(4)可表示为

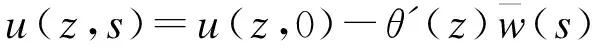
(7)

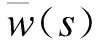
由于刚性扭转时截面纵向变形受到约束，式(7)中θ′(z)为常数项，与z轴无关，无法反映结构真实的翘曲情况。乌曼斯基(A.A.YManCKttfi)提出，约束扭转的翘曲变形函数与自由扭转翘曲变形函数相似，反映翘曲程度的函数为β′(z)，不等于θ′(z)，β′(z)为关于z的函数[6]。式(7)可表示为

(8)

2 扭转中心位置

选取图2所示截面的形心A作为极点，以竖向对称轴与箱形梁边的交接点C作为主扇形零点，实际扭转中心B满足式(9)的条件。

(9)

图2 A、B为极点的2个扇形坐标关系

h=[(x-xA)-(y-yA)cotα]sinα

(10)

dwA=hds

(11)

(12)

同理，以截面形心B为极点，可得到类似结论。

(13)

(14)

对式(14)积分，

(15)

将式(15)代入扭转中心条件公式(9)，可得

3 微分方程建立

由图1微元体几何方程可知，沿z轴的线应变

(16)

根据乌曼斯基第二理论——截面周边不变性的假定，假定εs=0，弹性阶段物理方程满足Hooke’s law[5]20。

(17)

箱形梁在扭转荷载作用下，纵向合力及合力矩为零，根据Saint-Venant假定，可得箱形梁截面的应力边界条件。

∮σ2dA=FN=0

(18)

将式(16)代入式(17)，最后代入式(18)，可得

u′(z,0)=0

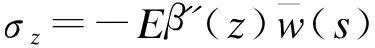
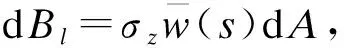
(19)

图3为微元体应力示意图。由图3可得到平衡微分方程(其中体力fz、fs为零)：

(20)

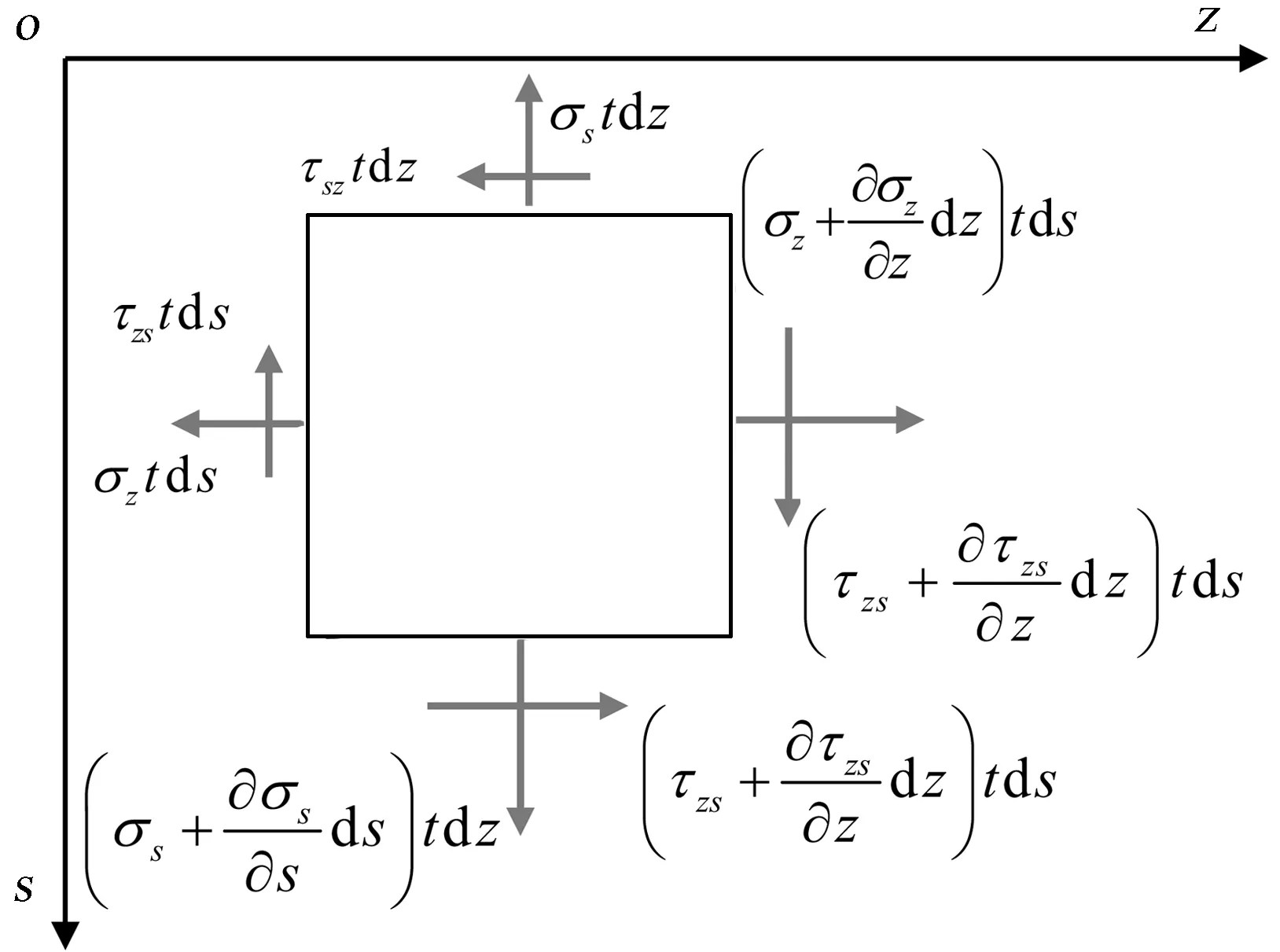
图3 微元体应力示意图

考虑应力边界条件

∮τzshtds=Lk

(21)

由式(20)、(21)得到剪应力τzs的表达式

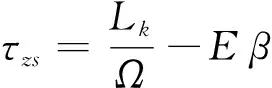
(22)

式(19)、(22)给出了约束扭转作用下箱形梁的纵向翘曲应力σz和约束扭转剪应力τzs的函数表达式，其中翘曲变形系数β′(z)是未知的，根据β′(z)与θ(z)的关系，得出扭转角θ(z)的分布函数。

由公式(2)、(8)可知，v与θ(z)有关，u与β′(z)有关，根据式(1)得到β′(z)与θ(z)的关系。根据Saint-Venant应力边界条件假设，可得到如下微分方程表达式:

(23)

4 微分方程求解

求解微分方程式(23)，可得

(24)

边界条件为

固定端：

θ(z)=0 (截面无扭转)

β′(z)=0 (截面无翘曲)

铰接端：

θ(z)=0 (截面无扭转)

Bl=0 (截面无翘曲应力)

自由端：

Bt=0 (截面无翘曲应力)

β‴(z)=0 (截面无约束剪应力)

以下给出任意扭矩和满铺均布扭矩时截面的各项参数：

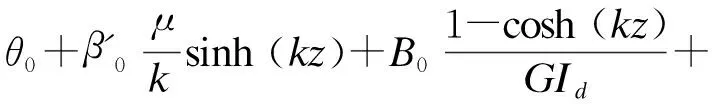
(25)

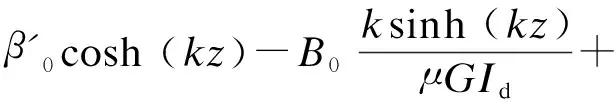
(26)

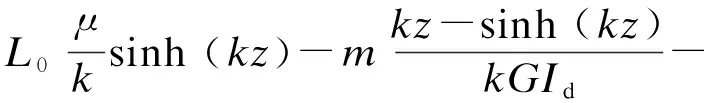
(27)

Lk=l0-Mk-mz

(28)

5 算例

选取跨度L=40 m的等截面单箱单室薄壁箱梁为例，模型截面尺寸见图4，材料的弹性模量E=3.40×104MPa，泊松比μ=0.2。模型满跨布置q=100 kN /m的均布力，偏心距e=2.35m(计算扭转时，可以简化为均布扭矩m=100×3.5 kN)，箱梁边界条件如图5所示。

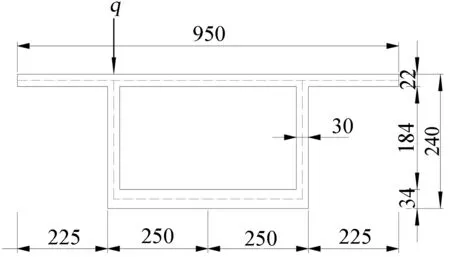
图4 薄壁箱梁横截面图(单位：mm)

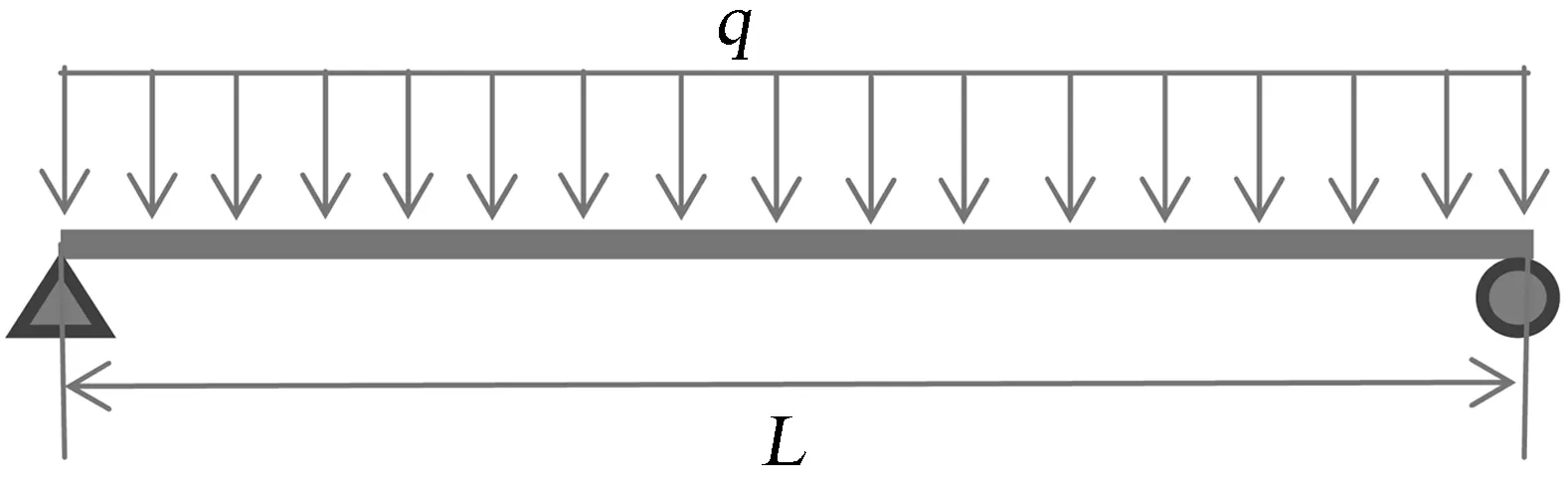
图5 简支梁受均布偏载力

考虑图5所示的边界条件，由式(25)～(28)可得

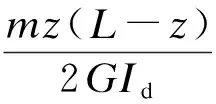
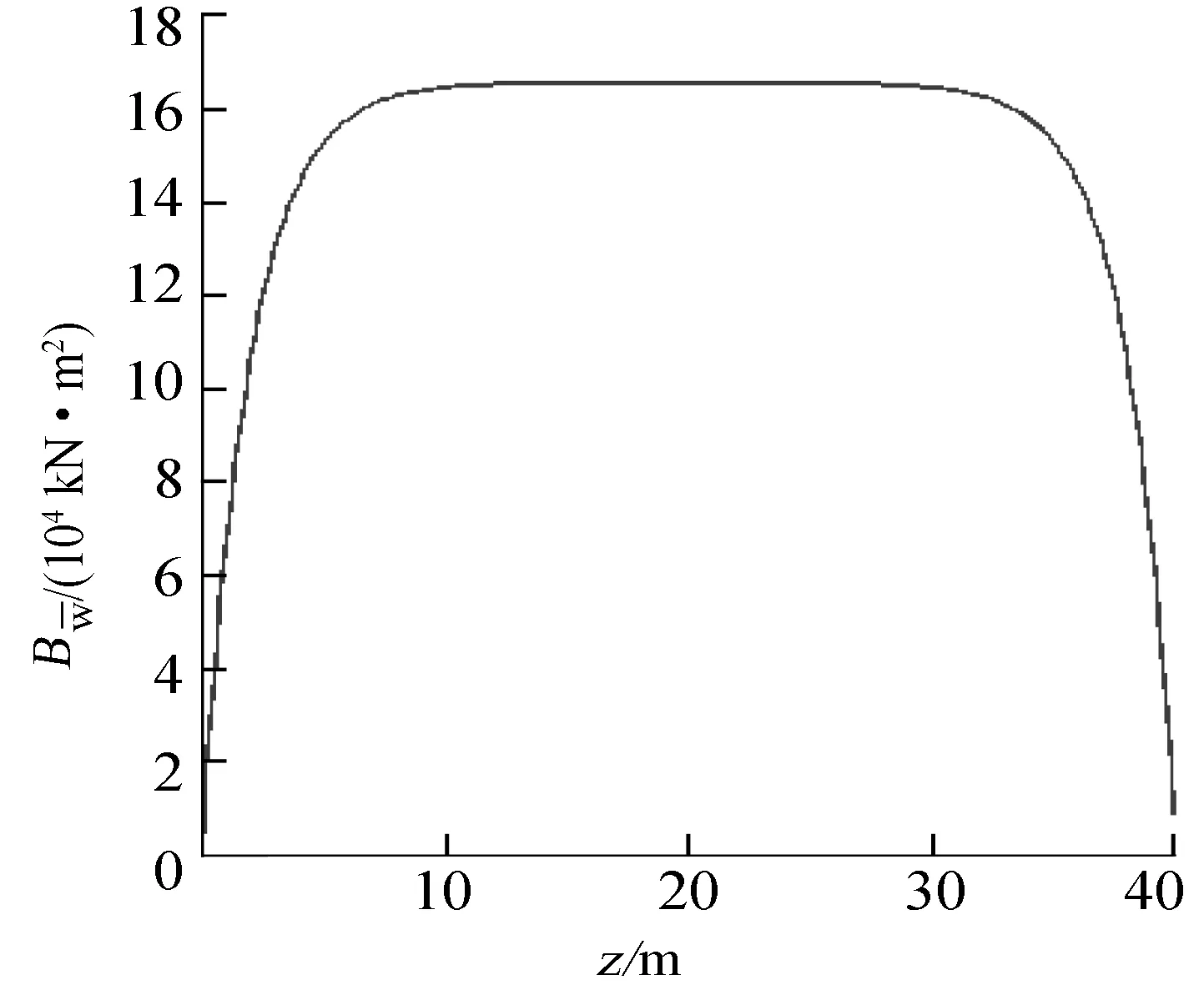
图6 约束扭转双力矩沿梁纵向分布规律

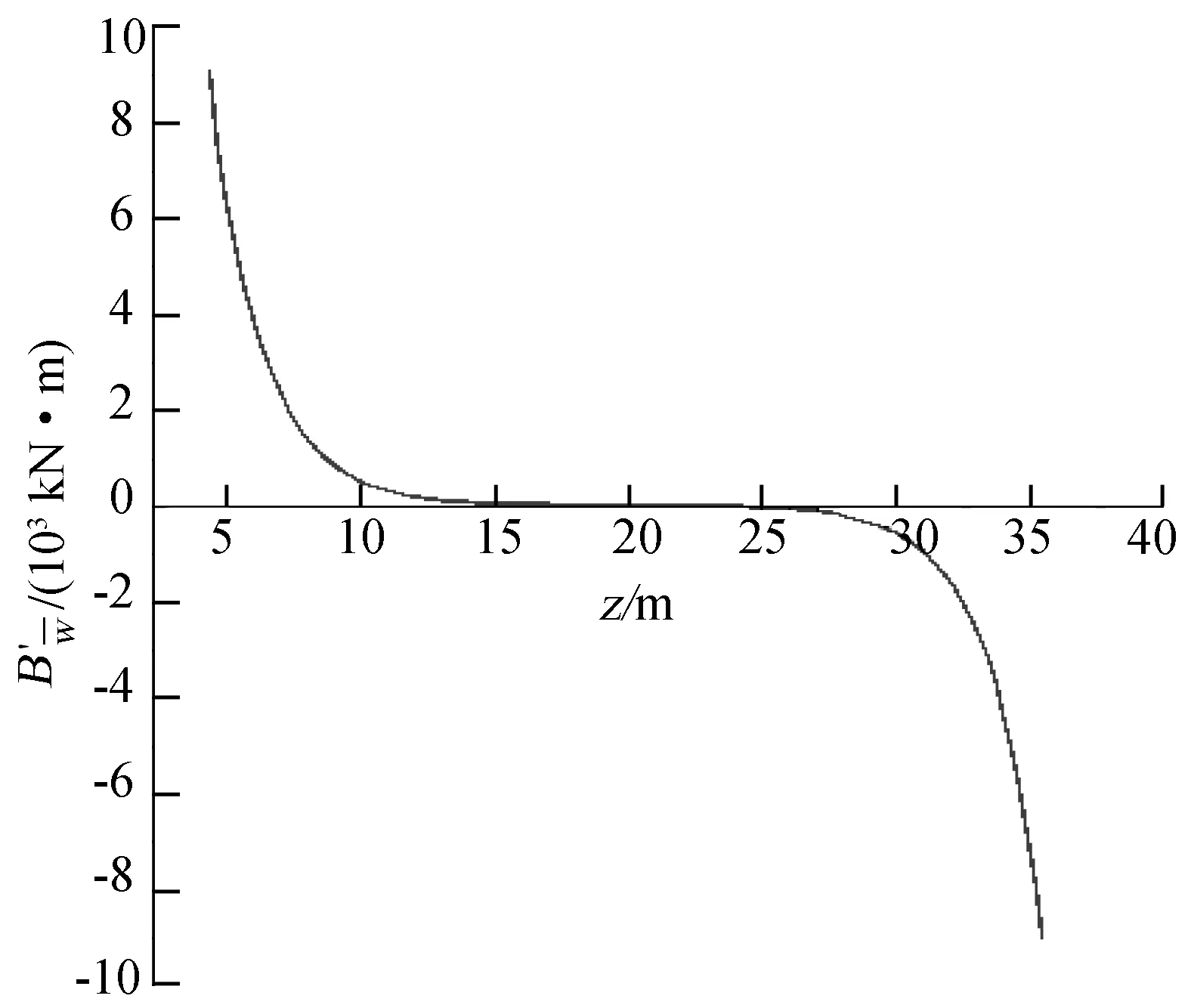
图7 约束扭转双力矩一阶导数沿梁纵向分布规律

由图6、7可见，约束扭转双力矩的分布形式类似于均布荷载作用下的弯矩分布，但在0—L/4断面处变化较为剧烈，而在L/4—L/2处变化相对平缓；约束扭转双力矩的一阶导数在跨中区域为零，在加载端处有最大值，类似于均布荷载作用下的剪力分布规律。

跨中断面处约束扭转翘曲正应力分布，如图8所示。跨中处的自由扭矩与约束扭矩均为零，故剪应力分布为零。

L/4断面处,约束正应力与剪应力分布如图9—10所示。由图8—10可见：L/4至L/2断面的约束扭转翘曲正应力分布规律大致相同，这是因为约束扭转双力矩分布较为平缓，而广义扇形矩和扭转惯性矩与截面有关，本文所选算例为等截面分布，因此约束翘曲正应力在L/4至L/2区域变化不大；L/2断面处自由扭矩与约束扭矩分布均为零，故在该断面的剪应力分布为零，即无剪应力；均布荷载作用下约束扭矩与自由扭矩幅值相差较大，约束扭矩对约束剪应力的分布可以忽略，图10中剪应力在箱梁截面的分布较为平缓，表明约束扭矩的影响较小，在计算过程中已被忽略。

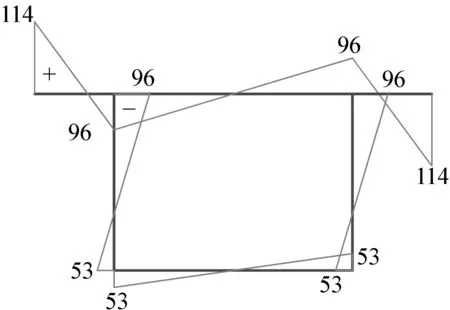
图8 跨中断面约束扭转翘曲正应力分布(单位：kPa)

图9 L/4断面约束扭转翘曲正应力分布(单位：kPa)

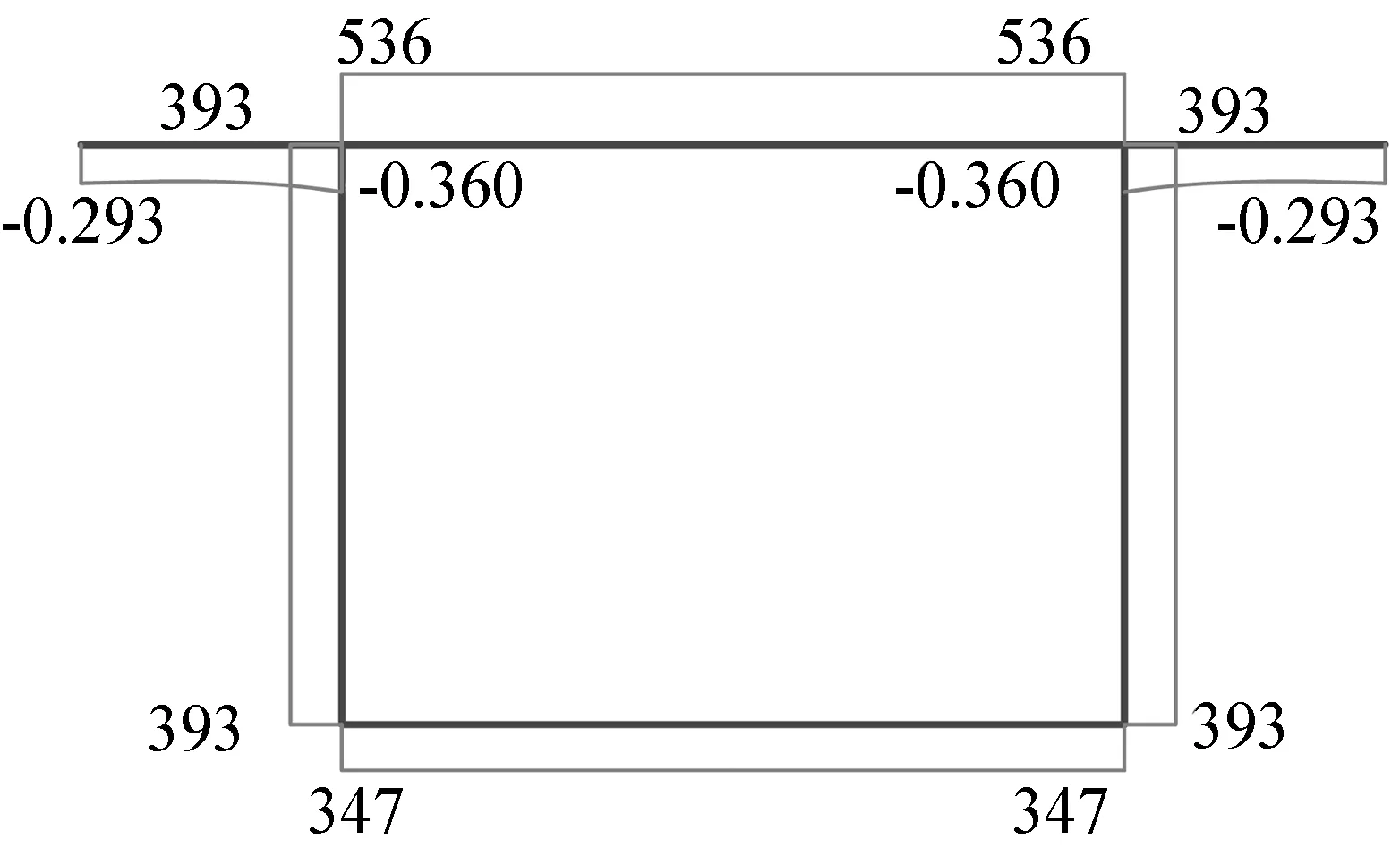
图10 L/4断面约束扭转剪应力分布(单位：kPa)

6 结论

1) 本文基于微元体平衡方程、几何方程、物理方程，在弹性体假设的前提下，推导了单箱单室箱形梁约束扭转的计算方法。

2)均布偏心荷载作用下约束扭转双力矩沿梁轴向的分布与均布荷载作用下弯矩沿梁轴向的分布类似，约束扭转双力矩的一阶导数沿梁轴向的分布与均布荷载作用下剪力的分布类似。

3)均布偏心荷载作用下，约束扭转翘曲正应力对箱形梁的影响较小，经计算顶板最大翘曲应力值与弯矩应力值相差2.68%，底板最大翘曲应力值与弯矩应力值相差1.04%，其影响可以忽略不计；约束扭转引起的剪应力与自由扭转剪应力相比，可以忽略不计。