基于云数据的自助式服务定价模型分析

吴奇,荆江雁,章琦,朱玉洁

(常州工学院数理与化工学院,江苏 常州 213032)

0 引言

在互联网不断发展的背景下，一种新的合作模式——众包(Crowdsourcing)越来越流行。2005年中国学者刘锋提出“威客”一词，而杰夫·豪(Jeff Howe)于2006年在《连线》杂志中首次提出“众包”的概念，威客与众包有着异曲同工之处，都是指企业通过互联网平台发布任务，依靠大众资源为企业提供创意或解决问题的一种创新商业模式[1-2]。这种新的模式在很大程度上避免了生产和需求的脱节，节约了社会资源，使企业的生产和服务更高效。然而，众包模式下也存在悬赏金较低、分配制度不公、交易行为作弊等问题。因此，对众包模式下的数据进行调查统计就成为当下非常热门的研究课题。

陈强等[3](2013)提出竞争情报部门难以应对大数据分析时，可以将期望的指标发布到众包平台上吸引具有数据分析能力的专家参与。牟千[4](2016)分析了移动时代的媒体借助互联网的力量，将众包模式移植于新闻生产领域，变“消费者”为“生产者”。陈卫华[5](2016)提出政府统计调查项目可以借助众包的模式进行，有利于吸引公众参与物价、社情和民意情况调查。

“拍照赚钱”是基于移动互联网的自助式劳务众包平台，为企业提供各种商业检查和信息搜集，相比传统的市场调查方式可以大大节省调查成本，而且有效地保证了调查数据真实性，缩短了调查的周期。用户注册成为会员，领取拍照任务(比如上超市去检查某种商品的上架情况)，赚取酬金。任务定价是否合理是决定任务能否完成的核心要素，如果定价不合理，有的任务就会无人问津，从而导致商品检查的失败。针对这一问题，本文建立数学模型对影响价格的因素进行分析，并对不合理任务定价方案进行重新设计。

1 基于原有定价模型的研究

1.1 研究内容

本文的数据来自2017年全国大学生数学建模竞赛B题[6]。

首先根据竞赛题附件1中已结束的任务数据，将任务定价区间进行分类，绘制了任务点的空间分布图(见图1)。发现这些点基本围绕在广州、佛山、东莞、深圳4市。接着利用K-means聚类算法计算出任务点的聚类中心。

图1 按定价区间分布已结束项目散点图

从图1中可以看出：聚类中心附近的任务定价普遍较低，随着任务位置与聚类中心之间距离的增加，价格随之增加。即任务的定价与任务位置有关，且定价的高低与其到聚类中心的距离总体上呈现正相关关系。

接着根据竞赛题附件2中会员信息数据，将任务点和会员点同时画出，如图2所示。可以看出低定价任务周围其他任务和会员都很密集，高定价任务周围的分布情况相反，即表明任务定价受任务点周围会员密度和任务密度影响，总体上呈负相关关系。

根据上述分析可以看出任务定价受到任务点到聚类中心的距离、任务密度、会员密度的影响，其中任务密度表示某一个任务周围5 km内其他任务的个数，会员密度表示某一个任务周围5 km内会员的个数。

1.2 影响因素相关性分析

首先根据经纬度距离转换公式计算出各个任务点分别到4个聚类中心的距离：

(1)

然后将4个距离值进行比较，选取最小值作为到属于它的聚类中心的距离：

d0=min{d1,d2,d3,d4}

(2)

(a)低定价任务周围会员分布

(b)高定价任务周围会员分布

图2任务点与会员点分布情况

同理，根据式(1)、(2)也可以计算出某一个任务点到各个会员的距离，统计距离小于5 km的个数，完成情况中0表示未完成，1表示完成。截取部分结果如表1所示。

表1 影响因素数据表

1.3 结果

为了得到任务定价和各个影响因素之间的具体相关度，根据相关系数的原理，通过R语言[7]进行相关性分析，并按完成和未完成任务分类，计算出任务定价与各影响因素的相关系数，结果如表2所示。

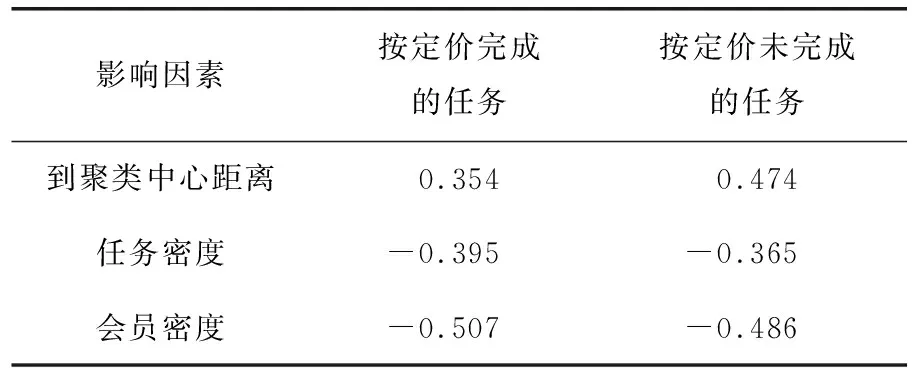
表2 相关系数表

根据前文分析可得如下结论：3个影响因素对任务定价均产生显著影响，任务未完成的情况中，对任务定价影响最大的是任务点到聚类中心的距离，任务所处的位置越远，任务定价越高。

因此任务未完成的原因可能有以下两点。

第一，4市经济发展水平有差异。经济发达地区的会员对任务收益要求较高，导致定价较低的任务无人问津，虽然这些任务附近有较多的会员，但价格对会员的吸引力不足，导致任务未完成。

第二，任务位置偏僻。虽然任务定价较高，但距离聚类中心较远，性价比不高从而导致任务未完成。

2 新定价方案研究

2.1 模型建立与求解

采用多元线性回归分析的模型[8-9]来进行分析。

根据第一部分的分析，选取到聚类中心的距离、任务密度、会员密度这3个因素作为解释变量，定价作为因变量建立多元线性回归模型来进一步改进任务定价模型，得到定价与上述3个指标之间的关系，分析出定价的主要影响因素。建立以下任务定价模型：

y=β0+β1x1+β2x2+β3x3

(3)

其中：x1表示距离；x2表示任务密度；x3表示会员密度。

将表2中的数据代入多元线性回归模型中计算，得到

y=71.67+0.14x1-0.34x2-0.08x3

(4)

2.2 模型结果

从式(4)可以得出：任务定价随着距离的增加而提高；会员密度与任务密度增大时，定价降低；会员密度相对任务密度的影响较小。将未完成任务的3项指标代入模型中计算得到新的任务定价，见表3。

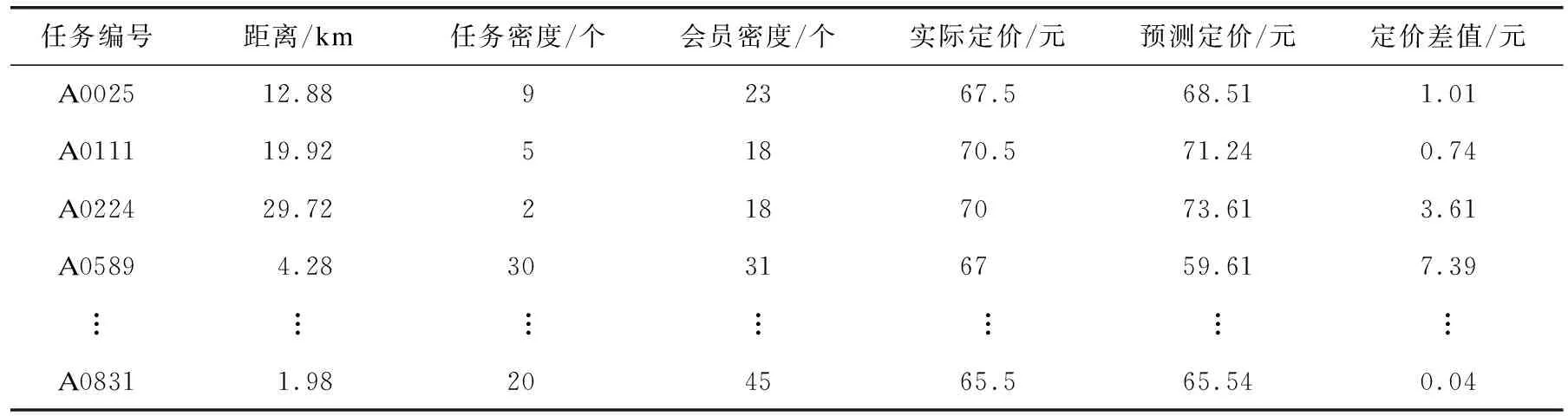
表3 未完成任务的预测定价

假定当预测定价与实际定价差值不超过2元时，即认为该任务完成(例如表3中的A0025、A0111、A0831等)。据此已结束任务中符合条件的任务个数增加117个，计算过程如图3所示。

图3 完成率计算

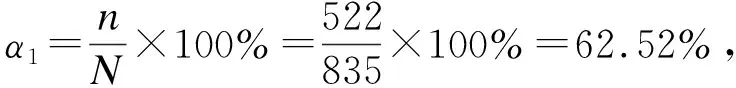
3 讨论

本文在分析未完成任务时，将任务点的经纬度转换为任务点到任务聚类中心的距离，并用图表等形式使分析结果可视化，可以直观看出定价与影响因素的关系。但由于实际定价时，影响因素有很多，而本文研究的数据有限，定价不能准确合理地给出，与实际情况存在偏差，还需做进一步研究。

本文模型的建立基于移动互联网的自助式劳务众包平台，与其类似的服务还有外卖、打车等，都涉及任务位置信息，会员信息等数据，可加以推广应用。