DC/DC变换器并联系统混沌现象的控制策略
丁烨,葛芦生,吴津庆,张瑞
(安徽工业大学电气与信息工程学院,安徽 马鞍山 243032)
0 引言
DC/DC变换器是强非线性电路系统的一部分,改变其内部参数容易引起混沌现象[1-5]。Buck变换器是最早用作研究非线性现象的功率变换器。2000年,Iu和Tse研究发现了并联Buck变换器在主从均流控制下会出现倍周期分岔现象[6]。文献[4]建立Buck-Boost变换器的迭代映射模型,研究电路参数变化时的分岔现象,通过仿真验证了系统状态可能会受到分岔变量的影响。文献[5]分析了负载内阻对Buck系统分岔和混沌的影响,通过仿真得到以电阻值为自变量的分岔图,并对系统3种不同状态进行相图分析,最终采用参数扰动实现了混沌控制。文献[7]通过分析Buck变换器周期轨道及稳定性,论证了系统输出发生倍周期分岔及混沌现象与输入电压变化有关。文献[8]论述了采用自主均流法控制的并联Buck变换器的稳定性,主要研究均流环对系统的影响。
近年来,研究者们提出了很多混沌控制方法。延迟反馈控制(TDFC)可以有效地将混沌系统控制在原来稳定周期轨道[9]。文献[10]首先采用延迟反馈对Buck变换器的混沌现象进行控制,但其针对的是单个Buck建模并且仅分析了延迟时间为开关周期的情况。文献[11]介绍了利用延迟反馈法控制最大电流模式下的高阶并联Boost电路的混沌现象。
本文的研究对象是采用主从均流与电压电流双闭环PI控制相结合的并联DC/DC Buck变换器。通过分析,找到合适的模型——离散映射模型。对处于混沌状态的系统采用延迟反馈控制,分析Jacobian矩阵特征值,求解能够使系统达到稳定单周期态的TDFC增益的取值范围,给出TDFC法控制混沌的可能性。最后通过MATLAB/Simulink仿真和FPGA实验进行结果验证。
1 理论分析
图1为系统控制结构框图。主、从模块Buck变换器的基本结构及参数取值均相同,通过计算得到满足要求的系统参数如表1。
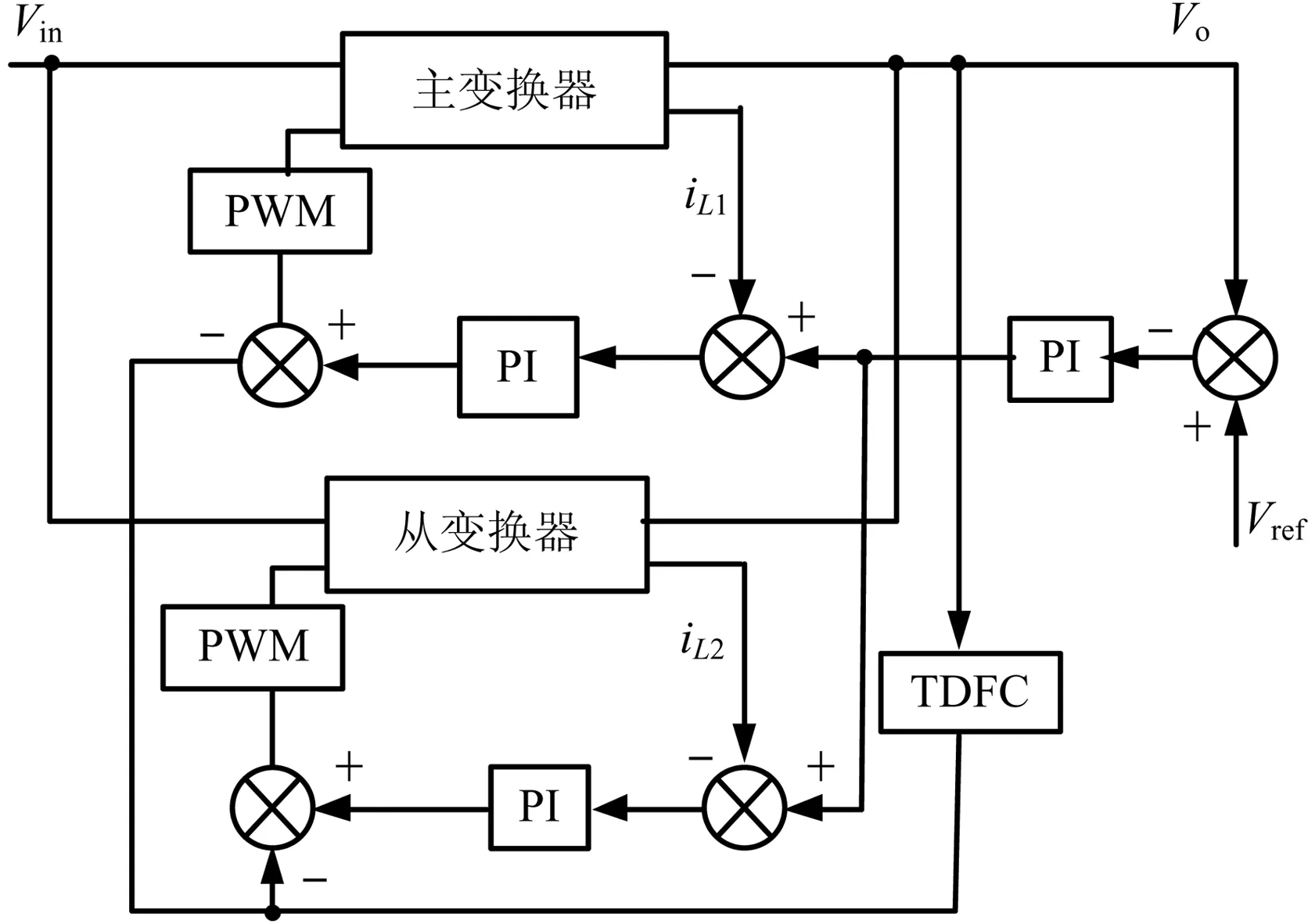
(a)电路控制结构图
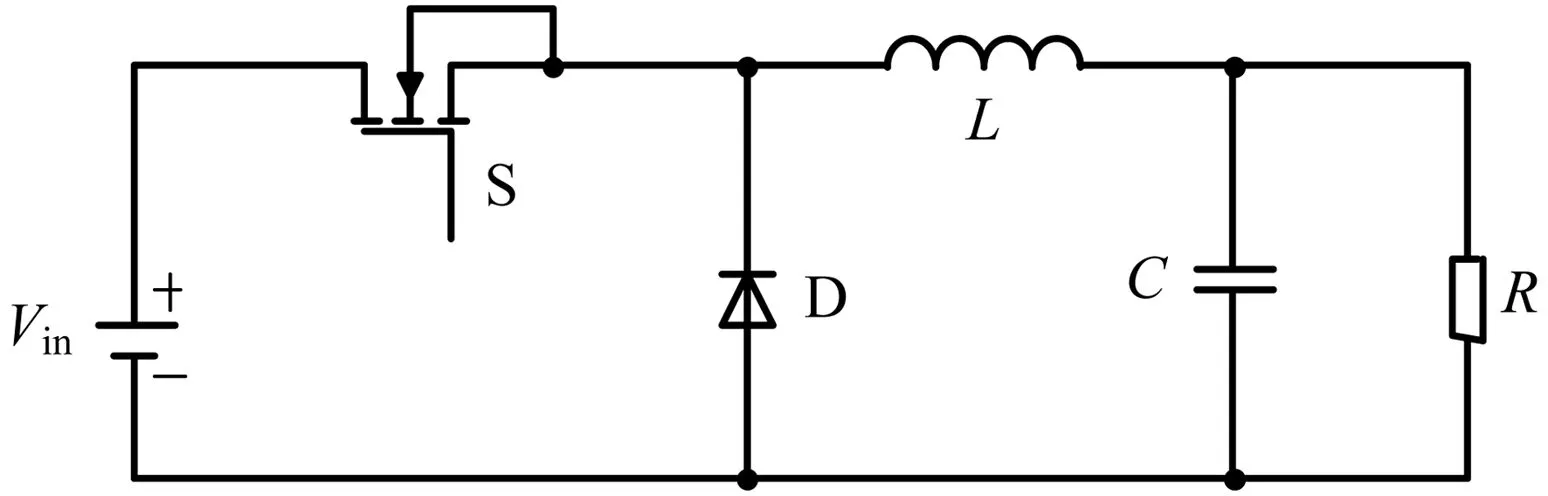
(b)主拓扑结构图1 电路控制框图
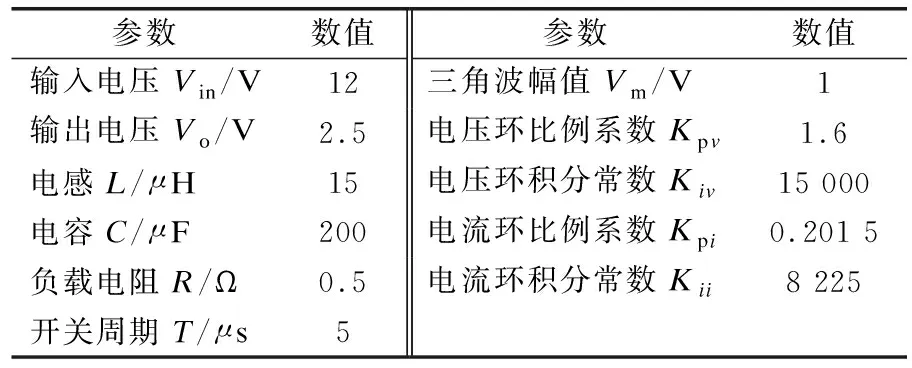
表1 系统参数
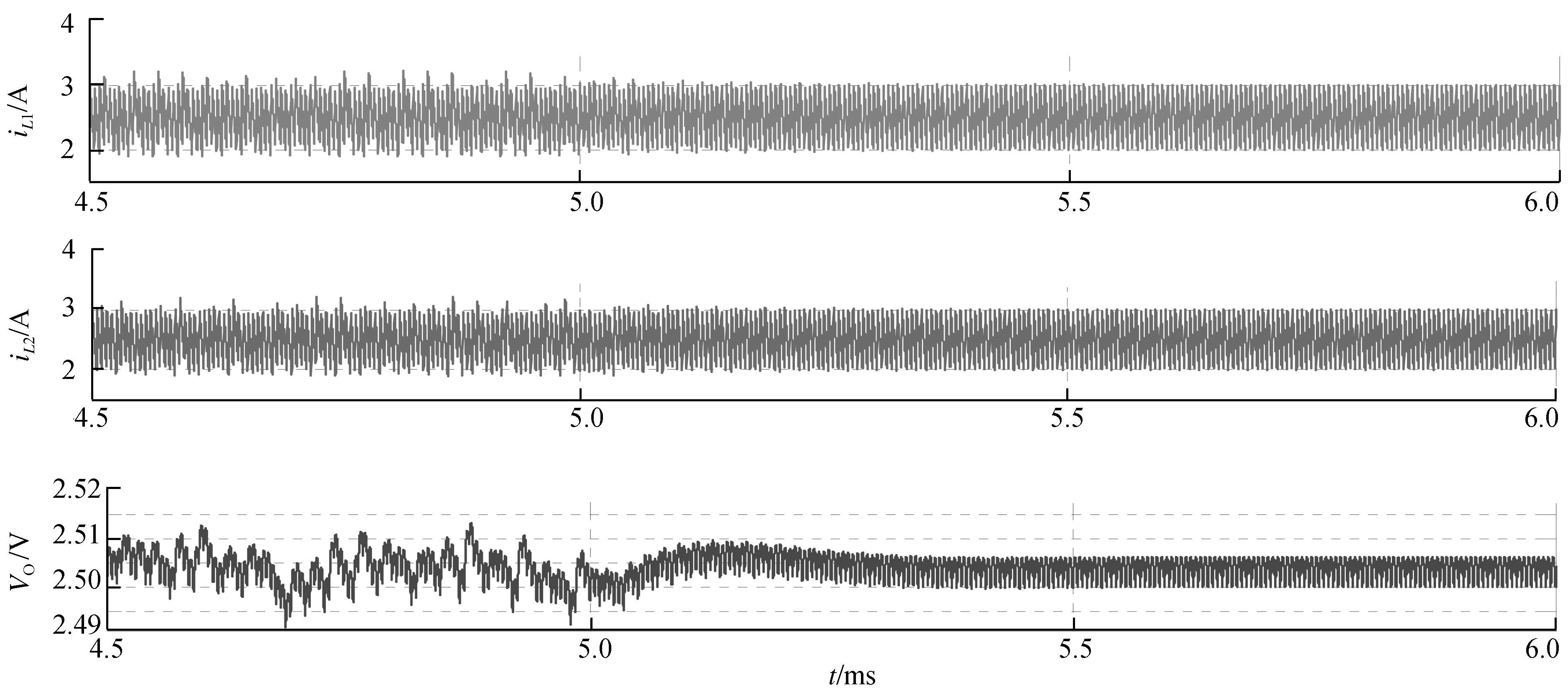
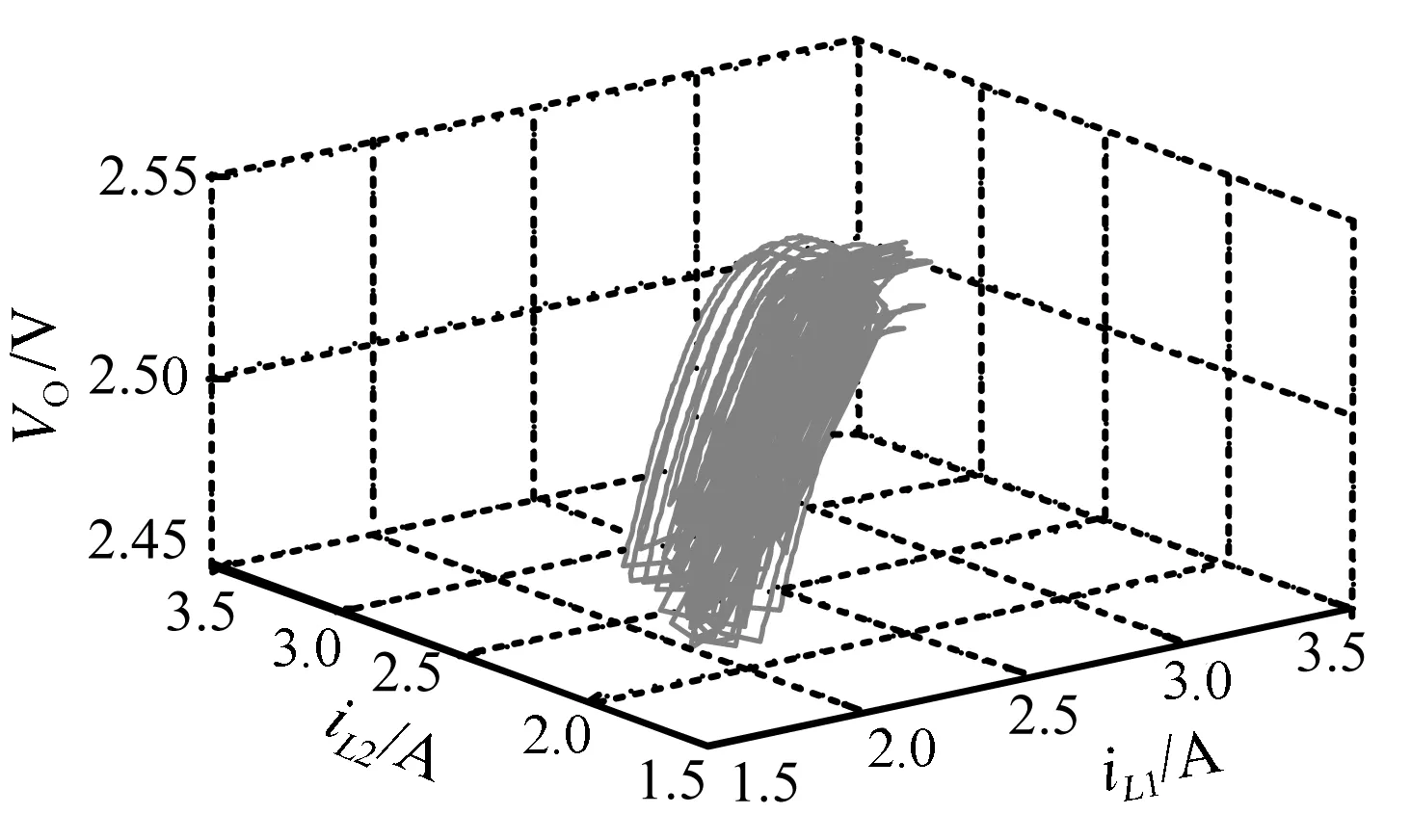
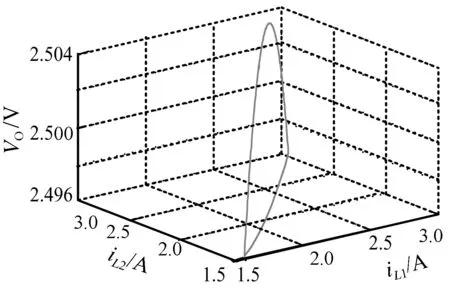
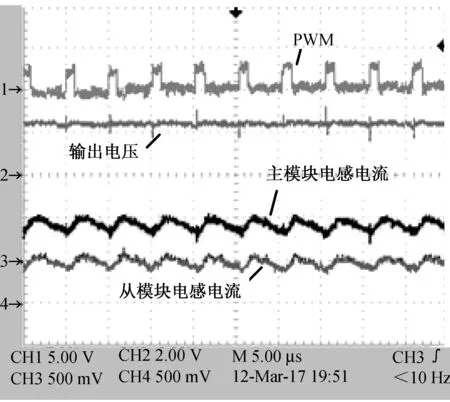
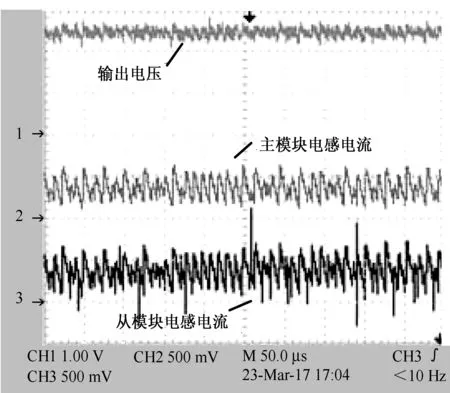
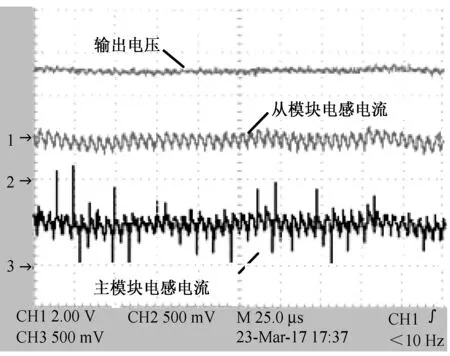
假定主从模块Buck变换器处于电感电流连续(CCM)的工作模式,那么在主模块和从模块中,各模块开关管与二极管总是工作在互补导通状态。主、从模块开关管分别用S1和S2表示,主、从模块二极管分别为D1、D2。每个开关周期中会有4种可能的开关状态,根据开关导通顺序,开始时S1、S2同时导通,结束时S1、S2同时关断,中间的两个开关状态(S1导通、S2关断和S1关断、S2导通)不能同时存在。系统的开关状态主要取决于主、从模块占空比d1和d2,当d1=d2时,系统处于稳定状态。在此设定d1 (1) 式中:x(t)=[uC(t)iL1(t)iL2(t)]T,为状态变量;A1、A2、A3和B1、B2、B3均为状态方程的参数矩阵。 由状态转移矩阵[12]可将式(1)变化为 (2) 式中, 对状态变量的描述省略了T,用x(k)表示x(kT),系数矩阵为: 本文采用主从均流法控制并联DC/DC变换器,主要是将主模块的输出电压与基准电压的差值经误差放大器得到误差信号,并将此误差信号作为主从模块电流基准值,与各模块电感电流进行比较得到控制信号,将控制信号分别与2个同步的锯齿波信号进行比较,最终实现2个模块PWM信号上升沿同步,使各个模块输出电流一致。 系统输出会随着参数(电感电流、输出电压或者PI参数等)的变化而表现出不同的动力学行为。本文主要研究随着输入电压的增大,当系统出现混沌时,采用TDFC使系统达到稳定。研究发现,当输入电压达到25 V时,系统输出会出现混沌现象,对混沌系统采用TDFC可以使其工作在稳态。 TDFC的基本思想是把时间延迟误差当作控制信号并利用周期信号的特点来实现不稳定周期轨道(UPO)的镇定。期望轨道的周期为延迟时间τ,随着目标轨道稳定后,延迟误差会减小至零,控制作用随之消失。系统的动态行为一旦偏离了期望的UPO轨道,延迟反馈控制就会起作用。具体的反馈控制框图如图2所示,控制原理表达式为 Δy(t)=Kf[x(t)-x(t-τ)] (3) 式中,Δy(t)为对系统状态变量施加的小扰动,Kf为反馈增益,x(t)为系统状态变量,τ为延迟时间。 在现代化企业的影响下,要实现资金的管理政策,需结合企业所规定的范围,将与之相关的部门全部规划到计划之内,通过执行企业内部控制制度,来保证资金的稳定性,完整性,有效性。设立完整的资金制度,结合企业的实际情况,促进企业稳定性发展,并且控制资金的使用方案,提升企业的内部控管理水平,防范资金链条出现漏洞。 图2 TDFC原理框图 本系统的开关周期T=5 μs,时间极短,在对系统状态方程的系数矩阵进行泰勒级数展开时忽略关于时间的高次项,可得并联Buck变换器的简化离散时间模型为 x(k+1)=(I+AT)x(k)+B1Vind1T+ B2Vin(d2-d1)T (4) 这里取电容电压uC为状态变量x(t),并作为TDFC的反馈变量,延迟时间τ=T=5 μs,对并联Buck变换器混沌系统施加TDFC,主、从模块的PI调节器均采用位置型算法,此时主、从模块的占空比d1、d2的表达式分别为 (5) (6) (7) 为了分析系统的稳定性并计算Jacobian矩阵,需要对原有系统进行一维控制扩展: (8) (9) (10) 当系统处于稳定状态时,有uC=Vo=Vref,d1=d2=D=Vo/Vin,iL1=iL2=Vo/Ro求解满足上述Jacobian矩阵特征值的模均小于1的Kf取值范围,当Kf∈[1.5 2.5],经TDFC可使系统处于单周期稳定状态。本文仿真与实验中取Kf=2,以此来消除原有系统的分岔或者混沌现象,即可通过TDFC实现系统从混沌态到稳定状态的过渡。 为验证TDFC的有效性,本文使用MATLAB/Simulink进行仿真。如图3所示,当输入电压Vin=25 V时,系统会出现混沌现象,随后在t=5 ms时将TDFC投切进系统,系统可以很快由混沌状态被控制到稳定状态。 图3 施加TDFC前后电流、电压波形图 图4为当系统出现混沌时,施加TDFC前后系统主、从模块电感电流以及输出电压之间的相轨迹图。可以看出,通过TDFC可以使系统由混沌状态转变到稳定状态。 (a)施加TDFC前系统的混沌相图 (b)施加TDFC后系统的稳定相图 为了实现所要求的控制功能,本文选用Altera公司的Cyclone IV系列EP4CE30F23C8N的FPGA芯片作为并联DC/DC变换器系统的主从模块控制器的实验平台。主、从模块Buck变换器以及控制器参数见表1,主、从模块参数完全一致。 用示波器采集基于主从均流控制策略和双闭环PI控制的并联Buck变换器的稳态实验波形,如图5所示。CH2通道显示波形验证系统的输出电压稳定在所要求的2.5 V左右。主、从模块的电感电流(分别由CH3、CH4通道采集)平均值都是2.5 A,实现了均流。主从模块开关管的门极信号(由CH1通道采集)与相应模块的电感电流即输出电流一致,并且从模块跟随主模块变化。 图5 并联系统稳态实验波形 图6为示波器采集到的出现混沌现象以及施加TDFC之后系统的实验波形。其中,图6(a)为当输入电压为25 V时系统出现混沌现象的波形(水平方向每格表示50 μs),可以看出系统的输出电压(由CH1通道采集)以及主、从模块电感电流(分别由CH2和CH3通道采集)的纹波明显比稳态时大,而且呈现出明显的混沌现象,但是整体在稳态值附近变化;图6(b)为在输入电压为25 V时系统出现混沌时施加TDFC之后的实验波形(水平方向每格表示25 μs),可以看出系统的输出电压(由CH1通道采集)以及主、从模块电感电流(分别由CH2和CH3通道采集)的纹波均比混沌状态时小,而且变化更有规律,达到了较好的控制效果。 (a)系统发生混沌现象时实验波形 (b)施加TDFC后的实验波形图6 施加TDFC前后系统实验波形 本文建立了基于主从均流和双闭环PI控制的并联Buck变换器离散映射模型,结合延迟反馈控制研究并联DC/DC变换器的混沌现象。仿真与实验结果初步证明,当系统出现混沌时可以通过TDFC有效地把系统控制到稳态。本文采用的方法具有良好的通用性,可以扩展到多个变换器并联或者是其他变换器拓扑结构中。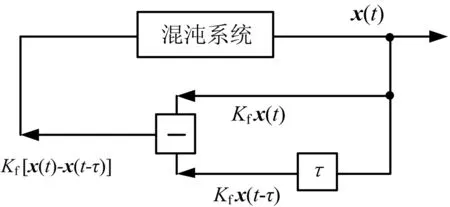
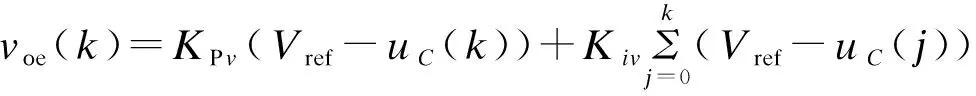

2 仿真分析
3 实验研究
4 结论

