基于动力学系统的状态估计算法

赵天骐，江晓东，李 鹏，白 浩，于 力

（1.天津大学电气自动化与信息工程学院，天津 300072；2.南方电网科学研究院有限责任公司，广州 510080）

电力系统状态估计是能量管理系统EMS（ener⁃gy management system）的主要功能之一，在监测和控制电力系统的可靠运行方面发挥着重要作用。状态估计器通过电压、电流、线路功率、注入功率等测量来估计整个系统的状态，即每个母线的电压幅值和相角。这些测量由数据采集与监视控制系统的远动终端提供。状态估计结果为其他EMS功能，如安全分析、最优潮流、电压稳定性分析等提供基础。因此状态估计的收敛性是电网在线实时监测和控制的关键。

基于高斯-牛顿迭代法的加权最小二乘WLS（weighted least squares）算法是最常用的状态估计算法。然而牛顿法对初始值比较敏感，初始点选择不当会造成算法发散，尤其在以下的情况难以获得状态估计解：

（1）如果测量系统中出现严重的测量错误或电网数据中有拓扑错误，基于牛顿迭代法的WLS估计器可能会发生不收敛；

（2）如果系统中含有不可观测的状态变量，这时增益矩阵会发生奇异，传统基于牛顿迭代的WLS算法将无法进行计算。

从数值的角度来看，当存在很大的注入测量或者采用很大的权值时，状态估计问题可能会出现病态。正交变换法[1]可以在一定程度上解决病态问题。Peters-Wilkinson方法[2]在求解速度和数值稳定性之间进行了很好的平衡。Hachtel增广矩阵法[3]和Cholesky分解法[4]也在克服数值病态问题上有重要贡献。文献[5-6]指出正交分现震荡发散而能给出状态估计的解，提出了基于信赖域（trust region）的状态估计算法来克服这个问题。

本文提出基于动力学系统的状态估计算法，基本原理是将状态估计问题转化为求解非线性动力系统的稳定平衡点SEP（stable equilibrium point），通过构造商梯度系统QGS（quotient gradient system），使其退化的稳定平衡流形对应于WLS的解，从非线性动力学系统理论出发，证明了这个动力学系统是渐进稳定的，因此通过对QGS进行轨迹追踪，可以得到状态估计的解。由于所提出的方法不需要对增益矩阵进行求逆，因此能够克服传统WLS算法的局限性。

1 电力系统状态估计问题

WLS算法是电网状态估计最常用的方法，其实现简单并且计算速度快。该方法旨在找到测量值与其对应测量方程之间的最佳拟合，从而确定出系统的状态变量。由于潮流方程是非线性的，因此状态估计问题也是非线性最小二乘问题。定义以下的列向量。

对于一个有N个节点的电力网络可表示为

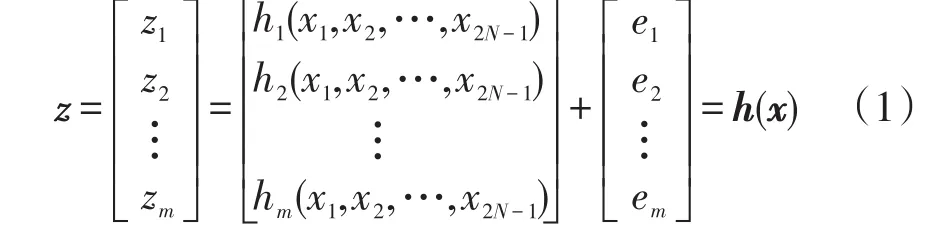
式中：z为测量向量；x为系统的状态变量；h(x)为测量方程；hi(x)为关于测量i的非线性测量方程；e为测量误差列向量。

最小二乘估计是目标函数J(x)的最小化问题，可表示为

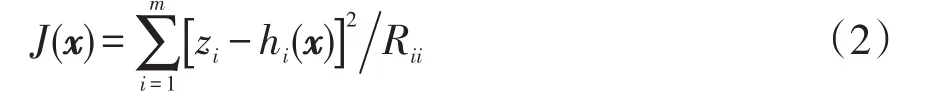
式中，Rii为测量误差方差矩阵的对角元素。

以上最小二乘状态估计问题通常采用高斯-牛顿法求解一阶最优条件，可表示为

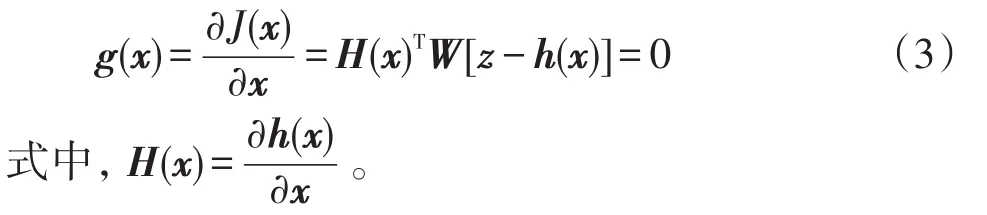
迭代方程由g(x)的一阶泰勒展开并忽略高阶项导出为

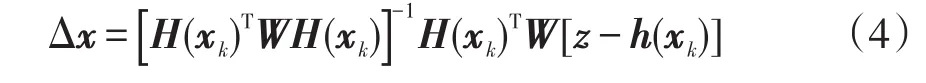
式中：Δx为迭代步长；xk为第k次迭代后的状态变量。

增益矩阵G可以表示为

式中，R为测量误差方差矩阵。

高斯-牛顿法的收敛取决于增益矩阵G是否可逆，也就是说必须有足够的测量分布在整个网络上，从而可以推断出2N-1个状态变量的信息。当有足够的测量用于所有状态变量时，称该系统为可观测的。一个可观测系统的状态可以用测量来唯一地确定，然而测量并非总是在整个网络中均匀分布。系统的一些子区域可能会因为测量不足或测量丢失而导致失去可观测性。在这种情况下，传统的高斯-牛顿法就不能给出状态估计的解，而对于不可观测的系统，状态估计的解不唯一。

2 基于动力学系统的状态估计算法

基于动力学系统的方法基本思想是将状态估计问题转化为适当构造的动力系统，状态估计的解可以通过求解对应动力系统的稳定平衡点来得到。因此，动力系统的构造和性质是该方法的关键。首先介绍非线性动力系统的一些基本概念。

2.1 非线性动力学系统概述

非线性自治动力学系统可以表示为

式中：F:ℜn→ℜm为从ℜn空间到ℜm空间的映射；为状态变量x的一阶导数。定义动力学系统的轨迹为t=0时刻起从x0出发的曲线，记作

下面介绍平衡流形和稳定平衡流形的定义，以及相关的定理。

定义1 平衡流形：对于动力学系统式（6），称Σ={F (x)≡0|x∈ℜn}为该动力学系统的一个平衡流形。即平衡流形Σ上的任意一点x都满足F(x)=0。

定义2 稳定平衡流形：若对于任意ε＞0，存在δ=δ(ε)＞0 ，使对于任意的 x∈Bδ(Σ )，有 Φ(t,x)∈Bε(Σ )，其中 Bδ(Σ)={x ∈ ℜn|‖x-y‖＜δ,∀y∈Σ }，则动力学系统式（6）的平衡流形Σ是渐近稳定的，称作稳定平衡流形SEM（stable equilibrium mani⁃fold）。反之，平衡流形Σ是不稳定的，称作不稳定平衡流形UEM（unstable equilibrium manifold）。

定理1 设动力学系统的平衡流形Σ和任意一点x∈Σ，DF(x)为F在x处的雅可比矩阵。若DF(x)在正规空间Nx(Σ)上的特征向量（所有不在切空间上的特征向量）所对应的特征值的实部都为负值，则x是稳定的，Σ为稳定平衡流形。若DF(x)在正规空间Nx(Σ)上的特征向量所对应的特征值至少有一个含有正实部，则x是不稳定的，Σ是不稳定平衡流形。如果有k个含有正实部的特征值，称Σ为k型不稳定平衡流形（type-k UEM）。

2.2 理论基础

考虑如下QGS[7]：

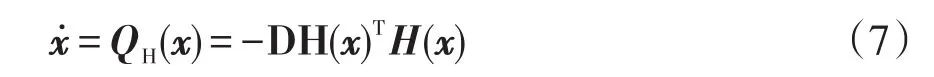
式中，DH(x)为 H(x)的雅可比矩阵，H(x)=[z -h(x)]。

定理2 动力学系统式（7）的一个稳定平衡流形 Σs是函数E(x)=‖H (x)‖22的一个局部最小点。

证明：

设Σs是动力学系统式（7）的稳定平衡流形，因此存在一个 ε＞0使得对任意的y∈Bε(Σs)，其轨迹Φ(t,y)→Σs。因为函数 E(x)=‖H(x)‖22 沿着轨迹的导数 E(x)=-‖DH (x)TH(x)‖2≤0是非正的，也就是说对于任意的y∈Bε(Σs)，E(x)是一个非增函数，即Σs是下面最小化问题的一个局部最优解：

定义3 退化稳定平衡流形DSEM（degenerat⁃ed stable equilibrium manifold）：动力学系统式（7）的一 个 稳 定 平 衡 流 形 Σs，若 H(Σs)≠0 且DH(Σs)TH(Σs)=0，则称 Σs为退化稳定平衡流形。

由于测量误差的存在以及测量在局部具有一定的冗余度，根据定理2和定义3，动力学系统将只存在退化的稳定平衡流形，并且该退化的稳定平衡流形是函数E(x)=‖H (x)‖22的一个非零局部最小点。这里2E(x)=Hs(x)THs(x)即为最小二乘准则的目标函数。若将Hs(x)中的约束乘以权值其中测量i的标准差σi反映了对应测量的精确度，则有E(x)=Hs(x)TWHs(x)，这时WLS的解便为QGS的退化稳定平衡流形。因此，可以通过对QGS进行轨迹追踪，得到其退化稳定平衡流形上一点，从而得到WLS模型的状态估计解。

下面讨论DSEM的维数与状态估计中不可观测状态变量维数之间的关系。设集合ΣDSEM为QGS的退化稳定平衡流形，如果ΣDSEM中的每个点对应的H(x)值不同，那么集合ΣDSEM在ℜn中的Lebesgue测度为0。定理的证明见文献[8]。

当状态估计问题中系统的网络结构和测量能够保证系统的可观测性时，定理3中的假设是满足的。因此对应QGS的退化稳定平衡流形，即WLS的解是孤立的点。然而，当状态估计问题中出现不可观测变量时，由于不可观状态量的取值对WLS目标函数值没有影响，因此定理3中的假设不能满足，此时给出下面的定理。

定理4 设系统中含有k个不可观状态变量，那么QGS动力学系统的退化稳定平衡流形ΣDSEM的维数为k。

证明：

设x为退化稳定平衡流形ΣDSEM上一点，因此x=QH(x)=-DH(x)TH(x)=0。设系统中有k维不可观测状态变量，由于不可观状态量的取值对QH(x)的值没有影响，则存在映射Ρ:U→ℜn，其中U是ℜk中的一个开集，满足QH[ ]Ρ(s)≡0，s∈U。因此ΣDSEM={Ρ (s)|s∈U }为一个k维平衡流形。证毕。

定理4说明当状态问题中含有k维不可观测变量时，对应QGS的退化稳定平衡流形也是k维的，在k维退化稳定平衡流形上的任意一点都可以使WLS目标函数最小，因此WLS不具有唯一解。这时QGS收敛到退化稳定平衡流形上的哪一点将和初始值有关。

2.3 算法流程

根据上面阐述的理论基础，本节给出基于动力学系统算法求解WLS模型的求解流程，当传统基于高斯牛顿的WLS算法不收敛时，启动基于QGS的状态估计算法，通过对QGS的轨迹进行追踪，得到其退化稳定平衡流形，从而得到WLS估计模型的状态估计解。

步骤1 读入电力系统网络参数和测量数据；

步骤2 生成状态估计测量方程；零注入平衡方程；

步骤3 采用高斯牛顿法求解WLS状态估计问题，如果收敛，输出状态估计结果；否则进入步骤4；

步骤4 并构造对应的QGS如式（7）所示；

步骤5 对QGS的轨迹进行跟踪，采用数值积分方法，求解到QGS的退化稳定平衡流形，收敛判据为‖QH(x)‖＜ε

求解过程中使用的数值积分方法可以采用隐式欧拉法、龙格库塔法等常用的数值方法进行轨迹的追踪。仿真软件Matlab中也提供了多种积分器可供选择，本文的测试算例均采用隐式刚性积分器ode15s。

3 算例分析

3.1 IEEE 14节点测试系统少量测算例

本节给出在IEEE14节点测试系统上进行的仿真结果，图1给出了IEEE14节点测试系统的接线图，以及本算例使用的测量类型和位置。该测试系统状态变量维数为n=2×14-1=27，测量个数为m=36，零注入约束3个，分别是7号母线的有功和无功零注入约束，8号母线的有功零注入约束。所有的测量数据均由已知的潮流解推得，并叠加标准差σ=0.02的随机误差。

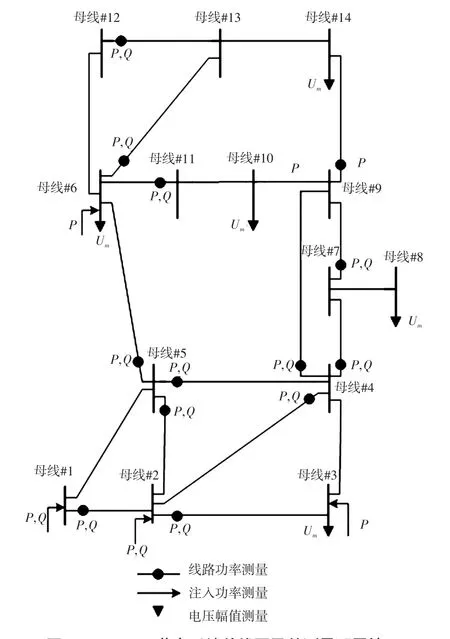
图1 IEEE 14节点系统单线图及其测量配置情况Fig.1 Single-line diagram of IEEE 14-bus test system and its measurement arrangement

该系统存在不可观测状态变量Va10（10号母线的电压相角），这时WLS算法中的增益矩阵奇异，因此传统基于高斯-牛顿法的WLS算法无法计算。按照如上介绍的基于动力学系统的状态估计算法流程，可以求解到QGS的稳定平衡流形，从而得到可观测变量的状态估计解。

初始点设置为平启动（电压幅值为1.0，相角为0°），得到测量残差、状态变量估计误差和收敛过程如图2所示。图2（a）为QGS的收敛过程，横坐标是指积分运算中的时间参数，不是实际计算时间。纵坐 标 为QGS方 程 ‖QH(x)‖，收 敛 判 据 为‖QH(x)‖ ＜10-6。图2（b）为测量残差，图2（c）为估计误差，可以看到除不可观变量外，其他状态变量均有较高的估计精度，估计误差均值为D=0.004 175。本算例中Va10的实际值为-0.264 rad，不可观测变量的估计值和初始点选择有关。

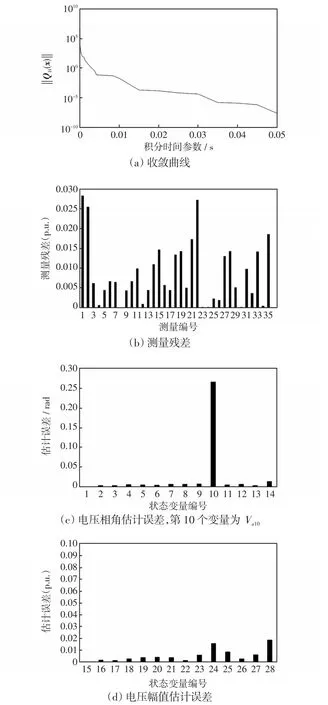
图2 在测量含有标准差为0.02的随机误差时的收敛过程和测量残差以及估计误差Fig.2 Convergence process,measurement residuals and estimation errors when measuring random errors with standard deviation of 0.02

根据定理4，该算例含有1维不可观测变量，则QGS的退化稳定平衡流形也为1维，下面在Va9×Va10×Vm8的3维空间中展示QGS的退化稳定平衡流形以及不同初始点的收敛轨迹。

如图3所示，在Va9×Va10×Vm8的3维空间中随机采样20个不同的初始点，通过对QGS进行轨迹追踪，均收敛到QGS的退化稳定平衡流形上，图3中与Y轴Va10平行的一维曲线。不同的初始值会收敛到退化稳定平衡流形上的不同点。由于不可观变量Va10的取值对WLS目标函数没有影响，因此一维退化稳定平衡流形上的任意一点都可以使WLS目标函数最小。图3中曲线的灰度表示WLS目标函数，数值越小，黑色越深。

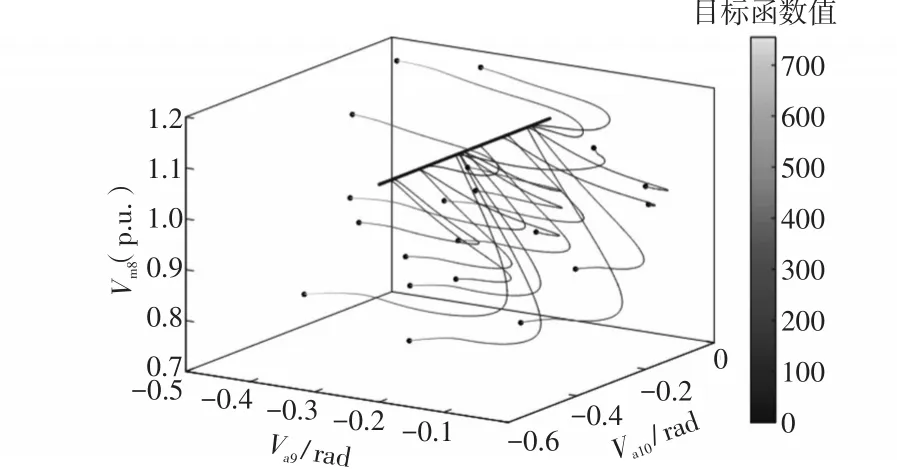
图3 IEEE14节点不可观测测试算例中QGS的退化稳定平衡流形以及不同初始点的收敛轨迹Fig.3 DSEM of QGS for IEEE 14-bus unobservable test system and the convergence trajectory with different initial points

4.2 IEEE 118节点少量测测试算例

下面使用IEEE 118测试系统对基于动力学系统的状态估计算法进行测试。系统中含有54个发电机，186条线路和91个带有P-Q负荷的母线。本算例使用完整的电气量测量一共有1 098个，包括118个电压幅值测量，236个功率注入测量和744个线路首末端功率测量。本节使用的测量均在真实值基础上叠加了标准差为0.05的随机误差。

从全部1 098个量测数据开始，随机地去掉量测直到只剩1个量测，对基于动力学系统的状态估计算法进行测试。显然，当逐个去掉测量时，系统测量的冗余度下降，会有部分测量变为关键量测，如果继续随机地去掉测量，系统会出现不可观状态变量。图4给出了测量数目逐渐减少时，基于动力学系统算法和传统高斯-牛顿法的估计精度对比。当测量数目小于460个时，由于增益矩阵的奇异，传统WLS算法无法获得状态估计解，而本文提出的基于动力学系统的算法能够在系统失去可观测性时提供可以接受的估计值。当然，随着测量的减少，不可观状态变量的增多，估计误差也迅速变大。

当测量数目减少为300个时，经可观测性分析，系统中将有4个不可观测状态变量分别为Va112、Va20、Va38、Vm112。这时WLS算法的增益矩阵奇异，条件数为cond(G)=7.143 9×1019，传统高斯牛顿法不能收敛。图5给出了此时增益矩阵G的特征值。图6给出了QGS的收敛过程。

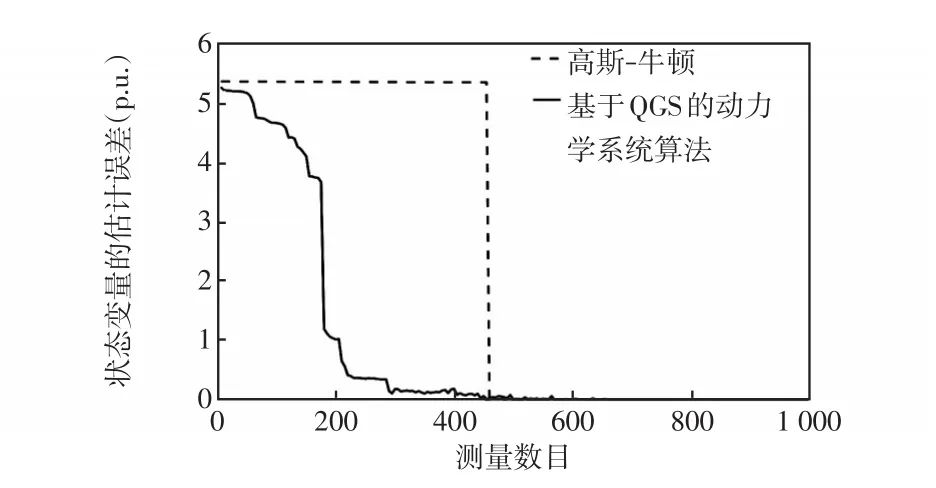
图4 随着测量数目减少，基于动力学系统算法和传统高斯-牛顿法的估计精度对比Fig.4 Comparison of estimation accuracy between the method based on dynamical system and the traditional Gauss-Newton method when the number of measurements is decreasing

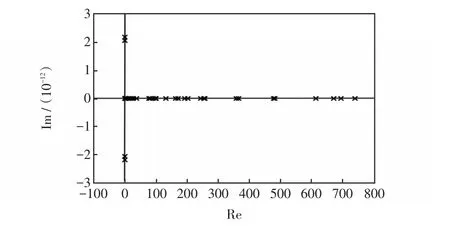
图5 在测量数目减少为300个时，WLS算法中增益矩阵G的特征值Fig.5 Eigenvalue of the gain matrix G in WLS method when the number of measurements is reduced to 300

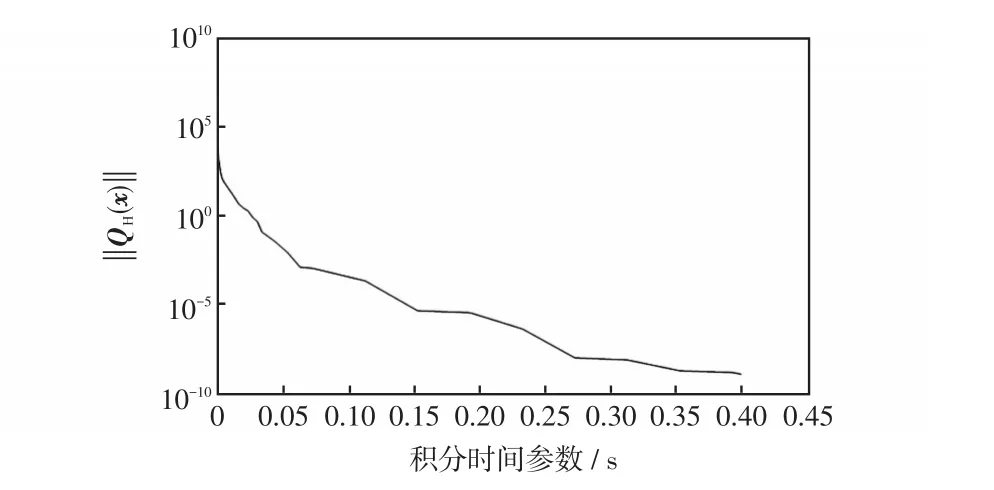
图6 在测量数目减少为300个时，基于动力学系统算法的收敛曲线Fig.6 Convergence curve of the method based on dynamical system when the number of measurements is reduced to 300

3.3 IEEE 14节点存在拓扑错误时的收敛性测试

采用文献[5]中的测试算例，假设6-12线路被认为断开，而实际上这条线路没有断开。该算例有42个测量，包括7个电压幅值测量，11个注入功率测量，24个线路功率测量。

图7给出了IEEE 14节点测试算例含有一个拓扑错误时，高斯-牛顿算法和基于QGS动力学系统算法的收敛曲线对比。上方的横坐标表示高斯-牛顿法的迭代次数，下方的横坐标表示对QGS动力学系统的积分时间参数，可以看出高斯-牛顿法呈现出震荡的现象，未能求解到WLS解。而本文提出的算法可以收敛。

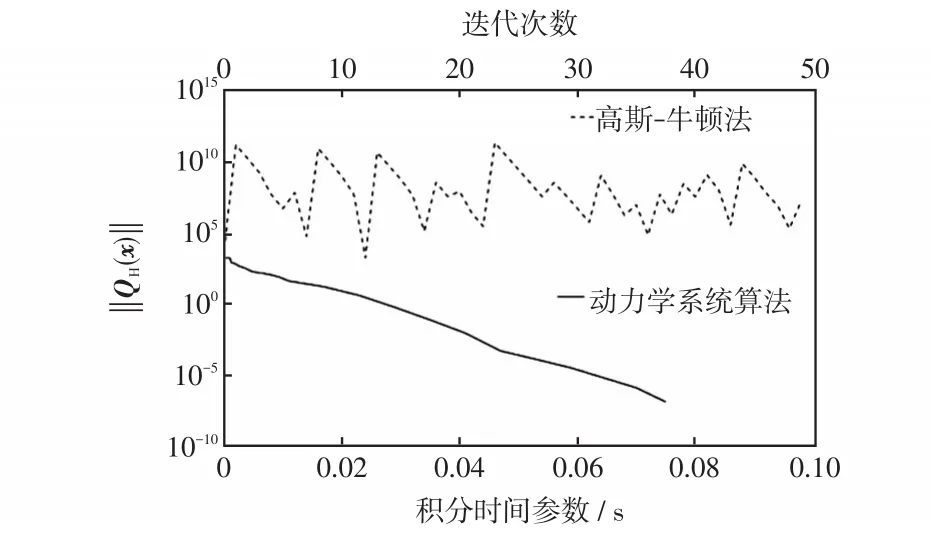
图7 IEEE 14节点测试算例含有一个拓扑错误时，高斯牛顿法和动力学系统算法的收敛曲线对比Fig.7 Comparison of convergence curve between the Gauss-Newton method and the method based on dynamical system for IEEE 14-bus test system with one single topological error

牛顿（或高斯-牛顿）法在初始点接近解时具有优良的收敛速度，但缺点在于对初始点很敏感，因此当状态估计问题中出现很大的测量残差时可能造成求解失败。当测量数据中含有严重的坏数据或者拓扑错误时，往往需要先求解出一个WLS解，然后对残差或标准化残差进行分析，从而对坏数据和错误拓扑进行识别。然而从本算例可以看出，在出现严重错误时，可能造成牛顿法不收敛，从而无法进行下一步的坏数据和拓扑错误识别。本文提出的算法在这种情况下能够保证收敛，为错误测量和拓扑识别提供基础。

4 结语

本文提出了一种新的基于动力学系统的方法来求解状态估计问题，构造商QGS，其退化的稳定平衡流形对应于WLS的解，并证明QGS是渐进稳定的，因此可以保证算法的收敛性。该方法可以可靠地处理因拓扑错误而可能引起的不收敛问题，当系统中存在不可状态变量时，可以继续进行求解并得到有效的状态估计解，同时用数值算例对不可观算例的WLS解进行了刻画。所提出的算法在IEEE 14节点和IEEE 118节点系统上进行测试，验证了其可靠性和有效性。