城市集中型充电站规划方法

冯瑛敏，赵 新，任国岐，赵 晶

（1.国网天津市电力公司经济技术研究院，天津 300191；2.国网天津市电力公司，天津 300010）

当前充电基础设施的不完善已成为制约电动汽车EV（electric vehicle）发展的重要因素，且尤以承担大范围内电动汽车快速充电的城市集中型充电站建设数量不足最为突出[1-2]。作为联系电动汽车用户和电网的桥梁，充电站合理布局可通过合理用电行为促进电能高效利用，还能向用户提供快速便捷的充电服务，实现用户、充电站及电网三者间的友好互动，进而促进电动汽车及其配套行业的快速发展。集中型充电站规划是一个多目标、多变量、非线性优化问题，规划选址时需综合考虑用户充电便利性、配网结构及容量、建站成本等多种因素[3]。国内外众多学者针对这一问题从不同角度进行了研究。

文献[4]采用网格法确定充电站站址；文献[5-6]均以充电站开发建设成本及用户充电成本之和最小为目标函数，建立快速充电站选址定容的混合整数非线性优化模型；文献[7]以俘获的交通流量最大、配电系统网络损耗最小以及节点电压偏移最小为目标建立充电站最优规划的多目标决策模型，并采用数据包络分析DEA（data envelopment analysis）评价方法来确定各目标权重，把多目标优化问题转化为单目标问题求解，但DEA方法本身存在对异常值敏感的不足，可能导致输出结果的不稳定。文献[8-9]中考虑了居民用户的出行活动特征，确定EV充电需求，以EV群体空驶成本最小化为目标进行充电站选址。与之对应的，文献[10]针对城市公共交通（电动公交车和出租车），分析日出行规律，构建了考虑削峰填谷作用的集中型充电站选址定容二层规划模型，并采用改进遗传算法和自适应粒子群算法进行充电站选址计算。

由于考虑城市交通和居民分布环境的充换电站选址问题扰动因素多，求解困难，因此现有方法多以智能算法进行规划，求解最优解。优化过程中存在参数选择依赖于经验，算法复杂度较高的缺点。近年来，聚类算法因其对于大数据集有较高的计算效率和良好的可伸缩性，在充电站规划中得到应用。如文献[11]采用近邻传播算法进行电动公交车换电需求点空间聚类以确定充电站站址及规模。然而，聚类算法对初始聚类中心的选址较为敏感，且最终聚类结果仅为数学意义上的各充电需求点至聚类中心平均距离最小值，难以满足实际场景需求是单纯采用聚类算法的主要缺点。

为克服聚类算法的不足，本文采用图论中央点理论对K-means聚类算法进行改进，计及EV时空分布特点，建立了充电需求点与路网结构的图论抽象模型，采用中央点算法与K-means聚类算法有效结合进行充电站选址和服务范围划分，最后通过某城区实际算例分析对本文所提方法的有效性进行验证。

1 城市集中型充电站选址数学模型建立

城市集中充电站主要供给周边居民的EV，并可为公共交通提供电能供给。充电需求点一般包含有医院学校、大型商超、车站等。考虑各充电需求点间的路网结构情况，基于图论知识可构建集中型充电站选址的无向连通图模型G=（V，E），其中V为各充电需求点vi的集合，E为连接各充电需求点间的道路集合。与传统图结构不同，这里需要考虑道路非直线系数β，β＞1。此外定义vi对应的集中充电量需求量pi为顶点的权值，需求点vi、vj间最短道路的长度βd(vi,vj)记为边的权。由于集中型充电站的首要目标是向EV用户提供便捷的充电服务，故充电站的站址选择问题可数学抽象为寻找图的中央点问题，即确保取最小值时所对应的

中央点集，可表示为

2 集中型充电站规划方法

2.1 规划区分划分计算

首先根据单台充电设备容量及充电设备允许数量的上限、下限确定规划区域内建设充电站数量的上限、下限(Nch_max、Nch_min)。上限、下限的数值计算公式为

对这(Nch_max-Nch_min+1)种规划方案，进行线路潮流、电压偏移等约束条件校验，对满足约束条件的可行方案，基于K-means聚类方法进行充电站服务范围划分，进而在以各服务范围内充电需求点构成子图内计算中央点作为充电站的待建设地点，确定充电站供电接入点，完成最优选址规划。图1为城市集中型充电站规划总体流程。

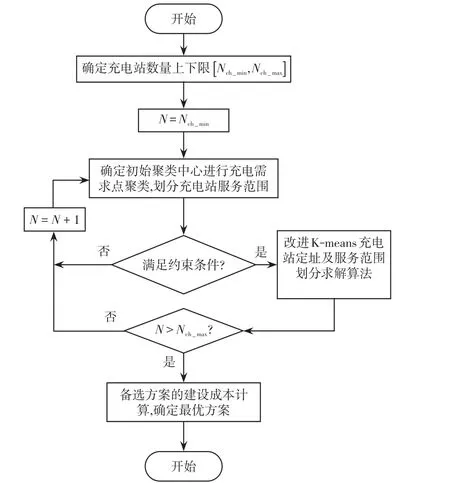
图1 集中型充电站规划总体流程Fig.1 Overall flow chart of planning for centralized charging stations

2.2 改进K-means的集中型充电区域站定址及服务范围划分求解算法

作为硬聚类算法，K-means聚类算法以数据目标点与聚类中心点距离最小为优化目标函数，实现数据的最优分类，其具有算法快速简单、可伸缩、对大数据集分类高效的特点。但在使用中，确定初始聚类中心的选择对聚类划分结果有较大影响[12]。因此本文结合图论中央点理论实现对K-means聚类算法的改进，实现充电站服务区域划分和充电设施最优选址，具体算法流程如下。

步骤1 利用地理信息系统GIS（geographic in⁃formation system）获取规划区域内充电需求点坐标，建立城市集中充电规划无向连通图模型G=（V，E）。并依照式（2）计算在待规划区域内的充电点需求数目范围[Nch_max,Nch_min]。

步骤2 基于K-means聚类算法对规划区域充电需求点进行聚类划分，聚类个数m∈[Nch_max,Nch_min]。在每个聚类划分子区域采用图中央点算法计算子区域中央点。

步骤3 设当前进行第k次聚类，在全网络中按式（3）计算各充电需求点vi到初始聚类中心的行驶距离，按照最邻近原则对各需求点进行新K-means聚类划分，形成第k+1次聚类。行驶距离可表示为

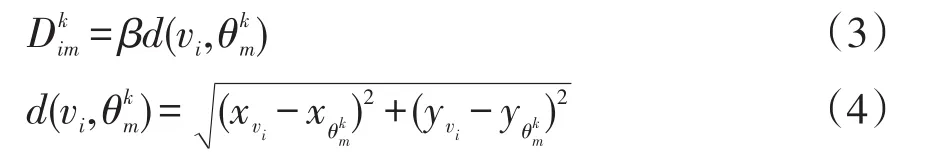
式中：d(vi,)为充电需求点到初始聚类中心的欧氏距离；(xvi,yvi)、(xθkm,yθkm)分别为充电需求点及初始聚类中心的坐标。

步骤4 在新聚类划分规划区域m内再次采用图中央点算法计算子区域中央点。计算各充电需求点vi到初始聚类中心的行驶距离验证两次行驶总距离差是否满足收敛条件，收敛条件可以表示为

式中：ε为一个充分小的正数，称为收敛精度；Jk为第k次规划时行驶总距离，其中J=规划区域m内充电需求点个数。

若不满足收条件节，则返回步骤3，继续聚类寻找更优充电区域划分和充电站点选址；若满足收敛条件，则每个聚类集合即为划分充电区域，其中央点坐标 (xθm,yθm)为充电站点坐标。

3 算例及性能评价

3.1 实际规划算例

本文以天津市中心城区电动汽车集中型充电站规划为例，规划区域总面积9.98 km2；区域内包含大型商超、医院学校、旅游景点、政企周边及大型居住区等，规划充电需求点265处；各充电需求点和变电站的地理位置由GIS获取，如图2所示。

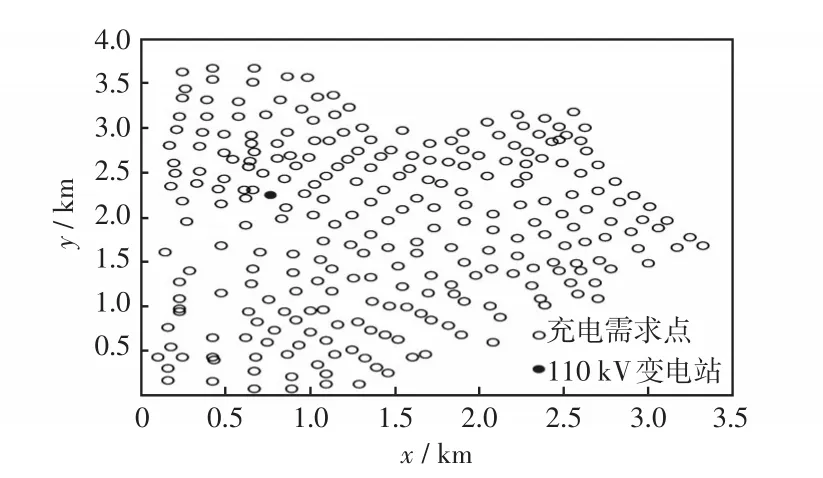
图2 充电需求点及配电网地理位置信息Fig.2 Geographic information of charging demand points and distribution network

依照区域内配电系统现状可提供充电站进线10 kV，型号为JKLYJ-150。区域内人口密度γ3，汽车占有率γ4，道路非直线系数β，泊松参数λ以及充电站投资运营成本等参数见表1。

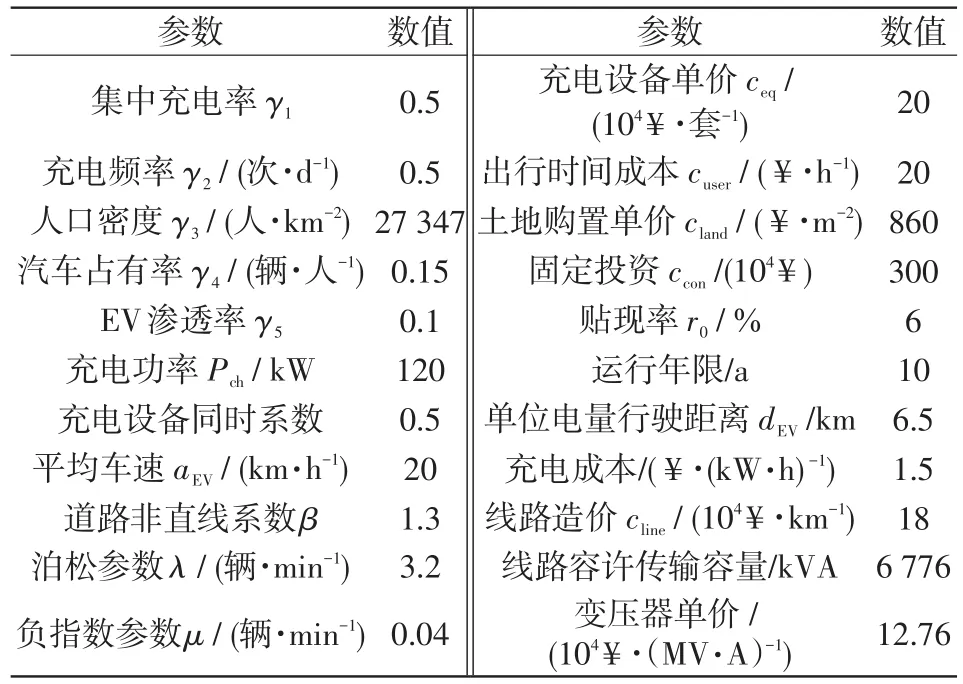
表1 参数设定Tab.1 Setting of parameters

各充电需求点EV充电需求量Q(vi)可表示为

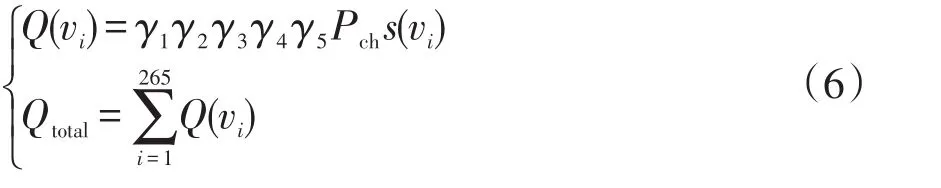
式中：s（vi）为充电需求点vi的面积；Pch为充电功率。

3.2 充电站建设数量计算选择

根据表1数据和式（6），可求得规划区域内EV集中充电需求量Qtotal=22.58 MW，进而利用式（2）计算得出充电站数量上下限为Nch_min=6，Nch_max=24。对[Nch_min,Nch_max]内的待选方案进行线路潮流、电压偏移等约束条件校验，获得当充电站建设数量选择为8、9、11和15座时，满足充电站容量约束，而考虑到充电站建设运营成本以及中心城区的稀奇土地占用等因素，选择较少的8座充电站在保证用户充电需求情况下更有利于成本节约。

3.3 充电区域站定址及服务范围划分算法性能评价

为评测本文所提出的基于图中央点的改进K-means算法的优异性，选取K-means聚类规划算法和Voronoi图计算几何法[13]为对比算法，同样对8站点方案进行服务范围划分和定址计算。

各服务子区域内充电需求点个数统计如图3所示，以及需求点到各自充电站的距离和统计如图4所示。由图3和图4可知，基于图中央点的改进K-means算法进行服务子区域划分更均匀，需求点到各自充电站的距离更短。与之相比单纯K-means算法规划后有62.5%的服务区域充电距离变长。而采用Voronoi图计算几何法规划效果最差，最大区域包含51个充电需求点，而最小区域仅有10个充电需求点。区域内过于拥挤的充电需求将导致用户等待时间拉长，致使顾客流失，而较少的区域又会造成资产利用率不足，且Voronoi图计算几何法规划最大充电距离比基于图中央点的改进K-means算法增加了3.18倍，增加了EV用户充电成本。因此，基于图中央点的改进K-means算法进行的城市集中型充电规划具有更好的经济性。

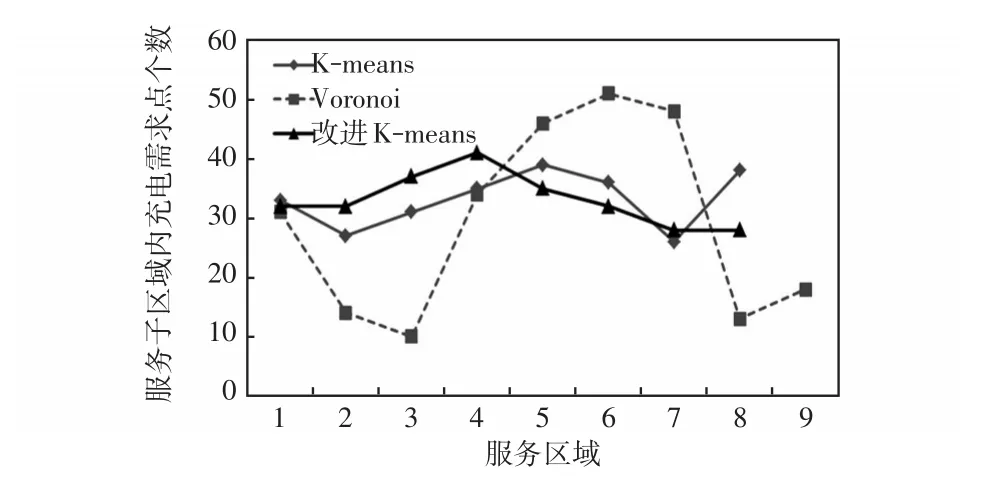
图3 各服务子区域内充电需求点个数统计Fig.3 Statistics of the numbers of charging demand points in each sub service-area

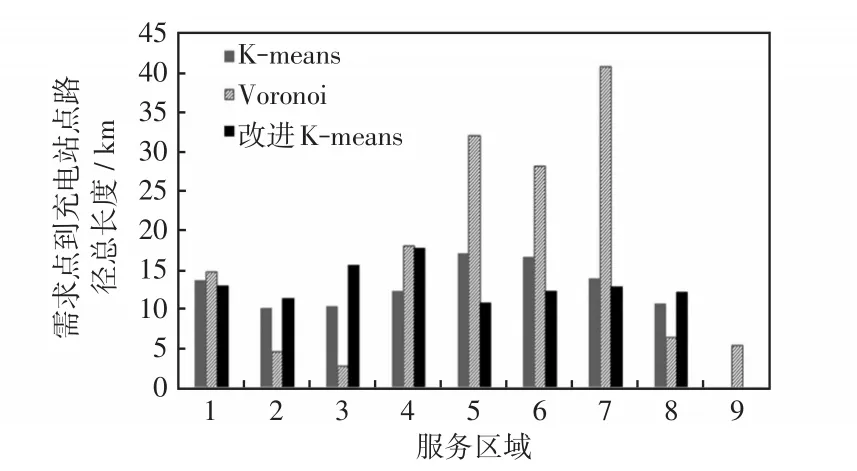
图4 各服务子区域内需求点到各自充电站的距离和统计Fig.4 Statistics of the distances from charging demand points to the respective charging stations in each sub service-area

表2给出不同可行建设方案社会成本计算。

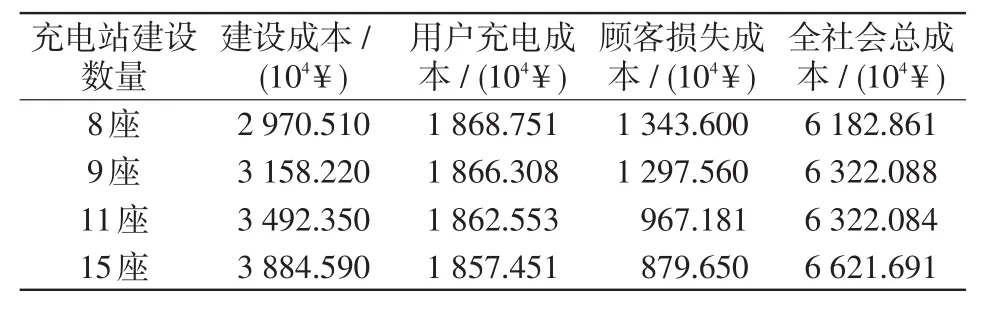
表2 可行建设方案社会成本计算Tab.2 Calculated costs of feasible construction schemes

4 结语

本文针对规划区域内EV的时空分布特点，在考虑交通情况、用户充电成本及配电网约束等多种影响因素基础上，构建了充电站选址的图模型。在考虑规划区域内EV集中充电需求量和单台充电设备容量的基础上，将图论中央点理论与K-means聚类算法相结合提出集中型充电站选址和服务范围划分算法。通过天津中心某城区实际规划算例计算，并与K-means和Voronoi图计算几何法比较判定本文所提方法规划的城市充电站区域划分更均衡，并且具有更小的充电距离。