让学生的思维插上逆向的翅膀

陈文珍

（漳州市新桥中心小学，福建 漳州）

逆向思维也叫求异思维，它是对司空见惯的似乎已成定论的事物或观点反过来思考的一种思维方式。敢于“反其道而思之”，让思维向对立面的方向发展，从问题的相反面深入地进行探索，树立新思想，创立新形象。《义务教育数学课程标准》指出让学生获得分析问题和解决问题的一些基本方法，体验解决问题方法的多样性，发展创新意识。而如何在小学数学课堂中培养学生的逆向思维呢？我认为可以从以下几个方面入手。

一、紧扣教材、深挖教材，潜移默化地培养学生的逆向思维

纵观1～6年级各教学知识点，都有潜在的培养学生逆向思维的教材，例如：

事例一：一年级上册的“分与合”这一课时，教材结合分红花的生活情境出示例题，教师在组织学生分红花的过程中，让学生经历4可以分成1和3；4可以分成2和2；4可以分成3和1时，从而教学了4的分成，此时，教师可引导学生逆向思考，即1朵红花和3朵红花合成4朵。同理引导学生尝试自己归纳出2和2合成4，3和1合成4，从而有意识地培养学生的逆向思维。教材的做一做第一题，也是让学生在猜一猜的活动环节中，让学生经历“因为3分成1和2，所以1和2合成3”这样一个正反思考的过程，从而引导学生敢于“反其道而思之”，潜移默化地培养了学生的逆向思维。

事例二：一年级下册第二单元“20以内的退位减法”的教学，例如：15-9=6的算理可以有两种，一种是先拿十位上的10-9=1，然后所剩的1再和个位上的5相加得6，一种就是培养学生逆向思维的方法即因为6+9=15，所以逆向倒推15-9=6，从而让学生真实地感知减法是加法的逆运算；二年级下册“用2-6的乘法口诀求商”的教学，例如：教学12÷3=？教师引导学生思考3×？=12，根据口诀“三四十二”得知 3×4=12，所以逆向倒推 12÷3=4，同样的让学生真实感知除法是乘法的逆运算，为四年级知识的教学奠定基础，也水到渠成地渗透逆向思维，潜移默化地培养学生的逆向思维。

事例三：二年级上册教材第23面例题4“比多比少”的教学，例如：一班得了12面小红旗，二班比一班多得3面，二班得了多少面？教师带领学生分析条件时，对于“二班比一班多得3面”这个条件的分析，我认为教师可以引导学生逆向思考即“二班比一班多得3面”说明“一班比二班少得3面”，从而培养学生的逆向思维。

事例四：三年级下册的“长方形、正方形面积的计算”第二课时进行练习长方形、正方形面积的计算时。我认为教师可以引导学生根据“长方形面积=长×宽”“正方形面积=边长×边长”，逆向推导出“长方形面积÷长=宽”“长方形面积÷宽=长”等计算公式，从而有效地培养学生的逆向思维。

事例五：四年级上册“角的度量”这一知识点的教学，教师在学生能熟练掌握角的度量时，在进行练习时可以进行逆向思维的训练，例如：度量一个角时，角的一边对着量角器上“180度”的刻度线，另一端对着“50度”的刻度线，这个角是几度？教师出示这样的习题时，先请学生回忆如何正确量出角的度数，学生在回想的过程中，脑海里就会出现跟题目中所提到的“角的一边对着量角器的180度”相反的情形即量角的度数时，“0”刻度线与角的一条边重合，角的一条所对的量角器上的刻度，就是这个角的度数，那么，角的一边不是对着“0”刻度线而是对着“180度”，说明是逆向推导回来，另一边对着“50度”，说明这个角的度数与“180度”相差“50度”，所以，这个角的度数应该是“180度-50度=130度”，相信教师长期引导训练，学生能更全面地掌握知识点，同时也培养了学生的发散思维及逆向思维。

事例六：四年级下册“小数的意义”当学生已经学习了小数的意义时，明确一位小数就是表示把单位“1”平均分成10份，取其中的几份，计数单位是十分之一，写成0.1；两位小数就是表示把把单位“1”平均分成100份，取其中的几份，计数单位是百分之一，写成0.01；三位小数就是表示把把单位“1”平均分成1000份，取其中的几份，计数单位是千分之一，写成0.001……

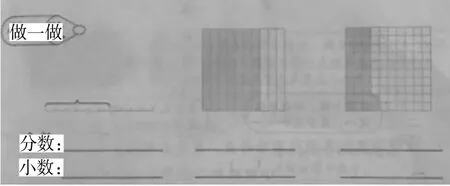
教材第33面《做一做》让学生看图写分数、小数，其目的就是巩固对小数意义的理解，此时，教师可多提出这样一个问题：“第一幅图没取的是几份，用分数、小数怎么表示；第二幅图没涂色的是几份用分数、小数怎么表示；同理第三幅图没涂色的是几份，用分数、小数怎么表示。”这样既能达到巩固知识点的目的，又能培养学生逆向思考问题，从而促进学生逆向思维的发展。

二、结合数学阅读，“润物细无声”地培养学生的逆向思维

通过数学“大阅读”，拓展学生的视野，培育学习兴趣，激发学生思考，改变思维方式，陶冶学生情操。例如，学生阅读“马小跳玩数学”——《粒粒皆辛苦》这篇故事。学生既能感受到生活中的数学，又能体验学习解决问题的方法——抓住有用信息、条件，整合资源，明确解题思路。以上故事问题属于“还原问题”，从结果入手，逆向倒推求出原来的量，阅读这样的数学故事，有助于学生逆向思维的培养。

总之，逆向思维是学生轻松学好数学不可缺少的一种思维方式，教师应用心用力常抓不懈！