FI代数上基于模糊滤子的一致拓扑空间

刘春辉

(赤峰学院 数学与统计学院， 内蒙古 赤峰 024000)

0 引 言

在模糊逻辑的理论与应用研究中，蕴涵连接词“如果…，那么…”起着非常重要的作用. 因此，探讨在模糊逻辑推理中经常使用的蕴涵算子的共同本质是一项十分有意义的工作. 作为对逻辑蕴涵连接词进行代数化处理尝试的成果，吴望名教授[1]提出了Fuzzy蕴涵代数的概念，简称FI代数. 值得注意的是，众多著名的逻辑代数，如MV代数、格蕴涵代数、BL-代数、MTL-代数、R0-代数、剩余格代数以及Heyting代数等都可看作FI代数的特例，因此，对FI代数的研究具有广泛的代表性. 迄今为止，已有学者针对这一代数结构做了大量研究工作，获得了若干具有理论价值和应用前景的成果[2-10].滤子作为一种工具性概念在命题逻辑系统及与之相匹配的语义代数完备性证明中扮演着重要角色. 从逻辑观点来看，各种不同的滤子对应不同的可证公式集. 鉴于此，许多学者从不同的角度对FI代数提出了多种不同形式的滤子概念，并对其性质和模糊化问题进行了深入细致的研究[11-15].

近年来，借助拓扑工具描述逻辑问题越来越受到学术界的关注，为逻辑问题的研究提供了新的方法和途径. 其中，文献[16]在R0-代数上以全体MP滤子为基础建立了拓扑空间并讨论了该空间的若干拓扑性质. 文献[17-18]分别讨论了R0-代数和FI代数的素滤子拓扑性质. 文献[19-20]分别研究了剩余格和FI代数中素模糊滤子的拓扑性质. 文献[21-24]分别在BL代数、R0-代数和FI代数中基于MP滤子诱导的同余关系构造了一致结构和一致拓扑，并研究了相应一致拓扑空间的性质.受上述一系列工作的启发，本文基于由模糊滤子诱导的同余关系在FI-代数上构造一致结构和一致拓扑，讨论一致拓扑空间的拓扑性质及商空间性质，获得了一些有意义的结论.

1 预备知识

定义1[1]若对任意的x,y,z∈X，条件(I1)～(I5)成立，则称(2,0)型代数(X,→,0)为Fuzzy蕴涵代数，简称为FI代数.

(I1)x→(y→z)=y→(x→z)；

(I2) (x→y)→((y→z)→(x→z))=1；

(I3)x→x=1；

(I4)x→y=y→x=1⟹x=y；

(I5) 0→x=1，

其中，1=0→0.

为叙述方便，如无特殊说明，以下总将FI代数(X,→,0)简记为X. 为了讨论FI代数的性质，文献[1]在FI代数X上定义偏序≤满足：

x≤y⟺x→y=1，∀x,y∈X.

引理1[1]设X为FI代数，则∀x,y,z∈X有

(I6)x→1=1，1→x=x；

(I7)x≤y⟹z→x≤z→y,y→z≤x→z；

(I8)x→y≤(z→x)→(z→y)；

(I9) ((x→y)→y)→y=x→y；

(I10)x≤(x→y)→y，y≤(x→y)→y.

定义2[1]设X为FI代数，∅≠F⊆X.若1∈F且∀x∈F，y∈X，x→y∈F⟹y∈F,则称F为X的滤子.

设X是非空集合，X上的一个模糊集是指映射f：X→[0,1]. 对X上的模糊集f和t∈[0,1]，称集合ft={x∈X|f(t)≥t}为f的t-水平子集.设f和g是X上的2个模糊集，{fλ}λ∈Λ是X上的一族模糊集，∀x∈X，定义：

(1) (f∩g)(x)=f(x)∧g(x)；

(2) (f∪g)(x)=f(x)∨g(x)；

(3) (∩λ∈Λfλ)(x)=∧λ∈Λfλ(x)；

(4) (∪λ∈Λfλ)(x)=∨λ∈Λfλ(x).

定义3[13-14]设X为FI代数，f为X上的模糊集，若∀x,y∈X，下列条件成立：

(FF1)f(1)≥f(x)；

(FF2)f(y)≥f(x)∧f(x→y)，

则称f为X的模糊滤子.X的全体模糊滤子构成的集合记为FFil(X).

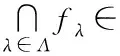
引理2[13-14]设X为FI代数，f∈FFil(X)，则∀x,y,z∈X,下列各结论成立：

(FF3)f(x→y)=f(1)⟹f(x)≤f(y)；

(FF4)x≤y⟹f(x)≤f(y)；

(FF5)f(x→y)∧f(y→z)≤f(x→z)；

(FF6)f(x→y)≤f(y→z)∧f(x→z)；

(FF7)f(x→y)≤f(z→x)∧f(z→y).

定义4[14]设X为FI代数，若R满足：

(1) 自反性、对称性和传递性；

(2) ∀x,y,z∈X，xRy⟹(x→z)R(y→z)且(z→x)R(z→y)，

则称X上的二元关系R⊆X×X是X上的同余关系.

引理3[14]设X为FI代数，f∈FFil(X).定义X上二元关系≡f：X×X→X满足： ∀x,y∈X,

x≡fy⟺f(x→y)=f(y→x)=f(1)，

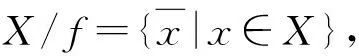
2 基于模糊滤子的一致拓扑空间

设X是一个非空集合，U,V⊆X×X，定义：

(1)U∘V={(x,y)∈X×X|∃z∈X,(x,z)∈V, (z,y)∈U}；

(2)U-1={(x,y)∈X×X|(y,x)∈U}；

(3) Δ={(x,x)∈X×X|x∈X}.

定义5[25-26]设X是非空集合，ω是X×X的非空子集族. 若下列各条件成立：

(U1) ∀U∈ω，Δ⊆U；

(U2) ∀U∈ω，U-1∈ω；

(U3) ∀U∈ω，∃V∈ω，V∘V⊆U；

(U4) ∀U,V∈ω，U∩V∈ω；

(U5)U∈ω且U⊆V⊆X×X，蕴涵V∈ω，

则称ω是X上的一致结构，称(X,ω)是一致空间.

设ω是X上的一致结构，x∈X，U∈ω，记U[x]={y∈X|(x,y)∈U}，则ω可自然诱导拓扑：

τ={O⊆X|∀x∈O,∃U∈ω, s.t.U[x]⊆O}，

称之为X上的一致拓扑，并称(X,τ)为一致拓扑空间.

下面在FI代数上基于模糊滤子构造一致结构和一致拓扑空间. 为此，设X为FI代数，且记∅≠FFil*(X)⊆FFil(X)，满足：

(1) ∀f,g∈FFil*(X)，f(1)=g(1)；

命题1设X为FI代数，∀f∈FFil*(X)，记集合Uf={(x,y)∈X×X|x≡fy}，则X×X的子集族ω*={Uf|f∈FFil*(X)}满足条件(U1)～(U4).

证明首先，由≡f的自反性、对称性和传递性知，ω*满足(U1)～(U3). 其次，任取Uf,Ug∈ω*，则f∩g∈FFil*(X)，从而f(1)=g(1)=(f∩g)(1)，故∀x,y∈X，f(x→y)=f(1)且g(x→y)=g(1)当且仅当(f∩g)(x→y)=(f∩g)(1)，因此可得Uf∩Ug=Uf∩g.再由f∩g∈FFil*(X)，可得Uf∩Ug∈ω*，即ω*亦满足(U4).

定理1设X为FI代数，定义集合

ω={U⊆X×X|∃Uf∈ω*, s.t.Uf⊆U}，

则ω是X上的一致结构，从而(X,ω)是一致空间.

证明由命题1和ω的定义知，ω满足条件(U1)～(U4)，因此只需证明ω满足条件(U5)即可. 事实上，设U∈ω且U⊆V⊆X×X，则存在Uf∈ω*使得Uf⊆U⊆V，故V∈ω.

由定义5和定理1，有

定义6设X为FI代数，则

τ={O⊆X|∀x∈O,∃U∈ω, s.t.U[x]⊆O}

为X上的一个拓扑，称之为X上基于模糊滤子的一致拓扑，并称(X,τ)为X上基于模糊滤子的一致拓扑空间. 特别地，当FFil*(X)={f}时，ω={U⊆X×X|Uf⊆U}，此时记X上基于模糊滤子的一致拓扑τ=τf.

注2设X为FI代数，由定义6中拓扑τ的定义知，∀x∈X及f∈FFil*(X)，Uf[x]均为点x的开邻域.

例1设X={0,a,b,1}，定义X上二元运算“→”如表1所示，则(X,→,0)是一个FI代数. 定义X上模糊集f使f(0)=f(b)=α,f(a)=f(1)=β,0≤α<β≤1，则f∈FFil(X). 令FFil*(X)={f}，则

ω*={Uf|f∈FFil*(X)}=

{{(x,y)∈X×X|x≡fy}}=

{{(0,0),(a,a),(b,b),(1,1),(a,1),(1,a),(0,b),(b,0)}}

从而ω={U⊆X×X|∃Uf∈ω*, s.t.Uf⊆U}是X上的一个一致结构，且Uf[0]=Uf[b]={0,b}，Uf[a]=Uf[1]={a,1}. 因此，X上基于模糊滤子的一致拓扑τ=τf={∅,{0,b},{a,1},X}.

表1 二元运算“→”的定义Table 1 Definition of unary operator “→”

定理2设X为FI代数，若χ{1}∈FFil*(X)，则X上基于模糊滤子的一致拓扑τ是离散拓扑.

证明设f=χ{1}∈FFil*(X)，则∀x∈X，有

于是，由(I4)得

Uf[x]={y∈X|x≡fy}=

{y∈X|f(x→y)=f(y→x)=f(1)=1}=

{y∈X|x→y=y→x=1}=

{y∈X|y=x}={x}，

故{x}=Uf[x]∈τ，即(X,τ)中任意单点集都是开集，因此τ是离散拓扑.

注3定理2的逆命题一般不真. 例如，设X为例1中所给的FI代数，在X上定义模糊集g，使得

g(0)=g(a)=α，g(b)=β，g(1)=γ，

0≤α<β<γ≤1，则可验证g∈FFil(X). 令FFil*(X)={g}，则

ω*={Uf|f∈FFil*(X)}=

{{(x,y)∈X×X|x≡gy}}=

{{(0,0),(a,a),(b,b),(1,1)}}，

于是Ug[x]={x},∀x∈X，τ=τg是离散拓扑. 显然χ{1}∉FFil*(X).

下面讨论FI代数X上基于模糊滤子的一致拓扑空间(X,τ)的拓扑性质.

定理3设X为FI代数，则对任意的x∈X及f∈FFil*(X)，都有Uf[x]是一致拓扑空间(X,τ)中的既开又闭集.

证明任取x∈X和f∈FFil*(X)，首先，由注2知，Uf[x]是(X,τ)中的开集. 其次，证明Uf[x]为(X,τ)中的闭集.只须证对任意的x∈X，(Uf[x])c∈τ. 为此，假设y∈(Uf[x])c，断言Uf[y]⊆(Uf[x])c. 事实上，任取z∈Uf[y]，则y≡fz，从而f(y→z) =f(z→y)=f(1).若z∉(Uf[x])c，则z∈Uf[x], 从而x≡fz，进而f(x→z)=f(z→x)=f(1). 于是由(FF5)及f∈FFil(X)得

f(1)=f(y→z)∧f(z→x)≤f(y→x)，

f(1)=f(x→z)∧f(z→y)≤f(x→y)，

故由(FF1)得f(x→y)=f(y→x)=f(1)，从而x≡fy，进而y∈Uf[x]，这与y∈(Uf[x])c矛盾！所以z∈(Uf[x])c，因此Uf[y]⊆(Uf[x])c.表明(Uf[x])c∈τ，从而Uf[x]也是(X,τ)中的闭集.

引理4[25]拓扑空间(X,T)是非连通的当且仅当X有既开又闭的非空真子集.

推论1设X为FI代数，则X上的基于模糊滤子的一致拓扑空间(X,τ)是非连通空间.

证明由定理3和引理4立即证得.

定理4设X为FI代数，F⊆X是X的滤子且χF∈FFil*(X)，则F是一致拓扑空间(X,τ)中的既开又闭集.

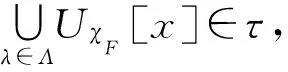
注4定理4的逆命题一般不真. 即当F是X的滤子且为一致拓扑空间(X,τ)中的既开又闭集时，不必有χF∈FFil*(X). 例如，考虑例1中所给一致拓扑空间(X,τ)，则F={a,1}是FI代数X的滤子，且由定理3知，F={a,1}=Uf[a]是(X,τ)中的既开又闭集，但由

知，χF≠f，从而χF∉FFil*(X).

命题2设X为FI代数，f,g∈FFil(X)，f(1)=g(1)且f⊆g，即f(x)≤g(x),∀x∈X，则Uf⊆Ug.

证明设f,g∈FFil(X)，f(1)=g(1)且f⊆g. 任取(x,y)∈Uf，则

g(1)=f(1)=f(x→y)≤g(x→y)，

g(1)=f(1)=f(y→x)≤g(y→x)，

而由g∈FFil(X)及(FF1)可得g(1)≥g(x→y)，且g(1)≥g(y→x)，故g(x→y)=g(y→x)=g(1), 从而有(x,y)∈Ug，因此Uf⊆Ug.

定理5设X为FI代数，f,g∈FFil(X)，f(1)=g(1)且g⊆f，则τf⊆τg.

证明由定义6，令

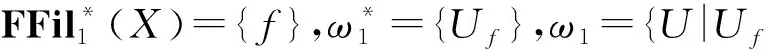
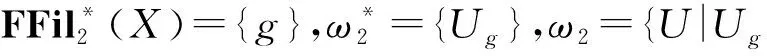
任取O∈τf，则∀x∈O，∃U∈ω1使得U[x]⊆O，从而Uf[x]⊆U[x]⊆O. 又g⊆f，所以由命题2得Ug⊆Uf，故Ug[x]⊆Uf[x]⊆U[x]⊆O，因此O∈τg，表明τf⊆τg.

注5定理5的逆命题一般不成立. 例如，设X={0,a,b,c,1}，定义X上二元运算“→”如表2所示，则(X,→,0)是一个FI代数. 定义X上的2个模糊集f和g满足：

f(0)=f(a)=0.3，f(b)=f(c)=f(1)=0.8，

g(0)=g(a)=0.5，f(b)=0.6,f(c)=f(1)=0.8,

则f,g∈FFil(X)且f(1)=g(1).

令FFil*(X)={f}，可得

τf={∅,{0,a},{b,c,1},X}.

令FFil*(X)={g}，可得

τg={∅,{0},{a},{b},{c,1},{0,a},{0,b},{a,b}, {0,a,b},{0,c,1},{a,c,1},{b,c,1},{0,b,c,1}, {a,b,c,1},{0,a,c,1},X}.

则τf⊆τg，但g⊆f显然不成立.

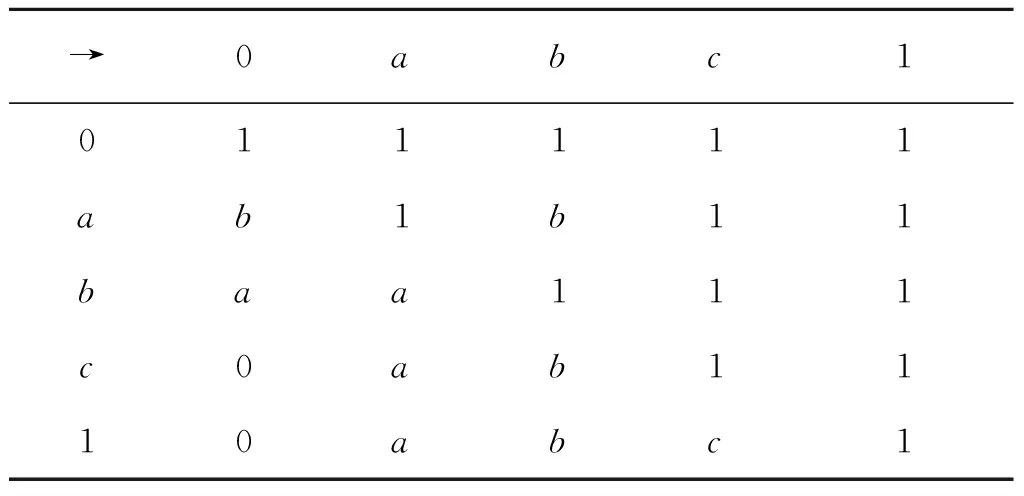
表2 二元运算“→”的定义Table 2 Definition of unary operator “→”

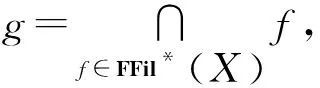
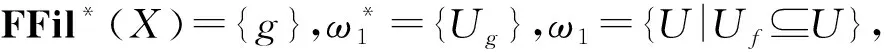
为了讨论基于模糊滤子的一致拓扑空间的紧致性，首先引用如下定义：

定义7[25-26]设(X,T)是拓扑空间且A⊆X，若A的任一开覆盖都有有限子覆盖，则称A是X的紧子集. 若X本身为紧子集，则称(X,T)为紧空间.若x∈X有紧邻域，则称X在点x处是局部紧的. 若X在其中每一点处都是局部紧的，则称(X,T)为局部紧空间.

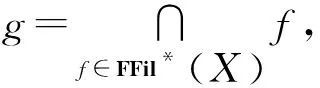
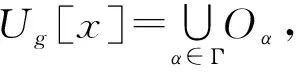
推论2设X为FI代数，则X上基于模糊滤子的一致拓扑空间(X,τ)是局部紧空间.

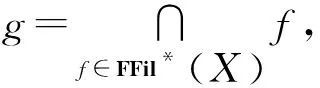
引理5[25]若(X,ω)是一致空间，则一致拓扑空间是完全正则空间.

推论3设X为FI代数，则X上基于模糊滤子的一致拓扑空间(X,τ)是完全正则空间.

总结推论1～推论3,立得以下定理：

定理8设X为FI代数，则X上基于模糊滤子的一致拓扑空间(X,τ)是非连通、局部紧的完全正则空间.

定理9设X为FI代数，f∈FFil(X)，则下列陈述等价：

(1) 一致拓扑空间(X,τf)是紧空间；

(2) 一致空间(X,ω)是全有界的；

证明(1)⟹(2)： 由文献[25]第6章定理32可立得.

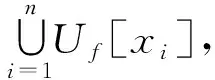
关于基于模糊滤子的一致拓扑空间的分离性，有以下结论：

定理10设X为FI代数，则下列陈述等价：

(1) 一致拓扑空间(X,τ)是T0空间；

(2) 一致拓扑空间(X,τ)是T1空间；

(3) 一致拓扑空间(X,τ)是T2空间.

证明(1)⟹(2)： 设(X,τ)是T0空间且x,y∈X使得x≠y，则由(I4)得x→y≠1或y→x≠1. 不妨设x→y≠1，则由(X,τ)是T0空间知，存在O∈τ使得x→y∈O且1∉O，从而存在f∈FFil*(X)使得Uf[x→y]⊆O. 由假设，显然有1∉Uf[x→y]且x→y∉Uf[1]，故(X,τ)是T1空间.

(2)⟹(3)： 设(X,τ)是T1空间且x,y∈X使x≠y，则存在O1,O2∈τ使得x∈O1，y∉O1且y∈O2，x∉O2，所以存在f,g∈FFil*(X)使得Uf[x]⊆O1且Ug[x]⊆O2. 记h=f∩g，则由注1得h∈FFil*(X)，往证Uh[x]∩Uh[y]=∅. 事实上，设z∈Uh[x]∩Uh[y]，则h(z→x)=h(x→z)h(z→y)=h(y→z)=h(1)，从而由(FF5)得

h(1)=h(x→z)∧h(z→y)≤h(x→y)，

h(1)=h(y→z)∧h(z→x)≤h(y→x)，

故由(FF1)得h(x→y)=h(y→x)=h(1)，于是由h⊆f得y∈Uh[x]⊆Uf[x]⊆O1，这与y∉O1矛盾！因此(X,τ)是T2空间.

(3)⟹(1)： 显然.

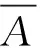
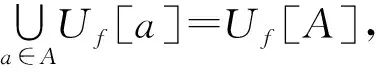
从而b∈∩{Uf[A]|Uf∈ω*}.

定理12设X是FI代数，C为X上基于模糊滤子的一致拓扑空间(X,τ)的紧子集，O∈τ且C⊆O，则∃f∈FFil*(X)使得C⊆Uf[C]⊆O.

最后，讨论FI代数中蕴涵算子关于一致拓扑的连续性.

定义10设(X,→,0)是FI代数，T是X上的拓扑，若运算“→”关于拓扑T连续，则称(X,T)是拓扑FI代数.

注6设(X,→,0)是FI代数，T是X上的拓扑，A,B⊆X，定义

A→B： ={a→b∈X|a∈A,b∈B}，

则运算“→”关于拓扑T连续等价于∀O∈T，∀a,b∈X，当a→b∈O时，存在O1,O2∈T使得a∈O1，b∈O2且O1→O2⊆O.

定理13设(X,→,0)是FI代数，τ是X上基于模糊滤子的一致拓扑，则(X,τ)是拓扑FI代数.

证明任取a,b∈X，O∈τ，设a→b∈O，则由τ的定义知，存在U∈ω使U[a→b]⊆O，且存在f∈FFil*(X)使Uf⊆U，于是可断言：

Uf[a]→Uf[b]⊆Uf[a→b].

事实上，设x→y∈Uf[a]→Uf[b]，则x∈Uf[a]且y∈Uf[b]，从而x≡fa且y≡fb，故由≡f为X上的同余关系得(a→b)≡f(x→y)，则(a→b,x→y)∈Uf⊆U，故x→y∈Uf[a→b]. 又由Uf⊆U得Uf[a→b]⊆U[a→b]，故令O1=Uf[a]且O2∈Uf[b]，则由注2知，O1,O2∈τ，a∈O1，b∈O2且O1→O2=Uf[a]→Uf[b]⊆Uf[a→b]⊆O. 因此(X,τ)是拓扑FI代数.

3 商空间

本节总假设(X,τ)是拓扑FI代数，且τ为X上基于模糊滤子的一致拓扑.

定义11[25]设X为FI代数，f∈FFil(X)，称按引理3中方式定义的商FI代数X/f上使得投影p：X→X/f为连续开映射的最大拓扑τ*为X/f上的商拓扑，并称(X/f,τ*)为商空间.

注7设X为FI代数，f∈FFil(X)，则在FI代数(X/f,,中，⟺f(x→y)=f(1), ∀

定理14设X是FI代数，且τ为X上基于模糊滤子的一致拓扑，f∈FFil(X)，则商空间(X/f,τ*)是Hausdorff空间.

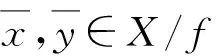
定理15设X是FI代数，且τ为X上基于模糊滤子的一致拓扑，f∈FFil(X)，则商空间(X/f,τ*)是局部紧空间.

引理6[25]任一局部紧的Hausdorff空间都是正则空间.

推论4设X是FI代数，且τ为X上基于模糊滤子的一致拓扑，f∈FFil(X)，则商空间(X/f,τ*)是正则空间.

证明由定理14、定理15和引理6立得.

定理16设X是FI代数，且τ为X上基于模糊滤子的一致拓扑，f∈FFil(X)，则对任意的t∈[0,1]，ft是一致拓扑空间(X,τf)中的闭集.

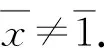
定理17设X是FI代数，且τ为X上基于模糊滤子的一致拓扑，f∈FFil(X)，且商空间(X/f,τ*)是离散空间，则对任意的t∈[0,1]，ft是一致拓扑空间(X,τf)中的开集.

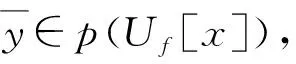
4 结论与展望

将拓扑学概念和原理应用于FI代数问题的研究，基于模糊滤子诱导的同余关系在FI代数上构造了一致结构和一致拓扑，详细讨论了这类空间的拓扑性质，获得了一些有意义的结论. 不但丰富和完善了FI代数理论的研究内容，而且为运用拓扑学工具描述逻辑问题提供了技术支持，进一步促进了拓扑学与模糊逻辑理论的交叉渗透.