P3中的共形极小曲面的构造*
张文娟,陈晓东
(中国科学院大学数学科学学院, 北京 100049) (2017年3月13日收稿; 2017年4月17日收修改稿)
极小曲面的研究一直是微分几何子流形研究领域中的一个重点, 通常对于极小曲面的研究, 会选取具有特殊性质的外围空间, 如空间形式、齐性空间等。而四元数射影空间是对称空间, 因此四元数射影空间中极小曲面的研究具有重要意义。但是因为四元数射影空间本身的结构比较复杂,所以四元数射影空间中极小曲面的研究也颇为困难。
这些年来,在国内外学者的研究下,四元数射影空间中极小曲面的研究也取得了一些重要的研究成果。
1 预备知识
i2=j2=k2=-1,ij=k=-ji,
jk=i=-kj,ki=j=-ik.
可以验证该乘法与上述环运算是等价的。
辛群Sp(n)={A∈GL(n;)|A*T·A=In},其中In表示n阶单位矩阵。对于A∈Sp(n+1),[v]∈Pn,n+1阶辛群Sp(n+1)在Pn上有一个自然的作用:
A·[v]=[Av],
可以验证该作用是可迁的,并且G0=Sp(1)×Sp(n)是该作用在[(1,0,…,0)T]∈Pn处的迷向群。因此,Pn的齐性表示为
Pn=Sp(n+1)/Sp(1)×Sp(n).
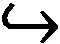

其中π:P2n+1→n+1,是扭映射,它是一个纤维化。
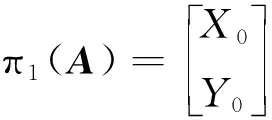
定义1.1由于扭映射是一个纤维化,因此P2n+1上的水平分布H定义为纤维切空间的正交补部分,其中P2n+1上的度量为Fubini-Study度量。特别的,当M是一个黎曼面的时候,如果f:M→P2n+1的切映射的像在H中,则称f为水平曲面。
根据文献[1],对于[z]∈P2n+1,记那么有下述等同:
H[z]↔{w∈z⊥|σz(w)=0,σz=
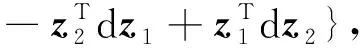
(1)
其中z1,z2∈n+1.
2 P3中的共形极小曲面
在本节中,利用扭映射π:P7→P3来构造P3中的共形极小曲面.
2.1 P2n+1中曲面水平的等价条件
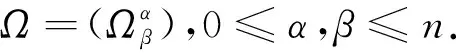
g=g0⊕m,
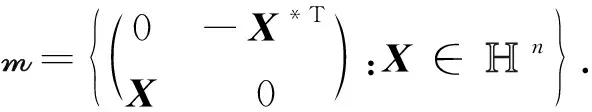
因此,
是m上的一个不变的内积,那么根据齐性空间中不变度量的结论[8],它给出了Pn上的一个不变度量:
(2)
其中ω=s*Ω,s:U⊂Pn→Sp(n+1)为任意一个局部截面。在该不变度量下,辛群Sp(n+1)是Pn的等距群。
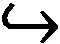
(3)
取g=X+jY∈Sp(n+1),则
Ω=g-1dg,
(4)
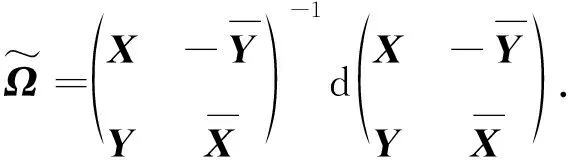
(5)
则式(4)和式(5)可以写成(为书写方便,本文仅给出n=3的情形,一般的情况只是矩阵的维数不同,并没有本质区别):
(6)

(7)
定理2.1设Φ:M→P2n+1是一个浸入,则Φ水平当且仅当其中e:U⊂M→Sp(n+1)是沿Φ的活动标架。
证明取e:U⊂M→Sp(n+1)是沿Φ的活动标架,则π1∘e=Φ,其中π1:Sp(n+1)→P2n+1为自然投影。根据预备知识中的交换图,有π2=π∘π1,所以
π2∘e=π∘π1∘e=π∘Φ,
即e:U⊂M→Sp(n+1)也是一个沿π∘Φ:M→Pn的活动标架。
由式(2),式(3),式(6)和式(7),有
其中γ=e*Γ,σ=e*Σ.
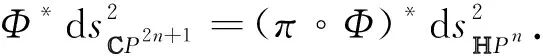
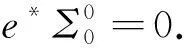
□
定理2.1是从度量的角度来刻画曲面水平的条件的,它与预备知识中的式(1)是从两个不同角度说明曲面水平,它们是等价的.
2.2 P7中的水平全纯曲面
接下来考虑Φ:M→P7是一个水平极小浸入,其中M是一个黎曼面。
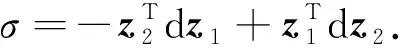
情形1:Φ(M)∩U0≠∅.
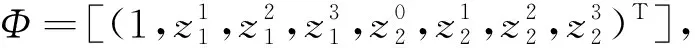
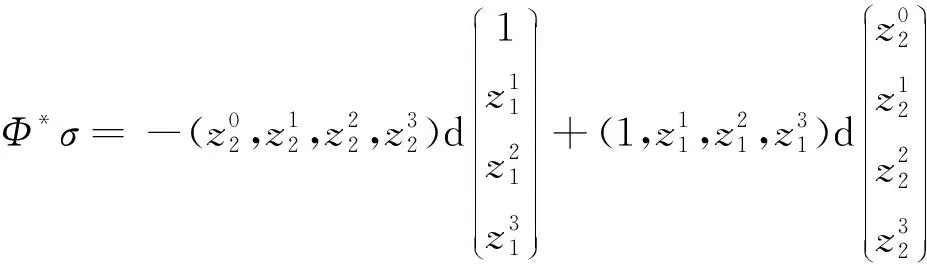
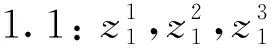
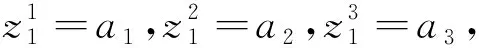
Φ=[(1,a1,a2,a3,a4-a1g1-a2g2-
a3g3,g1,g2,g3)T].
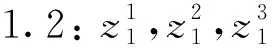
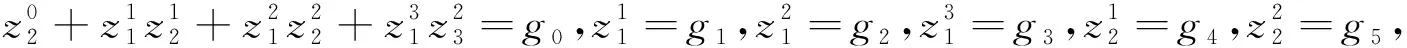
Φ=[(1,g1,g2,g3,g0-g1g4-g2g5-
特别的,此时g1,g2,g4和g5可以取常数.
情形2:Φ(M)∩U0=∅,Φ(M)∩U1≠∅
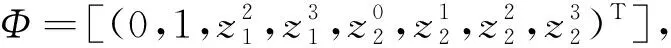
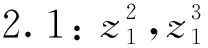
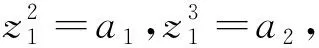
Φ=[(0,1,a1,a2,g1,a3-a1g2-a2g3,g2,g3)T].
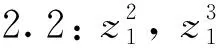
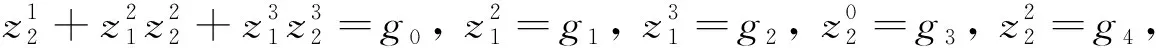
Φ=[(0,1,g1,g2,g3,g0-g1g4-
特别的, 此时g1,g3和g4可以取常数.
情形3:Φ(M)∩(U0∪U1)=∅,Φ(M)∩U2≠∅
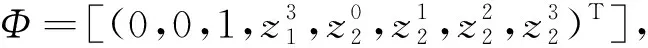
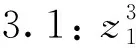
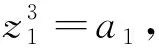
Φ=[(0,0,1,a1,g1,g2,a2-a1g3,g3)T].
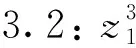
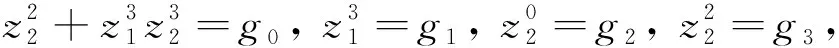
特别的, 此时g1,g3和g4可以取常数.
情形4:Φ(M)∩(U0∪U1∪U2)=∅,Φ(M)∩U3≠∅
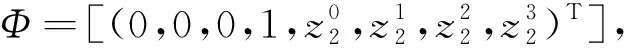
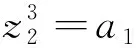
Φ=[(0,0,0,1,g1,g2,g3,a1)T].
情形5:Φ(M)∩(U0∪U1∪U2∪U3)=∅,Φ(M)∩U4≠∅
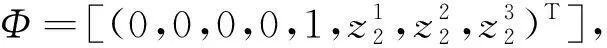
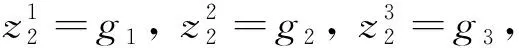
Φ=[(0,0,0,0,1,g1,g2,g3)T].
情形6:Φ(M)∩(U0∪U1∪U2∪U3∪U4)=∅,Φ(M)∩U5≠∅
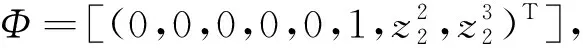
Φ=[(0,0,0,0,0,1,g1,g2)T].
情形7:Φ(M)∩(U0∪U1∪U2∪U3∪U4∪U5)=∅,Φ(M)∩U6≠∅
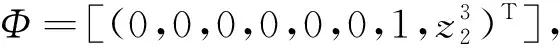
Φ=[(0,0,0,0,0,0,1,g1)T].
情形8:Φ(M)∩(U0∪U1∪U2∪U3∪U4∪U5∪U6)=∅,Φ(M)∩U7≠∅
此时Φ=[(0,0,0,0,0,0,0,1)T]退化, 这与Φ是浸入矛盾。
定理2.2假设Φ:M→P7为水平全纯曲面, 则在相差一个置换矩阵作用的意义下, 局部上Φ一定可以写成下列形式之一:
1)Φ=[(1,a1,a2,a3,a4-a1g1-a2g2-a3g3,g1,g2,g3)T];
3)Φ=[(0,1,a1,a2,g1,a3-a1g2-a2g3,g2,g3)T];
5)Φ=[(0,0,1,a1,g1,g2,a2-a1g3,g3)T];
7)Φ=[(0,0,0,1,g1,g2,g3,a1)T];
8)Φ=[(0,0,0,0,1,g1,g2,g3)T];
9)Φ=[(0,0,0,0,0,1,g1,g2)T];
10)Φ=[(0,0,0,0,0,0,1,g1)T].
其中gm为M上的亚纯函数,an为常数, 其中m=0,…,5,n=1,…,4.
通过简单的直接计算可以验证定理2.2中所给出的10族共形极小曲面满足定理2.1中的条件。所以, 对于P7中水平全纯曲面的构造可以采用定理2.1和式(1)中两种方式, 二者是等价的。
2.3 P3中的共形极小曲面
首先,介绍Eells和Wood的一个结论[9]。
引理2.1设M,Y,N为黎曼流形,π:Y→N为黎曼淹没,f:M→Y是关于映射π的一个水平浸入,如果f调和,则π∘f:M→N也调和。
由于对于共形映射来说, 映射调和等价于映射极小[5], 而P7中的全纯曲面是P7中的Kaehler子流形, Kaehler子流形一定是极小的, 因此, 有
命题2.1设Φ:M→P2n+1是一个水平全纯曲面, 则π∘Φ:M→Pn是共形极小的, 其中π:P2n+1→Pn为扭映射。
例1设gm为黎曼面M上的亚纯函数,an为常数,m=0,…,5,n=1,…,4, 那么有P3中的10族共形极小曲面如下:
M→P3;

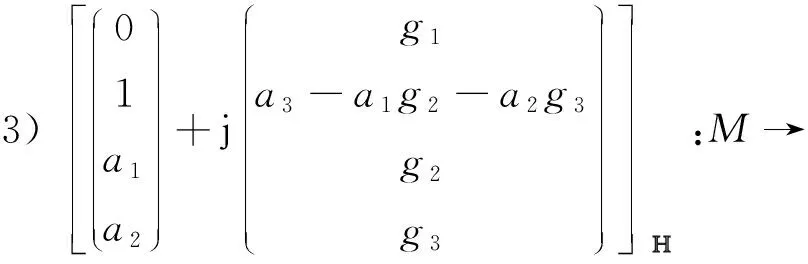
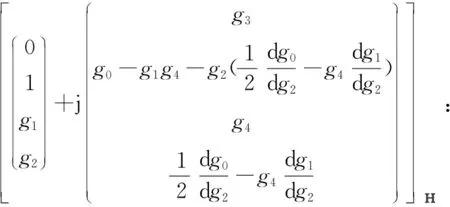
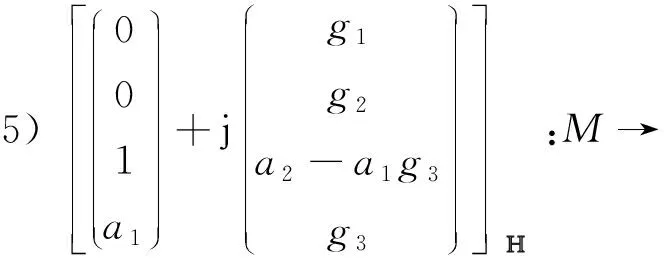

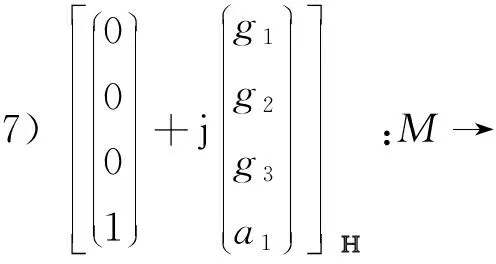
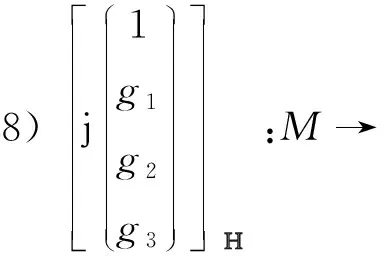
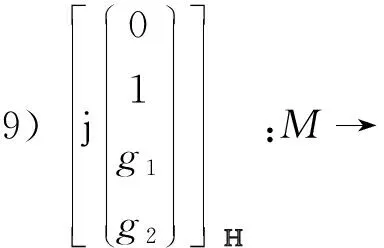
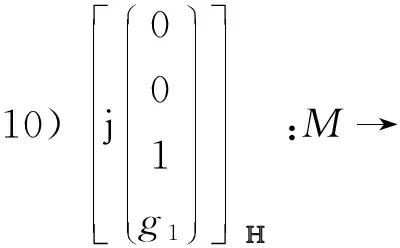
在上述例子中, 可以选取不同形式的亚纯函数及常数, 因此上面的10个例子非常丰富。 而P3中极小曲面的分类依旧是一个很具有挑战性的研究课题, 需要解决的问题还很多。

