怎样学好“循环小数”
循环小数是小数中的一种,其概念较多,容易混淆,那怎样学好“循环小数”呢?
一、先要弄清循环小数与无限小数的区别和联系
小数按照小数部分的位数多少,可以分为有限小数和无限小数。当一个无限小数的小数部分一个数字或几个数字依次不断地重复出现,这样的小数叫作循环小数,因此循环小数一定是无限小数,但无限小数不一定都是循环小数。例如,9.567567567……中的小数部分是567、567、567……三组数字相同,重复出现,所以9.567567567……是循环小数;6.070070007……是无限小数,但小数部分出现的是07、007、0007……分别是两位、三位、四位,不是同一组数依次不断地重复出现,因此6.070070007……就不是循环小数,只是无限不循环小数。还有的学生会把整数部分与小数部分放在一起看或者只看整数部分,认为像33333.12345……这样的小数就是循环小数。它的整数部分虽然都是3,但小数部分数字不同,所以33333.12345……也不是循环小数。它们之间的关系是:
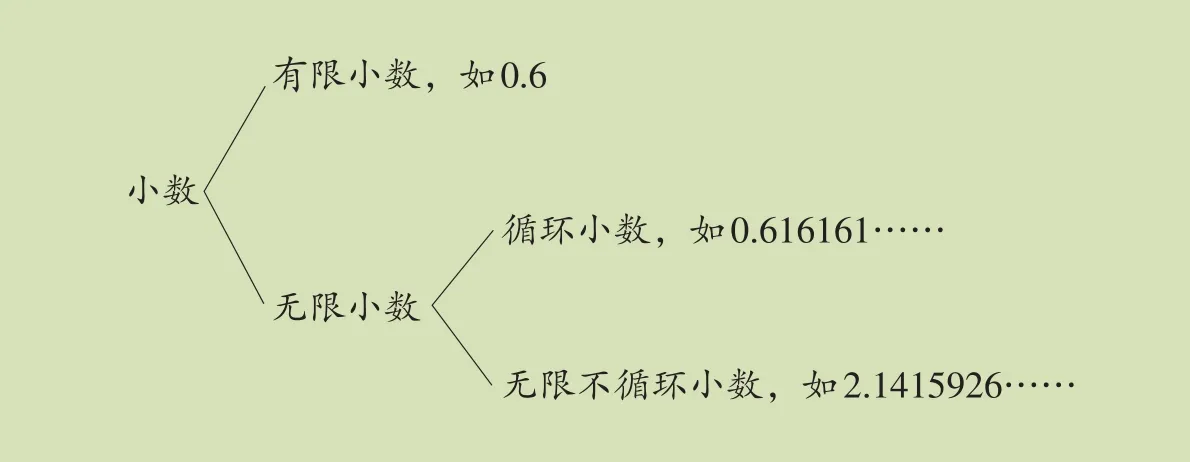
二、其次要区别纯循环小数和混循环小数
从小数部分的第一位起就开始循环的小数叫作纯循环小数;不是从小数部分第一位开始循环的小数叫作混循环小数。如2.616161……是纯循环小数,2.34615615615……就是混循环小数。
其小数部分中依次不断重复出现的数叫作循环节。例如2.616161……中61不断重复出现,所以61是这个循环小数的循环节;2.34615615615……的循环节是615。为了书写方便,我们只要在第一个循环节的首位和末尾数字上面分别点上圆点即可,上面两个循环小数可以写作分别读作二点六一、六一循环和二点三四六一五、六一五循环。
三、最后要掌握循环小数和分数之间的互化
把纯循环小数化成分数,循环节有几位,化成分数的分母就是几位9,分子就是小数部分的循环节。如把混循环小数化成分数,循环节有几位,化成分数的分母就有几位9,小数部分不循环的数有几位,9的后面就添上几个0,分子是第一个循环节及前面的小数部分组成的数,减去不循环数字组成的数。如能约分的通常要约成最简分数。

