一类含参数非线性三阶两点边值问题正解的存在性

武 晨

（江苏联合职业技术学院 南京分院，江苏 南京 210019）

三阶微分方程边值问题在物理学和应用数学等各种不同领域有着广泛的应用，它可以用来描挠度弯曲的梁、电磁波的传播和重力驱动等。由于其广泛的物理背景和现实意义，三阶边值问题引起了许多学者的关注，同时也取得了较多结果，见文献[1-12]。在文献[3]中，作者考虑了三阶三点边值问题：

其中λ＞0。作者通过应用不动点定理得到上述边值问题正解的存在性情况。在文献[4]中，作者考虑了一类三阶两点边值问题：

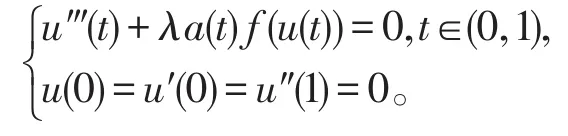
应用锥上的不动点定理得到上述边值问题正解的存在性和多解性条件。

受以上文献的启发，本文研究如下一类三阶两点边值

解的存在性，其中λ＞0。

本文假设以下条件成立

(C1):f:[0,+∞)→[0,+∞):连续;

1 相关引理和定义

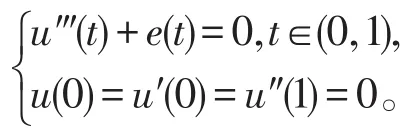
引理2[4]G(t,s)具有如下性质：对于任意的(t,s)∈[0,1]×[0,1]，有

为了得到更好的结果，对于任意0＜τ＜1，定义锥：

定义算子

或者

2 主要结果

定理1假设(C1)、(C2)成立，如果f∞=∞ 或者f0=∞，那么当λ充分小时，边值问题（1）至少存在一个正解。

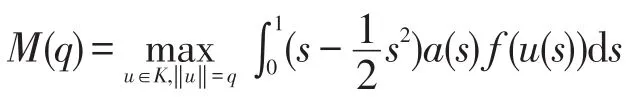
所以，

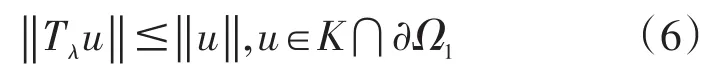
从而

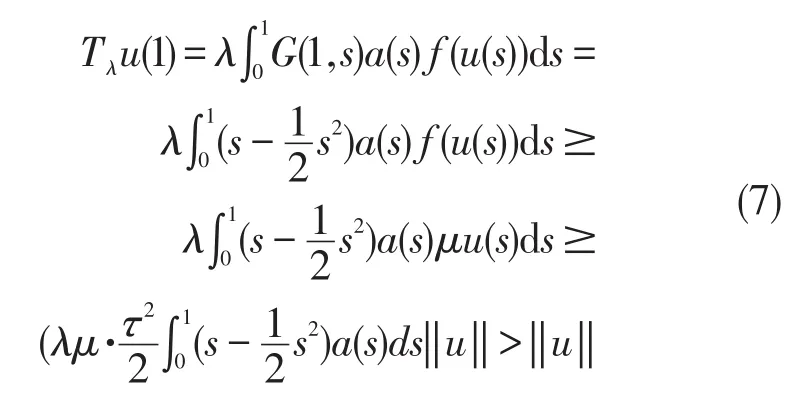
所以，

因此，由（6）（8）和（6）（9）以及引理 5可知，Tλ在和中有不动点，此不动点就是边值问题（1）的正解。

由定理1易得如下的推论：

推论1假设(C1)、(C2)成立，如果f∞=f0=∞，那么当λ充分小时，边值问题（1）至少存在两个正解。

定理2假设(C1)、(C2)成立，如果f∞＜∞且f0＜∞，那么当λ充分小时，边值问题（1）无解。

证明由(C1)可知f是连续的，又因为f∞＜∞ ，f0＜∞ ，从而存在常数M＞0 ，使得f(u)≤Mu成立，其中u∈[0,+∞)。

3 小结

锥拉伸压缩不动点定理作为基本工具，在解决三阶常微分边值问题的时候有重要的应用。通过选择合适的锥，建立适当的格林函数，定义相对应的格林函数算子，对一个含参数非线性三阶两点边值问题解的存在性进行了探讨，最后给出解不存在的一个充分条件，得到了一些新的理论结果，进一步丰富了锥拉伸压缩不动点定理的理论分析和实际应用。