一类银行货币存贮网络模型的系统风险

徐汉亭，李志民

（安徽工程大学 数理学院，安徽 芜湖 241000）

银行业是金融业的主体，在一国的社会经济生活中具有非常重要的地位，也关系到广大的民众。在金融机构联系日益紧密的今天，银行间借贷市场已经成为银行融资的主要来源。在传统的银行业，银行因其特有的业务特点，形成成了一种非常复杂的风险共担网络结构。2008年金融危机的爆发使得人们认识到一方面网络结构在抵御金融风险方面正扮演着非常重要的角色，另一方面也可能导致冲击在网络中传染形成系统性风险。这就使得越来越多的学者致力于金融网络和系统风险这一热点领域的研究。Ichiba等建立了相互作用的Feller扩散系统，研究了系统的稳定性，并且通过相互作用的粒子系统方法估计了多重违约的概率[1]。Carmona等提出了一个简单的银行间借贷和贷款的模型[2]，在模型中N家银行的货币储备是通过扩散过程来描述的，并且在这个模型中证明了央行充当清算机构，只在系统中增加流动性，而不增加其系统性风险。Gai等提出了一种具有任意结构的金融网络中传染的分析模型[3]，研究了危机蔓延的可能性和潜在影响是如何受到聚合和特殊冲击、网络结构变化和资产市场流动性的影响的。Bo等提出了银行间借贷和借贷活动的平均场模型，并将跳过程引入到模型，利用弱收敛分析，得到了与大型银行系统相关联的测度值过程的显式描述，利用极限测度值过程来构建大数定律（LLN）方法近似的系统指标，评估了平均违约距离的情况，并度量了银行间活动的总规模[4]。吴吉林等针对我国短期利率市场的特点，构建了跳跃-扩散-机制转换模型[5]，通过对银行间7天同业拆借利率波动、跳跃和结构变化三种效应的实证分析，证明了该模型具有较好的表现。王宗尧等通过对真实银行间借贷行为的数学抽象，建立了一个动态的银行间借贷网络模型[6]，并利用计算机技术仿真了银行间市场能够展现出的银行间资金流动等诸多规律。

本文在文献[4]的基础上，将模型拓展为由分数布朗运动驱动的相互作用的跳跃-扩散模型，并应用平均违约距离（average distance to default，ADD）指标来刻画银行系统风险，并进行数值模拟。

1 银行货币存贮网络的分数跳扩散模型

考虑系统由K家银行组成，K∈N，给定概率空间 (Ω,F,P)，假设对于第k家银行，k∈{1,2,…,K},其货币储备满足如下的随机微分方程

定理1在满足（3）的条件下，方程（1）存在唯一的非负强解。

证明首先证明不带跳的情形下，在没有跳的情况，（1）式可以改写为下式

令

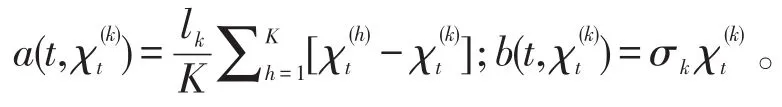
由文献[7]，要证明（4）是存在唯一的非负强解，只需证明存在一个常数M＞0，使得

即要证明下式成立

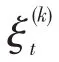
2 系统风险指标

ADD作为一个重要的系统风险度量指标，被广泛地应用。Saldias曾基于2002年第三季度到2011年第一季度的STOXX欧洲600指数，使用该指标对欧洲银行系统的风险进行理论的评估和实证工作[8]。

定义1ADD定义为如下形式

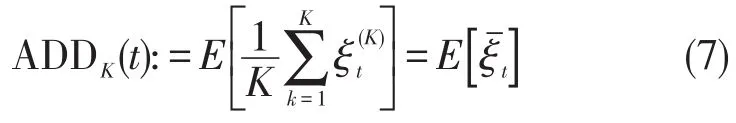
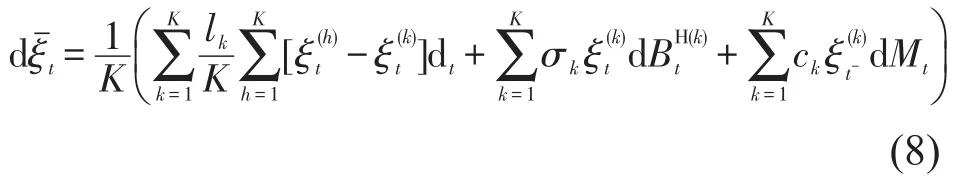
定理2随机微分方程（8）式存在显示解，其解可表示为

由于X是连续过程，J是纯跳过程，故。于是有

微分形式为

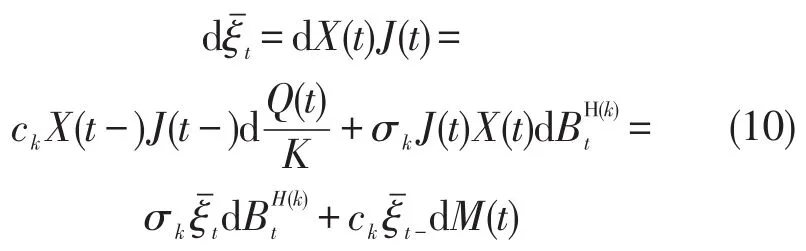
定理得证。

3 数值模拟

由定义1可知

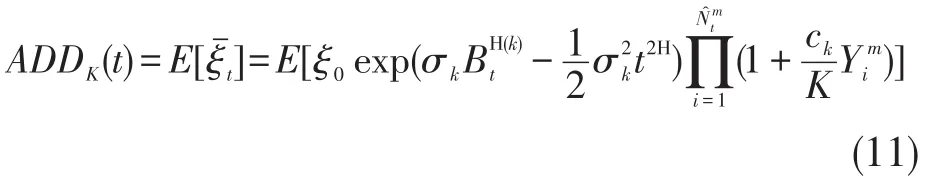
令（11）式中的参数σk，，ck按照以下单调递减的方式收敛到其极限

图1 ADD与H之间的关系

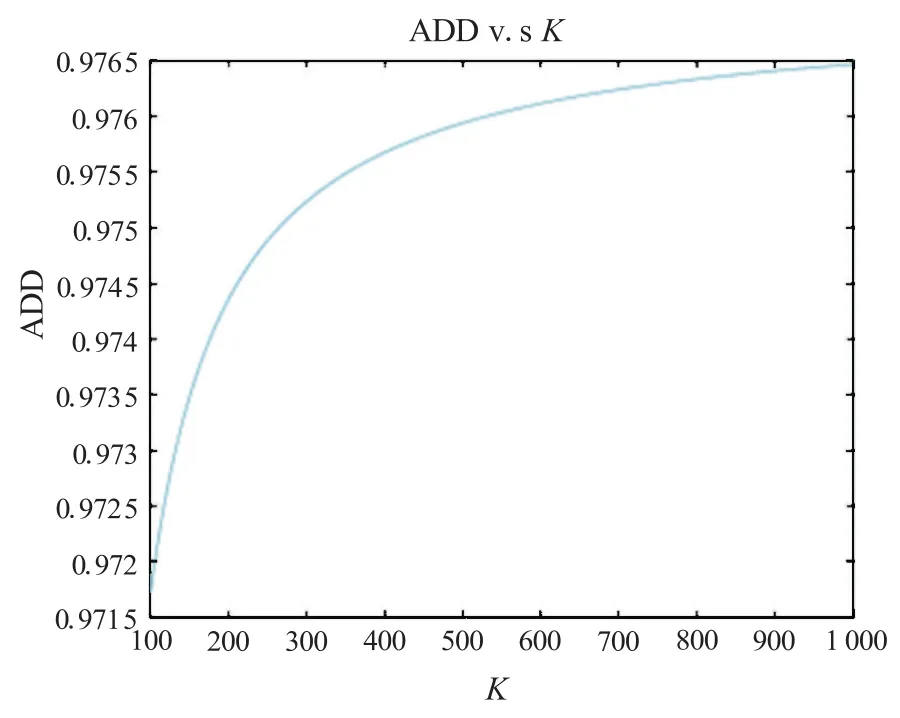
图2 ADD与银行数K的关系

σ*在[0，5]上取值，其他参数被固定为t=3,=1,c*=0.2,y*=-0.3,λ*=3,H=0.7,K=100 时，ADD与波动系数σ*的关系如图3。可以看出，随着波动系数σ*的增加，ADD随之递减，系统风险增加，并在达到一定值之后保持濒临违约状态。这是因为随着波动系数σ*的增加，系统环境变得越发不稳定，系统风险增加，当波动系数σ*达到一定值时，系统环境只是发生微小变化，系统就会有很强烈反应，随时可能违约。

图3 ADD与波动系数σ*的关系

4 小结

本文建立了一个由分数布朗运动驱动的银行间借贷模型，并证明了在特定的条件下模型存在唯一的非负强解。通过计算得到系统风险指标平均违约距离的数学表达式，并对该指标进行了数值模拟，对模拟结果进行了经济学解释。结论表明该模型具有较强的现实意义。