Sawad-Kotera方程的精确解

李 莉

(安徽农业大学 经济技术学院，安徽 合肥 230601)

孤子理论源于一些偏微分方程，其中Sawada-Kotera（SK）方程

是孤子理论中重要方程之一。SK方程包含着十分丰富的数学内容，如：Darboux变换[1]、双Hamiltonian 结构[2]、Backlund 变换和 Lax 表示[3-4]、尖孤立波解[5]、（2+1）维SK方程的精确孤立波解[6]和Y周期孤立波解的相互作用[7]。本人最近用Painlevé分析法得到了两个具有Painlevé可积性的超对称SK方程[8]。得到SK方程的更多数学内容，本文借鉴文献[9-11]的方法构造出SK方程的精确解，即从Laruent展式出发，用painlevé截断法构造出SK方程的几种特殊孤立子解。

1 Painlevé测试

假设在奇流行ϕ(x,t)=0附近，方程（1）的解为

为简化计算，下面用Kruskal的简化法，令

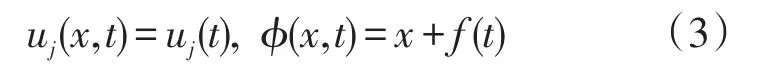
此外要求零阶系数不为零，即u0≠0。

首先，领头项分析。通过领头分析主要确定（2）式中的a,把u≈u0ϕ-α带入（1）中，得到α=2。

其次，共振点的确定。当（2）式中ϕj-2的系数uj(t)是任意函数时，就说在j处发生共振。把（2）和（3）式,以及a=2代入（1）得

当j=0时，由（4）可知u0=-6或u0=-12。

为寻求共振点，（4）式可写为P(j)uj=F(j)，其中，

从而，SK方程（1）式的共振点是方程P(j)=0的根。

当u0=-12时，P(j)=0的根为j=-2,-1,5,6,12，包含了两个负整数，此时（1）式不具有Painlevé性质；当u0=-6时方程P(j)=0的根为j=-1,2,3,6,10，其中j=-1对应着奇流行ϕ(x,t)的任意性，因此取u0=-6，舍去u0=-12。

最后，共振点的验证。用数学软件Maple14逐一验证上述共振点。把（2）式及a=2带入（1）式，整理ϕ(x,t)的各次幂系数并令其为零。

这是因为u2(x,t)是（1）式的共振点。

同样的方法可以将其它uj(x,t)都逐步定出来。因此，SK方程通过Painlevé测试。

2 SK方程的精确解

上一部分已经证明了SK具有Painlevé性质，本部分用截断的Painlevé展开式来寻求此方程更有意义的结果。

由上一部分知SK方程的Laurent展式为：

把（5）式和（9）式代入到（1）式中，整理ϕ-5,ϕ-4,ϕ-3,ϕ-2的系数，并令各系数为零，得到如下方程

令ϕ=ekx+ωt+ξ+A，则 可 由（9）～（12）式 求 出A=0,k任意,ω任意,ξ任意。

此时，ϕ=ekx+ωt+ξ，则u为常数,方程（1）只有常数解。

接下来，令uj=0,j≥2，则

把（5）、（6）和（13）带入（1）式，并整理ϕ-3,ϕ-2,ϕ-1的系数，并令各系数分别为零，有

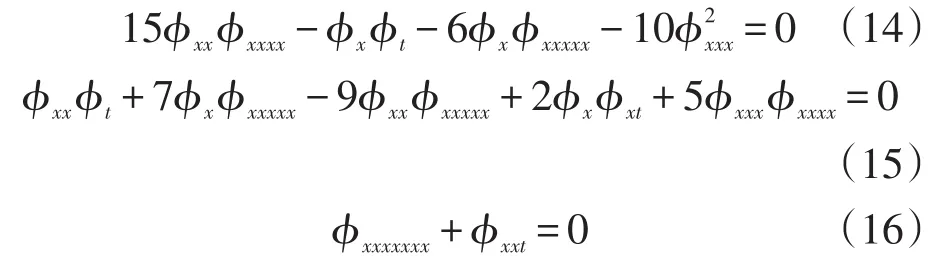
令ϕ=ekx+ωt+ξ+A，则由（14）～（16））式可得

第一种情况:k=0，而A,ω,ξ均是任意的。这与ϕx≠0矛盾，故舍去。

第二种情况:Α=0,而k,ω,ξ均是任意的。此时方程（1）的孤子解为u=0。

最后，令uj=0,j≥3，则

将（5）～（7）和（17）带 入（1）并 整 理ϕ-3,ϕ-2,ϕ-1,ϕ0，并令各阶系数分别为零，有

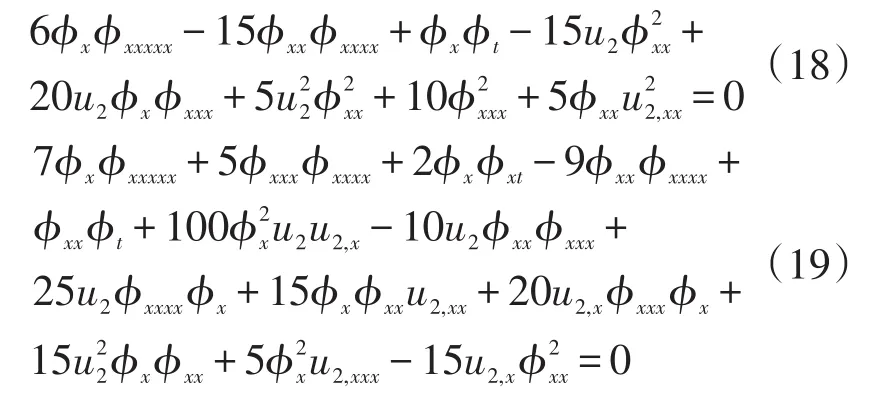
令ϕ=ekx+ωt+ξ+A，则可由 (19)～(21) 得k,ξ和A任意,，其中u2为任意常函数。此时方程(1)的孤子解为:

图1 SK方程的单孤子解的行波

3 小结

SK方程在通过Painlevé分析的前提下，对其进行Painlevé截断，不同的截断得到不同的精确解。最后得到一个具有稳定波形的孤子解。